use "https://stats.idre.ucla.edu/stat/stata/examples/greene/TBL5-1.DTA", clear rename x1 age rename x2 income rename x3 exp rename x4 ownrent rename x5 selfemp generate incomesq = income^2 drop if exp==0 save chapter12
Table 12.1, page 500. OLS.
regress exp age ownrent income incomesq
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 5.39
Model | 1749357.01 4 437339.252 Prob > F = 0.0008
Residual | 5432562.03 67 81083.0153 R-squared = 0.2436
-------------+------------------------------ Adj R-squared = 0.1984
Total | 7181919.03 71 101153.789 Root MSE = 284.75
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -3.081814 5.514717 -0.56 0.578 -14.08923 7.925606
ownrent | 27.94091 82.92232 0.34 0.737 -137.5727 193.4546
income | 234.347 80.36595 2.92 0.005 73.93593 394.7581
incomesq | -14.99684 7.469337 -2.01 0.049 -29.9057 -.0879859
_cons | -237.1465 199.3517 -1.19 0.238 -635.0541 160.7611
------------------------------------------------------------------------------
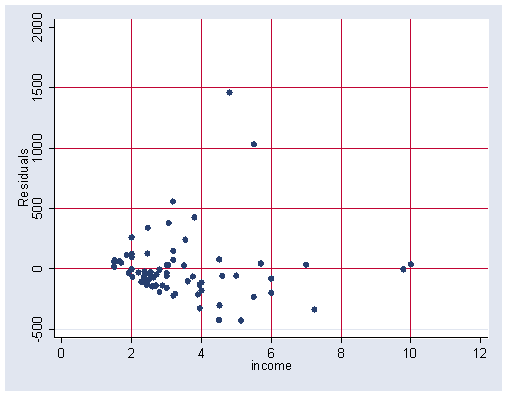
Figure 12.1, Residuals Against Income, page 500.
rvpplot income, xlabel(0(2)12) xline(2 4 6 8 10) ylabel(-500(500)2000) yline(0 500 1000 1500)
Table 12.2, Least squares, page 506. See results for Table 12.1 above.
Table 12.2, Davidson/MacKinnon(1), page 506.
regress exp age ownrent income incomesq, robust
Regression with robust standard errors Number of obs = 72
F( 4, 67) = 12.51
Prob > F = 0.0000
R-squared = 0.2436
Root MSE = 284.75
------------------------------------------------------------------------------
| Robust
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -3.081814 3.422641 -0.90 0.371 -9.913434 3.749805
ownrent | 27.94091 95.56573 0.29 0.771 -162.8091 218.6909
income | 234.347 92.12261 2.54 0.013 50.46954 418.2245
incomesq | -14.99684 7.199027 -2.08 0.041 -29.36616 -.6275259
_cons | -237.1465 220.795 -1.07 0.287 -677.8551 203.5621
------------------------------------------------------------------------------
Table 12.2, White, page 506. The White standard errors are just a rescaling of the Davidson/MacKinnon(1) standard errors by sqrt((N-k)/N). We will use some matrix commands to perform the computation.
matrix d = vecdiag(e(V))
matrix v = cholesky(diag(d))
matrix s = sqrt((72-5)/72)*vecdiag(v)
matrix list s
s[1,5]
age ownrent income incomesq _cons
r1 3.3016611 92.187776 88.866358 6.9445639 212.99053
Table 12.2, Davidson/MacKinnon(2), page 506.
regress exp age ownrent income incomesq, hc2
Regression with robust standard errors Number of obs = 72
F( 4, 67) = 12.06
Prob > F = 0.0000
R-squared = 0.2436
Root MSE = 284.75
------------------------------------------------------------------------------
| Robust HC2
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -3.081814 3.447715 -0.89 0.375 -9.963482 3.799853
ownrent | 27.94091 95.67211 0.29 0.771 -163.0214 218.9032
income | 234.347 92.08369 2.54 0.013 50.54722 418.1468
incomesq | -14.99684 7.199538 -2.08 0.041 -29.36718 -.6265067
_cons | -237.1465 221.0889 -1.07 0.287 -678.4419 204.1488
------------------------------------------------------------------------------
Example 12.5, page 510. Uses whitetst and bpagan commands by Christopher F. Baum and Nichols J. Cox. Use search whitetst to locate programs and download the program (see How can I use the search command to search for programs and get additional help? for more information about using search).
whitetst White's general test statistic : 14.32893 Chi-sq(12) P-value = .2802 bpagan income incomesq Breusch-Pagan LM statistic: 41.92031 Chi-sq( 2) P-value = 7.9e-10
Table 12.3, page 515 OLS. See results for Table 12.1 above.
Table 12.3, page 515. In the sections below we will show how to manually compute each of the results from Greene. It is also possible to compute these results using the wls0 command. You can download wls0 by typing search wls0 (see How can I use the search command to search for programs and get additional help? for more information about using search).
wls0 exp age ownrent income incomesq , wvar(income) type(abse) noconst /* 12.3a */ wls0 exp age ownrent income incomesq , wvar(incomesq) type(abse) noconst /* 12.3b */ wls0 exp age ownrent income incomesq , wvar(income incomesq) type(e2) noconst /* 12.3c */ wls0 exp age ownrent income incomesq , wvar(income incomesq) type(abse) noconst /* 12.3d */ wls0 exp age ownrent income incomesq , wvar(income incomesq) type(loge2) /* 12.3e */ wls0 exp age ownrent income incomesq , wvar(income incomesq) type(xb2) /* 12.3h */
Table 12.3a, page 515, Proportional to income.
regress exp age ownrent income incomesq [aw = 1/income]
(sum of wgt is 2.4956e+01)
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 5.73
Model | 1266234.79 4 316558.697 Prob > F = 0.0005
Residual | 3703808.18 67 55280.719 R-squared = 0.2548
-------------+------------------------------ Adj R-squared = 0.2103
Total | 4970042.96 71 70000.6051 Root MSE = 235.12
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -2.935011 4.603331 -0.64 0.526 -12.1233 6.253276
ownrent | 50.49364 69.87914 0.72 0.472 -88.9857 189.973
income | 202.1694 76.78152 2.63 0.010 48.91285 355.426
incomesq | -12.11364 8.27314 -1.46 0.148 -28.62689 4.39962
_cons | -181.8706 165.5191 -1.10 0.276 -512.2481 148.5068
------------------------------------------------------------------------------
Table 12.3b, page 515, Proportional to incomes.
regress exp age ownrent income incomesq [aw = 1/incomesq]
(sum of wgt is 9.9041e+00)
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 5.73
Model | 818838.837 4 204709.709 Prob > F = 0.0005
Residual | 2393372.15 67 35721.9724 R-squared = 0.2549
-------------+------------------------------ Adj R-squared = 0.2104
Total | 3212210.99 71 45242.4083 Root MSE = 189.00
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -2.694185 3.807306 -0.71 0.482 -10.2936 4.90523
ownrent | 60.44877 58.55089 1.03 0.306 -56.41929 177.3168
income | 158.427 76.39115 2.07 0.042 5.949597 310.9044
incomesq | -7.249289 9.724337 -0.75 0.459 -26.65915 12.16057
_cons | -114.1089 139.6875 -0.82 0.417 -392.9263 164.7085
------------------------------------------------------------------------------
Table 12.3c, page 515, Proportional to e^2.
regress exp age ownrent income incomesq
(output omitted)
predict e, resid
generate ee=e^2
regress ee income incomesq, noconst
(output omitted)
predict p1
regress exp age ownrent income incomesq [aw = 1/p1]
(sum of wgt is 8.8046e-04)
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 5.93
Model | 1454610.68 4 363652.671 Prob > F = 0.0004
Residual | 4111300.41 67 61362.6927 R-squared = 0.2613
-------------+------------------------------ Adj R-squared = 0.2172
Total | 5565911.10 71 78393.1141 Root MSE = 247.71
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -2.999273 4.842381 -0.62 0.538 -12.66471 6.666161
ownrent | 45.10975 73.42671 0.61 0.541 -101.4506 191.6701
income | 211.7943 73.52172 2.88 0.005 65.04438 358.5443
incomesq | -13.12857 7.233661 -1.81 0.074 -27.56702 1.309876
_cons | -196.0429 169.4295 -1.16 0.251 -534.2255 142.1398
------------------------------------------------------------------------------
Table 12.3d, page 515, Proportional to abs(e).
generate abse=abs(e)
regress abse income incomesq, noconst
(output omitted)
predict p2
regress exp age ownrent income incomesq [aw = 1/p2]
(sum of wgt is 4.3021e-01)
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 6.37
Model | 1626419.83 4 406604.957 Prob > F = 0.0002
Residual | 4277725.69 67 63846.6521 R-squared = 0.2755
-------------+------------------------------ Adj R-squared = 0.2322
Total | 5904145.52 71 83156.9792 Root MSE = 252.68
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -3.038906 4.953024 -0.61 0.542 -12.92518 6.84737
ownrent | 41.89772 75.32687 0.56 0.580 -108.4553 192.2508
income | 214.7859 70.17436 3.06 0.003 74.71733 354.8545
incomesq | -13.41379 6.353738 -2.11 0.038 -26.09591 -.7316792
_cons | -199.6993 170.1115 -1.17 0.245 -539.2433 139.8448
------------------------------------------------------------------------------
Table 12.3e, page 515, Proportional to log(e^2).
generate logee=log(ee)
regress logee income incomesq
(output omitted)
predict p3
replace p3 = exp(p3)
regress exp age ownrent income incomesq [aw = 1/p3]
(sum of wgt is 2.8166e-02)
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 69.69
Model | 2872576.04 4 718144.01 Prob > F = 0.0000
Residual | 690414.776 67 10304.6981 R-squared = 0.8062
-------------+------------------------------ Adj R-squared = 0.7947
Total | 3562990.82 71 50182.9693 Root MSE = 101.51
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -1.233683 2.551197 -0.48 0.630 -6.325894 3.858527
ownrent | 50.94976 52.81429 0.96 0.338 -54.468 156.3675
income | 145.3045 46.3627 3.13 0.003 52.76413 237.8448
incomesq | -7.93828 3.736716 -2.12 0.037 -15.3968 -.4797647
_cons | -117.8675 101.3862 -1.16 0.249 -320.2352 84.50027
------------------------------------------------------------------------------
Table 12.3f, page 515, First step of two-step estimation.
generate loginc = log(income)
regress logee loginc
(output omitted)
predict p4
replace p4 = exp(p4)
regress exp age ownrent income incomesq [aw=1/p4]
(sum of wgt is 8.5730e-03)
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 5.69
Model | 1356781.78 4 339195.444 Prob > F = 0.0005
Residual | 3991163.63 67 59569.6064 R-squared = 0.2537
-------------+------------------------------ Adj R-squared = 0.2091
Total | 5347945.41 71 75323.1747 Root MSE = 244.07
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -2.957872 4.762688 -0.62 0.537 -12.46424 6.548494
ownrent | 47.35701 72.13892 0.66 0.514 -96.63288 191.3469
income | 208.8759 77.19801 2.71 0.009 54.78803 362.9638
incomesq | -12.7688 8.083831 -1.58 0.119 -28.90419 3.366592
_cons | -193.3253 171.0833 -1.13 0.263 -534.8089 148.1583
------------------------------------------------------------------------------
Table 12.3g, page 515, ML. Uses the reghv command by Jeroen Weesie. Use search reghv to find program and download the program (see How can I use the search command to search for programs and get additional help? for more information about using search).
reghv exp age ownrent income incomesq, var(loginc)
Multiplicative heteroscedastic regression Number of obs = 72
Estimator: mle Model chi2(5) = 68.428
Prob > chi2 = 0.000
Log Likelihood = -482.324 Pseudo R2 = 0.0662
VWLS R2 = 0.2421
------------------------------------------------------------------------------
exp | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lp_mean |
age | -1.705189 2.758016 -0.62 0.536 -7.110802 3.700424
ownrent | 58.09752 43.5065 1.34 0.182 -27.17365 143.3687
income | 75.93179 81.04202 0.94 0.349 -82.90765 234.7712
incomesq | 4.397655 13.43429 0.33 0.743 -21.93306 30.72838
_cons | -19.21409 113.0557 -0.17 0.865 -240.7992 202.371
-------------+----------------------------------------------------------------
lp_lnvar |
loginc | 3.651688 .3987368 9.16 0.000 2.870178 4.433198
_cons | 6.397951 .4840636 13.22 0.000 5.449203 7.346698
------------------------------------------------------------------------------
Table 12.3h, page 515, Proportional to (xb)^2.
regress exp age ownrent income incomesq
(output omitted)
predict p
generate p5 = p^2
regress exp age ownrent income incomesq [aw=1/p5]
(sum of wgt is 2.3408e-02)
Source | SS df MS Number of obs = 72
-------------+------------------------------ F( 4, 67) = 8.54
Model | 102540.932 4 25635.2329 Prob > F = 0.0000
Residual | 201093.219 67 3001.39133 R-squared = 0.3377
-------------+------------------------------ Adj R-squared = 0.2982
Total | 303634.151 71 4276.53734 Root MSE = 54.785
------------------------------------------------------------------------------
exp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .7315878 1.43144 0.51 0.611 -2.125579 3.588755
ownrent | -.2846994 46.67003 -0.01 0.995 -93.43847 92.86907
income | 136.8154 48.40296 2.83 0.006 40.20271 233.4281
incomesq | -6.207781 6.76926 -0.92 0.362 -19.71928 7.303718
_cons | -148.1926 64.74939 -2.29 0.025 -277.4329 -18.95225
------------------------------------------------------------------------------
Table 12.4, page 521, Maximum Likelihood Estimates. We will again use the reghv command shown above in Table 12.3g.
reghv exp age ownrent income incomesq, var(income incomesq)
Multiplicative heteroscedastic regression Number of obs = 72
Estimator: mle Model chi2(6) = 101.113
Prob > chi2 = 0.000
Log Likelihood = -465.982 Pseudo R2 = 0.0979
VWLS R2 = 0.9584
------------------------------------------------------------------------------
exp | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lp_mean |
age | -.3759981 .550001 -0.68 0.494 -1.45398 .701984
ownrent | 33.3591 37.13479 0.90 0.369 -39.42375 106.142
income | 96.82688 31.79803 3.05 0.002 34.50389 159.1499
incomesq | -3.801144 2.624785 -1.45 0.148 -8.945629 1.343341
_cons | -58.44412 62.09841 -0.94 0.347 -180.1548 63.26654
-------------+----------------------------------------------------------------
lp_lnvar |
income | 5.35449 .3750446 14.28 0.000 4.619416 6.089564
incomesq | -.5631181 .036122 -15.59 0.000 -.6339159 -.4923202
_cons | -.0415783 .8079218 -0.05 0.959 -1.625076 1.541919
------------------------------------------------------------------------------