use "https://stats.idre.ucla.edu/stat/stata/examples/greene/TBL19-1.DTA", clear
Example 19.1 on page 816. The column for linear regression of Table 19.1 is obtained using a least square regression model.
regress grade gpa tuce psi
Source | SS df MS Number of obs = 32
-------------+------------------------------ F( 3, 28) = 6.65
Model | 3.00227631 3 1.00075877 Prob > F = 0.0016
Residual | 4.21647369 28 .150588346 R-squared = 0.4159
-------------+------------------------------ Adj R-squared = 0.3533
Total | 7.21875 31 .232862903 Root MSE = .38806
------------------------------------------------------------------------------
grade | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | .4638517 .1619563 2.86 0.008 .1320992 .7956043
tuce | .0104951 .0194829 0.54 0.594 -.0294137 .0504039
psi | .3785548 .1391727 2.72 0.011 .0934724 .6636372
_cons | -1.498017 .5238886 -2.86 0.008 -2.571154 -.4248801
------------------------------------------------------------------------------
The slope for each parameter in the case of linear regression is simply the parameter itself since it is linear. The density function is simply the constant 1 for linear regression. The column for logistic regression of Table 19.1 is obtained using a logistic regression model.
logit grade gpa tuce psi
(Intermediate results omitted)
Logit estimates Number of obs = 32
LR chi2(3) = 15.40
Prob > chi2 = 0.0015
Log likelihood = -12.889633 Pseudo R2 = 0.3740
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 2.826113 1.262941 2.24 0.025 .3507938 5.301432
tuce | .0951577 .1415542 0.67 0.501 -.1822835 .3725988
psi | 2.378688 1.064564 2.23 0.025 .29218 4.465195
_cons | -13.02135 4.931325 -2.64 0.008 -22.68657 -3.35613
------------------------------------------------------------------------------
In Stata 7, we use the mfx command to get the marginal effect with option nodiscrete so the variable psi is treated as a continuous variable.
mfx compute, nodiscrete
Marginal effects after logit
y = Pr(grade) (predict)
= .25282025
------------------------------------------------------------------------------
variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X
---------+--------------------------------------------------------------------
gpa | .5338589 .23704 2.25 0.024 .069273 .998445 3.11719
tuce | .0179755 .02624 0.69 0.493 -.033448 .069399 21.9375
psi | .4493393 .19676 2.28 0.022 .063691 .834987 .437500
------------------------------------------------------------------------------
We now calculate the scale factor of the last row in the table for logistic regression. Matrix x stores the coefficient estimates and matrix m stores the mean vector for the independent variables including the constant term.
matrix x=e(b)
matrix accum a=gpa tuce psi, mean(m)
(obs=32)
matrix list m
m[1,4]
gpa tuce psi _cons
_cons 3.1171875 21.9375 .4375 1
matrix c=x*m'
matrix list c
symmetric c[1,1]
_cons
y1 -1.083627
Now we use the density function for the logistic distribution (19-11) on page 815 to get the scale factor below.
di exp(trace(c))/(1+exp(trace(c)))^2 .18890217
The column for probit regression of Table 19.1 is obtained using a probit model.
probit grade gpa tuce psi
(Intermediate results omitted)
Probit estimates Number of obs = 32
LR chi2(3) = 15.55
Prob > chi2 = 0.0014
Log likelihood = -12.818803 Pseudo R2 = 0.3775
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 1.62581 .6938818 2.34 0.019 .2658269 2.985794
tuce | .0517289 .0838901 0.62 0.537 -.1126927 .2161506
psi | 1.426332 .595037 2.40 0.017 .2600814 2.592583
_cons | -7.45232 2.542467 -2.93 0.003 -12.43546 -2.469177
------------------------------------------------------------------------------
In the same way as in logistic regression, we can to get the marginal effect using mfx and treat psi as a continuous variable.
mfx compute, nodiscrete
Marginal effects after probit
y = Pr(grade) (predict)
= .26580809
------------------------------------------------------------------------------
variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X
---------+--------------------------------------------------------------------
gpa | .5333471 .23246 2.29 0.022 .077726 .988968 3.11719
tuce | .0169697 .02712 0.63 0.531 -.036184 .070123 21.9375
psi | .4679084 .18764 2.49 0.013 .100136 .83568 .437500
------------------------------------------------------------------------------
Similar to the case of logistic regression, we can get the scale factor by the following calculation.
matrix x=e(b) matrix accum a=gpa tuce psi, mean(m) (obs=32) matrix c=x*m'
Now we use the standard normal distribution for the probit model to get the scale factor.
di normalden(trace(c)) .32805002
Last column of Table 19.1 is obtained using a little bit more maximum likelihood programming in Stata.
gen d0 = 1-grade
gen d1 = grade
capture program drop myweib
program define myweib
version 6
args lnf theta
quietly replace `lnf'=-d0*exp(`theta')+d1*log(1-exp(-exp(`theta')))
end
ml model lf myweib (grade=gpa tuce psi)
ml maximize
initial: log likelihood = -26.045427
alternative: log likelihood = -21.404965
rescale: log likelihood = -20.686846
Iteration 0: log likelihood = -20.686846
Iteration 1: log likelihood = -16.296453
Iteration 2: log likelihood = -13.074668
Iteration 3: log likelihood = -13.008153
Iteration 4: log likelihood = -13.008003
Iteration 5: log likelihood = -13.008003
Number of obs = 32
Wald chi2(3) = 10.19
Log likelihood = -13.008003 Prob > chi2 = 0.0170
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 2.293553 1.035001 2.22 0.027 .2649881 4.322118
tuce | .041156 .1073136 0.38 0.701 -.1691748 .2514867
psi | 1.562276 .7305064 2.14 0.032 .1305096 2.994042
_cons | -10.03142 3.479058 -2.88 0.004 -16.85025 -3.212591
------------------------------------------------------------------------------
Now let’s calculate the slope at mean, this is the last column in Table 19.1 Using the model specified in Example 19.1, we can derive the derivative and plug in the mean vector. Matrix x stores the coefficient estimates and matrix m stores the mean vector of independent variables including the constant term. Finally vector y stores the slope for each independent variable at its mean value. The last display shows the scale factor computed at the means of the variables.
matrix x=e(b)
matrix accum a=gpa tuce psi, mean(m)
(obs=32)
matrix c=x*m'
matrix list c
symmetric c[1,1]
_cons
y1 -1.2956303
local d = exp(-exp(trace(c)))*exp(trace(c))
matrix y=`d'*x
matrix list y
y[1,4]
eq1: eq1: eq1: eq1:
gpa tuce psi _cons
y1 .47747024 .00856782 .3252335 -2.0883339
di exp(-exp(trace(c)))*exp(trace(c))
20817929
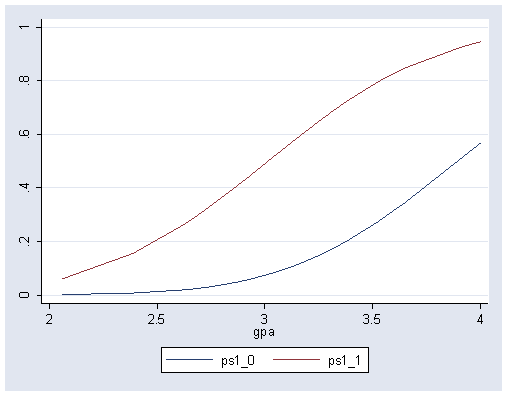
Example 19.2 on page 817.
gen ps1_0=norm(-7.45+1.62*gpa+.052*21.938) gen ps1_1=norm(-7.45+1.62*gpa+.052*21.938+1.4263) sort gpa graph twoway scatter ps1_0 ps1_1 gpa if gpa>=2, msymbol(i i) connect(l l)
Example 19.4 and Table 19.2 on page 825.
logit grade gpa tuce psi
(Intermediate results omitted)
Logit estimates Number of obs = 32
LR chi2(3) = 15.40
Prob > chi2 = 0.0015
Log likelihood = -12.889633 Pseudo R2 = 0.3740
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 2.826113 1.262941 2.24 0.025 .3507938 5.301432
tuce | .0951577 .1415542 0.67 0.501 -.1822835 .3725988
psi | 2.378688 1.064564 2.23 0.025 .29218 4.465195
_cons | -13.02135 4.931325 -2.64 0.008 -22.68657 -3.35613
------------------------------------------------------------------------------
mfx compute, nodiscrete
Marginal effects after logit
y = Pr(grade) (predict)
= .25282025
------------------------------------------------------------------------------
variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X
---------+--------------------------------------------------------------------
gpa | .5338589 .23704 2.25 0.024 .069273 .998445 3.11719
tuce | .0179755 .02624 0.69 0.493 -.033448 .069399 21.9375
psi | .4493393 .19676 2.28 0.022 .063691 .834987 .437500
------------------------------------------------------------------------------
probit grade gpa tuce psi
(Intermediate results omitted)
Probit estimates Number of obs = 32
LR chi2(3) = 15.55
Prob > chi2 = 0.0014
Log likelihood = -12.818803 Pseudo R2 = 0.3775
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 1.62581 .6938818 2.34 0.019 .2658269 2.985794
tuce | .0517289 .0838901 0.62 0.537 -.1126927 .2161506
psi | 1.426332 .595037 2.40 0.017 .2600814 2.592583
_cons | -7.45232 2.542467 -2.93 0.003 -12.43546 -2.469177
------------------------------------------------------------------------------
mfx compute, nodiscrete
Marginal effects after probit
y = Pr(grade) (predict)
= .26580809
------------------------------------------------------------------------------
variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X
---------+--------------------------------------------------------------------
gpa | .5333471 .23246 2.29 0.022 .077726 .988968 3.11719
tuce | .0169697 .02712 0.63 0.531 -.036184 .070123 21.9375
psi | .4679084 .18764 2.49 0.013 .100136 .83568 .437500
------------------------------------------------------------------------------
Example 19.6 on page 826. The right-hand corner of the first output below gives the chi-square value and p-value for the probit model. The right-hand corner of the second output below gives the chi-square and p-value for the logit model.
probit grade gpa tuce psi
(Intermediate results omitted)
Probit estimates Number of obs = 32
LR chi2(3) = 15.55
Prob > chi2 = 0.0014
Log likelihood = -12.818803 Pseudo R2 = 0.3775
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 1.62581 .6938818 2.34 0.019 .2658269 2.985794
tuce | .0517289 .0838901 0.62 0.537 -.1126927 .2161506
psi | 1.426332 .595037 2.40 0.017 .2600814 2.592583
_cons | -7.45232 2.542467 -2.93 0.003 -12.43546 -2.469177
------------------------------------------------------------------------------
logit grade gpa tuce psi
(Intermediate results omitted)
Logit estimates Number of obs = 32
LR chi2(3) = 15.40
Prob > chi2 = 0.0015
Log likelihood = -12.889633 Pseudo R2 = 0.3740
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 2.826113 1.262941 2.24 0.025 .3507938 5.301432
tuce | .0951577 .1415542 0.67 0.501 -.1822835 .3725988
psi | 2.378688 1.064564 2.23 0.025 .29218 4.465195
_cons | -13.02135 4.931325 -2.64 0.008 -22.68657 -3.35613
------------------------------------------------------------------------------
Now let’s do the second part of the example. We first run the full model and then run separate models for the case when psi==0 and when psi==1. We store the log likelihood in a local variable for each model and compare them afterwards.
probit grade gpa tuce
(Intermediate results omitted)
Probit estimates Number of obs = 32
LR chi2(2) = 8.88
Prob > chi2 = 0.0118
Log likelihood = -16.152157 Pseudo R2 = 0.2156
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 1.409575 .6354662 2.22 0.027 .1640846 2.655066
tuce | .0526675 .0755527 0.70 0.486 -.0954132 .2007481
_cons | -6.034327 2.121027 -2.85 0.004 -10.19146 -1.877191
------------------------------------------------------------------------------
local l10 = e(ll)
probit grade gpa tuce if psi==0
(Intermediate results omitted)
Probit estimates Number of obs = 18
LR chi2(2) = 8.90
Prob > chi2 = 0.0117
Log likelihood = -3.6612274 Pseudo R2 = 0.5486
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 3.092025 1.813587 1.70 0.088 -.4625411 6.646591
tuce | .1535286 .2708777 0.57 0.571 -.377382 .6844391
_cons | -14.90758 9.85688 -1.51 0.130 -34.22671 4.411545
------------------------------------------------------------------------------
local l0=e(ll)
probit grade gpa tuce if psi==1
(Intermediate results omitted)
Probit estimates Number of obs = 14
LR chi2(2) = 2.69
Prob > chi2 = 0.2609
Log likelihood = -8.217242 Pseudo R2 = 0.1405
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 1.102962 .7846481 1.41 0.160 -.4349205 2.640844
tuce | .0276161 .0984905 0.28 0.779 -.1654217 .2206539
_cons | -3.870036 2.861729 -1.35 0.176 -9.478921 1.738849
------------------------------------------------------------------------------
local l1=e(ll)
di 2*(`l1'+`l0'-`l10')
8.5473743
di chi2tail(3, 8.54743)
03595439
We can also get the critical value for 95%.
di invchi2tail(3, .05) 7.8147278
Example 19.7 and Table 19.3 on page 830. The first estimate is obtained by running a probit model and the second one is obtained by running heteroscedastic probit model.
probit grade gpa tuce psi
(Intermediate results omitted)
Probit estimates Number of obs = 32
LR chi2(3) = 15.55
Prob > chi2 = 0.0014
Log likelihood = -12.818803 Pseudo R2 = 0.3775
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gpa | 1.62581 .6938818 2.34 0.019 .2658269 2.985794
tuce | .0517289 .0838901 0.62 0.537 -.1126927 .2161506
psi | 1.426332 .595037 2.40 0.017 .2600814 2.592583
_cons | -7.45232 2.542467 -2.93 0.003 -12.43546 -2.469177
------------------------------------------------------------------------------
hetprob grade gpa tuce psi, het( psi)
Fitting comparison model:
Iteration 0: log likelihood = -20.59173
Iteration 1: log likelihood = -13.315851
Iteration 2: log likelihood = -12.832843
Iteration 3: log likelihood = -12.818826
Iteration 4: log likelihood = -12.818803
Fitting full model:
Iteration 0: log likelihood = -12.818803
Iteration 1: log likelihood = -12.080094
Iteration 2: log likelihood = -11.965838
Iteration 3: log likelihood = -11.896545
Iteration 4: log likelihood = -11.895852
Iteration 5: log likelihood = -11.895851
Heteroskedastic probit model Number of obs = 32
Zero outcomes = 21
Nonzero outcomes = 11
Wald chi2(3) = 3.33
Log likelihood = -11.89585 Prob > chi2 = 0.3438
------------------------------------------------------------------------------
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
grade |
gpa | 3.12155 1.760869 1.77 0.076 -.3296887 6.572789
tuce | .1237515 .2134227 0.58 0.562 -.2945493 .5420523
psi | 2.34322 1.670631 1.40 0.161 -.9311565 5.617597
_cons | -14.28904 8.860899 -1.61 0.107 -31.65609 3.077997
-------------+----------------------------------------------------------------
lnsigma2 |
psi | 1.093371 .8805796 1.24 0.214 -.6325333 2.819275
------------------------------------------------------------------------------
Likelihood ratio test of lnsigma2=0: chi2(1) = 1.85 Prob > chi2 = 0.1743
The first LR test comes as a part of the output from the hetprob procedure as shown above. Stata does not have a LM test yet. For Wald test, we can simply calculate it manually as shown in the book. Stata’s hetprobit has an option that does robust standard error estimate and Wald test for it as shown after our manual computation of Wald test.
di (1.09337/.8805795)^2
1.5416904
hetprob grade gpa tuce psi, het( psi) robust nolog
Heteroskedastic probit model Number of obs = 32
Zero outcomes = 21
Nonzero outcomes = 11
Wald chi2(3) = 9.51
Log likelihood = -11.89585 Prob > chi2 = 0.0232
------------------------------------------------------------------------------
| Robust
grade | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
grade |
gpa | 3.121551 1.129778 2.76 0.006 .9072259 5.335875
tuce | .1237516 .1428788 0.87 0.386 -.1562857 .4037888
psi | 2.343221 1.502745 1.56 0.119 -.6021045 5.288546
_cons | -14.28905 4.881214 -2.93 0.003 -23.85605 -4.722045
-------------+----------------------------------------------------------------
lnsigma2 |
psi | 1.093371 .7252922 1.51 0.132 -.3281753 2.514918
------------------------------------------------------------------------------
Wald test of lnsigma2=0: chi2(1) = 2.27 Prob > chi2 = 0.1317
Example 19.18 on page 868 on nested logit. The independent variables are ttme — terminal time (zero for car), hinc — household income and gc — generalized cost. The dependent variable is mode–the choice that a person makes among four travel modes. The data set is in such a format that each person has as many observations as the number of choices. For instance, in our case, each person has four choices and there are 210 people in the dataset. Therefore, the total number of observations in this dataset is 210*4 = 840. In other words, each four observations in the dataset correspond to a choice that a person makes. In order to run the nested logit analysis in Stata 7, we need to create a couple of variables needed to build up the nested logit tree. First, we need a group variable that corresponds to a person. In our case, every four observations will be a group. This is done by using command generate with group function. Secondly we need a variable that corresponds to all the possible choices. To this end, we generate a variable called travel based on the group variable.
use "https://stats.idre.ucla.edu/stat/stata/examples/greene/TBL19-2.DTA", clear
gen grp = group(210)
sort grp
by grp: gen travel=_n-1
list in 1/10
mode ttme invc invt gc hinc psize grp travel
1. 0 69 59 100 70 35 1 1 0
2. 0 34 31 372 71 35 1 1 1
3. 0 35 25 417 70 35 1 1 2
4. 1 0 10 180 30 35 1 1 3
5. 0 64 58 68 68 30 2 2 0
6. 0 44 31 354 84 30 2 2 1
7. 0 53 25 399 85 30 2 2 2
8. 1 0 11 255 50 30 2 2 3
9. 0 69 115 125 129 40 1 3 0
10. 0 34 98 892 195 40 1 3 1
label define tlab 0 "air" 1 "train" 2 "bus" 3 "car"
label value travel tlab
tab travel
travel | Freq. Percent Cum.
------------+-----------------------------------
air | 210 25.00 25.00
train | 210 25.00 50.00
bus | 210 25.00 75.00
car | 210 25.00 100.00
------------+-----------------------------------
Total | 840 100.00
nlogitgen type = travel(fly: 0, ground: 1 | 2 | 3)
new variable type is generated with 2 groups
lb_type:
1 fly
2 ground
nlogittree travel type
tree structure specified for the nested logit model
top-->bottom
type travel
------------------------
fly air
ground train
bus
car
We have successfully built the nested logit tree now. We need more dummy variables for the choices and interaction of choices with household income. We create them below.
gen aasc = mod(_n, 4)==1 gen tasc = mod(_n, 4)==2 gen basc = mod(_n, 4)==3 gen casc = mod(_n, 4)==0 gen hincair = hinc*aasc
The following model corresponds to Table 19.12 on page 869, the unconditional estimate. Since the model is not nested, it gives the exact output as clogit shown below. In this case, we should use clogit since it is much faster.
nlogit mode (travel = aasc tasc basc gc ttme hincair), group(grp)
note: nonnested model, results are the same as -clogit-
initial: log likelihood = -199.12837
rescale: log likelihood = -199.12837
Iteration 0: log likelihood = -199.12837
Iteration 1: log likelihood = -199.12837
Nested logit
Levels = 1 Number of obs = 840
Dependent variable = mode LR chi2(6) = 183.9869
Log likelihood = -199.12837 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
travel |
aasc | 5.207443 .7790551 6.68 0.000 3.680523 6.734363
tasc | 3.869043 .4431269 8.73 0.000 3.00053 4.737555
basc | 3.163194 .4502659 7.03 0.000 2.280689 4.045699
gc | -.0155015 .004408 -3.52 0.000 -.024141 -.006862
ttme | -.0961248 .0104398 -9.21 0.000 -.1165865 -.0756631
hincair | .013287 .0102624 1.29 0.195 -.0068269 .033401
-------------+----------------------------------------------------------------
(IV params) |
|
(none) |
------------------------------------------------------------------------------
LR test of homoskedasticity (iv = 1): chi2(0)= 0.00 Prob > chi2 = .
------------------------------------------------------------------------------
clogit mode aasc tasc basc gc ttme hincair, group(grp)
Iteration 0: log likelihood = -262.32267
Iteration 1: log likelihood = -203.53119
Iteration 2: log likelihood = -199.2783
Iteration 3: log likelihood = -199.12868
Iteration 4: log likelihood = -199.12837
Conditional (fixed-effects) logistic regression Number of obs = 840
LR chi2(6) = 183.99
Prob > chi2 = 0.0000
Log likelihood = -199.12837 Pseudo R2 = 0.3160
------------------------------------------------------------------------------
mode | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
aasc | 5.207443 .7790525 6.68 0.000 3.680528 6.734358
tasc | 3.869043 .4431252 8.73 0.000 3.000533 4.737552
basc | 3.163194 .4502646 7.03 0.000 2.280692 4.045697
gc | -.0155015 .004408 -3.52 0.000 -.024141 -.006862
ttme | -.0961248 .0104398 -9.21 0.000 -.1165864 -.0756632
hincair | .013287 .0102624 1.29 0.195 -.0068269 .0334009
------------------------------------------------------------------------------
The following model corresponds to Table 19.12 on page 869, the FIML estimate.
nlogit mode (travel = aasc tasc basc gc ttme) (type=hincair), group(grp)
tree structure specified for the nested logit model
top-->bottom
type travel
------------------------
fly air
ground train
bus
car
initial: log likelihood = -207.01917
rescale: log likelihood = -207.01917
rescale eq: log likelihood = -197.65917
Iteration 0: log likelihood = -197.65917
Iteration 1: log likelihood = -197.43396 (backed up)
Iteration 2: log likelihood = -197.18788 (backed up)
Iteration 3: log likelihood = -197.17125 (backed up)
Iteration 4: log likelihood = -197.08544 (backed up)
Iteration 5: log likelihood = -196.84835
Iteration 6: log likelihood = -196.30583
Iteration 7: log likelihood = -194.93294
Iteration 8: log likelihood = -194.86168
Iteration 9: log likelihood = -194.0501
Iteration 10: log likelihood = -193.91879
Iteration 11: log likelihood = -193.75031
Iteration 12: log likelihood = -193.68313
Iteration 13: log likelihood = -193.66092
Iteration 14: log likelihood = -193.65718
Iteration 15: log likelihood = -193.6562
Iteration 16: log likelihood = -193.65615
Iteration 17: log likelihood = -193.65615
Nested logit
Levels = 2 Number of obs = 840
Dependent variable = mode LR chi2(8) = 194.9313
Log likelihood = -193.65615 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
travel |
aasc | 6.042255 1.198907 5.04 0.000 3.692441 8.39207
tasc | 5.064679 .6620317 7.65 0.000 3.767121 6.362237
basc | 4.096302 .6151582 6.66 0.000 2.890614 5.30199
gc | -.0315888 .0081566 -3.87 0.000 -.0475754 -.0156022
ttme | -.1126183 .0141293 -7.97 0.000 -.1403111 -.0849254
-------------+----------------------------------------------------------------
type |
hincair | .0153337 .0093814 1.63 0.102 -.0030534 .0337209
-------------+----------------------------------------------------------------
(IV params) |
|
type |
/fly | .5859993 .1406199 4.17 0.000 .3103894 .8616092
/ground | .3889488 .1236623 3.15 0.002 .1465753 .6313224
------------------------------------------------------------------------------
LR test of homoskedasticity (iv = 1): chi2(2)= 10.94 Prob > chi2 = 0.0042
------------------------------------------------------------------------------
The following is an attempt to create a LIML (limited information maximum likelihood) model corresponds to table 19.12, the LIML estimate. This is a two-step procedure. Stata currently does not support LIML yet. So we have to do some extra work here. The first step is to estimate the choice model for the three choices in the ground branch. Using variable type that we created before for nested logit tree, we create a new variable called method to indicate the branches. We then use clogit making use of the group structure.
tab type, gen(method)
type | Freq. Percent Cum.
------------+-----------------------------------
fly | 210 25.00 25.00
ground | 630 75.00 100.00
------------+-----------------------------------
Total | 840 100.00
clogit mode tasc basc gc ttme if method2==1, group(grp)
note: 58 groups (174 obs) dropped due to all positive or
all negative outcomes.
Iteration 0: log likelihood = -151.84818
Iteration 1: log likelihood = -93.828969
Iteration 2: log likelihood = -88.408188
Iteration 3: log likelihood = -87.943715
Iteration 4: log likelihood = -87.938161
Iteration 5: log likelihood = -87.93816
Conditional (fixed-effects) logistic regression Number of obs = 456
LR chi2(4) = 158.10
Prob > chi2 = 0.0000
Log likelihood = -87.93816 Pseudo R2 = 0.4734
------------------------------------------------------------------------------
mode | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
tasc | 4.463668 .6405338 6.97 0.000 3.208245 5.719091
basc | 3.104744 .6090192 5.10 0.000 1.911088 4.2984
gc | -.0636819 .0100424 -6.34 0.000 -.0833646 -.0439992
ttme | -.0698778 .0148803 -4.70 0.000 -.0990427 -.040713
------------------------------------------------------------------------------
So we have seen that we have correctly estimated the coefficient for variables tasc, basc, gc and ttme. We now try to compute the inclusive values using the formula at the bottom of page 866.
matrix X=e(b) matrix V1=e(V) gen myivb=X[1,1]*tasc + X[1,2]*basc + X[1,3]*gc + X[1,4]*ttme replace myivb = log(exp(myivb)+exp(myivb[_n+1])+exp(myivb[_n+2])) if mod(_n,4)==2 (210 real changes made) replace myivb = myivb[_n-1] if mod(_n,4)==3 | mod(_n, 4)==0 (420 real changes made) gen ivair=aasc*myivb gen ivground=(1-aasc)*myivb
So far, we have the variables IV_fly and IV_ground computed correctly. Next step is to compute the last model. Since we now look at a higher level we need to reshape our dataset. We only have two choices, ground versus fly. The variable branch is created corresponding to the two choices. We then have to drop half of the observations since we only have two choices for each person instead of four. clogit is used again to obtain the parameter estimate for branch level variables. You can see that the coefficient estimates are correct but not the standard error. This is because LIML uses different method of estimating the standard errors which involves some matrix computation.
preserve
gen branch=mode*type
replace branch = branch[_n+1] | branch[_n+2] | branch[_n] if mod(_n, 4)==2
(152 real changes made)
drop if mod(_n, 4)==3 | mod(_n, 4)==0
(420 observations deleted)
drop grp
gen grp=group(210)
clogit branch aasc hincair ivair ivground, group(grp)
Iteration 0: log likelihood = -127.30482
Iteration 1: log likelihood = -115.71699
Iteration 2: log likelihood = -115.33683
Iteration 3: log likelihood = -115.33543
Iteration 4: log likelihood = -115.33543
Conditional (fixed-effects) logistic regression Number of obs = 420
LR chi2(4) = 60.45
Prob > chi2 = 0.0000
Log likelihood = -115.33543 Pseudo R2 = 0.2076
------------------------------------------------------------------------------
branch | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
aasc | -.0647031 .9836824 -0.07 0.948 -1.992685 1.863279
hincair | .0207877 .0085162 2.44 0.015 .0040962 .0374791
ivair | .2266246 .1005949 2.25 0.024 .0294622 .4237869
ivground | .158721 .0717853 2.21 0.027 .0180245 .2994175
------------------------------------------------------------------------------
restore
Example 19.22 on Poisson regression. We’ll skip here the measure of goodness-of-fit based on the standardized residuals and the measure based on the deviance.
use "https://stats.idre.ucla.edu/stat/stata/examples/greene/TBL19-3.DTA", clear
gen logm=log(months)
(6 missing values generated)
constraint define 1 logm=1
poisson acc tb tc td te t6569 t7074 t7579 o7579 logm, const(1)
Iteration 0: log likelihood = -119.39808
Iteration 1: log likelihood = -81.620956
Iteration 2: log likelihood = -68.436229
Iteration 3: log likelihood = -68.414556
Iteration 4: log likelihood = -68.414554
Poisson regression Number of obs = 34
LR chi2(9) = 575.58
Prob > chi2 = 0.0000
Log likelihood = -68.414554 Pseudo R2 = 0.8079
------------------------------------------------------------------------------
acc | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
tb | -.5447114 .1776135 -3.07 0.002 -.8928274 -.1965954
tc | -.6887643 .3290358 -2.09 0.036 -1.333663 -.043866
td | -.0743091 .2905578 -0.26 0.798 -.6437919 .4951737
te | .320529 .235752 1.36 0.174 -.1415365 .7825945
t6569 | .6958455 .1496562 4.65 0.000 .4025246 .9891663
t7074 | .8174555 .1698376 4.81 0.000 .4845798 1.150331
t7579 | .4449709 .2332392 1.91 0.056 -.0121695 .9021113
o7579 | .3838589 .1182605 3.25 0.001 .1520726 .6156451
logm | 1 . . . . .
_cons | -6.402877 .2175228 -29.44 0.000 -6.829214 -5.97654
------------------------------------------------------------------------------
lrtest, saving(0)
* Stata 8 code.
poisgof
* Stata 9 code and output.
estat gof
Goodness-of-fit chi2 = 38.96253
Prob > chi2(24) = 0.0276
poisson acc t6569 t7074 t7579 o7579 logm, const(1)
Iteration 0: log likelihood = -1166.5368
Iteration 1: log likelihood = -89.701554
Iteration 2: log likelihood = -80.215736
Iteration 3: log likelihood = -80.201227
Iteration 4: log likelihood = -80.201226
Poisson regression Number of obs = 34
LR chi2(5) = 552.00
Prob > chi2 = 0.0000
Log likelihood = -80.201226 Pseudo R2 = 0.7748
------------------------------------------------------------------------------
acc | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
t6569 | .7536172 .1487663 5.07 0.000 .4620406 1.045194
t7074 | 1.050336 .1575621 6.67 0.000 .7415201 1.359152
t7579 | .6998992 .2203023 3.18 0.001 .2681146 1.131684
o7579 | .3872451 .1181021 3.28 0.001 .1557692 .618721
logm | 1 . . . . .
_cons | -6.946953 .1269425 -54.73 0.000 -7.195756 -6.69815
------------------------------------------------------------------------------
lrtest, using(0)
Poisson: likelihood-ratio test chi2(4) = 23.57
Prob > chi2 = 0.0001
* Stata 8 code.
poisgof
* Stata 9 code and output.
estat gof
Goodness-of-fit chi2 = 62.53587
Prob > chi2(28) = 0.0002
poisson acc tb tc td te o7579 logm, const(1)
Iteration 0: log likelihood = -1135.6024
Iteration 1: log likelihood = -92.22882
Iteration 2: log likelihood = -84.118981
Iteration 3: log likelihood = -84.115144
Iteration 4: log likelihood = -84.115144
Poisson regression Number of obs = 34
LR chi2(6) = 544.18
Prob > chi2 = 0.0000
Log likelihood = -84.115144 Pseudo R2 = 0.7639
------------------------------------------------------------------------------
acc | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
tb | -.7437271 .1691475 -4.40 0.000 -1.07525 -.412204
tc | -.7548676 .3276393 -2.30 0.021 -1.397029 -.1127063
td | -.1843232 .2875527 -0.64 0.522 -.7479161 .3792697
te | .3841932 .23479 1.64 0.102 -.0759868 .8443732
o7579 | .5000988 .1115645 4.48 0.000 .2814363 .7187612
logm | 1 . . . . .
_cons | -5.799973 .1784196 -32.51 0.000 -6.149669 -5.450278
------------------------------------------------------------------------------
lrtest, using(0)
Poisson: likelihood-ratio test chi2(3) = 31.40
Prob > chi2 = 0.0000
* Stata 8 code.
poisgof
* Stata 9 code and output.
estat gof
Goodness-of-fit chi2 = 70.36371
Prob > chi2(27) = 0.0000