Table 2.1, page 17.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/afterlife, clear
list
+--------------------------+
| gender aftlife freq |
|--------------------------|
1. | females yes 435 |
2. | females no 147 |
3. | male yes 375 |
4. | male no 134 |
+--------------------------+
Notice that both variables gender and aftlife are numeric variables. They have value labels. We can also do:
list, nolab
+-------------------------+
| gender aftlife freq |
|-------------------------|
1. | 1 1 435 |
2. | 1 0 147 |
3. | 0 1 375 |
4. | 0 0 134 |
+-------------------------+
Table 2.2, page 18.
tab gender aftlife [fweight=freq]
| belief in afterlife
gender | no yes | Total
-----------+----------------------+----------
male | 134 375 | 509
females | 147 435 | 582
-----------+----------------------+----------
Total | 281 810 | 1,091
Calculation in Section 2.1.2, page 18.
tab gender aftlife [fweight=freq], cell row
+-----------------+
| Key |
|-----------------|
| frequency |
| row percentage |
| cell percentage |
+-----------------+
| belief in afterlife
gender | no yes | Total
-----------+----------------------+----------
male | 134 375 | 509
| 26.33 73.67 | 100.00
| 12.28 34.37 | 46.65
-----------+----------------------+----------
females | 147 435 | 582
| 25.26 74.74 | 100.00
| 13.47 39.87 | 53.35
-----------+----------------------+----------
Total | 281 810 | 1,091
| 25.76 74.24 | 100.00
| 25.76 74.24 | 100.00
Calculation on difference of proportions in Section 2.2.1, page 20. The Stata command cs is part of epitab for creating tables for epidemiologists and you can do help epitab for more information on it. It is used mostly for case-control studies.
cs aftlife gender [fweight=freq]
| gender |
| Exposed Unexposed | Total
-----------------+------------------------+----------
Cases | 435 375 | 810
Noncases | 147 134 | 281
-----------------+------------------------+----------
Total | 582 509 | 1091
| |
Risk | .7474227 .7367387 | .7424381
| |
| Point estimate | [95% Conf. Interval]
|------------------------+----------------------
Risk difference | .010684 | -.0413721 .0627401
Risk ratio | 1.014502 | .9457309 1.088273
Attr. frac. ex. | .0142944 | -.0573833 .0811133
Attr. frac. pop | .0076766 |
+-----------------------------------------------
chi2(1) = 0.16 Pr>chi2 = 0.6872
Section 2.2.2, Table 2.3 and calculation on page 20 and 21 including relative risk.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/aspirin, clear
tab group mi [fweight=count]
| mi
group | no yes | Total
-----------+----------------------+----------
aspirin | 10,933 104 | 11,037
placebo | 10,845 189 | 11,034
-----------+----------------------+----------
Total | 21,778 293 | 22,071
cs mi group [fweight=count]
| group |
| Exposed Unexposed | Total
-----------------+------------------------+----------
Cases | 189 104 | 293
Noncases | 10845 10933 | 21778
-----------------+------------------------+----------
Total | 11034 11037 | 22071
| |
Risk | .0171289 .0094229 | .0132753
| |
| Point estimate | [95% Conf. Interval]
|------------------------+----------------------
Risk difference | .007706 | .0046878 .0107243
Risk ratio | 1.817802 | 1.433031 2.305884
Attr. frac. ex. | .449885 | .3021783 .5663269
Attr. frac. pop | .2901989 |
+-----------------------------------------------
chi2(1) = 25.01 Pr>chi2 = 0.0000
Section 2.3.2 and Section 2.3.3, page 23-25. Odds Ratio for Aspirin Study.
logit mi group [fweight=count], or
Logistic regression Number of obs = 22071
LR chi2(1) = 25.37
Prob > chi2 = 0.0000
Log likelihood = -1544.6617 Pseudo R2 = 0.0081
------------------------------------------------------------------------------
mi | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
group | 1.832054 .2250524 4.93 0.000 1.440042 2.33078
------------------------------------------------------------------------------
logit mi group [fweight=count]
Iteration 0: log likelihood = -1557.3477
Iteration 1: log likelihood = -1544.9244
Iteration 2: log likelihood = -1544.6619
Iteration 3: log likelihood = -1544.6617
Logit estimates Number of obs = 22071
LR chi2(1) = 25.37
Prob > chi2 = 0.0000
Log likelihood = -1544.6617 Pseudo R2 = 0.0081
------------------------------------------------------------------------------
mi | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
group | .6054377 .1228416 4.93 0.000 .3646726 .8462028
_cons | -4.65515 .0985233 -47.25 0.000 -4.848252 -4.462048
------------------------------------------------------------------------------
Table 2.4 and calculations on page 26.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/table2_4, clear
tab smoke mi [fw=count], col
+-------------------+
| Key |
|-------------------|
| frequency |
| column percentage |
+-------------------+
| mi
smoke | control MI | Total
-----------+----------------------+----------
no | 346 90 | 436
| 66.67 34.35 | 55.83
-----------+----------------------+----------
yes | 173 172 | 345
| 33.33 65.65 | 44.17
-----------+----------------------+----------
Total | 519 262 | 781
| 100.00 100.00 | 100.00
logit mi smoke [fw=count], or
Iteration 0: log likelihood = -498.26482
Iteration 1: log likelihood = -461.5178
Iteration 2: log likelihood = -461.1358
Iteration 3: log likelihood = -461.13566
Logit estimates Number of obs = 781
LR chi2(1) = 74.26
Prob > chi2 = 0.0000
Log likelihood = -461.13566 Pseudo R2 = 0.0745
------------------------------------------------------------------------------
mi | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
smoke | 3.822222 .6115027 8.38 0.000 2.793415 5.229936
------------------------------------------------------------------------------
Table 2.5 and calculations on page 31.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/party, clear
tab male party [fw=count], expected
+--------------------+
| Key |
|--------------------|
| frequency |
| expected frequency |
+--------------------+
| party
male | 1 2 3 | Total
-----------+---------------------------------+----------
0 | 279 73 225 | 577
| 261.4 70.7 244.9 | 577.0
-----------+---------------------------------+----------
1 | 165 47 191 | 403
| 182.6 49.3 171.1 | 403.0
-----------+---------------------------------+----------
Total | 444 120 416 | 980
| 444.0 120.0 416.0 | 980.0
tab male party [fw=count], chi2 lrchi2
| party
male | 1 2 3 | Total
-----------+---------------------------------+----------
0 | 279 73 225 | 577
1 | 165 47 191 | 403
-----------+---------------------------------+----------
Total | 444 120 416 | 980
Pearson chi2(2) = 7.0095 Pr = 0.030
likelihood-ratio chi2(2) = 7.0026 Pr = 0.030
Table 2.6 and calculation on page 32. Stata’s tabulate command does not produce adjusted residuals. Nicholas J. Cox has written a module for tabulation and chi-square tasks. You can download it from the internet by typing search tabchi (see How can I use the search command to search for programs and get additional help? for more information about using search).
tabchi male party [fw=count], a
observed frequency
expected frequency
adjusted residual
-------------------------------------
| party
male | 1 2 3
----------+--------------------------
0 | 279 73 225
| 261.416 70.653 244.931
| 2.293 0.465 -2.618
|
1 | 165 47 191
| 182.584 49.347 171.069
| -2.293 -0.465 2.618
-------------------------------------
Pearson chi2(2) = 7.0095 Pr = 0.030
likelihood-ratio chi2(2) = 7.0026 Pr = 0.030
gen p1=party-1
cc p1 male [fw=count] if party ~=2
Proportion
| Exposed Unexposed | Total Exposed
-----------------+------------------------+----------------------
Cases | 191 225 | 416 0.4591
Controls | 165 279 | 444 0.3716
-----------------+------------------------+----------------------
Total | 356 504 | 860 0.4140
| |
| Point estimate | [95% Conf. Interval]
|------------------------+----------------------
Odds ratio | 1.435394 | 1.082895 1.902763 (exact)
Attr. frac. ex. | .3033271 | .0765493 .4744484 (exact)
Attr. frac. pop | .139268 |
+-----------------------------------------------
chi2(1) = 6.78 Pr>chi2 = 0.0092
Section 2.4.6, page 33. Partitioning Chi-squared.
tab male party [fw=count] if party~=3, lrchi2
| party
male | 1 2 | Total
-----------+----------------------+----------
0 | 279 73 | 352
1 | 165 47 | 212
-----------+----------------------+----------
Total | 444 120 | 564
likelihood-ratio chi2(1) = 0.1612 Pr = 0.688
gen np = 0
replace np = 1 if party ==3
preserve
collapse (sum) count, by(male np)
list
+-------------------+
| male np count |
|-------------------|
1. | 0 0 352 |
2. | 0 1 225 |
3. | 1 0 212 |
4. | 1 1 191 |
+-------------------+
tab male np [fw=count] ,lrchi2
| np
male | 0 1 | Total
-----------+----------------------+----------
0 | 352 225 | 577
1 | 212 191 | 403
-----------+----------------------+----------
Total | 564 416 | 980
likelihood-ratio chi2(1) = 6.8414 Pr = 0.009
restore
tab male party [fw=count] ,lrchi2
| party
male | 1 2 3 | Total
-----------+---------------------------------+----------
0 | 279 73 225 | 577
1 | 165 47 191 | 403
-----------+---------------------------------+----------
Total | 444 120 416 | 980
likelihood-ratio chi2(2) = 7.0026 Pr = 0.030
Section 2.5.2, Table 2.7 on page 35 and calculation on page 36.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/alcohol, clear
tab alcohol mal [fw=count], r
+----------------+
| Key |
|----------------|
| frequency |
| row percentage |
+----------------+
| mal
alcohol | no yes | Total
-----------+----------------------+----------
0 | 17,066 48 | 17,114
| 99.72 0.28 | 100.00
-----------+----------------------+----------
<1 | 14,464 38 | 14,502
| 99.74 0.26 | 100.00
-----------+----------------------+----------
1-2 | 788 5 | 793
| 99.37 0.63 | 100.00
-----------+----------------------+----------
3-5 | 126 1 | 127
| 99.21 0.79 | 100.00
-----------+----------------------+----------
>=6 | 37 1 | 38
| 97.37 2.63 | 100.00
-----------+----------------------+----------
Total | 32,481 93 | 32,574
| 99.71 0.29 | 100.00
tabchi alcohol mal [fw=count], a
observed frequency
expected frequency
adjusted residual
--------------------------------
| mal
alcohol | no yes
----------+---------------------
0 | 17066 48
| 17065.139 48.861
| 0.179 -0.179
|
<1 | 14464 38
| 14460.596 41.404
| 0.711 -0.711
|
1-2 | 788 5
| 790.736 2.264
| -1.843 1.843
|
3-5 | 126 1
| 126.637 0.363
| -1.062 1.062
|
>=6 | 37 1
| 37.892 0.108
| -2.712 2.712
--------------------------------
3 cells with expected frequency < 5
2 cells with expected frequency < 1
Pearson chi2(4) = 12.0821 Pr = 0.017
likelihood-ratio chi2(4) = 6.2020 Pr = 0.185
For the M-squared statistics, we can manually compute it as follows.
recode alcohol 0 = 0 1 = .5 2 = 1.5 3 = 4 4 = 7, gen(ascore)
corr ascore mal [fw=count]
(obs=32574)
| ascore mal
-------------+------------------
ascore | 1.0000
mal | 0.0142 1.0000
di r(N)*r(rho)^2
6.5701339
Calculation on page 37 in Section 2.5.4.
corr alcohol mal [fw=count]
(obs=32574)
| alcohol mal
-------------+------------------
alcohol | 1.0000
mal | 0.0075 1.0000
di r(N)*r(rho)^2
1.8278158
expand count
(32564 observations created)
egen mrank = rank(alcohol)
corr mrank mal
(obs=32574)
| mrank mal
-------------+------------------
mrank | 1.0000
mal | 0.0033 1.0000
di r(N)*r(rho)^2
.35143832
Section 2.6.2, page 41. Fisher’s Tea Taster.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/fisher_tea, clear
tab pour guess [fw=count] , exact all
| guess
pour | milk tea | Total
-----------+----------------------+----------
milk | 3 1 | 4
tea | 1 3 | 4
-----------+----------------------+----------
Total | 4 4 | 8
Pearson chi2(1) = 2.0000 Pr = 0.157
likelihood-ratio chi2(1) = 2.0930 Pr = 0.148
Cramer's V = 0.5000
gamma = 0.8000 ASE = 0.294
Kendall's tau-b = 0.5000 ASE = 0.306
Fisher's exact = 0.486
1-sided Fisher's exact = 0.243
Table 2.9 on page 41. You need to download a module called _GHYPER by Nick Cox and then you can use the egen command to generate the hypergeometric probabilities (see How can I use the search command to search for programs and get additional help? for more information about using search).
clear
set obs 5
obs was 0, now 5
gen n = _n -1
egen prob = hyper(n 4 4 8)
list
+---------------+
| n prob |
|---------------|
1. | 0 .01428571 |
2. | 1 .22857143 |
3. | 2 .51428571 |
4. | 3 .22857143 |
5. | 4 .01428571 |
+---------------+
gen a = sum(prob)
gen pvalue = 1
replace pvalue = 1 - a[_n-1] if _n>=2
list
+-------------------------------------+
| n prob a pvalue |
|-------------------------------------|
1. | 0 .01428571 .0142857 1 |
2. | 1 .22857143 .2428571 .9857143 |
3. | 2 .51428571 .7571428 .7571428 |
4. | 3 .22857143 .9857143 .2428572 |
5. | 4 .01428571 1 .0142857 |
+-------------------------------------+
drop a
gen chi2 = ( (n-2)^2 + (4-n -2)^2 + (4-n-2)^2 + (n-2)^2 ) /2
list
+---------------------------------+
| n prob pvalue chi2 |
|---------------------------------|
1. | 0 .01428571 1 8 |
2. | 1 .22857143 .9857143 2 |
3. | 2 .51428571 .7571428 0 |
4. | 3 .22857143 .2428572 2 |
5. | 4 .01428571 .0142857 8 |
+---------------------------------+
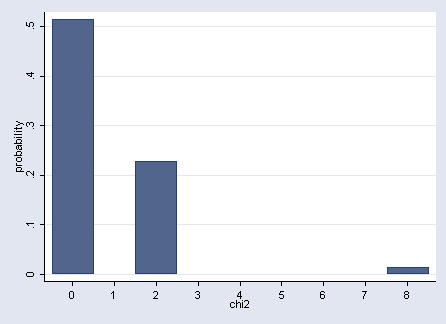
Figure 2.2 on page 42.
gen y2=0 graph twoway rbar prob y2 chi2, xlabel(0 1 to 8) ytitle(probability)
Section 2.6.4, page 44 using tea-tasting data. The command exactcc can be downloaded from the internet by typing search exactcc in the command line (see How can I use the search command to search for programs and get additional help? for more information about using search).
exactcc pour guess [fw=count] , exact
| guess | Proportion
| Exposed Unexposed | Total Exposed
-----------------+------------------------+----------------------
Cases | 3 1 | 4 0.7500
Controls | 1 3 | 4 0.2500
-----------------+------------------------+----------------------
Total | 4 4 | 8 0.5000
| |
| Point estimate | [95% Conf. Interval]
|------------------------+----------------------
| | Cornfield's limits
Odds ratio | 9 | .1938699 . Adjusted
| | .4800561 . Unadjusted
| | Exact limits
| | .2117353 626.24
| | Cornfield's limits
Attr. frac. ex. | .8888889 | -4.158098 . Adjusted
| | -1.08309 . Unadjusted
| | Exact limits
| | -3.722879 .9984032
Attr. frac. pop | .6666667 |
+-----------------------------------------------
chi2(1) = 2.00 Pr>chi2 = 0.1573
Yates' adjusted chi2(1) = 0.50 Pr>chi2 = 0.4795
1-sided Fisher's exact P = 0.2429
2-sided Fisher's exact P = 0.4857
2 times 1-sided Fisher's exact P = 0.4857