Table 4.1, page 75.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/snoring, clear
tab snoring heart [fw=count], row
+----------------+
| Key |
|----------------|
| frequency |
| row percentage |
+----------------+
| heart
snoring | 0 1 | Total
-----------+----------------------+----------
0 | 1,355 24 | 1,379
| 98.26 1.74 | 100.00
-----------+----------------------+----------
2 | 603 35 | 638
| 94.51 5.49 | 100.00
-----------+----------------------+----------
4 | 192 21 | 213
| 90.14 9.86 | 100.00
-----------+----------------------+----------
5 | 224 30 | 254
| 88.19 11.81 | 100.00
-----------+----------------------+----------
Total | 2,374 110 | 2,484
| 95.57 4.43 | 100.00
reg heart snoring [fw=count]
Source | SS df MS Number of obs = 2484
-------------+------------------------------ F( 1, 2482) = 74.82
Model | 3.07633377 1 3.07633377 Prob > F = 0.0000
Residual | 102.052491 2482 .041117039 R-squared = 0.0293
-------------+------------------------------ Adj R-squared = 0.0289
Total | 105.128824 2483 .042339438 Root MSE = .20277
------------------------------------------------------------------------------
heart | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
snoring | .020038 .0023166 8.65 0.000 .0154954 .0245806
_cons | .0168723 .0051571 3.27 0.001 .0067598 .0269849
------------------------------------------------------------------------------
predict ylin
(option xb assumed; fitted values)
logit heart snoring [fw=count]
Logit estimates Number of obs = 2484
LR chi2(1) = 63.10
Prob > chi2 = 0.0000
Log likelihood = -418.86582 Pseudo R2 = 0.0700
------------------------------------------------------------------------------
heart | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
snoring | .3973366 .0500106 7.95 0.000 .2993176 .4953557
_cons | -3.866248 .1662144 -23.26 0.000 -4.192022 -3.540474
------------------------------------------------------------------------------
predict ylogit
(option p assumed; Pr(heart))
probit heart snoring [fw=count]
Probit estimates Number of obs = 2484
LR chi2(1) = 64.03
Prob > chi2 = 0.0000
Log likelihood = -418.39714 Pseudo R2 = 0.0711
------------------------------------------------------------------------------
heart | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
snoring | .1877705 .02363 7.95 0.000 .1414565 .2340844
_cons | -2.060552 .0704491 -29.25 0.000 -2.198629 -1.922474
------------------------------------------------------------------------------
predict yprob
(option p assumed; Pr(heart))
list if heart==1
+----------------------------------------------------------+
| snoring heart count ylin ylogit yprob |
|----------------------------------------------------------|
1. | 0 1 24 .0168723 .0205074 .0196729 |
2. | 2 1 35 .0569483 .0442951 .0459933 |
3. | 4 1 21 .0970243 .0930541 .0951876 |
4. | 5 1 30 .1170623 .1324389 .1309952 |
+----------------------------------------------------------+
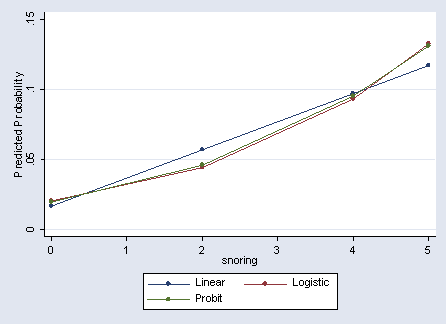
Figure 4.1 on page 76.
label variable ylin "Linear" label variable ylogit "Logistic" label variable yprob "Probit" graph twoway connect ylin ylogit yprob snoring, ytitle(Predicted Probability)
Section 4.3.2, page 84. An example using horseshoe crabs data.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
glm satell width , family(poisson) nolog
Generalized linear models No. of obs = 173
Optimization : ML: Newton-Raphson Residual df = 171
Scale parameter = 1
Deviance = 567.878575 (1/df) Deviance = 3.320927
Pearson = 544.1570201 (1/df) Pearson = 3.182205
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -461.5881235 AIC = 5.3594
BIC = -313.3342876
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .1640451 .0199653 8.22 0.000 .1249137 .2031764
_cons | -3.304757 .5422416 -6.09 0.000 -4.367531 -2.241983
------------------------------------------------------------------------------
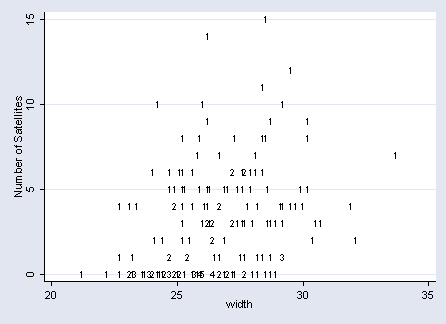
Figure 4.3 on page 84.
sort satell width by satell width: gen count=_N graph twoway scatter satell width, mlabel(count) mlabcolor(black) ytitle(Number of Satellites) msize(tiny)
glm satell width if width <=33 , family(poisson) nolog
Generalized linear models No. of obs = 172
Optimization : ML: Newton-Raphson Residual df = 170
Scale parameter = 1
Deviance = 567.3393552 (1/df) Deviance = 3.33729
Pearson = 544.0694946 (1/df) Pearson = 3.200409
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -459.4147233 AIC = 5.365287
BIC = -307.7347058
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .1699846 .0216086 7.87 0.000 .1276325 .2123368
_cons | -3.461006 .584658 -5.92 0.000 -4.606915 -2.315098
------------------------------------------------------------------------------
glm satell width , family(poisson) link(identity) nolog
Generalized linear models No. of obs = 173
Optimization : ML: Newton-Raphson Residual df = 171
Scale parameter = 1
Deviance = 557.7083301 (1/df) Deviance = 3.261452
Pearson = 542.4855164 (1/df) Pearson = 3.17243
Variance function: V(u) = u [Poisson]
Link function : g(u) = u [Identity]
Standard errors : OIM
Log likelihood = -456.503001 AIC = 5.300613
BIC = -323.5045326
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .5494969 .0592926 9.27 0.000 .4332856 .6657082
_cons | -11.53206 1.510399 -7.64 0.000 -14.49239 -8.57173
------------------------------------------------------------------------------
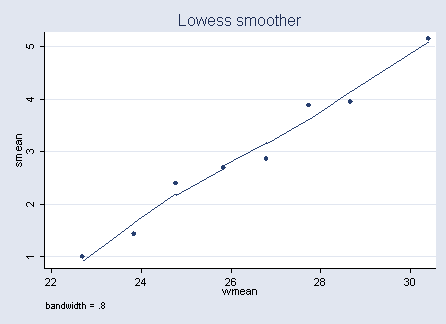
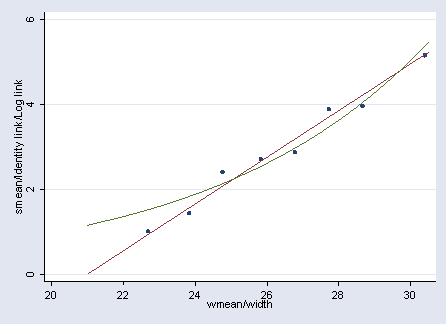
Figure 4.4 on page 85.
gen a = ceil(width - 23.25) + 1 replace a = 1 if a<=0 replace a = 8 if a >8 sort a by a: egen smean = mean(satell) by a: egen wmean=mean(width) lowess smean wmean
glm satell width, family(poisson) nolog predict ylog label variable ylog "Log link" glm satell width , family(poisson) link(identity) nolog predict ylin label variable ylin "Identity link" graph twoway scatter smean wmean || line ylin ylog width if ylog<=6, legend(off)
Section 4.3.4, page 87. Horseshoe crab data.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
sort width
collapse (sum) satell (count) n, by(width)
glm satell width, fam(poi) lnoff(n) nolog
Generalized linear models No. of obs = 66
Optimization : ML: Newton-Raphson Residual df = 64
Scale parameter = 1
Deviance = 190.0272196 (1/df) Deviance = 2.969175
Pearson = 174.2737318 (1/df) Pearson = 2.723027
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -199.2592131 AIC = 6.098764
BIC = -78.11068387
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .1640451 .0199653 8.22 0.000 .1249137 .2031764
_cons | -3.304757 .5422416 -6.09 0.000 -4.367531 -2.241983
n | (exposure)
------------------------------------------------------------------------------
Section 4.4.2 on Poisson model checking, a simpler approach on page 90.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
replace a = 8 if a >8
sort a
collapse (mean) width (sum) satell n, by(a)
glm satell width, fam(poi) lnoff(n)
Generalized linear models No. of obs = 8
Optimization : ML: Newton-Raphson Residual df = 6
Scale parameter = 1
Deviance = 6.516421366 (1/df) Deviance = 1.08607
Pearson = 6.246497819 (1/df) Pearson = 1.041083
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -26.48068535 AIC = 7.120171
BIC = -5.960227884
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .1728976 .0212529 8.14 0.000 .1312427 .2145525
_cons | -3.540176 .5765828 -6.14 0.000 -4.670258 -2.410095
n | (exposure)
------------------------------------------------------------------------------
Section 4.4.3, page 90. Model Residuals.
glm satell width, fam(poi) lnoff(n)
Generalized linear models No. of obs = 8
Optimization : ML: Newton-Raphson Residual df = 6
Scale parameter = 1
Deviance = 6.516421366 (1/df) Deviance = 1.08607
Pearson = 6.246497819 (1/df) Pearson = 1.041083
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -26.48068535 AIC = 7.120171
BIC = -5.960227884
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .1728976 .0212529 8.14 0.000 .1312427 .2145525
_cons | -3.540176 .5765828 -6.14 0.000 -4.670258 -2.410095
n | (exposure)
------------------------------------------------------------------------------
predict count
(option mu assumed; predicted mean satell)
predict resid, p
predict h, h
gen aresid = resid/sqrt(1-h)
drop h
list
+---------------------------------------------------------------+
| a width satell n count resid aresid |
|---------------------------------------------------------------|
1. | 1 22.69286 14 14 20.54098 -1.443218 -1.630687 |
2. | 2 23.84286 20 14 25.05952 -1.010702 -1.106694 |
3. | 3 24.775 67 28 58.88382 1.057679 1.224653 |
4. | 4 25.83846 105 39 98.5726 .6473766 .7527656 |
5. | 5 26.79091 63 22 65.55898 -.3160459 -.3391854 |
|---------------------------------------------------------------|
6. | 6 27.7375 93 24 84.2362 .9548676 1.057612 |
7. | 7 28.66667 71 18 74.18733 -.3700516 -.4229863 |
8. | 8 30.40714 72 14 77.96057 -.6750725 -1.00809 |
+---------------------------------------------------------------+
Section 4.4.4, page 92-93. Overdispersion in Poisson regression
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
replace a = 8 if a >8
sort a
egen sd = sd(satell), by(a)
gen var=sd*sd
collapse (mean) width satell var (sum) tsat =satell (count) n, by(a)
list
+-----------------------------------------------+
| a width satell var tsat n |
|-----------------------------------------------|
1. | 1 22.69286 1 2.769231 14 14 |
2. | 2 23.84286 1.42857 8.879121 20 14 |
3. | 3 24.775 2.39286 6.543651 67 28 |
4. | 4 25.83846 2.69231 11.37652 105 39 |
5. | 5 26.79091 2.86364 6.885281 63 22 |
|-----------------------------------------------|
6. | 6 27.7375 3.875 8.809782 93 24 |
7. | 7 28.66667 3.94444 16.87909 71 18 |
8. | 8 30.40714 5.14286 8.285714 72 14 |
+-----------------------------------------------+
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
sort width
collapse (sum) satell (count) n, by(width)
glm satell width, fam(poi) lnoff(n)
Generalized linear models No. of obs = 66
Optimization : ML: Newton-Raphson Residual df = 64
Scale parameter = 1
Deviance = 190.0272196 (1/df) Deviance = 2.969175
Pearson = 174.2737318 (1/df) Pearson = 2.723027
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -199.2592131 AIC = 6.098764
BIC = -78.11068387
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .1640451 .0199653 8.22 0.000 .1249137 .2031764
_cons | -3.304757 .5422416 -6.09 0.000 -4.367531 -2.241983
n | (exposure)
------------------------------------------------------------------------------
di sqrt(2.723027)
1.6501597
glm satell width, fam(poi) lnoff(n) scale(x2)
Generalized linear models No. of obs = 66
Optimization : ML: Newton-Raphson Residual df = 64
Scale parameter = 1
Deviance = 190.0272196 (1/df) Deviance = 2.969175
Pearson = 174.2737318 (1/df) Pearson = 2.723027
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -199.2592131 AIC = 6.098764
BIC = -78.11068387
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .1640451 .032946 4.98 0.000 .0994721 .2286181
_cons | -3.304757 .8947852 -3.69 0.000 -5.058504 -1.55101
n | (exposure)
------------------------------------------------------------------------------
(Standard errors scaled using square root of Pearson X2-based dispersion)
di 4.98^2
24.8004