This chapter makes extensive use of the fitstat program, which is not part of base Stata. Prior to using the fitstat command, they need to be downloaded by typing search fitstat in the command line (see How can I use the search command to search for programs and get additional help? for more information about using search).
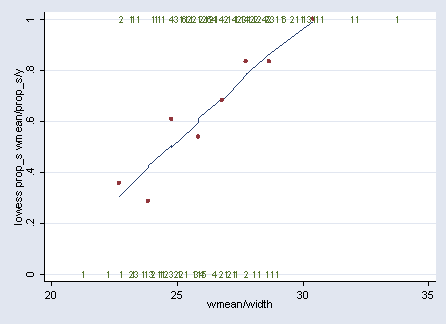
Figure 5.2, page 105. Using crab data set.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear gen a = ceil(width - 23.25) + 1 replace a = 1 if a<=0 replace a = 8 if a >8 sort a egen wmean = mean(width), by(a) * Stata 8 code. egen ssatell = sum(y), by(a) egen sn = sum(n), by(a) * Stata 9 code. egen ssatell = total(y), by(a) egen sn = total(n), by(a) gen prop_s = ssatell/sn graph twoway (lowess prop_s wmean) (scatter prop_s wmean) /// (scatter y width , mlab(marker) msymbol(none) legend(off))
logit y width, nolog
Logit estimates Number of obs = 173
LR chi2(1) = 31.31
Prob > chi2 = 0.0000
Log likelihood = -97.226331 Pseudo R2 = 0.1387
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .4972306 .1017361 4.89 0.000 .2978316 .6966297
_cons | -12.35082 2.628731 -4.70 0.000 -17.50304 -7.1986
------------------------------------------------------------------------------
Table 5.1 on page 106.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
replace a = 8 if a >8
sort a
quietly logit y width, nolog
predict p
collapse (mean) width p (sum) y p_count=p n , by(a)
gen prop = y/n
list
+---------------------------------------------------------+
| a width p y p_count n prop |
|---------------------------------------------------------|
1. | 1 22.69286 .2596734 5 3.635427 14 .3571429 |
2. | 2 23.84286 .3789991 4 5.305987 14 .2857143 |
3. | 3 24.775 .492058 17 13.77762 28 .6071429 |
4. | 4 25.83846 .6212226 21 24.22768 39 .5384616 |
5. | 5 26.79091 .7244455 15 15.9378 22 .6818182 |
|---------------------------------------------------------|
6. | 6 27.7375 .8076395 20 19.38335 24 .8333333 |
7. | 7 28.66667 .8694543 15 15.65018 18 .8333333 |
8. | 8 30.40714 .9344253 14 13.08195 14 1 |
+---------------------------------------------------------+
Linear model approach on page 106.
reg y width
Source | SS df MS Number of obs = 173
-------------+------------------------------ F( 1, 171) = 32.85
Model | 6.40974521 1 6.40974521 Prob > F = 0.0000
Residual | 33.3706016 171 .195149717 R-squared = 0.1611
-------------+------------------------------ Adj R-squared = 0.1562
Total | 39.7803468 172 .231281086 Root MSE = .44176
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .0915308 .0159709 5.73 0.000 .0600052 .1230563
_cons | -1.765534 .4213581 -4.19 0.000 -2.597267 -.9338014
------------------------------------------------------------------------------
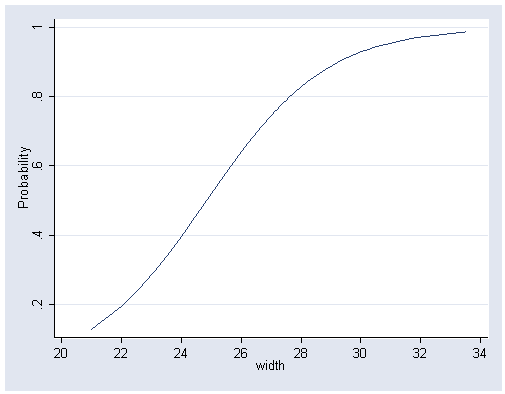
Back to logit model on page 107 and Figure 5.1, page 104.
quietly logit y width
predict p
tablist width p, sort(v)
+-------------------------+
| width p Freq |
|-------------------------|
| 21 .129096 1 |
| 22 .195959 1 |
| 22.5 .2380991 3 |
| 22.9 .2760306 3 |
| 23 .286077 2 |
|-------------------------|
| 23.1 .2963393 3 |
| 23.2 .3068116 1 |
| 23.4 .3283577 1 |
| 23.5 .3394157 1 |
| 23.7 .3620558 3 |
|-------------------------|
| 23.8 .3736171 3 |
| 23.9 .3853249 1 |
| 24 .3971669 2 |
| 24.1 .4091306 1 |
| 24.2 .4212029 2 |
|-------------------------|
| 24.3 .4333699 2 |
| 24.5 .4579326 7 |
| 24.7 .4827014 5 |
| 24.8 .4951253 1 |
| 24.9 .5075554 3 |
|-------------------------|
| 25 .5199761 6 |
| 25.1 .5323722 2 |
| 25.2 .5447285 2 |
| 25.3 .5570297 1 |
| 25.4 .5692616 3 |
|-------------------------|
| 25.5 .5814095 3 |
| 25.6 .5934595 2 |
| 25.7 .6053981 6 |
| 25.8 .6172119 7 |
| 25.9 .6288891 1 |
|-------------------------|
| 26 .6404177 6 |
| 26.1 .6517864 2 |
| 26.2 .6629848 8 |
| 26.3 .674003 1 |
| 26.5 .6954646 6 |
|-------------------------|
| 26.7 .7161084 3 |
| 26.8 .7261074 3 |
| 27 .7454343 5 |
| 27.1 .7547542 2 |
| 27.2 .763841 2 |
|-------------------------|
| 27.3 .7726924 1 |
| 27.4 .7813072 3 |
| 27.5 .7896843 6 |
| 27.6 .7978235 1 |
| 27.7 .8057253 2 |
|-------------------------|
| 27.8 .8133904 2 |
| 27.9 .8208204 2 |
| 28 .8280171 3 |
| 28.2 .8417205 4 |
| 28.3 .8482328 3 |
|-------------------------|
| 28.4 .8545237 2 |
| 28.5 .8605966 4 |
| 28.7 .8721051 2 |
| 28.9 .8827927 1 |
| 29 .8878404 6 |
|-------------------------|
| 29.3 .9018577 2 |
| 29.5 .9103148 1 |
| 29.7 .9181093 1 |
| 29.8 .9217708 1 |
| 30 .9286477 3 |
|-------------------------|
| 30.2 .9349627 1 |
| 30.3 .9379216 1 |
| 30.5 .9434658 1 |
| 31.7 .9680587 1 |
| 31.9 .9709946 1 |
|-------------------------|
| 33.5 .9866974 1 |
+-------------------------+
sum p
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
p | 173 .6416185 .1980444 .129096 .9866974
graph twoway line p width, ytitle("Probability") xlabel(20(2)34) sort
Section 5.1.3, page 107-108. Odds ratio interpretation.
Note: You may have to download the program prvalue from the internet. It belongs a suite of programs written by J. Scott Long and Jeremy Freese for post estimation (see How can I use the search command to search for programs and get additional help? for more information about using search).
logit y width, or nolog
Logit estimates Number of obs = 173
LR chi2(1) = 31.31
Prob > chi2 = 0.0000
Log likelihood = -97.226331 Pseudo R2 = 0.1387
------------------------------------------------------------------------------
y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | 1.644162 .1672706 4.89 0.000 1.346935 2.006977
------------------------------------------------------------------------------
prvalue, x(width=26.3)
logit: Predictions for y
Pr(y=1|x): 0.6740 95% ci: (0.5915,0.7470)
Pr(y=0|x): 0.3260 95% ci: (0.2530,0.4085)
width
x= 26.3
di .6740/.3260
2.0674847
prvalue, x(width=27.3)
logit: Predictions for y
Pr(y=1|x): 0.7727 95% ci: (0.6830,0.8428)
Pr(y=0|x): 0.2273 95% ci: (0.1572,0.3170)
width
x= 27.3
di .7727/.2273
3.3994721
di 3.3994721/2.0674847
1.644255
Section 5.2.1, page 109. Confidence intervals for effects.
logit y width, nolog
Logit estimates Number of obs = 173
LR chi2(1) = 31.31
Prob > chi2 = 0.0000
Log likelihood = -97.226331 Pseudo R2 = 0.1387
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .4972306 .1017361 4.89 0.000 .2978316 .6966297
_cons | -12.35082 2.628731 -4.70 0.000 -17.50304 -7.1986
------------------------------------------------------------------------------
logit y width, or nolog
Logit estimates Number of obs = 173
LR chi2(1) = 31.31
Prob > chi2 = 0.0000
Log likelihood = -97.226331 Pseudo R2 = 0.1387
------------------------------------------------------------------------------
y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | 1.644162 .1672706 4.89 0.000 1.346935 2.006977
------------------------------------------------------------------------------
Section 5.3. Model checking.
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
(2 real changes made)
replace a = 8 if a >8
(5 real changes made)
sort a
logit satell width, nolog
Logit estimates Number of obs = 173
LR chi2(1) = 31.31
Prob > chi2 = 0.0000
Log likelihood = -97.226331 Pseudo R2 = 0.1387
------------------------------------------------------------------------------
satell | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .4972306 .1017361 4.89 0.000 .2978316 .6966297
_cons | -12.35082 2.628731 -4.70 0.000 -17.50304 -7.1986
------------------------------------------------------------------------------
predict p
(option p assumed; Pr(satell))
gen no=1-y
gen nop = 1-p
collapse (sum) yes=y no p nop, by(a)
list
+------------------------------------+
| a yes no p nop |
|------------------------------------|
1. | 1 5 9 3.635427 10.36457 |
2. | 2 4 10 5.305987 8.694013 |
3. | 3 17 11 13.77762 14.22238 |
4. | 4 21 18 24.22768 14.77232 |
5. | 5 15 7 15.9378 6.0622 |
|------------------------------------|
6. | 6 20 4 19.38335 4.616651 |
7. | 7 15 3 15.65018 2.349822 |
8. | 8 14 0 13.08195 .9180457 |
+------------------------------------+
gen x2 = (yes-p)^2/p + (no-nop)^2/nop
* Stata 8 code.
egen x2sum = sum(x2)
* Stata 9 code.
egen x2sum = total(x2)
gen g2 = 2*yes*log(yes/p) + 2*no*log(no/nop)
(1 missing value generated)
replace g2 = 2 if yes==0 | no==0
(1 real change made)
* Stata 8 code.
egen g2sum=sum(g2)
* Stata 9 code.
egen g2sum=total(g2)
list
+------------------------------------------------------------------------------+
| a yes no p nop x2 x2sum g2 g2sum |
|------------------------------------------------------------------------------|
1. | 1 5 9 3.635427 10.36457 .6918539 5.3201 .6460713 6.280302 |
2. | 2 4 10 5.305987 8.694013 .5176301 5.3201 .5386781 6.280302 |
3. | 3 17 11 13.77762 14.22238 1.483761 5.3201 1.493428 6.280302 |
4. | 4 21 18 24.22768 14.77232 1.135233 5.3201 1.109317 6.280302 |
5. | 5 15 7 15.9378 6.0622 .2002557 5.3201 .1944201 6.280302 |
|------------------------------------------------------------------------------|
6. | 6 20 4 19.38335 4.616651 .1019846 5.3201 .1057136 6.280302 |
7. | 7 15 3 15.65018 2.349822 .2069104 5.3201 .1926733 6.280302 |
8. | 8 14 0 13.08195 .9180457 .9824709 5.3201 2 6.280302 |
+------------------------------------------------------------------------------+
A simpler approach described on page 113.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
replace a = 8 if a >8
sort a
egen mwidth = mean(width), by(a)
logit y mwidth, nolog
Logit estimates Number of obs = 173
LR chi2(1) = 28.08
Prob > chi2 = 0.0000
Log likelihood = -98.84003 Pseudo R2 = 0.1244
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mwidth | .4654004 .0986921 4.72 0.000 .2719674 .6588334
_cons | -11.53299 2.552684 -4.52 0.000 -16.53616 -6.529821
------------------------------------------------------------------------------
* Stata 8 code
lfit
* Stata 9 code and output.
estat gof
Logistic model for y, goodness-of-fit test
number of observations = 173
number of covariate patterns = 8
Pearson chi2(6) = 5.02
Prob > chi2 = 0.5417
Model on ungrouped data:
logit y width, nolog
Logit estimates Number of obs = 173
LR chi2(1) = 31.31
Prob > chi2 = 0.0000
Log likelihood = -97.226331 Pseudo R2 = 0.1387
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .4972306 .1017361 4.89 0.000 .2978316 .6966297
_cons | -12.35082 2.628731 -4.70 0.000 -17.50304 -7.1986
------------------------------------------------------------------------------
* Stata 8 code.
lfit, group(10) table
* Stata 9 code and output.
estat gof, group(10) table
Logistic model for y, goodness-of-fit test
(Table collapsed on quantiles of estimated probabilities)
+--------------------------------------------------------+
| Group | Prob | Obs_1 | Exp_1 | Obs_0 | Exp_0 | Total |
|-------+--------+-------+-------+-------+-------+-------|
| 1 | 0.3621 | 5 | 5.4 | 14 | 13.6 | 19 |
| 2 | 0.4579 | 8 | 7.6 | 10 | 10.4 | 18 |
| 3 | 0.5200 | 10 | 7.6 | 5 | 7.4 | 15 |
| 4 | 0.6054 | 9 | 11.0 | 10 | 8.0 | 19 |
| 5 | 0.6518 | 11 | 10.1 | 5 | 5.9 | 16 |
|-------+--------+-------+-------+-------+-------+-------|
| 6 | 0.7161 | 11 | 12.3 | 7 | 5.7 | 18 |
| 7 | 0.7897 | 16 | 16.8 | 6 | 5.2 | 22 |
| 8 | 0.8417 | 12 | 11.5 | 2 | 2.5 | 14 |
| 9 | 0.8878 | 15 | 15.7 | 3 | 2.3 | 18 |
| 10 | 0.9867 | 14 | 13.1 | 0 | 0.9 | 14 |
+--------------------------------------------------------+
number of observations = 173
number of groups = 10
Hosmer-Lemeshow chi2(8) = 4.63
Prob > chi2 = 0.7963
Section 5.3.2, page 114-115. Goodness of fit and likelihood-ratio model comparison tests:
logit y mwidth, nolog
Logit estimates Number of obs = 173
LR chi2(1) = 28.08
Prob > chi2 = 0.0000
Log likelihood = -98.84003 Pseudo R2 = 0.1244
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mwidth | .4654004 .0986921 4.72 0.000 .2719674 .6588334
_cons | -11.53299 2.552684 -4.52 0.000 -16.53616 -6.529821
------------------------------------------------------------------------------
fitstat
Measures of Fit for logit of y
Log-Lik Intercept Only: -112.879 Log-Lik Full Model: -98.840
D(171): 197.680 LR(1): 28.078
Prob > LR: 0.000
McFadden's R2: 0.124 McFadden's Adj R2: 0.107
Maximum Likelihood R2: 0.150 Cragg & Uhler's R2: 0.206
McKelvey and Zavoina's R2: 0.219 Efron's R2: 0.145
Variance of y*: 4.212 Variance of error: 3.290
Count R2: 0.665 Adj Count R2: 0.065
AIC: 1.166 AIC*n: 201.680
BIC: -683.533 BIC': -22.925
Section 5.3.3 on residuals for logit models.
Table 5.3, page 116.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
replace a = 8 if a >8
sort a
logit y
predict pind
egen mwidth = mean(width), by(a)
logit y mwidth, nolog
predict p
predict r, residuals
predict h, hat
gen aresid = r/sqrt(1-h)
collapse (mean) mwidth r aresid pi=pind (sum) y p pind (count) n, by(a)
gen rr= (y-pi*n)/sqrt(n*pi*(1-pi))
list mwidth n y pind rr p r aresid
+------------------------------------------------------------------------------+
| mwidth n y pind rr p r aresid |
|------------------------------------------------------------------------------|
1. | 22.69286 14 5 8.982659 -2.219718 3.843518 .6925753 .8564039 |
2. | 23.84286 14 4 8.982659 -2.777064 5.496007 -.8187712 -.9297187 |
3. | 24.775 28 17 17.96532 -.3804346 13.98114 1.141024 1.344962 |
4. | 25.83846 39 21 25.02312 -1.343444 24.20473 -1.057578 -1.240055 |
5. | 26.79091 22 15 14.11561 .3932084 15.80022 -.3792292 -.4173211 |
|------------------------------------------------------------------------------|
6. | 27.7375 24 20 15.39884 1.95862 19.16056 .4270666 .4948038 |
7. | 28.66667 18 15 11.54913 1.696214 15.46522 -.3152464 -.3611885 |
8. | 30.40714 14 14 8.982659 2.796394 13.0486 1.010328 1.136103 |
+------------------------------------------------------------------------------+
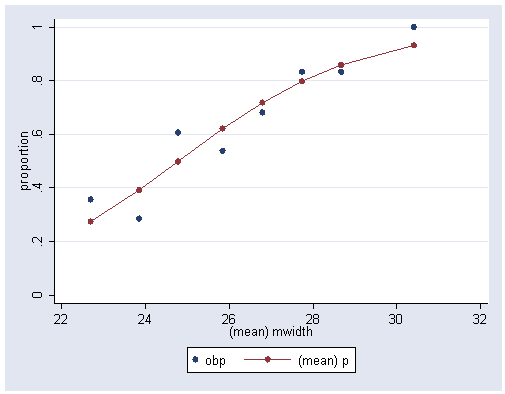
Figure 5.3, page 116.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
replace a = 8 if a >8
sort a
egen mwidth = mean(width), by(a)
logit y mwidth, nolog
predict p
collapse (mean) mwidth phat=p (sum) y p (count) n, by(a)
gen obp=y/n
graph twoway (scatter obp mwidth) (scatter phat mwidth, connect(l)), ///
ylabel(0(.2)1) xlabel(22(2)32) ytitle("proportion")
Section 5.3.4 on diagnostic measures of influence.
Table 5.4 on page 118. For the model with the variable width as a predictor, we will use ungrouped data because it is easier to generate all the diagnostic statistics using the logit command. For the model with no predictors, we will have to group the data and use the glm command. Some further calculation is needed for creating the diagnostic statistics. The details are shown below.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
gen a = ceil(width - 23.25) + 1
replace a = 1 if a<=0
replace a = 8 if a >8
sort a
egen mwidth = mean(width), by(a)
logit y mwidth, nolog
predict db, db
predict dx, dx
predict dd, dd
collapse (mean) width db dd dx (sum) y n , by(a)
glm y, fam(bin n)
Generalized linear models No. of obs = 8
Optimization : ML: Newton-Raphson Residual df = 7
Scale parameter = 1
Deviance = 34.03404409 (1/df) Deviance = 4.862006
Pearson = 29.27657443 (1/df) Pearson = 4.182368
Variance function: V(u) = u*(1-u/n) [Binomial]
Link function : g(u) = ln(u/(n-u)) [Logit]
Standard errors : OIM
Log likelihood = -28.60784483 AIC = 7.401961
BIC = 19.4779533
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | .5823958 .1585498 3.67 0.000 .2716439 .8931477
------------------------------------------------------------------------------
predict din, d
predict h2, h
predict res, p
gen x2=res^2/(1-h2)
gen din2=din^2/(1-h2)
drop din h2 res
list width db dx dd x2 din2
+-----------------------------------------------------------------+
| width db dx dd x2 din2 |
|-----------------------------------------------------------------|
1. | 22.69286 .3880239 .7334276 .6949906 5.360987 5.06951 |
2. | 23.84286 .2501259 .8643769 .9014844 8.391136 7.966363 |
3. | 24.775 .7044131 1.808922 1.822847 .1726785 .1704266 |
4. | 25.83846 .5764279 1.537736 1.503042 2.330132 2.253074 |
5. | 26.79091 .0367436 .1741569 .1699482 .1771392 .1803587 |
|-----------------------------------------------------------------|
6. | 27.7375 .0838247 .2448309 .2565225 4.454101 5.030672 |
7. | 28.66667 .0407948 .1304572 .1243544 3.211263 3.626952 |
8. | 30.40714 .3413671 1.29073 2.491689 8.508358 13.51937 |
+-----------------------------------------------------------------+
Section 5.4 Logit Models for Qualitative Predictors
Table 5.5 on page 119 and model (5.4.1).
use https://stats.idre.ucla.edu/stat/stata/examples/icda/azt, clear
list
+----------------------------+
| race azt symp count |
|----------------------------|
1. | white yes yes 14 |
2. | white yes no 93 |
3. | white no yes 32 |
4. | white no no 81 |
5. | black yes yes 11 |
|----------------------------|
6. | black yes no 52 |
7. | black no yes 12 |
8. | black no no 43 |
+----------------------------+
logit symp race azt [fw=count], nolog
Logit estimates Number of obs = 338
LR chi2(2) = 6.97
Prob > chi2 = 0.0307
Log likelihood = -167.57559 Pseudo R2 = 0.0204
------------------------------------------------------------------------------
symp | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
race | .0554845 .2886132 0.19 0.848 -.5101869 .621156
azt | -.7194599 .2789791 -2.58 0.010 -1.266249 -.1726709
_cons | -1.073574 .2629407 -4.08 0.000 -1.588928 -.5582193
------------------------------------------------------------------------------
test azt
( 1) azt = 0
chi2( 1) = 6.65
Prob > chi2 = 0.0099
* Stata 8 code.
lfit
* Stata 9 code and output.
estat gof
Logistic model for symp, goodness-of-fit test
number of observations = 338
number of covariate patterns = 4
Pearson chi2(1) = 1.39
Prob > chi2 = 0.2382
Table 5.6 on page 121. We make use of the xi3 command written by Michael Mitchell. The command xi3 is a generalization of Stata’s command xi. It allows 3 way interactions and performs additional coding schemes beyond indicator coding. You can download the xi3 program from the internet within Stata by issuing search xi3 command and then following the link (see How can I use the search command to search for programs and get additional help? for more information about using search).
xi3: logit symp i.race i.azt [fw=count], nolog
i.race _Irace_0-1 (naturally coded; _Irace_0 omitted)
i.azt _Iazt_0-1 (naturally coded; _Iazt_0 omitted)
Logit estimates Number of obs = 338
LR chi2(2) = 6.97
Prob > chi2 = 0.0307
Log likelihood = -167.57559 Pseudo R2 = 0.0204
------------------------------------------------------------------------------
symp | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Irace_1 | .0554845 .2886132 0.19 0.848 -.5101869 .621156
_Iazt_1 | -.7194599 .2789791 -2.58 0.010 -1.266249 -.1726709
_cons | -1.073574 .2629407 -4.08 0.000 -1.588928 -.5582193
------------------------------------------------------------------------------
char azt[omit] 1
char race[omit] 1
xi3: logit symp i.race i.azt [fw=count], nolog
i.race _Irace_0-1 (naturally coded; _Irace_1 omitted)
i.azt _Iazt_0-1 (naturally coded; _Iazt_1 omitted)
Logit estimates Number of obs = 338
LR chi2(2) = 6.97
Prob > chi2 = 0.0307
Log likelihood = -167.57559 Pseudo R2 = 0.0204
------------------------------------------------------------------------------
symp | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Irace_0 | -.0554845 .2886132 -0.19 0.848 -.621156 .5101869
_Iazt_0 | .7194599 .2789791 2.58 0.010 .1726709 1.266249
_cons | -1.737549 .2403847 -7.23 0.000 -2.208694 -1.266404
------------------------------------------------------------------------------
xi3: logit symp e.race e.azt [fw=count], nolog
e.race _Irace_0-1 (naturally coded; _Irace_0 omitted)
e.azt _Iazt_0-1 (naturally coded; _Iazt_0 omitted)
Logit estimates Number of obs = 338
LR chi2(2) = 6.97
Prob > chi2 = 0.0307
Log likelihood = -167.57559 Pseudo R2 = 0.0204
------------------------------------------------------------------------------
symp | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Irace_1 | .0277423 .1443066 0.19 0.848 -.2550935 .310578
_Iazt_1 | -.35973 .1394895 -2.58 0.010 -.6331244 -.0863355
_cons | -1.405561 .1466849 -9.58 0.000 -1.693059 -1.118064
------------------------------------------------------------------------------
Section 5.5.1, page 122-124. Horseshoe crab example using color and width predictors
use https://stats.idre.ucla.edu/stat/stata/examples/icda/crab, clear
char color[omit] 4
xi3: logit y i.color width
i.color _Icolor_1-4 (naturally coded; _Icolor_4 omitted)
Logit estimates Number of obs = 173
LR chi2(4) = 38.30
Prob > chi2 = 0.0000
Log likelihood = -93.728515 Pseudo R2 = 0.1697
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icolor_1 | 1.329919 .8525264 1.56 0.119 -.3410018 3.00084
_Icolor_2 | 1.402336 .5484409 2.56 0.011 .3274116 2.477261
_Icolor_3 | 1.106121 .5920835 1.87 0.062 -.0543408 2.266584
width | .467956 .1055464 4.43 0.000 .2610889 .6748231
_cons | -12.71511 2.761775 -4.60 0.000 -18.12809 -7.302133
------------------------------------------------------------------------------
prvalue , x(_Icolor_1=1 _Icolor_2=0 _Icolor_3=0)
logit: Predictions for y
Pr(y=1|x): 0.7153 95% ci: (0.3916,0.9075)
Pr(y=0|x): 0.2847 95% ci: (0.0925,0.6084)
_Icolor_1 _Icolor_2 _Icolor_3 width
x= 1 0 0 26.298844
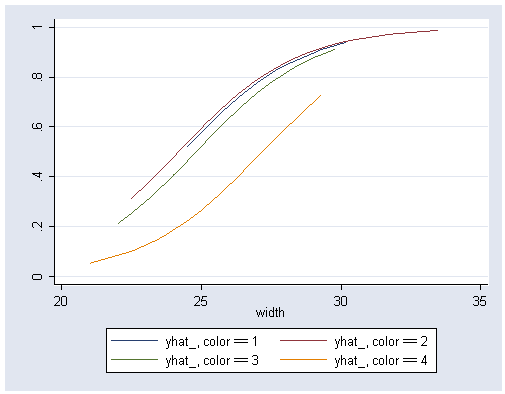
Figure 5.4 on page 124. This graph can be easily produced using the Stata program postgr3 written by Michael Mitchell. You can download the program through the internet (see How can I use the search command to search for programs and get additional help? for more information about using search).
postgr3 width, by(color) ytitle(" ")
Section 5.5.2, page 124-125. Model comparison.
logit y width
Logit estimates Number of obs = 173
LR chi2(1) = 31.31
Prob > chi2 = 0.0000
Log likelihood = -97.226331 Pseudo R2 = 0.1387
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .4972306 .1017361 4.89 0.000 .2978316 .6966297
_cons | -12.35082 2.628731 -4.70 0.000 -17.50304 -7.1986
------------------------------------------------------------------------------
lrtest, saving(m0)
xi3: logit y width i.color
i.color _Icolor_1-4 (naturally coded; _Icolor_4 omitted)
Logit estimates Number of obs = 173
LR chi2(4) = 38.30
Prob > chi2 = 0.0000
Log likelihood = -93.728515 Pseudo R2 = 0.1697
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .467956 .1055464 4.43 0.000 .2610889 .6748231
_Icolor_1 | 1.329919 .8525264 1.56 0.119 -.3410018 3.00084
_Icolor_2 | 1.402336 .5484409 2.56 0.011 .3274116 2.477261
_Icolor_3 | 1.106121 .5920835 1.87 0.062 -.0543408 2.266584
_cons | -12.71511 2.761775 -4.60 0.000 -18.12809 -7.302133
------------------------------------------------------------------------------
lrtest, using(m0)
likelihood-ratio test LR chi2(3) = 7.00
(Assumption: LRTEST_m0 nested in .) Prob > chi2 = 0.0720
Section 5.5.3, page 125-126. Quantitative treatment of ordinal predictor.
logit y width color
Logit estimates Number of obs = 173
LR chi2(2) = 36.64
Prob > chi2 = 0.0000
Log likelihood = -94.560587 Pseudo R2 = 0.1623
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .4583098 .1040194 4.41 0.000 .2544355 .662184
color | -.5090467 .2236827 -2.28 0.023 -.9474568 -.0706366
_cons | -10.07084 2.806862 -3.59 0.000 -15.57219 -4.569491
------------------------------------------------------------------------------
fitstat, saving(m0)
Measures of Fit for logit of y
Log-Lik Intercept Only: -112.879 Log-Lik Full Model: -94.561
D(170): 189.121 LR(2): 36.637
Prob > LR: 0.000
McFadden's R2: 0.162 McFadden's Adj R2: 0.136
Maximum Likelihood R2: 0.191 Cragg & Uhler's R2: 0.262
McKelvey and Zavoina's R2: 0.285 Efron's R2: 0.198
Variance of y*: 4.599 Variance of error: 3.290
Count R2: 0.728 Adj Count R2: 0.242
AIC: 1.128 AIC*n: 195.121
BIC: -686.938 BIC': -26.331
(Indices saved in matrix fs_m0)
xi3: logit y width i.color
i.color _Icolor_1-4 (naturally coded; _Icolor_4 omitted)
Logit estimates Number of obs = 173
LR chi2(4) = 38.30
Prob > chi2 = 0.0000
Log likelihood = -93.728515 Pseudo R2 = 0.1697
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .467956 .1055464 4.43 0.000 .2610889 .6748231
_Icolor_1 | 1.329919 .8525264 1.56 0.119 -.3410018 3.00084
_Icolor_2 | 1.402336 .5484409 2.56 0.011 .3274116 2.477261
_Icolor_3 | 1.106121 .5920835 1.87 0.062 -.0543408 2.266584
_cons | -12.71511 2.761775 -4.60 0.000 -18.12809 -7.302133
------------------------------------------------------------------------------
fitstat , using(m0)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 173 173 0
Log-Lik Intercept Only: -112.879 -112.879 0.000
Log-Lik Full Model: -93.729 -94.561 0.832
D: 187.457(168) 189.121(170) 1.664(2)
LR: 38.301(4) 36.637(2) 1.664(2)
Prob > LR: 0.000 0.000 0.435
McFadden's R2: 0.170 0.162 0.007
McFadden's Adj R2: 0.125 0.136 -0.010
Maximum Likelihood R2: 0.199 0.191 0.008
Cragg & Uhler's R2: 0.272 0.262 0.011
McKelvey and Zavoina's R2: 0.297 0.285 0.012
Efron's R2: 0.204 0.198 0.007
Variance of y*: 4.677 4.599 0.078
Variance of error: 3.290 3.290 0.000
Count R2: 0.734 0.728 0.006
Adj Count R2: 0.258 0.242 0.016
AIC: 1.141 1.128 0.014
AIC*n: 197.457 195.121 2.336
BIC: -678.296 -686.938 8.642
BIC': -17.688 -26.331 8.642
Difference of 8.642 in BIC' provides strong support for saved model.
Note: p-value for difference in LR is only valid if models are nested.
Section 5.5.4, page 126-127. Model selection with several predictors
xi3: logit y width i.color i.spine weight
i.color _Icolor_1-4 (naturally coded; _Icolor_4 omitted)
i.spine _Ispine_1-3 (naturally coded; _Ispine_1 omitted)
Logit estimates Number of obs = 173
LR chi2(7) = 40.56
Prob > chi2 = 0.0000
Log likelihood = -92.600999 Pseudo R2 = 0.1796
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
width | .263128 .1953012 1.35 0.178 -.1196553 .6459114
_Icolor_1 | 1.608666 .9355408 1.72 0.086 -.2249604 3.442292
_Icolor_2 | 1.505763 .5666724 2.66 0.008 .3951059 2.616421
_Icolor_3 | 1.119802 .593296 1.89 0.059 -.0430372 2.28264
_Ispine_2 | -.0959809 .7033755 -0.14 0.891 -1.474571 1.28261
_Ispine_3 | .4002868 .502712 0.80 0.426 -.5850106 1.385584
weight | .82578 .7038361 1.17 0.241 -.5537134 2.205273
_cons | -9.673681 3.86463 -2.50 0.012 -17.24822 -2.099145
------------------------------------------------------------------------------
Section 5.5.5, page 128. Backward elimination of predictors. We will use Stata command fitstat after each model to show the deviance, the degrees of freedom, the difference of deviance between models and correlation. By definition, Efron’s R2 is simply the squared correlation.
Model 1:
quietly xi3: logit y i.color*i.spine*width
fitstat, saving(m1)
Measures of Fit for logit of y
Log-Lik Intercept Only: -111.848 Log-Lik Full Model: -85.220
D(152): 170.440 LR(19): 53.255
Prob > LR: 0.000
McFadden's R2: 0.238 McFadden's Adj R2: 0.059
Maximum Likelihood R2: 0.266 Cragg & Uhler's R2: 0.366
McKelvey and Zavoina's R2: 0.973 Efron's R2: 0.269
Variance of y*: 122.792 Variance of error: 3.290
Count R2: 0.756 Adj Count R2: 0.311
AIC: 1.223 AIC*n: 210.440
BIC: -611.979 BIC': 44.547
(Indices saved in matrix fs_m1)
di sqrt(.269)
5186521
Model 2:
quietly xi3: logit y i.c*i.spine i.c*width i.spine*width
fitstat, using(m1) saving(m2)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 172 172 0
Log-Lik Intercept Only: -111.848 -111.848 0.000
Log-Lik Full Model: -86.837 -85.220 -1.617
D: 173.674(155) 170.440(152) 3.233(3)
LR: 50.022(16) 53.255(19) 3.233(3)
Prob > LR: 0.000 0.000 0.357
McFadden's R2: 0.224 0.238 -0.014
McFadden's Adj R2: 0.072 0.059 0.012
Maximum Likelihood R2: 0.252 0.266 -0.014
Cragg & Uhler's R2: 0.347 0.366 -0.019
McKelvey and Zavoina's R2: 0.824 0.973 -0.149
Efron's R2: 0.256 0.269 -0.013
Variance of y*: 18.712 122.792 -104.080
Variance of error: 3.290 3.290 0.000
Count R2: 0.762 0.756 0.006
Adj Count R2: 0.328 0.311 0.016
AIC: 1.207 1.223 -0.016
AIC*n: 207.674 210.440 -2.767
BIC: -624.188 -611.979 -12.209
BIC': 32.338 44.547 -12.209
Difference of 12.209 in BIC' provides very strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
(Indices saved in matrix fs_m2)
Model 3a:
quietly xi3: logit y i.c*i.spine i.spine*width
fitstat, using(m2)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 172 172 0
Log-Lik Intercept Only: -111.848 -111.848 0.000
Log-Lik Full Model: -88.668 -86.837 -1.831
D: 177.336(158) 173.674(155) 3.662(3)
LR: 46.360(13) 50.022(16) 3.662(3)
Prob > LR: 0.000 0.000 0.300
McFadden's R2: 0.207 0.224 -0.016
McFadden's Adj R2: 0.082 0.072 0.010
Maximum Likelihood R2: 0.236 0.252 -0.016
Cragg & Uhler's R2: 0.325 0.347 -0.022
McKelvey and Zavoina's R2: 0.816 0.824 -0.008
Efron's R2: 0.241 0.256 -0.015
Variance of y*: 17.879 18.712 -0.834
Variance of error: 3.290 3.290 0.000
Count R2: 0.733 0.762 -0.029
Adj Count R2: 0.246 0.328 -0.082
AIC: 1.194 1.207 -0.014
AIC*n: 205.336 207.674 -2.338
BIC: -635.968 -624.188 -11.780
BIC': 20.557 32.338 -11.780
Difference of 11.780 in BIC' provides very strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
Model 3b:
quietly xi3: logit y i.c*width i.spine*width
fitstat, using(m2) force
Measures of Fit for logit of y
Warning: N's do not match.
Current Saved Difference
Model: logit logit
N: 173 172 1
Log-Lik Intercept Only: -112.879 -111.848 -1.031
Log-Lik Full Model: -90.779 -86.837 -3.943
D: 181.559(161) 173.674(155) 7.885(6)
LR: 44.200(11) 50.022(16) 5.822(5)
Prob > LR: 0.000 0.000 0.324
McFadden's R2: 0.196 0.224 -0.028
McFadden's Adj R2: 0.089 0.072 0.018
Maximum Likelihood R2: 0.225 0.252 -0.027
Cragg & Uhler's R2: 0.309 0.347 -0.037
McKelvey and Zavoina's R2: 0.326 0.824 -0.498
Efron's R2: 0.231 0.256 -0.025
Variance of y*: 4.881 18.712 -13.832
Variance of error: 3.290 3.290 0.000
Count R2: 0.746 0.762 -0.016
Adj Count R2: 0.290 0.328 -0.038
AIC: 1.188 1.207 -0.019
AIC*n: 205.559 207.674 -2.115
BIC: -648.121 -624.188 -23.933
BIC': 12.487 32.338 -19.851
Note: p-value for difference in LR is only valid if models are nested.
Model 3c:
quietly xi3: logit y i.c*i.spine i.c*width
fitstat, using(m2) saving(m3c)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 172 172 0
Log-Lik Intercept Only: -111.848 -111.848 0.000
Log-Lik Full Model: -86.838 -86.837 -0.001
D: 173.676(157) 173.674(155) 0.003(2)
LR: 50.019(14) 50.022(16) 0.003(2)
Prob > LR: 0.000 0.000 0.999
McFadden's R2: 0.224 0.224 -0.000
McFadden's Adj R2: 0.089 0.072 0.018
Maximum Likelihood R2: 0.252 0.252 -0.000
Cragg & Uhler's R2: 0.347 0.347 -0.000
McKelvey and Zavoina's R2: 0.821 0.824 -0.003
Efron's R2: 0.256 0.256 -0.000
Variance of y*: 18.394 18.712 -0.318
Variance of error: 3.290 3.290 0.000
Count R2: 0.762 0.762 0.000
Adj Count R2: 0.328 0.328 0.000
AIC: 1.184 1.207 -0.023
AIC*n: 203.676 207.674 -3.997
BIC: -634.480 -624.188 -10.292
BIC': 22.046 32.338 -10.292
Difference of 10.292 in BIC' provides very strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
(Indices saved in matrix fs_m3c)
Model 4a:
quietly xi3: logit y i.spine i.c*width
fitstat, using(m3c) force
Measures of Fit for logit of y
Warning: N's do not match.
Current Saved Difference
Model: logit logit
N: 173 172 1
Log-Lik Intercept Only: -112.879 -111.848 -1.031
Log-Lik Full Model: -90.819 -86.838 -3.980
D: 181.637(163) 173.676(157) 7.961(6)
LR: 44.122(9) 50.019(14) 5.898(5)
Prob > LR: 0.000 0.000 0.316
McFadden's R2: 0.195 0.224 -0.028
McFadden's Adj R2: 0.107 0.089 0.017
Maximum Likelihood R2: 0.225 0.252 -0.027
Cragg & Uhler's R2: 0.309 0.347 -0.038
McKelvey and Zavoina's R2: 0.323 0.821 -0.498
Efron's R2: 0.231 0.256 -0.025
Variance of y*: 4.863 18.394 -13.531
Variance of error: 3.290 3.290 0.000
Count R2: 0.740 0.762 -0.022
Adj Count R2: 0.274 0.328 -0.054
AIC: 1.166 1.184 -0.019
AIC*n: 201.637 203.676 -2.039
BIC: -658.350 -634.480 -23.869
BIC': 2.258 22.046 -19.787
Note: p-value for difference in LR is only valid if models are nested.
Model 4b:
quietly xi3: logit y width i.c*i.spine
fitstat, using(m3c) saving(m4b)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 172 172 0
Log-Lik Intercept Only: -111.848 -111.848 0.000
Log-Lik Full Model: -88.798 -86.838 -1.960
D: 177.597(160) 173.676(157) 3.920(3)
LR: 46.099(11) 50.019(14) 3.920(3)
Prob > LR: 0.000 0.000 0.270
McFadden's R2: 0.206 0.224 -0.018
McFadden's Adj R2: 0.099 0.089 0.009
Maximum Likelihood R2: 0.235 0.252 -0.017
Cragg & Uhler's R2: 0.323 0.347 -0.024
McKelvey and Zavoina's R2: 0.822 0.821 0.001
Efron's R2: 0.240 0.256 -0.016
Variance of y*: 18.485 18.394 0.091
Variance of error: 3.290 3.290 0.000
Count R2: 0.738 0.762 -0.023
Adj Count R2: 0.262 0.328 -0.066
AIC: 1.172 1.184 -0.012
AIC*n: 201.597 203.676 -2.080
BIC: -646.002 -634.480 -11.522
BIC': 10.523 22.046 -11.522
Difference of 11.522 in BIC' provides very strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
(Indices saved in matrix fs_m4b)
Model 5:
quietly xi3: logit y i.color i.spine width
fitstat, using(m4c) saving(m5) force
Measures of Fit for logit of y
Warning: N's do not match.
Current Saved Difference
Model: logit logit
N: 173 172 1
Log-Lik Intercept Only: -112.879 -111.848 -1.031
Log-Lik Full Model: -93.306 -88.798 -4.508
D: 186.612(166) 177.597(160) 9.015(6)
LR: 39.147(6) 46.099(11) 6.953(5)
Prob > LR: 0.000 0.000 0.224
McFadden's R2: 0.173 0.206 -0.033
McFadden's Adj R2: 0.111 0.099 0.013
Maximum Likelihood R2: 0.203 0.235 -0.033
Cragg & Uhler's R2: 0.278 0.323 -0.045
McKelvey and Zavoina's R2: 0.298 0.822 -0.524
Efron's R2: 0.208 0.240 -0.032
Variance of y*: 4.689 18.485 -13.796
Variance of error: 3.290 3.290 0.000
Count R2: 0.740 0.738 0.002
Adj Count R2: 0.274 0.262 0.012
AIC: 1.160 1.172 -0.012
AIC*n: 200.612 201.597 -0.985
BIC: -668.835 -646.002 -22.832
BIC': -8.227 10.523 -18.750
Note: p-value for difference in LR is only valid if models are nested.
(Indices saved in matrix fs_m5)
Model 6a:
quietly xi3: logit y i.color i.spine
fitstat, using(m5)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 173 173 0
Log-Lik Intercept Only: -112.879 -112.879 0.000
Log-Lik Full Model: -104.417 -93.306 -11.111
D: 208.834(167) 186.612(166) 22.222(1)
LR: 16.925(5) 39.147(6) 22.222(1)
Prob > LR: 0.005 0.000 0.000
McFadden's R2: 0.075 0.173 -0.098
McFadden's Adj R2: 0.022 0.111 -0.090
Maximum Likelihood R2: 0.093 0.203 -0.109
Cragg & Uhler's R2: 0.128 0.278 -0.150
McKelvey and Zavoina's R2: 0.118 0.298 -0.180
Efron's R2: 0.099 0.208 -0.109
Variance of y*: 3.731 4.689 -0.958
Variance of error: 3.290 3.290 0.000
Count R2: 0.688 0.740 -0.052
Adj Count R2: 0.129 0.274 -0.145
AIC: 1.276 1.160 0.117
AIC*n: 220.834 200.612 20.222
BIC: -651.766 -668.835 17.069
BIC': 8.842 -8.227 17.069
Difference of 17.069 in BIC' provides very strong support for saved model.
Note: p-value for difference in LR is only valid if models are nested.
Model 6b:
quietly xi3: logit y i.spine width
fitstat, using(m5)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 173 173 0
Log-Lik Intercept Only: -112.879 -112.879 0.000
Log-Lik Full Model: -97.212 -93.306 -3.906
D: 194.425(169) 186.612(166) 7.813(3)
LR: 31.334(3) 39.147(6) 7.813(3)
Prob > LR: 0.000 0.000 0.050
McFadden's R2: 0.139 0.173 -0.035
McFadden's Adj R2: 0.103 0.111 -0.008
Maximum Likelihood R2: 0.166 0.203 -0.037
Cragg & Uhler's R2: 0.227 0.278 -0.051
McKelvey and Zavoina's R2: 0.250 0.298 -0.048
Efron's R2: 0.161 0.208 -0.046
Variance of y*: 4.386 4.689 -0.303
Variance of error: 3.290 3.290 0.000
Count R2: 0.705 0.740 -0.035
Adj Count R2: 0.177 0.274 -0.097
AIC: 1.170 1.160 0.010
AIC*n: 202.425 200.612 1.813
BIC: -676.481 -668.835 -7.647
BIC': -15.874 -8.227 -7.647
Difference of 7.647 in BIC' provides strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
Model 6c:
quietly xi3: logit y i.color width
fitstat, using(m5) saving(m6c)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 173 173 0
Log-Lik Intercept Only: -112.879 -112.879 0.000
Log-Lik Full Model: -93.729 -93.306 -0.423
D: 187.457(168) 186.612(166) 0.845(2)
LR: 38.301(4) 39.147(6) 0.845(2)
Prob > LR: 0.000 0.000 0.655
McFadden's R2: 0.170 0.173 -0.004
McFadden's Adj R2: 0.125 0.111 0.014
Maximum Likelihood R2: 0.199 0.203 -0.004
Cragg & Uhler's R2: 0.272 0.278 -0.005
McKelvey and Zavoina's R2: 0.297 0.298 -0.002
Efron's R2: 0.204 0.208 -0.003
Variance of y*: 4.677 4.689 -0.011
Variance of error: 3.290 3.290 0.000
Count R2: 0.734 0.740 -0.006
Adj Count R2: 0.258 0.274 -0.016
AIC: 1.141 1.160 -0.018
AIC*n: 197.457 200.612 -3.155
BIC: -678.296 -668.835 -9.461
BIC': -17.688 -8.227 -9.461
Difference of 9.461 in BIC' provides strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
(Indices saved in matrix fs_m6c)
di sqrt(.204)
.45166359
Model 7a:
quietly xi3: logit y i.color
fitstat, using(m6c)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 173 173 0
Log-Lik Intercept Only: -112.879 -112.879 0.000
Log-Lik Full Model: -106.030 -93.729 -12.302
D: 212.061(169) 187.457(168) 24.604(1)
LR: 13.698(3) 38.301(4) 24.604(1)
Prob > LR: 0.003 0.000 0.000
McFadden's R2: 0.061 0.170 -0.109
McFadden's Adj R2: 0.025 0.125 -0.100
Maximum Likelihood R2: 0.076 0.199 -0.122
Cragg & Uhler's R2: 0.104 0.272 -0.168
McKelvey and Zavoina's R2: 0.095 0.297 -0.201
Efron's R2: 0.081 0.204 -0.123
Variance of y*: 3.636 4.677 -1.041
Variance of error: 3.290 3.290 0.000
Count R2: 0.688 0.734 -0.046
Adj Count R2: 0.129 0.258 -0.129
AIC: 1.272 1.141 0.131
AIC*n: 220.061 197.457 22.604
BIC: -658.845 -678.296 19.451
BIC': 1.762 -17.688 19.451
Difference of 19.451 in BIC' provides very strong support for saved model.
Note: p-value for difference in LR is only valid if models are nested.
di sqrt(.081)
.28460499
Model 7b:
quietly logit y width
fitstat, using(m6c)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 173 173 0
Log-Lik Intercept Only: -112.879 -112.879 0.000
Log-Lik Full Model: -97.226 -93.729 -3.498
D: 194.453(171) 187.457(168) 6.996(3)
LR: 31.306(1) 38.301(4) 6.996(3)
Prob > LR: 0.000 0.000 0.072
McFadden's R2: 0.139 0.170 -0.031
McFadden's Adj R2: 0.121 0.125 -0.004
Maximum Likelihood R2: 0.166 0.199 -0.033
Cragg & Uhler's R2: 0.227 0.272 -0.045
McKelvey and Zavoina's R2: 0.251 0.297 -0.046
Efron's R2: 0.161 0.204 -0.043
Variance of y*: 4.390 4.677 -0.288
Variance of error: 3.290 3.290 0.000
Count R2: 0.705 0.734 -0.029
Adj Count R2: 0.177 0.258 -0.081
AIC: 1.147 1.141 0.006
AIC*n: 198.453 197.457 0.996
BIC: -686.760 -678.296 -8.464
BIC': -26.153 -17.688 -8.464
Difference of 8.464 in BIC' provides strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
di sqrt(.161)
.40124805
Model 8:
gen cdark = color==4
quietly logit y width cdark
fitstat, using(m6c) saving(m8)
Measures of Fit for logit of y
Current Saved Difference
Model: logit logit
N: 173 173 0
Log-Lik Intercept Only: -112.879 -112.879 0.000
Log-Lik Full Model: -93.979 -93.729 -0.250
D: 187.958(170) 187.457(168) 0.501(2)
LR: 37.801(2) 38.301(4) 0.501(2)
Prob > LR: 0.000 0.000 0.778
McFadden's R2: 0.167 0.170 -0.002
McFadden's Adj R2: 0.141 0.125 0.015
Maximum Likelihood R2: 0.196 0.199 -0.002
Cragg & Uhler's R2: 0.269 0.272 -0.003
McKelvey and Zavoina's R2: 0.294 0.297 -0.003
Efron's R2: 0.200 0.204 -0.005
Variance of y*: 4.658 4.677 -0.020
Variance of error: 3.290 3.290 0.000
Count R2: 0.728 0.734 -0.006
Adj Count R2: 0.242 0.258 -0.016
AIC: 1.121 1.141 -0.020
AIC*n: 193.958 197.457 -3.499
BIC: -688.102 -678.296 -9.806
BIC': -27.494 -17.688 -9.806
Difference of 9.806 in BIC' provides strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
di sqrt(.200) .4472136
Model 9:
quietly glm y, fam(bin) di e(deviance) - 187.96 37.798523
Section 5.6.1, page 130. Sample Size for Comparing Two Proportions
We also showed Stata command sampsi which yields similar answer.
di (invnorm(.975)+invnorm(.9))^2*(.2*.8+.3*.7)/(.2-.3)^2
388.77465
sampsi .2 .3
Estimated sample size for two-sample comparison of proportions
Test Ho: p1 = p2, where p1 is the proportion in population 1
and p2 is the proportion in population 2
Assumptions:
alpha = 0.0500 (two-sided)
power = 0.9000
p1 = 0.2000
p2 = 0.3000
n2/n1 = 1.00
Estimated required sample sizes:
n1 = 412
n2 = 412