Table 8.2 on page 207.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/gator, clear
* Stata 8 code.
mlogit c length, basecategory(3) nolog
* Stata 9 code and output.
mlogit c length, baseoutcome(3) nolog
Multinomial logistic regression Number of obs = 59
LR chi2(2) = 16.80
Prob > chi2 = 0.0002
Log likelihood = -49.170622 Pseudo R2 = 0.1459
------------------------------------------------------------------------------
c | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
F |
length | -.110109 .517082 -0.21 0.831 -1.123571 .9033531
_cons | 1.617731 1.307275 1.24 0.216 -.9444801 4.179943
-------------+----------------------------------------------------------------
I |
length | -2.465446 .8996502 -2.74 0.006 -4.228728 -.7021643
_cons | 5.697444 1.793808 3.18 0.001 2.181644 9.213244
------------------------------------------------------------------------------
(Outcome c==O is the comparison group)
test length
( 1) [F]length = 0
( 2) [I]length = 0
chi2( 2) = 8.94
Prob > chi2 = 0.0115
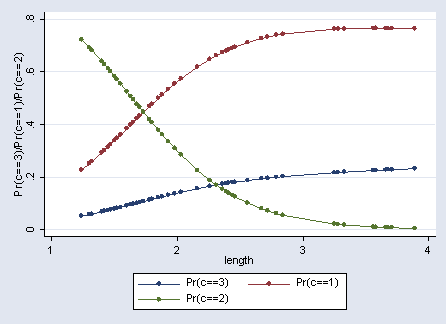
Figure 8.1 on page 209.
predict po, o(3) (option p assumed; predicted probability) predict pf, o(1) (option p assumed; predicted probability) predict pi, o(2) (option p assumed; predicted probability) graph twoway connected po pf pi length
Table 8.3 and Table 8.4 on page 210.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/belief, clear
* Stata 8 code.
xi: mlogit belief i.female i.race [fw=count], basecategory(3) nolog
* Stata 9 code and output.
xi: mlogit belief i.female i.race [fw=count], baseoutcome(3) nolog
i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted)
i.race _Irace_0-1 (naturally coded; _Irace_0 omitted)
Multinomial logistic regression Number of obs = 991
LR chi2(4) = 8.74
Prob > chi2 = 0.0678
Log likelihood = -773.72651 Pseudo R2 = 0.0056
------------------------------------------------------------------------------
belief | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yes |
_Ifemale_1 | .4185504 .171255 2.44 0.015 .0828967 .7542041
_Irace_1 | .3417744 .2370375 1.44 0.149 -.1228107 .8063594
_cons | .8830521 .2426433 3.64 0.000 .40748 1.358624
-------------+----------------------------------------------------------------
Undecided |
_Ifemale_1 | .1050638 .2465096 0.43 0.670 -.3780861 .5882137
_Irace_1 | .2709752 .3541269 0.77 0.444 -.4231007 .9650512
_cons | -.7580088 .3613564 -2.10 0.036 -1.466254 -.0497633
------------------------------------------------------------------------------
(Outcome belief==No is the comparison group)
test _Ifemale_1
( 1) [yes]_Ifemale_1 = 0
( 2) [Undecided]_Ifemale_1 = 0
chi2( 2) = 7.21
Prob > chi2 = 0.0272
predict p1, o(1)
(option p assumed; predicted probability)
predict p2, o(2)
(option p assumed; predicted probability)
predict p3, o(3)
(option p assumed; predicted probability)
gen c1 = count*p1
gen c2=count*p2
gen c3=count*p3
* Stata 8 code.
egen t1=sum(c1), by(race female)
egen t2=sum(c2), by(race female)
egen t3=sum(c3), by(race female
* Stata 9 code.
egen t1=total(c1), by(race female)
egen t2=total(c2), by(race female)
egen t3=total(c3), by(race female
gen t = (belief==1)*t1 + (belief==2)*t2 + (belief==3)*t3
table race belief female, c(mean count mean t)
------------------------------------------------------------------------------
| female and belief
| -------------- 0 -------------- -------------- 1 --------------
race | yes Undecided No yes Undecided No
----------+-------------------------------------------------------------------
0 | 25 5 13 64 9 15
| 26.75305 5.184056 11.06289 62.24695 8.815945 16.93711
|
1 | 250 45 71 371 49 74
| 248.2469 44.81594 72.93711 372.7531 49.18406 72.0629
------------------------------------------------------------------------------
Table 8.5 on page 211.
tablist race female p1 p2 p3 +-------------------------------------------------------+ | race female p1 p2 p3 Freq | |-------------------------------------------------------| | 0 0 .622164 .1205594 .2572766 3 | | 0 1 .7073517 .1001812 .1924671 3 | | 1 0 .6782703 .1224479 .1992817 3 | | 1 1 .7545608 .0995629 .1458763 3 | +-------------------------------------------------------+
Section 8.2.2, political ideology example on page 214.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/ideology, clear
xi: ologit poli i.party [fw=count]
i.party _Iparty_0-1 (naturally coded; _Iparty_0 omitted)
Ordered logit estimates Number of obs = 835
LR chi2(1) = 58.65
Prob > chi2 = 0.0000
Log likelihood = -1237.4925 Pseudo R2 = 0.0231
------------------------------------------------------------------------------
poli | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iparty_1 | -.9745155 .1291641 -7.54 0.000 -1.227673 -.7213584
-------------+----------------------------------------------------------------
_cut1 | -2.468992 .1317757 (Ancillary parameters)
_cut2 | -1.474543 .1089724
_cut3 | .2371247 .0942278
_cut4 | 1.069538 .1039157
------------------------------------------------------------------------------
predict p1, o(1)
predict p2, o(2)
predict p3, o(3)
predict p4, o(4)
predict p5, o(5)
gen c1 = count*p1
gen c2 = count*p2
gen c3 = count*p3
gen c4 = count*p4
gen c5 = count*p5
* Stata 8 code.
egen t1=sum(c1), by(party)
egen t2=sum(c2), by(party)
egen t3=sum(c3), by(party)
egen t4=sum(c4), by(party)
egen t5=sum(c5), by(party)
* Stata 9 code.
egen t1=total(c1), by(party)
egen t2=total(c2), by(party)
egen t3=total(c3), by(party)
egen t4=total(c4), by(party)
egen t5=total(c5), by(party)
gen t = (poli==1)*t1 + (poli==2)*t2 + (poli==3)*t3+(poli==4)*t4 +(poli==5)*t5
table poli party, c(mean count mean t)
------------------------------------------
| party
poli | 0 1
----------------------+-------------------
Very Liberal | 30 80
| 31.77072 78.43132
|
Slightly Liberal | 46 81
| 44.03427 83.15329
|
Moderate | 148 171
| 151.71 168.2275
|
Slightly Conservative | 84 41
| 75.50014 49.1157
|
Very Conservative | 99 55
| 103.9848 49.07219
------------------------------------------
Calculation on page 215 comparing ologit model with mlogit model.
The fitstat command needs to be downloaded prior to its use, which can be done by typing search fitstat in the command line (see How can I use the search command to search for programs and get additional help? for more information about using search).
quietly xi: mlogit poli i.party [fw=count]
fitstat, saving(m0)
Measures of Fit for mlogit of poli
Log-Lik Intercept Only: -1266.815 Log-Lik Full Model: -1235.649
D(827): 2471.297 LR(4): 62.333
Prob > LR: 0.000
McFadden's R2: 0.025 McFadden's Adj R2: 0.018
Maximum Likelihood R2: 0.072 Cragg & Uhler's R2: 0.076
Count R2: 0.382 Adj Count R2: 0.000
AIC: 2.979 AIC*n: 2487.297
BIC: -3092.289 BIC': -35.423
(Indices saved in matrix fs_m0)
quietly xi: ologit poli i.party [fw=count]
fitstat, using(m0) force
Measures of Fit for ologit of poli
Warning: Current model estimated by ologit, but saved model estimated by mlogit
Current Saved Difference
Model: ologit mlogit
N: 835 835 0
Log-Lik Intercept Only: -1266.815 -1266.815 0.000
Log-Lik Full Model: -1237.492 -1235.649 -1.844
D: 2474.985(830) 2471.297(827) 3.688(3)
LR: 58.645(1) 62.333(4) 3.688(3)
Prob > LR: 0.000 0.000 0.297
McFadden's R2: 0.023 0.025 -0.001
McFadden's Adj R2: 0.019 0.018 0.001
Maximum Likelihood R2: 0.068 0.072 -0.004
Cragg & Uhler's R2: 0.071 0.076 -0.004
McKelvey and Zavoina's R2: 0.067 . .
Variance of y*: 3.527 . .
Variance of error: 3.290 . .
Count R2: 0.382 0.382 0.000
Adj Count R2: 0.000 0.000 0.000
AIC: 2.976 2.979 -0.003
AIC*n: 2484.985 2487.297 -2.312
BIC: -3108.783 -3092.289 -16.495
BIC': -51.918 -35.423 -16.495
Difference of 16.495 in BIC' provides very strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
Section 8.3.2 Political Ideology Example Revisited on page 217. Because Stata does not have a command that does adjacent-categories logits yet, we are going make use the connection of adjacent-categories logit models with loglinear models. Section 8.3.3 gives detailed discussion on the connections. The following Stata session is based on this section.
gen asso = party*poli
xi: glm count i.party i.poli asso, fam(poi) nolog
i.party _Iparty_0-1 (naturally coded; _Iparty_0 omitted)
i.poli _Ipoli_1-5 (naturally coded; _Ipoli_1 omitted)
Generalized linear models No. of obs = 10
Optimization : ML: Newton-Raphson Residual df = 3
Scale parameter = 1
Deviance = 5.523837846 (1/df) Deviance = 1.841279
Pearson = 5.43994845 (1/df) Pearson = 1.813316
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -33.41041192 AIC = 8.082082
BIC = -1.383917433
------------------------------------------------------------------------------
count | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iparty_1 | 1.4036 .2003867 7.00 0.000 1.010849 1.796351
_Ipoli_2 | .4389135 .1396153 3.14 0.002 .1652724 .7125545
_Ipoli_3 | 1.611337 .1422775 11.33 0.000 1.332478 1.890195
_Ipoli_4 | .8790819 .1749582 5.02 0.000 .5361702 1.221994
_Ipoli_5 | 1.246704 .181057 6.89 0.000 .8918388 1.601569
asso | -.4348635 .0599649 -7.25 0.000 -.5523925 -.3173345
_cons | 3.409978 .1424304 23.94 0.000 3.130819 3.689136
------------------------------------------------------------------------------
xi: poisson count i.party i.poli asso
i.party _Iparty_0-1 (naturally coded; _Iparty_0 omitted)
i.poli _Ipoli_1-5 (naturally coded; _Ipoli_1 omitted)
Poisson regression Number of obs = 10
LR chi2(6) = 211.47
Prob > chi2 = 0.0000
Log likelihood = -33.410412 Pseudo R2 = 0.7599
------------------------------------------------------------------------------
count | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iparty_1 | 1.4036 .2003867 7.00 0.000 1.010849 1.796351
_Ipoli_2 | .4389135 .1396153 3.14 0.002 .1652724 .7125545
_Ipoli_3 | 1.611337 .1422775 11.33 0.000 1.332478 1.890195
_Ipoli_4 | .8790819 .1749582 5.02 0.000 .5361702 1.221994
_Ipoli_5 | 1.246704 .181057 6.89 0.000 .8918388 1.601569
asso | -.4348635 .0599649 -7.25 0.000 -.5523925 -.3173345
_cons | 3.409978 .1424304 23.94 0.000 3.130819 3.689136
------------------------------------------------------------------------------
fitstat, saving(m0)
Measures of Fit for poisson of count
Log-Lik Intercept Only: -139.145 Log-Lik Full Model: -33.410
D(3): 66.821 LR(6): 211.468
Prob > LR: 0.000
McFadden's R2: 0.760 McFadden's Adj R2: 0.710
Maximum Likelihood R2: 1.000 Cragg & Uhler's R2: 1.000
AIC: 8.082 AIC*n: 80.821
BIC: 59.913 BIC': -197.653
(Indices saved in matrix fs_m0)
xi: poisson count i.party i.poli
i.party _Iparty_0-1 (naturally coded; _Iparty_0 omitted)
i.poli _Ipoli_1-5 (naturally coded; _Ipoli_1 omitted)
Poisson regression Number of obs = 10
LR chi2(5) = 154.66
Prob > chi2 = 0.0000
Log likelihood = -61.814888 Pseudo R2 = 0.5558
------------------------------------------------------------------------------
count | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iparty_1 | .05031 .0692348 0.73 0.467 -.0853876 .1860076
_Ipoli_2 | .1437067 .1302495 1.10 0.270 -.1115776 .398991
_Ipoli_3 | 1.064711 .1105699 9.63 0.000 .8479977 1.281424
_Ipoli_4 | .1278334 .1307322 0.98 0.328 -.128397 .3840638
_Ipoli_5 | .3364722 .1248376 2.70 0.007 .0917951 .5811494
_cons | 3.981862 .1017365 39.14 0.000 3.782462 4.181262
------------------------------------------------------------------------------
fitstat , using(m0)
Measures of Fit for poisson of count
Current Saved Difference
Model: poisson poisson
N: 10 10 0
Log-Lik Intercept Only: -139.145 -139.145 0.000
Log-Lik Full Model: -61.815 -33.410 -28.404
D: 123.630(4) 66.821(3) 56.809(1)
LR: 154.659(5) 211.468(6) 56.809(1)
Prob > LR: 0.000 0.000 0.000
McFadden's R2: 0.556 0.760 -0.204
McFadden's Adj R2: 0.513 0.710 -0.197
Maximum Likelihood R2: 1.000 1.000 -0.000
Cragg & Uhler's R2: 1.000 1.000 -0.000
AIC: 13.563 8.082 5.481
AIC*n: 135.630 80.821 54.809
BIC: 114.419 59.913 54.506
BIC': -143.147 -197.653 54.506
Difference of 54.506 in BIC' provides very strong support for saved model.
Note: p-value for difference in LR is only valid if models are nested.
Example on page 218.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/cmh, clear
egen score_inc = group(income)
egen score_sat=group(satisf)
gen as_inc_sat = score_inc*score_sat
gen as_g_sat=female*score_sat
xi: glm count i.score_inc*i.female i.score_sat as_inc_sat as_g_sat, fam(poi)
i.score_inc _Iscore_inc_1-4 (naturally coded; _Iscore_inc_1 omitted)
i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted)
i.sco~c*i.fem~e _IscoXfem_#_# (coded as above)
i.score_sat _Iscore_sat_1-4 (naturally coded; _Iscore_sat_1 omitted)
Generalized linear models No. of obs = 32
Optimization : ML: Newton-Raphson Residual df = 19
Scale parameter = 1
Deviance = 12.55018113 (1/df) Deviance = .6605358
Pearson = 13.07329031 (1/df) Pearson = .6880679
Variance function: V(u) = u [Poisson]
Link function : g(u) = ln(u) [Log]
Standard errors : OIM
Log likelihood = -44.59671644 AIC = 3.599795
BIC = -53.29880103
------------------------------------------------------------------------------
count | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iscore_in~2 | -.5201937 .6918774 -0.75 0.452 -1.876248 .8358611
_Iscore_in~3 | -1.596889 1.032245 -1.55 0.122 -3.620052 .4262743
_Iscore_in~4 | -2.372505 1.477895 -1.61 0.108 -5.269127 .5241163
_Ifemale_1 | 1.345783 1.000194 1.35 0.178 -.6145611 3.306126
_IscoXfe~2_1 | -.1927402 .6435205 -0.30 0.765 -1.454017 1.068537
_IscoXfe~3_1 | -.8700178 .6666975 -1.30 0.192 -2.176721 .4366853
_IscoXfe~4_1 | -1.892739 .6886537 -2.75 0.006 -3.242476 -.543003
_Iscore_sa~2 | .5506684 .6794667 0.81 0.418 -.781062 1.882399
_Iscore_sa~3 | 1.205675 .9563391 1.26 0.207 -.6687149 3.080066
_Iscore_sa~4 | -.8202588 1.423346 -0.58 0.564 -3.609966 1.969448
as_inc_sat | .3887574 .1546574 2.51 0.012 .0856345 .6918803
as_g_sat | -.0446941 .3144448 -0.14 0.887 -.6609945 .5716064
_cons | -1.283851 .7736723 -1.66 0.097 -2.80022 .2325194
------------------------------------------------------------------------------
Example on page 219.
use https://stats.idre.ucla.edu/stat/stata/examples/icda/mice, clear
gen res = response
replace res = 2 if response==3
(5 real changes made)
ologit res con [fw=count]
Ordered logit estimates Number of obs = 1435
LR chi2(1) = 253.33
Prob > chi2 = 0.0000
Log likelihood = -514.76863 Pseudo R2 = 0.1975
------------------------------------------------------------------------------
res | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
con | -.0063891 .0004348 -14.70 0.000 -.0072412 -.0055369
-------------+----------------------------------------------------------------
_cut1 | -3.247934 .1576601 (Ancillary parameter)
------------------------------------------------------------------------------
ologit response con [fw=count] if response ~=1
Ordered logit estimates Number of obs = 1199
LR chi2(1) = 646.52
Prob > chi2 = 0.0000
Log likelihood = -215.61852 Pseudo R2 = 0.5999
------------------------------------------------------------------------------
response | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
con | -.0173747 .0012273 -14.16 0.000 -.0197801 -.0149693
-------------+----------------------------------------------------------------
_cut1 | -5.701902 .3322419 (Ancillary parameter)
------------------------------------------------------------------------------