Use data file crac3, page 714.
use https://stats.idre.ucla.edu/stat/stata/examples/kirk/crac3, clear
sort a
by a: gen n = _n
list, clean
a y x n
1. 1 1 1 1
2. 1 1.5 2 2
3. 1 2 4 3
4. 1 1.8 3 4
5. 2 2.6 4.5 1
6. 2 2 2 2
7. 2 2.3 3 3
8. 2 2.5 4 4
9. 3 4.8 3 1
10. 3 4 2 2
11. 3 5.3 4 3
12. 3 6 5 4
Parts of Table 15.2-1, page 714.
tabdisp n a, cellvar(y)
----------+-----------------
| a
n | 1 2 3
----------+-----------------
1 | 1 2.6 4.8
2 | 1.5 2 4
3 | 2 2.3 5.3
4 | 1.8 2.5 6
----------+-----------------
tabdisp n a, cellvar(x)
----------+-----------------
| a
n | 1 2 3
----------+-----------------
1 | 1 4.5 3
2 | 2 2 2
3 | 4 3 4
4 | 3 4 5
----------+-----------------
table a, cont(mean y mean x)
----------+-----------------------
a | mean(y) mean(x)
----------+-----------------------
1 | 1.575 2.5
2 | 2.35 3.375
3 | 5.025 3.5
----------+-----------------------
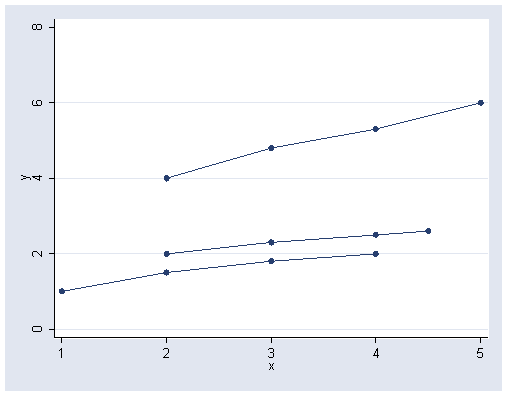
Figure 15.2-1, page 714.
Note: The sort command before the graph command is used to collect scores for each group together.
sort a x graph twoway scatter y x, connect(L) ylabel(0(2)8)
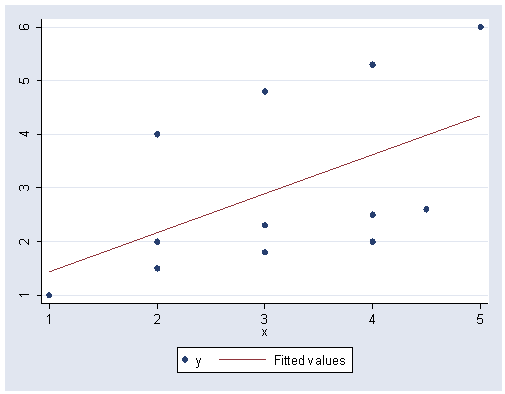
Figure 15.2-2, page 715.
graph twoway (scatter y x) (lfit y x)
Regression coefficients for each of the three groups, page 715.
regress y x if a==1
Source | SS df MS Number of obs = 4
---------+------------------------------ F( 1, 2) = 47.35
Model | .544499984 1 .544499984 Prob > F = 0.0205
Residual | .022999994 2 .011499997 R-squared = 0.9595
---------+------------------------------ Adj R-squared = 0.9392
Total | .567499979 3 .18916666 Root MSE = .10724
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | .33 .0479583 6.881 0.020 .123652 .5363479
_cons | .75 .1313392 5.710 0.029 .1848929 1.315107
------------------------------------------------------------------------------
regress y x if a==2
Source | SS df MS Number of obs = 4
---------+------------------------------ F( 1, 2) = 175.00
Model | .207627076 1 .207627076 Prob > F = 0.0057
Residual | .002372881 2 .00118644 R-squared = 0.9887
---------+------------------------------ Adj R-squared = 0.9831
Total | .209999957 3 .069999986 Root MSE = .03444
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | .2372881 .0179373 13.229 0.006 .1601102 .3144661
_cons | 1.549153 .0629405 24.613 0.002 1.278342 1.819964
------------------------------------------------------------------------------
regress y x if a==3
Source | SS df MS Number of obs = 4
---------+------------------------------ F( 1, 2) = 281.67
Model | 2.1125 1 2.1125 Prob > F = 0.0035
Residual | .015000019 2 .00750001 R-squared = 0.9929
---------+------------------------------ Adj R-squared = 0.9894
Total | 2.12750002 3 .709166673 Root MSE = .0866
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | .65 .0387299 16.783 0.004 .4833589 .8166411
_cons | 2.75 .1423026 19.325 0.003 2.137721 3.362279
------------------------------------------------------------------------------
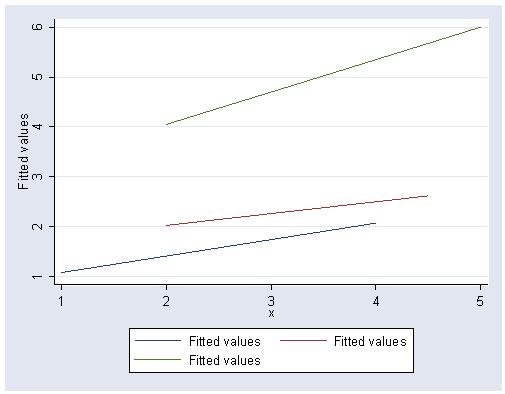
Regression lines for each group Figure 15.2-3, page 716.
graph twoway (lfit y x if a==1) (lfit y x if a==2) (lfit y x if a==3)
Within groups regression coefficient, page 715.
Note: This example uses anova to do regression treating a as categorical and x as continuous.
anova y a c.x
Number of obs = 12 R-squared = 0.9839
Root MSE = .241977 Adj R-squared = 0.9779
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 28.6482438 3 9.5494146 163.09 0.0000
|
a | 20.08945 2 10.044725 171.55 0.0000
x | 2.43657525 1 2.43657525 41.61 0.0002
|
Residual | .468424708 8 .058553088
-----------+----------------------------------------------------
Total | 29.1166685 11 2.64696986
regress
Source | SS df MS Number of obs = 12
-------------+------------------------------ F( 3, 8) = 163.09
Model | 28.6482438 3 9.5494146 Prob > F = 0.0000
Residual | .468424708 8 .058553088 R-squared = 0.9839
-------------+------------------------------ Adj R-squared = 0.9779
Total | 29.1166685 11 2.64696986 Root MSE = .24198
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
a |
2 | .4058219 .1804211 2.25 0.055 -.0102299 .8218737
3 | 3.028082 .1831786 16.53 0.000 2.605672 3.450493
|
x | .4219178 .0654053 6.45 0.000 .2710929 .5727427
_cons | .5202055 .2034081 2.56 0.034 .0511456 .9892653
------------------------------------------------------------------------------
Between groups regression coefficient, page 717.
egen xbar = mean(x)
egen xbarj = mean(x), by(a)
gen diffx= xbarj-xbar
egen ybar = mean(y)
egen ybarj = mean(y), by(a)
gen diffy= ybarj-ybar
regress diffy diffx
Source | SS df MS Number of obs = 12
-------------+------------------------------ F( 1, 10) = 13.19
Model | 14.9063154 1 14.9063154 Prob > F = 0.0046
Residual | 11.3053527 10 1.13053527 R-squared = 0.5687
-------------+------------------------------ Adj R-squared = 0.5256
Total | 26.2116682 11 2.38287892 Root MSE = 1.0633
------------------------------------------------------------------------------
diffy | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
diffx | 2.505263 .6899383 3.63 0.005 .9679848 4.042541
_cons | 0 .3069385 0.00 1.000 -.6839017 .6839017
------------------------------------------------------------------------------
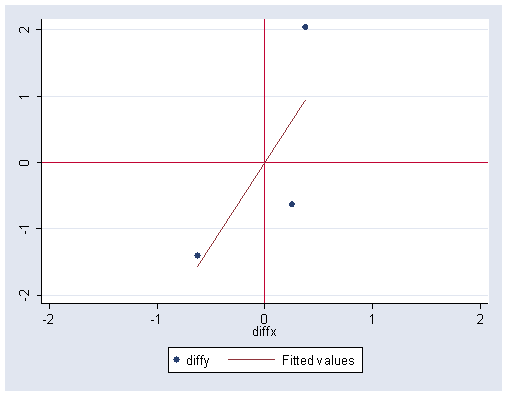
Figure 15.2-4, page 716.
graph twoway (scatter diffy diffx) (lfit diffy diffx), xlabel(-2(1)2) /// ylabel(-2(1)2) xline(0) yline(0)
Total regression coefficient, page 717.
regress y x
Source | SS df MS Number of obs = 12
---------+------------------------------ F( 1, 10) = 4.16
Model | 8.55879381 1 8.55879381 Prob > F = 0.0686
Residual | 20.5578747 10 2.05578747 R-squared = 0.2939
---------+------------------------------ Adj R-squared = 0.2233
Total | 29.1166685 11 2.64696986 Root MSE = 1.4338
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | .7299611 .3577524 2.040 0.069 -.0671609 1.527083
_cons | .7022049 1.192135 0.589 0.569 -1.954038 3.358448
------------------------------------------------------------------------------
Use data file crac4, page 728.
use https://stats.idre.ucla.edu/stat/stata/examples/kirk/crac4, clear
Table 15.3-1, page 720.
sort a
by a: list y x
-> a= 1
y x
1. 3 42
2. 6 57
3. 3 33
4. 3 47
5. 1 32
6. 2 35
7. 2 33
8. 2 39
-> a= 2
y x
9. 4 47
10. 5 49
11. 4 42
12. 3 41
13. 2 38
14. 3 43
15. 4 48
16. 3 45
-> a= 3
y x
17. 7 61
18. 8 65
19. 7 64
20. 6 56
21. 5 52
22. 6 58
23. 5 53
24. 6 54
-> a= 4
y x
25. 7 65
26. 8 74
27. 9 80
28. 8 73
29. 10 85
30. 10 82
31. 9 78
32. 11 89
Table 15.3-2, page 721.
anova y a c.x
Number of obs = 32 R-squared = 0.9701
Root MSE = .510876 Adj R-squared = 0.9656
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 228.453154 4 57.1132885 218.83 0.0000
|
a | 1.79283521 3 .597611737 2.29 0.1010
x | 33.9531542 1 33.9531542 130.09 0.0000
|
Residual | 7.04684582 27 .26099429
-----------+----------------------------------------------------
Total | 235.50 31 7.59677419
Adjusted means, page 725.
adjust x, by(a)
-------------------------------------------------------------------------------
Dependent variable: y Command: anova
Covariate set to mean: x = 55
-------------------------------------------------------------------------------
----------+-----------
a | xb
----------+-----------
1 | 5.31013
2 | 5.32566
3 | 5.76735
4 | 5.09686
----------+-----------
Key: xb = Linear Prediction
Table 15.6-1, page 728.
sort a
by a: list y x z
-> a= 1
y x z
1. 3 42 3
2. 6 57 5
3. 3 33 4
4. 3 47 4
5. 1 32 0
6. 2 35 1
7. 2 33 0
8. 2 39 2
-> a= 2
y x z
9. 4 47 4
10. 5 49 6
11. 4 42 5
12. 3 41 2
13. 2 38 1
14. 3 43 2
15. 4 48 5
16. 3 45 3
-> a= 3
y x z
17. 7 61 5
18. 8 65 7
19. 7 64 5
20. 6 56 4
21. 5 52 2
22. 6 58 3
23. 5 53 3
24. 6 54 4
-> a= 4
y x z
25. 7 65 2
26. 8 74 4
27. 9 80 5
28. 8 73 5
29. 10 85 6
30. 10 82 6
31. 9 78 5
32. 11 89 7
Table 15.6-2, page 729.
Note: The values shown in the book for SSBG, SSWG, MSBG, MSWG, and F are incorrect. The values shown below are correct.
anova y a c.x c.z
Number of obs = 32 R-squared = 0.9836
Root MSE = .385291 Adj R-squared = 0.9805
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 231.640316 5 46.3280631 312.08 0.0000
|
a | 2.65183953 3 .883946509 5.95 0.0031
x | 4.29511432 1 4.29511432 28.93 0.0000
z | 3.18716138 1 3.18716138 21.47 0.0001
|
Residual | 3.85968444 26 .148449402
-----------+----------------------------------------------------
Total | 235.50 31 7.59677419