use https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/catholic, clear
Descriptive statistics for mathematics score (math12) and type of high school (catholic). Note: this output does not appear in the text.
sum math12 catholic, detail
12th grade standardized mathematics score
-------------------------------------------------------------
Percentiles Smallest
1% 32.88 29.88
5% 35.46 30.14
10% 37.54 30.42 Obs 5671
25% 43.53 30.55 Sum of Wgt. 5671
50% 51.33 Mean 51.05124
Largest Std. Dev. 9.502415
75% 58.61 70.94
90% 63.67 71.08 Variance 90.2959
95% 65.98 71.12 Skewness -.0567201
99% 69.33 71.37 Kurtosis 2.072073
attended catholic hs?
-------------------------------------------------------------
Percentiles Smallest
1% 0 0
5% 0 0
10% 0 0 Obs 5671
25% 0 0 Sum of Wgt. 5671
50% 0 Mean .1043908
Largest Std. Dev. .3057938
75% 0 1
90% 1 1 Variance .0935098
95% 1 1 Skewness 2.587653
99% 1 1 Kurtosis 7.69595
table catholic, contents(mean math12 sd math12 freq)
----------------------------------------------------
attended |
catholic |
hs? | mean(math12) sd(math12) Freq.
----------+-----------------------------------------
no | 50.64465 9.534295 5,079
yes | 54.53951 8.463153 592
----------------------------------------------------
Descriptive statistics for family income (faminc8). (Not shown in text.)
sum faminc8, detail
total annual family income in 8th grade
-------------------------------------------------------------
Percentiles Smallest
1% 2 1
5% 5 1
10% 7 1 Obs 5671
25% 8 1 Sum of Wgt. 5671
50% 10 Mean 9.526186
Largest Std. Dev. 2.217688
75% 11 12
90% 12 12 Variance 4.918141
95% 12 12 Skewness -1.268464
99% 12 12 Kurtosis 4.447905
Various methods of examining the relationship between catholic and faminc8. (Not shown in text.)
by catholic, sort: sum faminc8, detail
------------------------------------------------------------------------------------------------------
-> catholic = no
total annual family income in 8th grade
-------------------------------------------------------------
Percentiles Smallest
1% 2 1
5% 5 1
10% 6 1 Obs 5079
25% 8 1 Sum of Wgt. 5079
50% 10 Mean 9.428825
Largest Std. Dev. 2.25239
75% 11 12
90% 12 12 Variance 5.073261
95% 12 12 Skewness -1.214205
99% 12 12 Kurtosis 4.255522
------------------------------------------------------------------------------------------------------
-> catholic = yes
total annual family income in 8th grade
-------------------------------------------------------------
Percentiles Smallest
1% 4 1
5% 7 2
10% 8 4 Obs 592
25% 10 4 Sum of Wgt. 592
50% 11 Mean 10.36149
Largest Std. Dev. 1.67728
75% 11 12
90% 12 12 Variance 2.813269
95% 12 12 Skewness -1.784059
99% 12 12 Kurtosis 7.343344
tab faminc8 catholic, chi2
total annual |
family income | attended catholic hs?
in 8th grade | no yes | Total
----------------+----------------------+----------
none | 17 1 | 18
<$1000 | 41 1 | 42
$1000-$2999 | 84 0 | 84
$3000-$4999 | 79 6 | 85
$5000-$7499 | 138 6 | 144
7500-$9999 | 169 6 | 175
$10000-$14999 | 427 20 | 447
$15000-$19999 | 410 31 | 441
$20000-$24999 | 608 47 | 655
$25000-$34999 | 1,137 130 | 1,267
35000-$49999 | 1,221 198 | 1,419
50000-$74999 | 748 146 | 894
----------------+----------------------+----------
Total | 5,079 592 | 5,671
Pearson chi2(11) = 111.4057 Pr = 0.000
pwcorr faminc8 catholic, sig
| faminc8 catholic
-------------+------------------
faminc8 | 1.0000
|
|
catholic | 0.1286 1.0000
| 0.0000
|
Categorize faminc8 into catfaminc8, and examine the relationship between the two variables. (Not shown in text.)
egen catfaminc8=cut(faminc8), at(1,9,11,13) icodes
tab catfaminc8
catfaminc8 | Freq. Percent Cum.
------------+-----------------------------------
0 | 1,436 25.32 25.32
1 | 1,922 33.89 59.21
2 | 2,313 40.79 100.00
------------+-----------------------------------
Total | 5,671 100.00
tab faminc8 catfaminc8
total annual |
family income | catfaminc8
in 8th grade | 0 1 2 | Total
----------------+---------------------------------+----------
none | 18 0 0 | 18
<$1000 | 42 0 0 | 42
$1000-$2999 | 84 0 0 | 84
$3000-$4999 | 85 0 0 | 85
$5000-$7499 | 144 0 0 | 144
7500-$9999 | 175 0 0 | 175
$10000-$14999 | 447 0 0 | 447
$15000-$19999 | 441 0 0 | 441
$20000-$24999 | 0 655 0 | 655
$25000-$34999 | 0 1,267 0 | 1,267
35000-$49999 | 0 0 1,419 | 1,419
50000-$74999 | 0 0 894 | 894
----------------+---------------------------------+----------
Total | 1,436 1,922 2,313 | 5,671
Table 12.1 on page 293.
* Sample variance of faminc8 in each income category.
tabstat faminc8, by(catfaminc8) statistics(var)
Summary for variables: faminc8
by categories of: catfaminc8
catfaminc8 | variance
-----------+----------
0 | 3.063001
1 | .2247694
2 | .2372228
-----------+----------
Total | 4.918141
----------------------
* Sample mean of faminc8 by income category and school type.
table catfaminc8 catholic, contents(mean faminc8)
------------------------------------------
catfaminc | attended catholic hs?
8 | no yes
----------+-------------------------------
0 | 6.32967042923 6.774647712708
1 | 9.651576042175 9.734463691711
2 | 11.37988853455 11.4244184494
------------------------------------------
* Tests for differences in family income by school type within each income category.
by catfaminc8, sort : ttest faminc8, by(catholic)
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 0
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1365 6.32967 .0475499 1.756773 6.236392 6.422949
yes | 71 6.774648 .1862445 1.569324 6.403195 7.146101
---------+--------------------------------------------------------------------
combined | 1436 6.351671 .0461845 1.750143 6.261075 6.442268
---------+--------------------------------------------------------------------
diff | -.4449776 .2127872 -.8623851 -.0275701
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.0912
Ho: diff = 0 degrees of freedom = 1434
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0183 Pr(|T| > |t|) = 0.0367 Pr(T > t) = 0.9817
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 1
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1745 9.651576 .0114094 .4766077 9.629198 9.673954
yes | 177 9.734463 .0332883 .4428714 9.668768 9.800159
---------+--------------------------------------------------------------------
combined | 1922 9.659209 .0108141 .4740985 9.638 9.680418
---------+--------------------------------------------------------------------
diff | -.0828873 .037361 -.1561597 -.009615
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.2186
Ho: diff = 0 degrees of freedom = 1920
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0133 Pr(|T| > |t|) = 0.0266 Pr(T > t) = 0.9867
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 2
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1969 11.37989 .0109408 .4854821 11.35843 11.40135
yes | 344 11.42442 .0266872 .4949744 11.37193 11.47691
---------+--------------------------------------------------------------------
combined | 2313 11.38651 .0101272 .4870552 11.36665 11.40637
---------+--------------------------------------------------------------------
diff | -.0445303 .028453 -.1003264 .0112657
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -1.5650
Ho: diff = 0 degrees of freedom = 2311
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0589 Pr(|T| > |t|) = 0.1177 Pr(T > t) = 0.9411
tab catfaminc8 catholic, row
+----------------+
| Key |
|----------------|
| frequency |
| row percentage |
+----------------+
| attended catholic hs?
catfaminc8 | no yes | Total
-----------+----------------------+----------
0 | 1,365 71 | 1,436
| 95.06 4.94 | 100.00
-----------+----------------------+----------
1 | 1,745 177 | 1,922
| 90.79 9.21 | 100.00
-----------+----------------------+----------
2 | 1,969 344 | 2,313
| 85.13 14.87 | 100.00
-----------+----------------------+----------
Total | 5,079 592 | 5,671
| 89.56 10.44 | 100.00
* Average math achievement, by school type and income category.
table catfaminc8 catholic, contents(mean math12)
------------------------------
| attended catholic
catfaminc | hs?
8 | no yes
----------+-------------------
0 | 46.77358 50.53563
1 | 50.33842 53.85616
2 | 53.59964 55.7175
------------------------------
* Tests for differences in average math achievement by school type within each income category.
by catfaminc8, sort : ttest math12, by(catholic)
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 0
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1365 46.77358 .2409728 8.90296 46.30086 47.2463
yes | 71 50.53563 1.003933 8.459293 48.53335 52.53792
---------+--------------------------------------------------------------------
combined | 1436 46.95959 .2352876 8.916128 46.49804 47.42113
---------+--------------------------------------------------------------------
diff | -3.762051 1.081144 -5.882845 -1.641258
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -3.4797
Ho: diff = 0 degrees of freedom = 1434
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0003 Pr(|T| > |t|) = 0.0005 Pr(T > t) = 0.9997
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 1
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1745 50.33842 .2228944 9.311012 49.90126 50.77559
yes | 177 53.85616 .6445502 8.575183 52.58412 55.1282
---------+--------------------------------------------------------------------
combined | 1922 50.66238 .2121188 9.299418 50.24637 51.07838
---------+--------------------------------------------------------------------
diff | -3.517734 .7293671 -4.948169 -2.087299
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -4.8230
Ho: diff = 0 degrees of freedom = 1920
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0000 Pr(|T| > |t|) = 0.0000 Pr(T > t) = 1.0000
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 2
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1969 53.59964 .2060271 9.142124 53.19559 54.00369
yes | 344 55.7175 .4384348 8.131754 54.85514 56.57986
---------+--------------------------------------------------------------------
combined | 2313 53.91462 .1877359 9.028905 53.54647 54.28277
---------+--------------------------------------------------------------------
diff | -2.117861 .5258916 -3.149129 -1.086592
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -4.0272
Ho: diff = 0 degrees of freedom = 2311
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0000 Pr(|T| > |t|) = 0.0001 Pr(T > t) = 1.0000
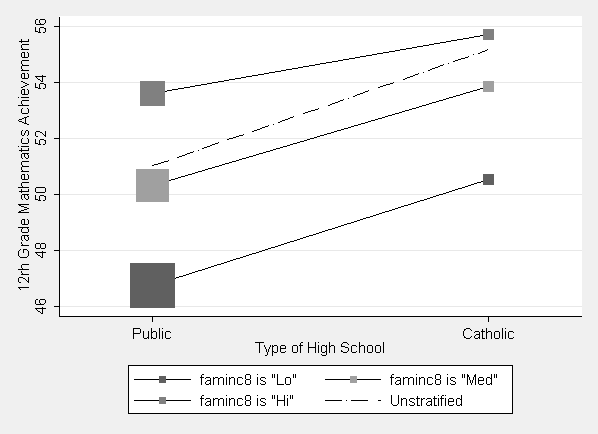
Figure 12.1 on page 297.
sort catholic catfaminc8
by catholic catfaminc8: egen n = count(id)
by catholic catfaminc8: egen mmath12 = mean(math12)
twoway (scatter mmath12 catholic [aweight=n] if catfaminc8==0, connect(l) msymbol(S)) ///
(scatter mmath12 catholic [aweight=n] if catfaminc8==1, connect(l) msymbol(S)) ///
(scatter mmath12 catholic [aweight=n] if catfaminc8==2, connect(l) msymbol(S)) ///
(lfit math12 catholic [aweight=n]), ///
xlabel(0 "Public" 1 "Catholic") xscale(range(-.25 1.25)) ///
legend(label(1 `"faminc8 is "Lo""') label(2 `"faminc8 is "Med""') ///
label(3 `"faminc8 is "Hi""') label(4 `"Unstratified"')) ///
xtitle("Type of High School") ytitle("12rh Grade Mathematics Achievement") ///
scheme(s2mono)
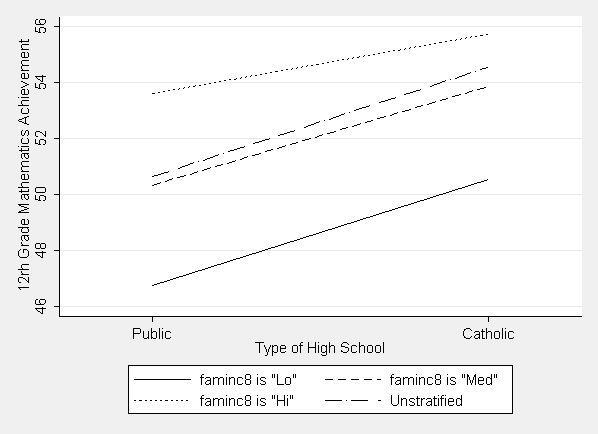
A simplified graph that provides information similar to that in Figure 12.1 can be produced using the syntax shown below. (Not shown in the text.)
twoway (lfit math12 catholic if catfaminc8==0) ///
(lfit math12 catholic if catfaminc8==1) ///
(lfit math12 catholic if catfaminc8==2) ///
(lfit math12 catholic), ///
xlabel(0 "Public" 1 "Catholic") xscale(range(-.25 1.25)) ///
legend(label(1 `"faminc8 is "Lo""') label(2 `"faminc8 is "Med""') ///
label(3 `"faminc8 is "Hi""') label(4 `"Unstratified"')) ///
xtitle("Type of High School") ytitle("12rh Grade Mathematics Achievement") ///
scheme(s2mono)
OLS regression model of math12 on catholic. This regression corresponds to the "Unstratified" line in Figure 12.1. (Not shown in the text.)
regress math12 catholic
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 1, 5669) = 90.48
Model | 8043.1077 1 8043.1077 Prob > F = 0.0000
Residual | 503934.635 5669 88.8930385 R-squared = 0.0157
-------------+------------------------------ Adj R-squared = 0.0155
Total | 511977.743 5670 90.2958982 Root MSE = 9.4283
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 3.89486 .4094621 9.51 0.000 3.092157 4.697562
_cons | 50.64465 .1322954 382.81 0.000 50.3853 50.904
------------------------------------------------------------------------------
OLS regression of math12 on catholic, stratifying by catfaminc8. These regressions correspond to the information shown in Figure 12.1. (Not shown in text.)
by catfaminc8, sort: regress math12 catholic
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 0
Source | SS df MS Number of obs = 1436
-------------+------------------------------ F( 1, 1434) = 12.11
Model | 955.181769 1 955.181769 Prob > F = 0.0005
Residual | 113123.499 1434 78.8866802 R-squared = 0.0084
-------------+------------------------------ Adj R-squared = 0.0077
Total | 114078.681 1435 79.4973388 Root MSE = 8.8818
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 3.762051 1.081144 3.48 0.001 1.641258 5.882845
_cons | 46.77358 .2404006 194.57 0.000 46.30201 47.24516
------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 1
Source | SS df MS Number of obs = 1922
-------------+------------------------------ F( 1, 1920) = 23.26
Model | 1988.57183 1 1988.57183 Prob > F = 0.0000
Residual | 164137.924 1920 85.4885019 R-squared = 0.0120
-------------+------------------------------ Adj R-squared = 0.0115
Total | 166126.496 1921 86.4791752 Root MSE = 9.246
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 3.517734 .7293671 4.82 0.000 2.087299 4.948169
_cons | 50.33842 .2213381 227.43 0.000 49.90434 50.77251
------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 2
Source | SS df MS Number of obs = 2313
-------------+------------------------------ F( 1, 2311) = 16.22
Model | 1313.47946 1 1313.47946 Prob > F = 0.0001
Residual | 187163.381 2311 80.9880488 R-squared = 0.0070
-------------+------------------------------ Adj R-squared = 0.0065
Total | 188476.86 2312 81.5211333 Root MSE = 8.9993
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 2.117861 .5258916 4.03 0.000 1.086592 3.149129
_cons | 53.59964 .2028092 264.29 0.000 53.20193 53.99735
------------------------------------------------------------------------------
Descriptive statistics for math achievement (math8). (Not shown in text.)
sum math8, detail
8th grade standardized mathematics score
-------------------------------------------------------------
Percentiles Smallest
1% 35.95 34.48
5% 37.89 34.49
10% 39.42 34.52 Obs 5671
25% 43.45 34.52 Sum of Wgt. 5671
50% 50.45 Mean 51.48952
Largest Std. Dev. 9.683425
75% 58.56 77.2
90% 65.39 77.2 Variance 93.76872
95% 68.89 77.2 Skewness .4078902
99% 74.04 77.2 Kurtosis 2.319295
Several methods of examining the relationship between math8 and catholic. (Not shown in text.)
corr math8 catholic
(obs=5671)
| math8 catholic
-------------+------------------
math8 | 1.0000
catholic | 0.0765 1.0000
ttest math8, by(catholic)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 5079 51.23648 .1367773 9.747724 50.96834 51.50462
yes | 592 53.66039 .3628002 8.82731 52.94785 54.37292
---------+--------------------------------------------------------------------
combined | 5671 51.48952 .1285876 9.683425 51.23743 51.7416
---------+--------------------------------------------------------------------
diff | -2.423907 .4193447 -3.245983 -1.601831
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -5.7802
Ho: diff = 0 degrees of freedom = 5669
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0000 Pr(|T| > |t|) = 0.0000 Pr(T > t) = 1.0000
Create a categorical variable for prior math achievement (catmath8), and examine the relationship between cathmath8 and math8. (Not shown in text.)
egen catmath8=cut(math8), at(30,38,44,51,80) icodes
tab catmath8
catmath8 | Freq. Percent Cum.
------------+-----------------------------------
0 | 304 5.36 5.36
1 | 1,236 21.80 27.16
2 | 1,421 25.06 52.21
3 | 2,710 47.79 100.00
------------+-----------------------------------
Total | 5,671 100.00
table catmath8, contents(mean math8 sd math8 freq)
-------------------------------------------------
catmath8 | mean(math8) sd(math8) Freq.
----------+--------------------------------------
0 | 36.78859 .8564365 304
1 | 41.10199 1.722423 1,236
2 | 47.53923 2.045117 1,421
3 | 59.9476 6.27689 2,710
-------------------------------------------------
Check for balance in math8 within strata (catmath8), by catholic. (Not shown in the text.)
table catmath8 catholic, contents(mean math8 sd math8 freq)
------------------------------
| attended catholic
| hs?
catmath8 | no yes
----------+-------------------
0 | 36.80332 36.30556
| .8559109 .7666504
| 295 9
|
1 | 41.09058 41.2438
| 1.718102 1.778788
| 1,144 92
|
2 | 47.49826 47.92955
| 2.040288 2.057497
| 1,286 135
|
3 | 60.01815 59.48112
| 6.348762 5.765806
| 2,354 356
------------------------------
by catmath8, sort : ttest math8, by(catholic)
------------------------------------------------------------------------------------------------------
-> catmath8 = 0
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 295 36.80332 .0498331 .8559109 36.70525 36.9014
yes | 9 36.30556 .2555501 .7666504 35.71626 36.89486
---------+--------------------------------------------------------------------
combined | 304 36.78859 .04912 .8564365 36.69193 36.88525
---------+--------------------------------------------------------------------
diff | .4977666 .2888636 -.0706738 1.066207
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = 1.7232
Ho: diff = 0 degrees of freedom = 302
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.9571 Pr(|T| > |t|) = 0.0859 Pr(T > t) = 0.0429
------------------------------------------------------------------------------------------------------
-> catmath8 = 1
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1144 41.09059 .0507967 1.718102 40.99092 41.19025
yes | 92 41.2438 .1854515 1.778788 40.87543 41.61218
---------+--------------------------------------------------------------------
combined | 1236 41.10199 .0489926 1.722423 41.00587 41.19811
---------+--------------------------------------------------------------------
diff | -.1532187 .1866807 -.5194654 .213028
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -0.8208
Ho: diff = 0 degrees of freedom = 1234
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.2060 Pr(|T| > |t|) = 0.4119 Pr(T > t) = 0.7940
------------------------------------------------------------------------------------------------------
-> catmath8 = 2
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1286 47.49826 .0568946 2.040288 47.38664 47.60987
yes | 135 47.92956 .1770811 2.057497 47.57932 48.27979
---------+--------------------------------------------------------------------
combined | 1421 47.53923 .0542527 2.045117 47.43281 47.64566
---------+--------------------------------------------------------------------
diff | -.4312974 .1847346 -.7936796 -.0689152
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.3347
Ho: diff = 0 degrees of freedom = 1419
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0098 Pr(|T| > |t|) = 0.0197 Pr(T > t) = 0.9902
------------------------------------------------------------------------------------------------------
-> catmath8 = 3
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 2354 60.01815 .1308536 6.348762 59.76155 60.27475
yes | 356 59.48112 .3055871 5.765806 58.88013 60.08211
---------+--------------------------------------------------------------------
combined | 2710 59.9476 .1205757 6.27689 59.71117 60.18403
---------+--------------------------------------------------------------------
diff | .5370243 .3568614 -.1627239 1.236773
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = 1.5049
Ho: diff = 0 degrees of freedom = 2708
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.9338 Pr(|T| > |t|) = 0.1325 Pr(T > t) = 0.0662
Table 12.1 on page 301.
table catmath8 catholic , contents(mean math12 freq) by(catfaminc8)
------------------------------
catfaminc | attended catholic
8 and | hs?
catmath8 | no yes
----------+-------------------
0 |
0 | 36.80514 42.57
| 142 1
|
1 | 40.99247 41.7019
| 433 21
|
2 | 47.12156 48.65308
| 385 13
|
3 | 56.11869 56.58972
| 405 36
----------+-------------------
1 |
0 | 37.94156 39.775
| 96 2
|
1 | 41.92456 44.56454
| 390 33
|
2 | 47.9487 50.13551
| 469 49
|
3 | 57.41727 59.41634
| 790 93
----------+-------------------
2 |
0 | 39.78667 40.40334
| 57 6
|
1 | 42.7458 44.22737
| 321 38
|
2 | 49.17894 50.70644
| 432 73
|
3 | 58.93283 59.65723
| 1,159 227
------------------------------
The t-tests shown in Table 12.1 on page 301 can be reproduced using the following syntax. (Note: most of the output was omitted to save space.)
bysort catfaminc8 catmath8: ttest math12, by(catholic)
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 0, catmath8 = 0
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 142 36.80514 .3391017 4.040863 36.13476 37.47552
yes | 1 42.57 . . . .
---------+--------------------------------------------------------------------
combined | 143 36.84545 . . . .
---------+--------------------------------------------------------------------
diff | -5.764859 . . .
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = .
Ho: diff = 0 degrees of freedom = 141
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = . Pr(|T| > |t|) = . Pr(T > t) = .
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 0, catmath8 = 1
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 433 40.99247 .2466134 5.131692 40.50776 41.47718
yes | 21 41.7019 1.018852 4.668968 39.57662 43.82719
---------+--------------------------------------------------------------------
combined | 454 41.02529 .2397602 5.108636 40.55411 41.49647
---------+--------------------------------------------------------------------
diff | -.7094334 1.142284 -2.954279 1.535412
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -0.6211
Ho: diff = 0 degrees of freedom = 452
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.2674 Pr(|T| > |t|) = 0.5349 Pr(T > t) = 0.7326
------------------------------------------------------------------------------------------------------
-> catfaminc8 = 0, catmath8 = 2
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 385 47.12156 .2927101 5.743387 46.54604 47.69707
yes | 13 48.65308 1.413799 5.097526 45.57267 51.73348
---------+--------------------------------------------------------------------
combined | 398 47.17158 .2869264 5.724165 46.6075 47.73567
---------+--------------------------------------------------------------------
diff | -1.531519 1.614382 -4.70535 1.642312
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -0.9487
Ho: diff = 0 degrees of freedom = 396
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.1717 Pr(|T| > |t|) = 0.3434 Pr(T > t) = 0.8283
Estimate the relationship between math12 and catholic separately in each of the strata (catfaminc8 and catmath8) and save the results to a new dataset (cathslopes2.dta). (Note: this output does not appear in the text and most of the output was omitted to save space.)
sort catfaminc8 catmath8
statsby diff=_b[catholic] n=e(N), by(catfaminc8 catmath8) noisily sav(cathslopes2, replace): ///
regress math12 catholic
statsby: First call to regress with data as is:
. regress math12 catholic
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 1, 5669) = 90.48
Model | 8043.1077 1 8043.1077 Prob > F = 0.0000
Residual | 503934.635 5669 88.8930385 R-squared = 0.0157
-------------+------------------------------ Adj R-squared = 0.0155
Total | 511977.743 5670 90.2958982 Root MSE = 9.4283
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 3.89486 .4094621 9.51 0.000 3.092157 4.697562
_cons | 50.64465 .1322954 382.81 0.000 50.3853 50.904
------------------------------------------------------------------------------
statsby legend:
command: regress math12 catholic
diff: _b[catholic]
n: e(N)
by: catfaminc8 catmath8
Statsby groups
running (regress math12 catholic) on group 1
. regress math12 catholic
Source | SS df MS Number of obs = 143
-------------+------------------------------ F( 1, 141) = 2.02
Model | 33.0011957 1 33.0011957 Prob > F = 0.1573
Residual | 2302.32862 141 16.3285718 R-squared = 0.0141
-------------+------------------------------ Adj R-squared = 0.0071
Total | 2335.32981 142 16.4459846 Root MSE = 4.0409
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 5.764859 4.055066 1.42 0.157 -2.251729 13.78145
_cons | 36.80514 .3391017 108.54 0.000 36.13476 37.47552
------------------------------------------------------------------------------
running (regress math12 catholic) on group 2
. regress math12 catholic
Source | SS df MS Number of obs = 454
-------------+------------------------------ F( 1, 452) = 0.39
Model | 10.0803278 1 10.0803278 Prob > F = 0.5349
Residual | 11812.3885 452 26.1336029 R-squared = 0.0009
-------------+------------------------------ Adj R-squared = -0.0014
Total | 11822.4689 453 26.0981652 Root MSE = 5.1121
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | .7094334 1.142284 0.62 0.535 -1.535412 2.954279
_cons | 40.99247 .245672 166.86 0.000 40.50967 41.47527
------------------------------------------------------------------------------
Graph the resulting slopes. Note that the entire block of syntax should be run and once. (Not shown in the text.)
preserve
use https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/cathslopes2, clear
list
histogram diff, bin(6) frequency kdensity kdenopts(gaussian)
restore
+---------------------------------------+
| catfam~8 catmath8 diff n |
|---------------------------------------|
1. | 0 0 5.764859 143 |
2. | 0 1 .7094334 454 |
3. | 0 2 1.531519 398 |
4. | 0 3 .471031 441 |
5. | 1 0 1.833437 98 |
|---------------------------------------|
6. | 1 1 2.639981 423 |
7. | 1 2 2.186811 518 |
8. | 1 3 1.999078 883 |
9. | 2 0 .6166673 63 |
10. | 2 1 1.481574 359 |
|---------------------------------------|
11. | 2 2 1.527503 505 |
12. | 2 3 .7243947 1386 |
+---------------------------------------+
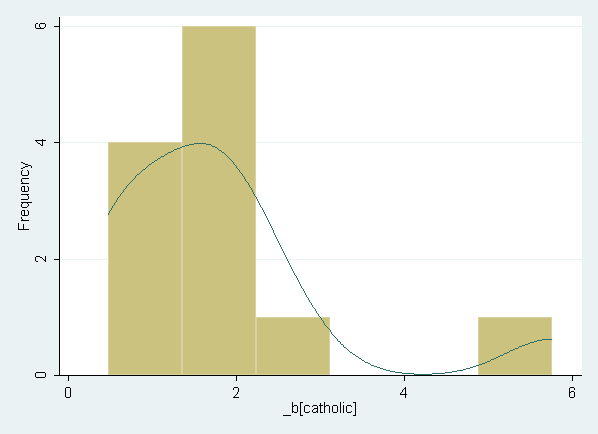
Similar to model A from Table 12.3 on page 306, but with dummy variables representing the catfaminc8 by catmath8 interaction (with one group omitted as the reference category). (Not shown in text.)
xi: regress math12 catholic i.catfaminc8*i.catmath8
i.catfaminc8 _Icatfaminc_0-2 (naturally coded; _Icatfaminc_0 omitted)
i.catmath8 _Icatmath8_0-3 (naturally coded; _Icatmath8_0 omitted)
i.ca~c8*i.ca~h8 _IcatXcat_#_# (coded as above)
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 12, 5658) = 710.06
Model | 307674.539 12 25639.5449 Prob > F = 0.0000
Residual | 204303.204 5658 36.1087317 R-squared = 0.6010
-------------+------------------------------ Adj R-squared = 0.6001
Total | 511977.743 5670 90.2958982 Root MSE = 6.0091
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.328632 .2639492 5.03 0.000 .8111899 1.846073
_Icatfamin~1 | 1.115701 .7880213 1.42 0.157 -.4291226 2.660525
_Icatfamin~2 | 2.882697 .9089585 3.17 0.002 1.10079 4.664604
_Icatmath8_1 | 4.127667 .5763251 7.16 0.000 2.997848 5.257485
_Icatmath8_2 | 10.29202 .585901 17.57 0.000 9.143432 11.44061
_Icatmath8_3 | 19.21252 .5785983 33.21 0.000 18.07825 20.34679
_IcatXca~1_1 | -.0526632 .8865024 -0.06 0.953 -1.790548 1.685221
_IcatXca~1_2 | -.2140083 .8840602 -0.24 0.809 -1.947105 1.519089
_IcatXca~1_3 | .3234948 .8624064 0.38 0.708 -1.367152 2.014142
_IcatXca~2_1 | -1.084544 1.002914 -1.08 0.280 -3.050639 .8815522
_IcatXca~2_2 | -.8031993 .9939466 -0.81 0.419 -2.751716 1.145317
_IcatXca~2_3 | -.0975123 .9662284 -0.10 0.920 -1.99169 1.796666
_cons | 36.83616 .5025057 73.30 0.000 35.85106 37.82127
------------------------------------------------------------------------------
The above model can also be specified using the factor variable syntax introduced in Stata 11.
regress math12 catholic catfaminc8##catmath8
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 12, 5658) = 710.06
Model | 307674.539 12 25639.5449 Prob > F = 0.0000
Residual | 204303.204 5658 36.1087317 R-squared = 0.6010
-------------+------------------------------ Adj R-squared = 0.6001
Total | 511977.743 5670 90.2958982 Root MSE = 6.0091
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.328632 .2639492 5.03 0.000 .8111899 1.846073
|
catfaminc8 |
1 | 1.115701 .7880213 1.42 0.157 -.4291226 2.660525
2 | 2.882697 .9089585 3.17 0.002 1.10079 4.664604
|
catmath8 |
1 | 4.127667 .5763251 7.16 0.000 2.997848 5.257485
2 | 10.29202 .585901 17.57 0.000 9.143432 11.44061
3 | 19.21252 .5785983 33.21 0.000 18.07825 20.34679
|
catfaminc8#|
catmath8 |
1 1 | -.0526632 .8865024 -0.06 0.953 -1.790548 1.685221
1 2 | -.2140083 .8840602 -0.24 0.809 -1.947105 1.519089
1 3 | .3234948 .8624064 0.38 0.708 -1.367152 2.014142
2 1 | -1.084544 1.002914 -1.08 0.280 -3.050639 .8815522
2 2 | -.8031993 .9939466 -0.81 0.419 -2.751716 1.145317
2 3 | -.0975123 .9662284 -0.10 0.920 -1.99169 1.796666
|
_cons | 36.83616 .5025057 73.30 0.000 35.85106 37.82127
------------------------------------------------------------------------------
Table 12.3 on page 306, the Stratified, Fully Crossed model. Note the noomit option of the xi command is used so that a full set of dummy variables is created (i.e. one for each category). Then the constant is suppressed (i.e. noconstant) so that all dummy variables can be included.
xi i.catfaminc8*i.catmath8, noomit
i.ca~c8*i.ca~h8 _IcatXcat_#_# (coded as above)
regress math12 catholic _IcatXcat_0_0-_IcatXcat_2_3, noconstant
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 13, 5658) =32141.38
Model | 15087598.6 13 1160584.51 Prob > F = 0.0000
Residual | 204303.204 5658 36.1087317 R-squared = 0.9866
-------------+------------------------------ Adj R-squared = 0.9866
Total | 15291901.8 5671 2696.50887 Root MSE = 6.0091
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.328632 .2639492 5.03 0.000 .8111899 1.846073
_IcatXca~0_0 | 36.83616 .5025057 73.30 0.000 35.85106 37.82127
_IcatXca~0_1 | 40.96383 .282283 145.12 0.000 40.41045 41.51721
_IcatXca~0_2 | 47.12819 .30133 156.40 0.000 46.53746 47.71891
_IcatXca~0_3 | 56.04868 .2869555 195.32 0.000 55.48614 56.61123
_IcatXca~1_0 | 37.95186 .60703 62.52 0.000 36.76185 39.14188
_IcatXca~1_1 | 42.02687 .292895 143.49 0.000 41.45268 42.60105
_IcatXca~1_2 | 48.02988 .2652007 181.11 0.000 47.50998 48.54977
_IcatXca~1_3 | 57.48788 .2041227 281.63 0.000 57.08772 57.88804
_IcatXca~2_0 | 39.71886 .7574869 52.44 0.000 38.2339 41.20382
_IcatXca~2_1 | 42.76198 .318374 134.31 0.000 42.13785 43.38612
_IcatXca~2_2 | 49.20768 .2701078 182.18 0.000 48.67817 49.7372
_IcatXca~2_3 | 58.83387 .1670966 352.09 0.000 58.50629 59.16144
------------------------------------------------------------------------------
The above model (model A from Table 12.3) can also be estimated using the factor variable syntax introduced in Stata 11. Note again that all of the groups are included and the intercept (constant) is omitted.
regress math12 catholic ibn.catfaminc8#ibn.catmath8, noconstant
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 13, 5658) =32141.38
Model | 15087598.6 13 1160584.51 Prob > F = 0.0000
Residual | 204303.204 5658 36.1087317 R-squared = 0.9866
-------------+------------------------------ Adj R-squared = 0.9866
Total | 15291901.8 5671 2696.50887 Root MSE = 6.0091
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.328632 .2639492 5.03 0.000 .8111899 1.846073
|
catfaminc8#|
catmath8 |
0 0 | 36.83616 .5025057 73.30 0.000 35.85106 37.82127
0 1 | 40.96383 .282283 145.12 0.000 40.41045 41.51721
0 2 | 47.12819 .30133 156.40 0.000 46.53746 47.71891
0 3 | 56.04868 .2869555 195.32 0.000 55.48614 56.61123
1 0 | 37.95186 .60703 62.52 0.000 36.76185 39.14188
1 1 | 42.02687 .292895 143.49 0.000 41.45268 42.60105
1 2 | 48.02988 .2652007 181.11 0.000 47.50998 48.54977
1 3 | 57.48788 .2041227 281.63 0.000 57.08772 57.88804
2 0 | 39.71886 .7574869 52.44 0.000 38.2339 41.20382
2 1 | 42.76198 .318374 134.31 0.000 42.13785 43.38612
2 2 | 49.20768 .2701078 182.18 0.000 48.67817 49.7372
2 3 | 58.83387 .1670966 352.09 0.000 58.50629 59.16144
------------------------------------------------------------------------------
Table 12.3 on page 306, the Linear Main Effects, Two-way Interaction model.
logit catholic inc8 math8 mathfam
Iteration 0: log likelihood = -1897.6568
Iteration 1: log likelihood = -1840.7214
Iteration 2: log likelihood = -1837.6029
Iteration 3: log likelihood = -1837.5922
Iteration 4: log likelihood = -1837.5922
Logistic regression Number of obs = 5671
LR chi2(3) = 120.13
Prob > chi2 = 0.0000
Log likelihood = -1837.5922 Pseudo R2 = 0.0317
------------------------------------------------------------------------------
catholic | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .0618026 .0140542 4.40 0.000 .0342569 .0893482
math8 | .0429594 .011135 3.86 0.000 .0211352 .0647836
mathfam | -.000734 .0002615 -2.81 0.005 -.0012466 -.0002214
_cons | -5.208846 .5863848 -8.88 0.000 -6.358139 -4.059553
------------------------------------------------------------------------------
* Recode faminc8 so that the values are actual mid-values of income in $1000:
recode faminc8 (1=0) (2=.5) (3=2) (4=4) (5=6.25) (6=8.75) ///
(7=12.5) (8=17.5) (9=22.5) (10=30) (11=42.5) (12=62.5), gen(inc8)
(5586 differences between faminc8 and inc8)
gen mathfam = math8*inc8
regress math12 inc8 math8 mathfam catholic
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 4, 5666) = 3259.30
Model | 356877.886 4 89219.4715 Prob > F = 0.0000
Residual | 155099.857 5666 27.3737834 R-squared = 0.6971
-------------+------------------------------ Adj R-squared = 0.6968
Total | 511977.743 5670 90.2958982 Root MSE = 5.232
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .1638722 .0218124 7.51 0.000 .1211115 .2066329
math8 | .8721913 .0160066 54.49 0.000 .8408123 .9035703
mathfam | -.002435 .0004171 -5.84 0.000 -.0032527 -.0016173
catholic | 1.658869 .2295556 7.23 0.000 1.208852 2.108886
_cons | 4.827092 .8004556 6.03 0.000 3.257892 6.396291
------------------------------------------------------------------------------
The above model (model B from Table 12.3) can also be estimated using the factor variable syntax introduced in Stata 11. Note that it is still necessary to recode faminc8 into inc8, but it is not necessary to create the interaction term.
regress math12 c.inc8##c.math8 catholic
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 4, 5666) = 3259.30
Model | 356877.886 4 89219.4715 Prob > F = 0.0000
Residual | 155099.857 5666 27.3737834 R-squared = 0.6971
-------------+------------------------------ Adj R-squared = 0.6968
Total | 511977.743 5670 90.2958982 Root MSE = 5.232
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .1638722 .0218124 7.51 0.000 .1211115 .2066329
math8 | .8721913 .0160066 54.49 0.000 .8408123 .9035703
|
c.inc8#|
c.math8 | -.002435 .0004171 -5.84 0.000 -.0032527 -.0016173
|
catholic | 1.658869 .2295556 7.23 0.000 1.208852 2.108886
_cons | 4.827092 .8004556 6.03 0.000 3.257892 6.396291
------------------------------------------------------------------------------
Table 12.4, Model A: Initial specification, with linear main effect of inc8, on page 312.
logit catholic inc8 math8 mathfam
Iteration 0: log likelihood = -1897.6568
Iteration 1: log likelihood = -1840.7214
Iteration 2: log likelihood = -1837.6029
Iteration 3: log likelihood = -1837.5922
Iteration 4: log likelihood = -1837.5922
Logistic regression Number of obs = 5671
LR chi2(3) = 120.13
Prob > chi2 = 0.0000
Log likelihood = -1837.5922 Pseudo R2 = 0.0317
------------------------------------------------------------------------------
catholic | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .0618026 .0140542 4.40 0.000 .0342569 .0893482
math8 | .0429594 .011135 3.86 0.000 .0211352 .0647836
mathfam | -.000734 .0002615 -2.81 0.005 -.0012466 -.0002214
_cons | -5.208846 .5863848 -8.88 0.000 -6.358139 -4.059553
------------------------------------------------------------------------------
Table 12.4, Model B: Final specification, with quadratic main effect of inc8, on page 312.
gen inc8sq = inc8*inc8
logit catholic inc8 math8 mathfam inc8sq
Iteration 0: log likelihood = -1897.6568
Iteration 1: log likelihood = -1838.7904
Iteration 2: log likelihood = -1833.5513
Iteration 3: log likelihood = -1833.5413
Iteration 4: log likelihood = -1833.5413
Logistic regression Number of obs = 5671
LR chi2(4) = 128.23
Prob > chi2 = 0.0000
Log likelihood = -1833.5413 Pseudo R2 = 0.0338
------------------------------------------------------------------------------
catholic | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .0869049 .017354 5.01 0.000 .0528918 .120918
math8 | .0355965 .0119779 2.97 0.003 .0121202 .0590728
mathfam | -.0005647 .0002821 -2.00 0.045 -.0011175 -.0000119
inc8sq | -.0004382 .0001569 -2.79 0.005 -.0007458 -.0001306
_cons | -5.362148 .6190447 -8.66 0.000 -6.575453 -4.148842
------------------------------------------------------------------------------
predict p
(option pr assumed; Pr(catholic))
Model B from Table 12.4 on page 312 can also be estimated using the factor variable syntax introduced in Stata 11. Note that it is not necessary to create the squared term before running this model.
logit catholic inc8 math8 mathfam c.inc8#c.inc8
Iteration 0: log likelihood = -1897.6568
Iteration 1: log likelihood = -1838.7904
Iteration 2: log likelihood = -1833.5513
Iteration 3: log likelihood = -1833.5413
Iteration 4: log likelihood = -1833.5413
Logistic regression Number of obs = 5671
LR chi2(4) = 128.23
Prob > chi2 = 0.0000
Log likelihood = -1833.5413 Pseudo R2 = 0.0338
------------------------------------------------------------------------------
catholic | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .0869049 .017354 5.01 0.000 .0528918 .120918
math8 | .0355965 .0119779 2.97 0.003 .0121202 .0590728
mathfam | -.0005647 .0002821 -2.00 0.045 -.0011175 -.0000119
|
c.inc8#|
c.inc8 | -.0004382 .0001569 -2.79 0.005 -.0007458 -.0001306
|
_cons | -5.362148 .6190447 -8.66 0.000 -6.575453 -4.148842
------------------------------------------------------------------------------
predict p
(option pr assumed; Pr(catholic))
Detailed summary statistics for the propensity score variable p. (Not shown in text.)
sum p, detail
Pr(catholic)
-------------------------------------------------------------
Percentiles Smallest
1% .0208345 .0164257
5% .0320812 .016906
10% .0408222 .0170297 Obs 5671
25% .0672965 .017208 Sum of Wgt. 5671
50% .1056115 Mean .1043908
Largest Std. Dev. .0440799
75% .142168 .1729462
90% .1643515 .1729462 Variance .001943
95% .1647264 .1729462 Skewness -.1636008
99% .1652305 .1729462 Kurtosis 1.83253
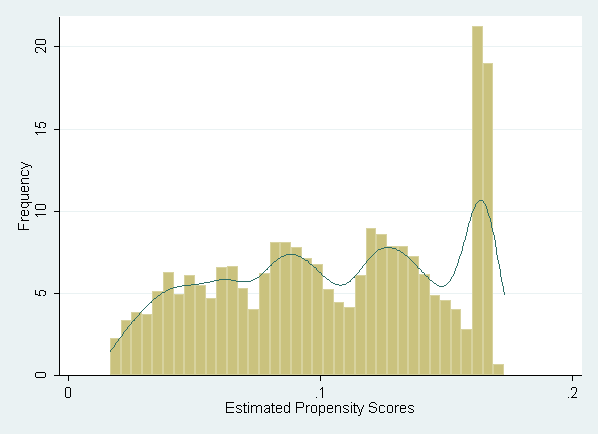
Figure 12.2, Panel A: Full Sample, shown on page 315.
histogram p, kdensity kdenopts(gaussian) xlabel(0(.1).2) /// ytitle(Frequency) xtitle(Estimated Propensity Scores)
Summary statistics for the propesnity score variable p, by catholic.
by catholic, sort: sum p, detail
-------------------------------------------------------------------------------------------
-> catholic = no
Pr(catholic)
-------------------------------------------------------------
Percentiles Smallest
1% .0204874 .0164257
5% .0304734 .016906
10% .0398502 .0170297 Obs 5079
25% .0643826 .017208 Sum of Wgt. 5079
50% .1018312 Mean .1022535
Largest Std. Dev. .0442736
75% .1395716 .1729462
90% .1642913 .1729462 Variance .0019602
95% .1647052 .1729462 Skewness -.1037761
99% .1652047 .1729462 Kurtosis 1.814756
-------------------------------------------------------------------------------------------
-> catholic = yes
Pr(catholic)
-------------------------------------------------------------
Percentiles Smallest
1% .0311486 .0221945
5% .0498571 .0255137
10% .066539 .0260665 Obs 592
25% .0935338 .0266655 Sum of Wgt. 592
50% .1307598 Mean .122727
Largest Std. Dev. .0377261
75% .1636715 .1654167
90% .1645418 .1659938 Variance .0014233
95% .1648288 .1668626 Skewness -.6233737
99% .1652885 .1729462 Kurtosis 2.378922
Figure 12.2, Panel B: By catholic, shown on page 315.
histogram p, kdensity kdenopts(gaussian) by(catholic, cols(1) legend(off)) /// xlabel(0(.1).2) ytitle(Frequency) xtitle(Estimated Propensity Scores)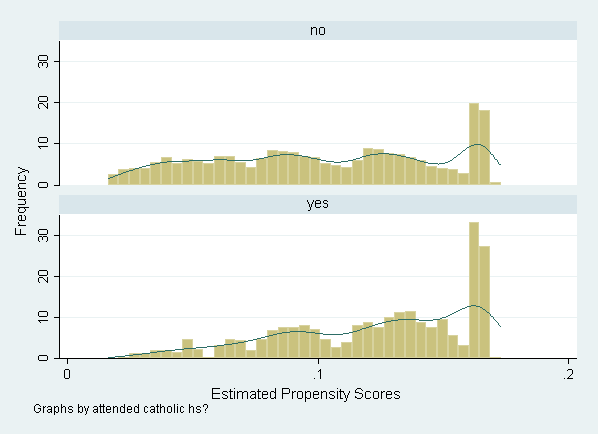
Stratifying on propensity scores, discussed on pages 316-317. This uses the same set of variables as Model A from Table 12.4. Note that pscore is a user-written command, and must be downloaded prior to use, for more information see our FAQ page How do I use search to search for programs and additional help?. (Not shown in text.)
pscore catholic inc8 math8 mathfam, logit pscore(p) blockid(b) numblo(5)
****************************************************
Algorithm to estimate the propensity score
****************************************************
The treatment is catholic
attended |
catholic |
hs? | Freq. Percent Cum.
------------+-----------------------------------
no | 5,079 89.56 89.56
yes | 592 10.44 100.00
------------+-----------------------------------
Total | 5,671 100.00
Estimation of the propensity score
Iteration 0: log likelihood = -1897.6568
Iteration 1: log likelihood = -1840.7214
Iteration 2: log likelihood = -1837.6047
Iteration 3: log likelihood = -1837.5922
Iteration 4: log likelihood = -1837.5922
Logistic regression Number of obs = 5671
LR chi2(3) = 120.13
Prob > chi2 = 0.0000
Log likelihood = -1837.5922 Pseudo R2 = 0.0317
------------------------------------------------------------------------------
catholic | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .0618026 .0140542 4.40 0.000 .0342569 .0893482
math8 | .0429594 .011135 3.86 0.000 .0211352 .0647836
mathfam | -.000734 .0002615 -2.81 0.005 -.0012466 -.0002214
_cons | -5.208846 .5863848 -8.88 0.000 -6.358139 -4.059553
------------------------------------------------------------------------------
Description of the estimated propensity score
Estimated propensity score
-------------------------------------------------------------
Percentiles Smallest
1% .0300386 .0241574
5% .0400463 .0250049
10% .0488683 .0252239 Obs 5671
25% .0700201 .02554 Sum of Wgt. 5671
50% .1023014 Mean .1043908
Largest Std. Dev. .0442227
75% .1299765 .1898257
90% .1795338 .1898437 Variance .0019556
95% .1835134 .1899649 Skewness .3693322
99% .187957 .1900232 Kurtosis 2.215181
******************************************************
Step 1: Identification of the optimal number of blocks
Use option detail if you want more detailed output
******************************************************
The final number of blocks is 4
This number of blocks ensures that the mean propensity score
is not different for treated and controls in each blocks
**********************************************************
Step 2: Test of balancing property of the propensity score
Use option detail if you want more detailed output
**********************************************************
Variable inc8 is not balanced in block 4
Variable mathfam is not balanced in block 4
The balancing property is not satisfied
Try a different specification of the propensity score
Inferior |
of block | attended catholic hs?
of pscore | no yes | Total
-----------+----------------------+----------
0 | 588 18 | 606
.05 | 1,002 56 | 1,058
.075 | 1,010 113 | 1,123
.1 | 2,479 405 | 2,884
-----------+----------------------+----------
Total | 5,079 592 | 5,671
*******************************************
End of the algorithm to estimate the pscore
*******************************************
Estimate the propensity score blocks shown in Table 12.5 on page 318. (Output not shown in text.)
* drop propensity score variables if they already exist
drop p b
pscore catholic inc8 inc8sq math8 mathfam, logit pscore(p) blockid(b) numblo(5)
****************************************************
Algorithm to estimate the propensity score
****************************************************
The treatment is catholic
attended |
catholic |
hs? | Freq. Percent Cum.
------------+-----------------------------------
no | 5,079 89.56 89.56
yes | 592 10.44 100.00
------------+-----------------------------------
Total | 5,671 100.00
Estimation of the propensity score
Iteration 0: log likelihood = -1897.6568
Iteration 1: log likelihood = -1838.7904
Iteration 2: log likelihood = -1833.6223
Iteration 3: log likelihood = -1833.5413
Iteration 4: log likelihood = -1833.5413
Logistic regression Number of obs = 5671
LR chi2(4) = 128.23
Prob > chi2 = 0.0000
Log likelihood = -1833.5413 Pseudo R2 = 0.0338
------------------------------------------------------------------------------
catholic | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .0869049 .017354 5.01 0.000 .0528918 .120918
inc8sq | -.0004382 .0001569 -2.79 0.005 -.0007458 -.0001306
math8 | .0355965 .0119779 2.97 0.003 .0121202 .0590728
mathfam | -.0005647 .0002821 -2.00 0.045 -.0011175 -.0000119
_cons | -5.362148 .6190447 -8.66 0.000 -6.575453 -4.148842
------------------------------------------------------------------------------
Description of the estimated propensity score
Estimated propensity score
-------------------------------------------------------------
Percentiles Smallest
1% .0208345 .0164257
5% .0320812 .016906
10% .0408223 .0170297 Obs 5671
25% .0672965 .017208 Sum of Wgt. 5671
50% .1056115 Mean .1043908
Largest Std. Dev. .0440799
75% .142168 .1729462
90% .1643515 .1729462 Variance .001943
95% .1647264 .1729462 Skewness -.1636008
99% .1652305 .1729462 Kurtosis 1.83253
******************************************************
Step 1: Identification of the optimal number of blocks
Use option detail if you want more detailed output
******************************************************
The final number of blocks is 6
This number of blocks ensures that the mean propensity score
is not different for treated and controls in each blocks
**********************************************************
Step 2: Test of balancing property of the propensity score
Use option detail if you want more detailed output
**********************************************************
The balancing property is satisfied
This table shows the inferior bound, the number of treated
and the number of controls for each block
Inferior |
of block | attended catholic hs?
of pscore | no yes | Total
-----------+----------------------+----------
0 | 810 31 | 841
.05 | 741 45 | 786
.075 | 928 100 | 1,028
.1 | 786 87 | 873
.125 | 810 145 | 955
.15 | 1,004 184 | 1,188
-----------+----------------------+----------
Total | 5,079 592 | 5,671
*******************************************
End of the algorithm to estimate the pscore
*******************************************
Variable means by block from Table 12.5 on page 318. Note that for Block 3, the average mathematics achievement for catholic students is listed as 49.63 in the book, but is 51.56 in the table below. Based on communication with the authors, this appears to be a typographic error in the book.
table b catholic, contents(freq mean p mean inc8 mean math8 mean math12)
--------------------------------
Number of |attended catholic hs?
block | no yes
----------+---------------------
1 | 810 31
| .03562671 .0397066
| 8.466666 9.814516
| 43.16351 44.67839
| 42.74021 45.34968
|
2 | 741 45
| .06206016 .06352629
| 18.13968 17.52778
| 47.44714 49.45711
| 47.14545 50.21756
|
3 | 928 100
| .0875975 .08860363
| 26.64197 26.565
| 48.80288 49.6273
| 48.79251 51.56
|
4 | 786 87
| .1138969 .11401803
| 33.34605 33.36207
| 52.61875 52.9077
| 52.02316 54.26402
|
5 | 810 145
| .13605543 .13692428
| 40.72839 41.46552
| 55.15296 54.78959
| 54.71558 56.54048
|
6 | 1,004 184
| .16283171 .16266777
| 57.33815 58.36956
| 58.55379 57.85957
| 56.95275 57.3175
--------------------------------
Tests for differences in academic achievement by catholic, in each block, shown in Table 12.5 on page 318. Note that the sign of the differences are reversed, but the magnitude is the same, and that the error in the mean for block 3 discussed above persists.
by b, sort: ttest math12, by(catholic)
-------------------------------------------------------------------------------------------
-> b = 1
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 810 42.74021 .2449484 6.971353 42.2594 43.22102
yes | 31 45.34968 1.310109 7.294381 42.67408 48.02528
---------+--------------------------------------------------------------------
combined | 841 42.8364 .2412525 6.996321 42.36287 43.30993
---------+--------------------------------------------------------------------
diff | -2.609468 1.277988 -5.117896 -.1010391
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.0419
Ho: diff = 0 degrees of freedom = 839
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0207 Pr(|T| > |t|) = 0.0415 Pr(T > t) = 0.9793
-------------------------------------------------------------------------------------------
-> b = 2
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 741 47.14545 .2882466 7.846452 46.57957 47.71133
yes | 45 50.21756 1.136082 7.621067 47.92793 52.50718
---------+--------------------------------------------------------------------
combined | 786 47.32134 .2804101 7.86149 46.77089 47.87178
---------+--------------------------------------------------------------------
diff | -3.072103 1.202757 -5.43311 -.7110971
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.5542
Ho: diff = 0 degrees of freedom = 784
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0054 Pr(|T| > |t|) = 0.0108 Pr(T > t) = 0.9946
-------------------------------------------------------------------------------------------
-> b = 3
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 928 48.79251 .2754558 8.391235 48.25192 49.3331
yes | 100 51.56 .8071014 8.071014 49.95854 53.16146
---------+--------------------------------------------------------------------
combined | 1028 49.06172 .2618947 8.396983 48.54781 49.57563
---------+--------------------------------------------------------------------
diff | -2.767489 .8799826 -4.49426 -1.040718
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -3.1449
Ho: diff = 0 degrees of freedom = 1026
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0009 Pr(|T| > |t|) = 0.0017 Pr(T > t) = 0.9991
-------------------------------------------------------------------------------------------
-> b = 4
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 786 52.02316 .3402795 9.539971 51.35519 52.69112
yes | 87 54.26402 .9397039 8.764975 52.39595 56.13209
---------+--------------------------------------------------------------------
combined | 873 52.24647 .3210069 9.484653 51.61644 52.87651
---------+--------------------------------------------------------------------
diff | -2.240868 1.069585 -4.340133 -.1416024
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.0951
Ho: diff = 0 degrees of freedom = 871
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0182 Pr(|T| > |t|) = 0.0365 Pr(T > t) = 0.9818
-------------------------------------------------------------------------------------------
-> b = 5
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 810 54.71558 .2588964 7.368319 54.20739 55.22377
yes | 145 56.54048 .5606502 6.751122 55.43232 57.64865
---------+--------------------------------------------------------------------
combined | 955 54.99266 .2363535 7.30405 54.52883 55.45649
---------+--------------------------------------------------------------------
diff | -1.824902 .6563147 -3.112891 -.5369135
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.7805
Ho: diff = 0 degrees of freedom = 953
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0028 Pr(|T| > |t|) = 0.0055 Pr(T > t) = 0.9972
-------------------------------------------------------------------------------------------
-> b = 6
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1004 56.95275 .2789432 8.838582 56.40537 57.50013
yes | 184 57.3175 .6020763 8.166961 56.1296 58.5054
---------+--------------------------------------------------------------------
combined | 1188 57.00924 .2534465 8.735635 56.51199 57.5065
---------+--------------------------------------------------------------------
diff | -.3647511 .7007456 -1.73959 1.010088
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -0.5205
Ho: diff = 0 degrees of freedom = 1186
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.3014 Pr(|T| > |t|) = 0.6028 Pr(T > t) = 0.6986
Weighted average ATT shown in Table 12.5 on page 318. Note that atts is part of the same user-written package as pscore and that the set seed command was used so that the results of the bootstrap can be replicated.
set seed 53156
atts math12 catholic, pscore(p) blockid(b) bootstrap
ATT estimation with the Stratification method
Analytical standard errors
---------------------------------------------------------
n. treat. n. contr. ATT Std. Err. t
---------------------------------------------------------
592 5079 1.727 0.347 4.975
---------------------------------------------------------
Bootstrapping of standard errors
command: atts math12 catholic , pscore(p) blockid(b)
statistic: atts = r(atts)
Bootstrap statistics Number of obs = 5671
Replications = 50
------------------------------------------------------------------------------
Variable | Reps Observed Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
atts | 50 1.72731 -.044933 .3138169 1.096672 2.357949 (N)
| 1.135532 2.304237 (P)
| 1.273374 2.393047 (BC)
------------------------------------------------------------------------------
Note: N = normal
P = percentile
BC = bias-corrected
ATT estimation with the Stratification method
Bootstrapped standard errors
---------------------------------------------------------
n. treat. n. contr. ATT Std. Err. t
---------------------------------------------------------
592 5079 1.727 0.314 5.504
---------------------------------------------------------
The following few examples demonstrate difference methods of analyzing the same data, treating the propensity scores as an optimal composite covariate.
Method A: Controlling for block by estimating the relationship between math12 and catholic separately in each block.
sort b
statsby _b[catholic] e(N), by(b) noisily sav(CathSlopes3,replace): regress math12 catholic
statsby: First call to regress with data as is:
. regress math12 catholic
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 1, 5669) = 90.48
Model | 8043.1077 1 8043.1077 Prob > F = 0.0000
Residual | 503934.635 5669 88.8930385 R-squared = 0.0157
-------------+------------------------------ Adj R-squared = 0.0155
Total | 511977.743 5670 90.2958982 Root MSE = 9.4283
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 3.89486 .4094621 9.51 0.000 3.092157 4.697562
_cons | 50.64465 .1322954 382.81 0.000 50.3853 50.904
------------------------------------------------------------------------------
statsby legend:
command: regress math12 catholic
_stat_1: _b[catholic]
_stat_2: e(N)
by: b
Statsby groups
running (regress math12 catholic) on group 1
. regress math12 catholic
Source | SS df MS Number of obs = 841
-------------+------------------------------ F( 1, 839) = 4.17
Model | 203.308037 1 203.308037 Prob > F = 0.0415
Residual | 40913.4431 839 48.7645329 R-squared = 0.0049
-------------+------------------------------ Adj R-squared = 0.0038
Total | 41116.7512 840 48.9485133 Root MSE = 6.9832
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 2.609468 1.277988 2.04 0.041 .1010391 5.117896
_cons | 42.74021 .2453633 174.19 0.000 42.25861 43.22181
------------------------------------------------------------------------------
running (regress math12 catholic) on group 2
. regress math12 catholic
Source | SS df MS Number of obs = 786
-------------+------------------------------ F( 1, 784) = 6.52
Model | 400.386878 1 400.386878 Prob > F = 0.0108
Residual | 48114.9879 784 61.3711581 R-squared = 0.0083
-------------+------------------------------ Adj R-squared = 0.0070
Total | 48515.3748 785 61.8030252 Root MSE = 7.834
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 3.072103 1.202757 2.55 0.011 .7110971 5.43311
_cons | 47.14545 .2877882 163.82 0.000 46.58053 47.71038
------------------------------------------------------------------------------
running (regress math12 catholic) on group 3
. regress math12 catholic
Source | SS df MS Number of obs = 1028
-------------+------------------------------ F( 1, 1026) = 9.89
Model | 691.395779 1 691.395779 Prob > F = 0.0017
Residual | 71721.6733 1026 69.904165 R-squared = 0.0095
-------------+------------------------------ Adj R-squared = 0.0086
Total | 72413.069 1027 70.5093175 Root MSE = 8.3609
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 2.767489 .8799826 3.14 0.002 1.040718 4.49426
_cons | 48.79251 .274459 177.78 0.000 48.25395 49.33108
------------------------------------------------------------------------------
running (regress math12 catholic) on group 4
. regress math12 catholic
Source | SS df MS Number of obs = 873
-------------+------------------------------ F( 1, 871) = 4.39
Model | 393.332574 1 393.332574 Prob > F = 0.0365
Residual | 78050.6082 871 89.6103423 R-squared = 0.0050
-------------+------------------------------ Adj R-squared = 0.0039
Total | 78443.9407 872 89.9586476 Root MSE = 9.4663
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 2.240868 1.069585 2.10 0.036 .1416024 4.340133
_cons | 52.02316 .3376508 154.07 0.000 51.36045 52.68586
------------------------------------------------------------------------------
running (regress math12 catholic) on group 5
. regress math12 catholic
Source | SS df MS Number of obs = 955
-------------+------------------------------ F( 1, 953) = 7.73
Model | 409.57076 1 409.57076 Prob > F = 0.0055
Residual | 50485.5136 953 52.9753553 R-squared = 0.0080
-------------+------------------------------ Adj R-squared = 0.0070
Total | 50895.0844 954 53.3491451 Root MSE = 7.2784
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.824902 .6563147 2.78 0.006 .5369135 3.112891
_cons | 54.71558 .2557375 213.95 0.000 54.21371 55.21745
------------------------------------------------------------------------------
running (regress math12 catholic) on group 6
. regress math12 catholic
Source | SS df MS Number of obs = 1188
-------------+------------------------------ F( 1, 1186) = 0.27
Model | 20.6884702 1 20.6884702 Prob > F = 0.6028
Residual | 90560.8493 1186 76.3582203 R-squared = 0.0002
-------------+------------------------------ Adj R-squared = -0.0006
Total | 90581.5377 1187 76.3113208 Root MSE = 8.7383
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | .3647511 .7007456 0.52 0.603 -1.010088 1.73959
_cons | 56.95275 .2757789 206.52 0.000 56.41168 57.49382
------------------------------------------------------------------------------
Distribution of coefficients for catholic (predicting math12) across the propensity score blocks. Note that the syntax shown below is run from a .do file, the block of syntax should be run all at once. (Not shown in text.)
preserve
use https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/CathSlopes3, clear
list
histogram _stat_1, bin(3) frequency kdensity kdenopts(gaussian)
restore
+------------------------+
| b _stat_1 _stat_2 |
|------------------------|
1. | 1 2.609468 841 |
2. | 2 3.072104 786 |
3. | 3 2.767489 1028 |
4. | 4 2.240868 873 |
5. | 5 1.824902 955 |
|------------------------|
6. | 6 .3647511 1188 |
+------------------------+
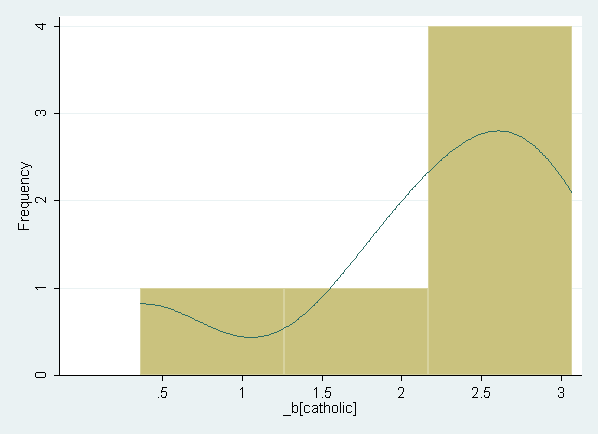
Method B: Estimate the relationship between math12 and catholic in all blocks at the same time, using fixed effects the blocks. Note that this model includes the intercept and dummy variables for blocks 2 to 6. (Not shown in text.)
xi: regress math12 catholic i.b
i.b _Ib_1-6 (naturally coded; _Ib_1 omitted)
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 6, 5664) = 326.67
Model | 131623.108 6 21937.1846 Prob > F = 0.0000
Residual | 380354.635 5664 67.1530076 R-squared = 0.2571
-------------+------------------------------ Adj R-squared = 0.2563
Total | 511977.743 5670 90.2958982 Root MSE = 8.1947
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.761271 .3595793 4.90 0.000 1.056358 2.466184
_Ib_2 | 4.449025 .4066192 10.94 0.000 3.651895 5.246154
_Ib_3 | 6.118917 .3816345 16.03 0.000 5.370767 6.867066
_Ib_4 | 9.299475 .3965866 23.45 0.000 8.522013 10.07694
_Ib_5 | 11.95377 .3897119 30.67 0.000 11.18978 12.71775
_Ib_6 | 13.96498 .3717204 37.57 0.000 13.23626 14.69369
_cons | 42.77148 .2828863 151.20 0.000 42.21691 43.32604
------------------------------------------------------------------------------
This model can also be estimated using the factor variable syntax introduced in Stata 11. (Not shown in text.)
regress math12 catholic i.b
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 6, 5664) = 326.67
Model | 131623.108 6 21937.1846 Prob > F = 0.0000
Residual | 380354.635 5664 67.1530076 R-squared = 0.2571
-------------+------------------------------ Adj R-squared = 0.2563
Total | 511977.743 5670 90.2958982 Root MSE = 8.1947
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.761271 .3595793 4.90 0.000 1.056358 2.466184
|
b |
2 | 4.449025 .4066192 10.94 0.000 3.651895 5.246154
3 | 6.118917 .3816345 16.03 0.000 5.370767 6.867066
4 | 9.299475 .3965866 23.45 0.000 8.522013 10.07694
5 | 11.95377 .3897119 30.67 0.000 11.18978 12.71775
6 | 13.96498 .3717204 37.57 0.000 13.23626 14.69369
|
_cons | 42.77148 .2828863 151.20 0.000 42.21691 43.32604
------------------------------------------------------------------------------
An equivalent model with no intercept and a fixed effect for each block. (Not shown in text.)
xi i.b, noomit
regress math12 catholic _Ib_1-_Ib_6, noconstant
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 7, 5664) =31721.90
Model | 14911547.1 7 2130221.02 Prob > F = 0.0000
Residual | 380354.635 5664 67.1530076 R-squared = 0.9751
-------------+------------------------------ Adj R-squared = 0.9751
Total | 15291901.8 5671 2696.50887 Root MSE = 8.1947
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.761271 .3595793 4.90 0.000 1.056358 2.466184
_Ib_1 | 42.77148 .2828863 151.20 0.000 42.21691 43.32604
_Ib_2 | 47.2205 .2930191 161.15 0.000 46.64607 47.79493
_Ib_3 | 48.89039 .2579679 189.52 0.000 48.38468 49.39611
_Ib_4 | 52.07095 .2796537 186.20 0.000 51.52272 52.61918
_Ib_5 | 54.72524 .270736 202.14 0.000 54.1945 55.25599
_Ib_6 | 56.73645 .2441879 232.35 0.000 56.25775 57.21515
------------------------------------------------------------------------------
This model can also be estimated using the factor variable syntax introduced in Stata 11. Note that the dummy variables do not need to be created using xi.
regress math12 catholic ibn.b, noconstant
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 7, 5664) =31721.90
Model | 14911547.1 7 2130221.02 Prob > F = 0.0000
Residual | 380354.635 5664 67.1530076 R-squared = 0.9751
-------------+------------------------------ Adj R-squared = 0.9751
Total | 15291901.8 5671 2696.50887 Root MSE = 8.1947
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.761271 .3595793 4.90 0.000 1.056358 2.466184
|
b |
1 | 42.77148 .2828863 151.20 0.000 42.21691 43.32604
2 | 47.2205 .2930191 161.15 0.000 46.64607 47.79493
3 | 48.89039 .2579679 189.52 0.000 48.38468 49.39611
4 | 52.07095 .2796537 186.20 0.000 51.52272 52.61918
5 | 54.72524 .270736 202.14 0.000 54.1945 55.25599
6 | 56.73645 .2441879 232.35 0.000 56.25775 57.21515
------------------------------------------------------------------------------
Method C: Controlling for propensities (as a linear effect). (Not shown in text.)
regress math12 catholic p
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 2, 5668) = 996.64
Model | 133204.471 2 66602.2355 Prob > F = 0.0000
Residual | 378773.272 5668 66.8266182 R-squared = 0.2602
-------------+------------------------------ Adj R-squared = 0.2599
Total | 511977.743 5670 90.2958982 Root MSE = 8.1748
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.690306 .3586574 4.71 0.000 .9872 2.393411
p | 107.6782 2.488099 43.28 0.000 102.8006 112.5559
_cons | 39.63417 .2790795 142.02 0.000 39.08707 40.18127
------------------------------------------------------------------------------
Create propensity score blocks for Table 12.6 on page 320. (Output not shown in text.)
* drop p and b from previous examples
drop p b
pscore catholic inc8 inc8sq math8 mathfam fhowfar mhowfar fight8 nohw8 ///
disrupt8 riskdrop8, logit pscore(p) blockid(b) numblo(10)
****************************************************
Algorithm to estimate the propensity score
****************************************************
The treatment is catholic
attended |
catholic |
hs? | Freq. Percent Cum.
------------+-----------------------------------
no | 5,079 89.56 89.56
yes | 592 10.44 100.00
------------+-----------------------------------
Total | 5,671 100.00
Estimation of the propensity score
Iteration 0: log likelihood = -1897.6568
Iteration 1: log likelihood = -1814.3485
Iteration 2: log likelihood = -1804.4342
Iteration 3: log likelihood = -1804.1259
Iteration 4: log likelihood = -1804.1254
Logistic regression Number of obs = 5671
LR chi2(10) = 187.06
Prob > chi2 = 0.0000
Log likelihood = -1804.1254 Pseudo R2 = 0.0493
------------------------------------------------------------------------------
catholic | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
inc8 | .0544244 .0190915 2.85 0.004 .0170058 .091843
inc8sq | -.0001894 .0001732 -1.09 0.274 -.000529 .0001501
math8 | .0215572 .0123655 1.74 0.081 -.0026787 .0457932
mathfam | -.0004537 .0002873 -1.58 0.114 -.0010169 .0001095
fhowfar | .1963326 .0866025 2.27 0.023 .0265949 .3660703
mhowfar | .0256765 .086921 0.30 0.768 -.1446855 .1960384
fight8 | -.4742975 .3246254 -1.46 0.144 -1.110552 .1619566
nohw8 | -.6880268 .1760058 -3.91 0.000 -1.032992 -.3430618
disrupt8 | .6927506 .3858711 1.80 0.073 -.0635429 1.449044
riskdrop8 | -.3033031 .0843134 -3.60 0.000 -.4685543 -.1380518
_cons | -4.981792 .703233 -7.08 0.000 -6.360104 -3.603481
------------------------------------------------------------------------------
Description of the estimated propensity score
Estimated propensity score
-------------------------------------------------------------
Percentiles Smallest
1% .0108842 .0025956
5% .0204415 .0032377
10% .0313083 .0036331 Obs 5671
25% .0595311 .0047923 Sum of Wgt. 5671
50% .1072919 Mean .1043908
Largest Std. Dev. .0530622
75% .1453336 .2551539
90% .1744188 .2571622 Variance .0028156
95% .1858031 .2619453 Skewness .0612084
99% .2138622 .262511 Kurtosis 2.084156
******************************************************
Step 1: Identification of the optimal number of blocks
Use option detail if you want more detailed output
******************************************************
The final number of blocks is 5
This number of blocks ensures that the mean propensity score
is not different for treated and controls in each blocks
**********************************************************
Step 2: Test of balancing property of the propensity score
Use option detail if you want more detailed output
**********************************************************
The balancing property is satisfied
This table shows the inferior bound, the number of treated
and the number of controls for each block
Inferior |
of block | attended catholic hs?
of pscore | no yes | Total
-----------+----------------------+----------
0 | 1,089 34 | 1,123
.05 | 1,431 110 | 1,541
.1 | 1,599 253 | 1,852
.15 | 829 160 | 989
.2 | 131 35 | 166
-----------+----------------------+----------
Total | 5,079 592 | 5,671
*******************************************
End of the algorithm to estimate the pscore
*******************************************
Distribution of estimated propensity scores based on the model for Table 12.6. (Not shown in text.)
sum p, detail
Estimated propensity score
-------------------------------------------------------------
Percentiles Smallest
1% .0108842 .0025956
5% .0204415 .0032377
10% .0313083 .0036331 Obs 5671
25% .0595311 .0047923 Sum of Wgt. 5671
50% .1072919 Mean .1043908
Largest Std. Dev. .0530622
75% .1453336 .2551539
90% .1744188 .2571622 Variance .0028156
95% .1858031 .2619453 Skewness .0612084
99% .2138622 .262511 Kurtosis 2.084156
histogram p, kdensity kdenopts(gaussian) xlabel(0(.1).3) ///
ytitle(Frequency) xtitle(Estimated Propensity Scores)
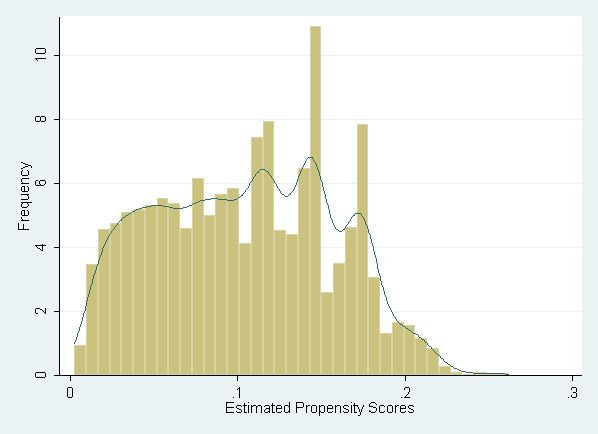
Distribution of propensity scores by catholic.
by catholic, sort: sum p, detail
-------------------------------------------------------------------------------------------
-> catholic = no
Estimated propensity score
-------------------------------------------------------------
Percentiles Smallest
1% .0104881 .0025956
5% .0195553 .0032377
10% .0297857 .0036331 Obs 5079
25% .0565767 .0047923 Sum of Wgt. 5079
50% .1008954 Mean .1012761
Largest Std. Dev. .0529831
75% .1440137 .2551539
90% .173256 .2571622 Variance .0028072
95% .1824525 .2619453 Skewness .1216262
99% .2133106 .262511 Kurtosis 2.085038
-------------------------------------------------------------------------------------------
-> catholic = yes
Estimated propensity score
-------------------------------------------------------------
Percentiles Smallest
1% .0229674 .0099903
5% .0470903 .011172
10% .0699177 .018644 Obs 592
25% .1003173 .0196516 Sum of Wgt. 592
50% .1355502 Mean .1311124
Largest Std. Dev. .0457582
75% .169457 .2266057
90% .1842547 .228063 Variance .0020938
95% .2031689 .2391276 Skewness -.3031523
99% .2224912 .2462637 Kurtosis 2.624687
histogram p, kdensity kdenopts(gaussian) by(catholic, cols(1) legend(off)) ///
xlabel(0(.1).3) ytitle(Frequency) xtitle(Estimated Propensity Scores)
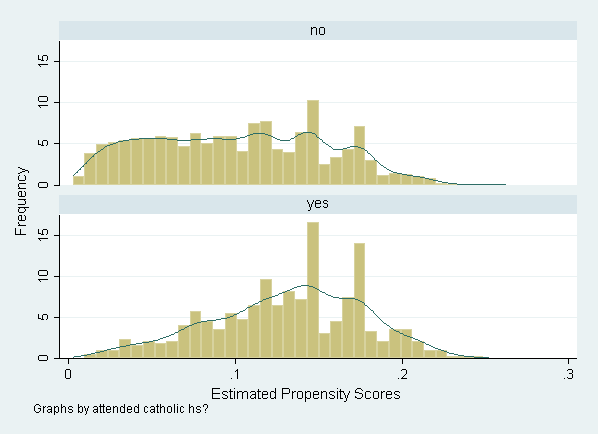
Descriptive statistics for Table 12.6 on page 320.
table b catholic, contents(freq mean p mean math12)
--------------------------------
Number of |attended catholic hs?
block | no yes
----------+---------------------
1 | 1,089 34
| .03032015 .03453844
| 43.66365 46.01353
|
2 | 1,431 110
| .07522784 .07848568
| 48.85303 51.00237
|
3 | 1,599 253
| .1270797 .12911088
| 53.62299 55.38316
|
4 | 829 160
| .17195554 .17329525
| 56.86899 57.34556
|
5 | 131 35
| .21343681 .21195736
| 52.50557 55.01257
--------------------------------
Tests for differences in academic achievement by catholic, in each block, shown in Table 12.6 on page 318. Note that the sign of the differences are reversed, but the magnitude is the same.
by b, sort: ttest math12, by(catholic)
-------------------------------------------------------------------------------------------
-> b = 1
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1089 43.66365 .2303222 7.600632 43.21172 44.11557
yes | 34 46.01353 1.288496 7.513157 43.39206 48.63499
---------+--------------------------------------------------------------------
combined | 1123 43.73479 .2269499 7.60536 43.2895 44.18008
---------+--------------------------------------------------------------------
diff | -2.349884 1.323244 -4.946197 .2464296
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -1.7759
Ho: diff = 0 degrees of freedom = 1121
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0380 Pr(|T| > |t|) = 0.0760 Pr(T > t) = 0.9620
-------------------------------------------------------------------------------------------
-> b = 2
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1431 48.85303 .2310661 8.740896 48.39977 49.3063
yes | 110 51.00236 .7979284 8.368744 49.4209 52.58383
---------+--------------------------------------------------------------------
combined | 1541 49.00646 .2223837 8.729799 48.57025 49.44266
---------+--------------------------------------------------------------------
diff | -2.149331 .8622945 -3.840727 -.4579344
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.4926
Ho: diff = 0 degrees of freedom = 1539
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0064 Pr(|T| > |t|) = 0.0128 Pr(T > t) = 0.9936
-------------------------------------------------------------------------------------------
-> b = 3
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 1599 53.62299 .2155456 8.61913 53.20021 54.04577
yes | 253 55.38316 .5098506 8.10967 54.37905 56.38727
---------+--------------------------------------------------------------------
combined | 1852 53.86344 .199154 8.570566 53.47285 54.25403
---------+--------------------------------------------------------------------
diff | -1.760173 .5786011 -2.894952 -.6253928
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -3.0421
Ho: diff = 0 degrees of freedom = 1850
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0012 Pr(|T| > |t|) = 0.0024 Pr(T > t) = 0.9988
-------------------------------------------------------------------------------------------
-> b = 4
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 829 56.86899 .2909555 8.377295 56.29789 57.44008
yes | 160 57.34556 .5922284 7.491162 56.17591 58.51521
---------+--------------------------------------------------------------------
combined | 989 56.94609 .2619749 8.238684 56.432 57.46018
---------+--------------------------------------------------------------------
diff | -.4765759 .7116066 -1.873012 .9198599
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -0.6697
Ho: diff = 0 degrees of freedom = 987
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.2516 Pr(|T| > |t|) = 0.5032 Pr(T > t) = 0.7484
-------------------------------------------------------------------------------------------
-> b = 5
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 131 52.50557 .6960753 7.966946 51.12847 53.88267
yes | 35 55.01257 1.310023 7.750203 52.35028 57.67486
---------+--------------------------------------------------------------------
combined | 166 53.03416 .6181866 7.964777 51.81358 54.25473
---------+--------------------------------------------------------------------
diff | -2.506999 1.507463 -5.483536 .4695381
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -1.6631
Ho: diff = 0 degrees of freedom = 164
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0491 Pr(|T| > |t|) = 0.0982 Pr(T > t) = 0.9509
ATT shown in Table 12.6 on page 320.
set seed 7492
atts math12 catholic, pscore(p) blockid(b) bootstrap
ATT estimation with the Stratification method
Analytical standard errors
---------------------------------------------------------
n. treat. n. contr. ATT Std. Err. t
---------------------------------------------------------
592 5079 1.564 0.353 4.424
---------------------------------------------------------
Bootstrapping of standard errors
command: atts math12 catholic , pscore(p) blockid(b)
statistic: atts = r(atts)
Bootstrap statistics Number of obs = 5671
Replications = 50
------------------------------------------------------------------------------
Variable | Reps Observed Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
atts | 50 1.563586 .0258251 .3812768 .7973821 2.329791 (N)
| .7701139 2.242676 (P)
| .605822 2.242676 (BC)
------------------------------------------------------------------------------
Note: N = normal
P = percentile
BC = bias-corrected
ATT estimation with the Stratification method
Bootstrapped standard errors
---------------------------------------------------------
n. treat. n. contr. ATT Std. Err. t
---------------------------------------------------------
592 5079 1.564 0.381 4.101
---------------------------------------------------------
Additional methods of controlling for propensity scores, using the model with additional covariates used to estimate propensity (i.e. using the propensity model from Table 12.6).
Method A: Controlling for block by estimating the relationship between math12 and catholic separately in each block.
sort b
statsby _b[catholic] e(N), by(b) noisily sav(Cathslopes4,replace): regress math12 catholic
statsby: First call to regress with data as is:
. regress math12 catholic
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 1, 5669) = 90.48
Model | 8043.1077 1 8043.1077 Prob > F = 0.0000
Residual | 503934.635 5669 88.8930385 R-squared = 0.0157
-------------+------------------------------ Adj R-squared = 0.0155
Total | 511977.743 5670 90.2958982 Root MSE = 9.4283
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 3.89486 .4094621 9.51 0.000 3.092157 4.697562
_cons | 50.64465 .1322954 382.81 0.000 50.3853 50.904
------------------------------------------------------------------------------
statsby legend:
command: regress math12 catholic
_stat_1: _b[catholic]
_stat_2: e(N)
by: b
Statsby groups
running (regress math12 catholic) on group 1
. regress math12 catholic
Source | SS df MS Number of obs = 1123
-------------+------------------------------ F( 1, 1121) = 3.15
Model | 182.062217 1 182.062217 Prob > F = 0.0760
Residual | 64716.1076 1121 57.7306936 R-squared = 0.0028
-------------+------------------------------ Adj R-squared = 0.0019
Total | 64898.1698 1122 57.8415061 Root MSE = 7.5981
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 2.349884 1.323244 1.78 0.076 -.2464296 4.946197
_cons | 43.66365 .2302446 189.64 0.000 43.21189 44.1154
------------------------------------------------------------------------------
running (regress math12 catholic) on group 2
. regress math12 catholic
Source | SS df MS Number of obs = 1541
-------------+------------------------------ F( 1, 1539) = 6.21
Model | 471.884989 1 471.884989 Prob > F = 0.0128
Residual | 116890.58 1539 75.9522939 R-squared = 0.0040
-------------+------------------------------ Adj R-squared = 0.0034
Total | 117362.465 1540 76.2093931 Root MSE = 8.7151
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 2.149331 .8622945 2.49 0.013 .4579344 3.840727
_cons | 48.85303 .2303831 212.05 0.000 48.40113 49.30493
------------------------------------------------------------------------------
running (regress math12 catholic) on group 3
. regress math12 catholic
Source | SS df MS Number of obs = 1852
-------------+------------------------------ F( 1, 1850) = 9.25
Model | 676.765989 1 676.765989 Prob > F = 0.0024
Residual | 135287.688 1850 73.1284801 R-squared = 0.0050
-------------+------------------------------ Adj R-squared = 0.0044
Total | 135964.454 1851 73.4545944 Root MSE = 8.5515
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.760173 .5786011 3.04 0.002 .6253928 2.894952
_cons | 53.62299 .2138548 250.74 0.000 53.20357 54.04241
------------------------------------------------------------------------------
running (regress math12 catholic) on group 4
. regress math12 catholic
Source | SS df MS Number of obs = 989
-------------+------------------------------ F( 1, 987) = 0.45
Model | 30.4608727 1 30.4608727 Prob > F = 0.5032
Residual | 67030.949 987 67.9138288 R-squared = 0.0005
-------------+------------------------------ Adj R-squared = -0.0006
Total | 67061.4099 988 67.875921 Root MSE = 8.241
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | .4765759 .7116066 0.67 0.503 -.9198599 1.873012
_cons | 56.86899 .2862212 198.69 0.000 56.30731 57.43066
------------------------------------------------------------------------------
running (regress math12 catholic) on group 5
. regress math12 catholic
Source | SS df MS Number of obs = 166
-------------+------------------------------ F( 1, 164) = 2.77
Model | 173.595927 1 173.595927 Prob > F = 0.0982
Residual | 10293.6209 164 62.7659812 R-squared = 0.0166
-------------+------------------------------ Adj R-squared = 0.0106
Total | 10467.2168 165 63.4376779 Root MSE = 7.9225
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 2.506999 1.507463 1.66 0.098 -.4695381 5.483536
_cons | 52.50557 .6921919 75.85 0.000 51.13882 53.87233
------------------------------------------------------------------------------
Distribution of coefficients for catholic (predicting math12) across the propensity score blocks. Note that the syntax shown below is run from a .do file, the block of syntax should be run all at once. (Not shown in text.)
preserve
use https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/CathSlopes4, clear
list
histogram _stat_1, bin(3) frequency kdensity kdenopts(gaussian)
restore
+------------------------+
| b _stat_1 _stat_2 |
|------------------------|
1. | 1 2.349884 1123 |
2. | 2 2.149331 1541 |
3. | 3 1.760173 1852 |
4. | 4 .4765759 989 |
5. | 5 2.506999 166 |
+------------------------+
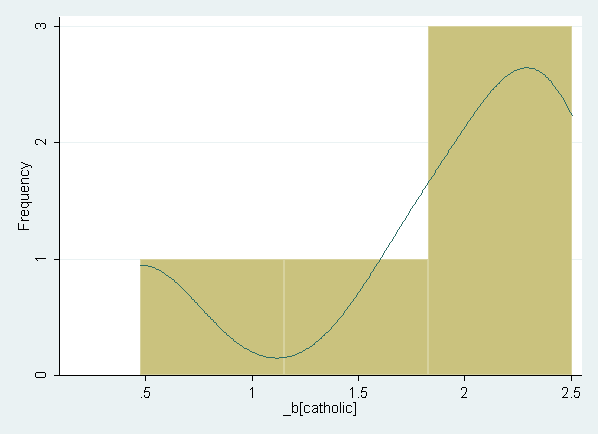
Method B: Estimate the relationship between math12 and catholic in all blocks at the same time, using fixed effects the blocks. Note that this model includes the intercept and dummy variables for blocks 2 to 6. (Not shown in text.)
xi: regress math12 catholic i.b
i.b _Ib_1-5 (naturally coded; _Ib_1 omitted)
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 5, 5665) = 337.52
Model | 117512.027 5 23502.4055 Prob > F = 0.0000
Residual | 394465.715 5665 69.6320768 R-squared = 0.2295
-------------+------------------------------ Adj R-squared = 0.2288
Total | 511977.743 5670 90.2958982 Root MSE = 8.3446
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.580998 .367602 4.30 0.000 .8603572 2.301639
_Ib_2 | 5.206677 .32775 15.89 0.000 4.564162 5.849193
_Ib_3 | 9.960542 .318012 31.32 0.000 9.337117 10.58397
_Ib_4 | 13.00339 .3670815 35.42 0.000 12.28377 13.72301
_Ib_5 | 9.013889 .6970521 12.93 0.000 7.6474 10.38038
_cons | 43.68692 .2492575 175.27 0.000 43.19828 44.17556
------------------------------------------------------------------------------
This model can also be estimated using the factor variable syntax introduced in Stata 11. (Not shown in text.)
regress math12 catholic i.b
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 5, 5665) = 337.52
Model | 117512.027 5 23502.4055 Prob > F = 0.0000
Residual | 394465.715 5665 69.6320768 R-squared = 0.2295
-------------+------------------------------ Adj R-squared = 0.2288
Total | 511977.743 5670 90.2958982 Root MSE = 8.3446
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.580998 .367602 4.30 0.000 .8603572 2.301639
|
b |
2 | 5.206677 .32775 15.89 0.000 4.564162 5.849193
3 | 9.960542 .318012 31.32 0.000 9.337117 10.58397
4 | 13.00339 .3670815 35.42 0.000 12.28377 13.72301
5 | 9.013889 .6970521 12.93 0.000 7.6474 10.38038
|
_cons | 43.68692 .2492575 175.27 0.000 43.19828 44.17556
------------------------------------------------------------------------------
An equivalent model with no intercept and a fixed effect for each block. (Not shown in text.)
xi i.b, noomit
regress math12 catholic _Ib_1-_Ib_5, noconstant
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 6, 5665) =35657.50
Model | 14897436.1 6 2482906.01 Prob > F = 0.0000
Residual | 394465.715 5665 69.6320768 R-squared = 0.9742
-------------+------------------------------ Adj R-squared = 0.9742
Total | 15291901.8 5671 2696.50887 Root MSE = 8.3446
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.580998 .367602 4.30 0.000 .8603572 2.301639
_Ib_1 | 43.68692 .2492575 175.27 0.000 43.19828 44.17556
_Ib_2 | 48.8936 .2141841 228.28 0.000 48.47372 49.31348
_Ib_3 | 53.64747 .2003001 267.84 0.000 53.2548 54.04013
_Ib_4 | 56.69031 .2719252 208.48 0.000 56.15724 57.22339
_Ib_5 | 52.70081 .6522864 80.79 0.000 51.42208 53.97954
------------------------------------------------------------------------------
This model can also be estimated using the factor variable syntax introduced in Stata 11. Note that the dummy variables do not need to be created using xi.
regress math12 catholic ibn.b, noconstant
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 6, 5665) =35657.50
Model | 14897436.1 6 2482906.01 Prob > F = 0.0000
Residual | 394465.715 5665 69.6320768 R-squared = 0.9742
-------------+------------------------------ Adj R-squared = 0.9742
Total | 15291901.8 5671 2696.50887 Root MSE = 8.3446
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.580998 .367602 4.30 0.000 .8603572 2.301639
|
b |
1 | 43.68692 .2492575 175.27 0.000 43.19828 44.17556
2 | 48.8936 .2141841 228.28 0.000 48.47372 49.31348
3 | 53.64747 .2003001 267.84 0.000 53.2548 54.04013
4 | 56.69031 .2719252 208.48 0.000 56.15724 57.22339
5 | 52.70081 .6522864 80.79 0.000 51.42208 53.97954
------------------------------------------------------------------------------
Method C: Controlling for propensities (as a linear effect). (Not shown in text.)
regress math12 catholic p
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 2, 5668) = 802.96
Model | 113033.68 2 56516.8401 Prob > F = 0.0000
Residual | 398944.063 5668 70.3853321 R-squared = 0.2208
-------------+------------------------------ Adj R-squared = 0.2205
Total | 511977.743 5670 90.2958982 Root MSE = 8.3896
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.438686 .3698603 3.89 0.000 .7136181 2.163753
p | 82.32179 2.131477 38.62 0.000 78.14328 86.5003
_cons | 42.30742 .2458801 172.07 0.000 41.8254 42.78944
------------------------------------------------------------------------------
Controlling for selection using nearest-neighbor matching (with random draws). Discussed on page 323. The command attnd is part of the same user-written package as pscore and atts.
attnd math12 catholic, pscore(p) comsup detail matchvar(neighbor) matchdta(pickdat3) id(id)
****************************************************************
Estimation of the ATT with the nearest neighbor matching method
Random draw version
****************************************************************
Note: the common support option has been selected
The region of common support is [.00999032, .24626373]
The outcome is math12
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
math12 | 5617 51.14784 9.475516 29.88 71.37
The treatment is catholic
attended |
catholic |
hs? | Freq. Percent Cum.
------------+-----------------------------------
no | 5,025 89.46 89.46
yes | 592 10.54 100.00
------------+-----------------------------------
Total | 5,617 100.00
The distribution of the pscore is
Estimated propensity score
-------------------------------------------------------------
Percentiles Smallest
1% .0133107 .0099903
5% .0224748 .0100709
10% .0323934 .0101176 Obs 5617
25% .0604995 .0102946 Sum of Wgt. 5617
50% .107828 Mean .1049281
Largest Std. Dev. .0522626
75% .145359 .2322851
90% .1742154 .2384602 Variance .0027314
95% .1851969 .2391276 Skewness .0475229
99% .2127406 .2462637 Kurtosis 2.030977
The program is searching the nearest neighbor of each treated unit.
This operation may take a while.
****************************************************
Forward search
****************************************************
Backward search
****************************************************
Choice between backward or forward match
****************************************************
Display of final results
****************************************************
The number of treated is
592
The number of treated which have been matched is
592
Average absolute pscore difference between treated and controls
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
PSDIF | 592 .0000432 .0003268 0 .0078036
Average outcome of the matched treated
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
math12 | 592 54.53951 8.463153 32.92 71.08
Average outcome of the matched controls
Variable | Obs Weight Mean Std. Dev. Min Max
-------------+-----------------------------------------------------------------
math12 | 553 592 53.61822 8.913623 32.05 70.79
(553 real changes made)
(592 real changes made)
ATT estimation with Nearest Neighbor Matching method
(random draw version)
Analytical standard errors
---------------------------------------------------------
n. treat. n. contr. ATT Std. Err. t
---------------------------------------------------------
592 553 0.921 0.537 1.716
---------------------------------------------------------
Note: the numbers of treated and controls refer to actual
nearest neighbour matches
*****************************************************************************
End of the estimation with the nearest neighbor matching (random draw) method
*****************************************************************************
Inspect the neighbors based on the above model and estimate ATE. Note that the syntax shown below is run from a .do file, the block of syntax should be run all at once. The syntax is shown twice, once as a single block, then with the output. (Discussed on page 323.)
* Syntax alone
preserve
use https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/pickdat3, clear
merge id using "https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/catholic.dta" , ///
unique update
sort p catholic
list id p catholic faminc8 math8 fhowfar mhowfar fight8 nohw8 disrupt8 riskdrop8 ///
if p<.012 & neighbor==1
* Estimate ATE directly
ttest math12 if neighbor==1, by(catholic)
restore
* Syntax with output
preserve
use https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/pickdat3, clear
merge id using "https://stats.idre.ucla.edu/stat/stata/examples/methods_matter/chapter12/catholic.dta" , ///
unique update
id was float now double
sort p catholic
list id p catholic faminc8 math8 fhowfar mhowfar fight8 nohw8 disrupt8 riskdrop8 ///
if p<.012 & neighbor==1
+----------------------------------------------------------------------------------+
1. | id | p | catholic | faminc8 | math8 | fhowfar | mhowfar |
| 1485802 | .0099903 | yes | $3000-$4999 | 42.02 | coll <4 | postsec ed |
|----------------------------------------------------------------------------------|
| fight8 | nohw8 | disrupt8 | riskdr~8 |
| never | yes | no | 3 |
+----------------------------------------------------------------------------------+
+----------------------------------------------------------------------------------+
2. | id | p | catholic | faminc8 | math8 | fhowfar | mhowfar |
| 709436 | .0100709 | no | $3000-$4999 | 52.16 | hs grad | hs grad |
|----------------------------------------------------------------------------------|
| fight8 | nohw8 | disrupt8 | riskdr~8 |
| never | yes | no | 2 |
+----------------------------------------------------------------------------------+
+----------------------------------------------------------------------------------+
14. | id | p | catholic | faminc8 | math8 | fhowfar | mhowfar |
| 6873825 | .0111274 | no | $5000-$7499 | 39.05 | postsec ed | postsec ed |
|----------------------------------------------------------------------------------|
| fight8 | nohw8 | disrupt8 | riskdr~8 |
| never | yes | no | 4 |
+----------------------------------------------------------------------------------+
+----------------------------------------------------------------------------------+
15. | id | p | catholic | faminc8 | math8 | fhowfar | mhowfar |
| 1485892 | .011172 | yes | $10000-$14999 | 42.36 | hs grad | junior coll |
|----------------------------------------------------------------------------------|
| fight8 | nohw8 | disrupt8 | riskdr~8 |
| never | yes | no | 2 |
+----------------------------------------------------------------------------------+
* Estimate ATE directly
ttest math12 if neighbor==1, by(catholic)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
no | 553 53.50092 .3811649 8.963455 52.75221 54.24963
yes | 592 54.53951 .3478334 8.463153 53.85637 55.22265
---------+--------------------------------------------------------------------
combined | 1145 54.0379 .2577003 8.720023 53.53229 54.54352
---------+--------------------------------------------------------------------
diff | -1.038588 .5150099 -2.049059 -.0281169
------------------------------------------------------------------------------
diff = mean(no) - mean(yes) t = -2.0166
Ho: diff = 0 degrees of freedom = 1143
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0220 Pr(|T| > |t|) = 0.0440 Pr(T > t) = 0.9780
restore
Model estimated using inverse propensity score weighting, discussed starting on page 327. Inverse probability weights are calculated based on the propensity scores for the previous model.
gen pscorewgt=1/p replace pscorewgt=1/(1-p) if catholic==0 (5079 real changes made)
Estimate the ATE using the Imbens and Wooldridge method detailed in footnote 29 on page 327. Estimating the ATE "by hand."
gen pmath12=pscorewgt*math12
total pmath12 if catholic==0
Total estimation Number of obs = 5079
--------------------------------------------------------------
| Total Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
pmath12 | 288700 894.6781 286946.1 290454
--------------------------------------------------------------
total pmath12 if catholic==1
Total estimation Number of obs = 592
--------------------------------------------------------------
| Total Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
pmath12 | 297285.7 8240.164 281102.1 313469.3
--------------------------------------------------------------
total pscorewgt if catholic==0
Total estimation Number of obs = 5079
--------------------------------------------------------------
| Total Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
pscorewgt | 5671.273 4.753054 5661.955 5680.591
--------------------------------------------------------------
total pscorewgt if catholic==1
Total estimation Number of obs = 592
--------------------------------------------------------------
| Total Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
pscorewgt | 5675.911 192.6692 5297.512 6054.311
--------------------------------------------------------------
* calculate the ATE
display 297285.7/5675.911 - 288700/5671.273
1.4710589
Estimate the ATE using analytic weights. (Note this is the same Imbens and Wooldridge estimator as above, with a different method of calculation.)
sum math12 if catholic==0 [aw=pscorewgt]
Variable | Obs Weight Mean Std. Dev. Min Max
-------------+-----------------------------------------------------------------
math12 | 5079 5671.27272 50.90568 9.525339 29.88 71.37
sum math12 if catholic==1 [aw=pscorewgt]
Variable | Obs Weight Mean Std. Dev. Min Max
-------------+-----------------------------------------------------------------
math12 | 592 5675.9113 52.37674 9.03198 32.92 71.08
display 52.37674-50.90568
1.47106
Estimate the ATE using WLS with analytic weights. (Note this is the same Imbens and Wooldridge estimator as above, with a different method of calculation.)
regress math12 catholic [aw=pscorewgt]
(sum of wgt is 1.1347e+04)
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 1, 5669) = 35.63
Model | 3068.00754 1 3068.00754 Prob > F = 0.0000
Residual | 488129.279 5669 86.105006 R-squared = 0.0062
-------------+------------------------------ Adj R-squared = 0.0061
Total | 491197.287 5670 86.6309148 Root MSE = 9.2793
------------------------------------------------------------------------------
math12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
catholic | 1.471053 .2464418 5.97 0.000 .9879331 1.954174
_cons | 50.90568 .1742963 292.06 0.000 50.564 51.24737
------------------------------------------------------------------------------
Estimate the ATE using WLS by transformation. (Note this is the same Imbens and Wooldridge estimator as above, with a different method of calculation.)
gen w=sqrt(pscorewgt)
gen wmath12 = w*math12
gen wcatholic = w*catholic
regress wmath12 w wcatholic, noconstant
Source | SS df MS Number of obs = 5671
-------------+------------------------------ F( 2, 5669) =87838.97
Model | 30267327.8 2 15133663.9 Prob > F = 0.0000
Residual | 976704.778 5669 172.288724 R-squared = 0.9687
-------------+------------------------------ Adj R-squared = 0.9687
Total | 31244032.6 5671 5509.43971 Root MSE = 13.126
------------------------------------------------------------------------------
wmath12 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
w | 50.90568 .1742963 292.06 0.000 50.564 51.24737
wcatholic | 1.471053 .2464418 5.97 0.000 .987933 1.954173
------------------------------------------------------------------------------
Kernel-density of inc8 without weighting. (Note shown in text.)
twoway kdensity inc8 if catholic==1 || /// kdensity inc8 if catholic==0, /// legend(off) scheme(lean1)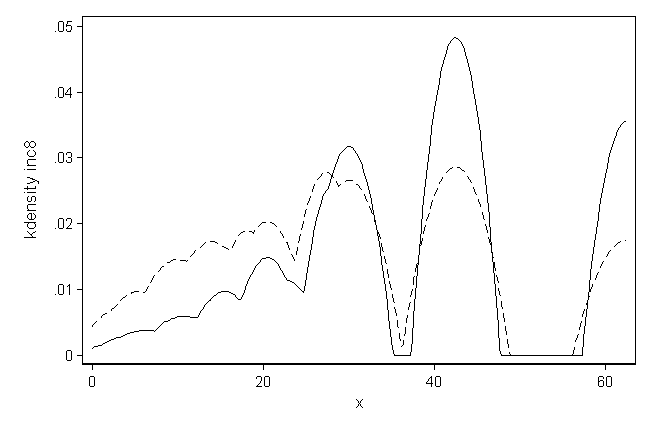
Kernel-density of inc8 with inverse propensity weighting. (Note shown in text.)
twoway kdensity inc8 if catholic==1 [aw=pscorewgt] || /// kdensity inc8 if catholic==0 [aw=pscorewgt], /// legend(off) scheme(lean1)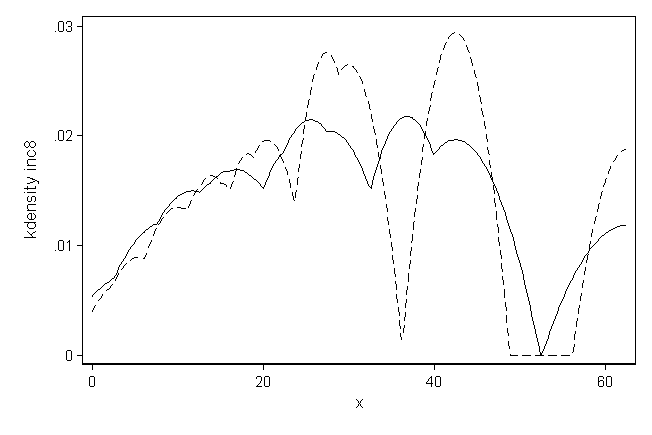
Figure 13.3, Part A on page 327.
twoway kdensity math8 if catholic==1 || /// kdensity math8 if catholic==0, /// legend(off) scheme(lean1)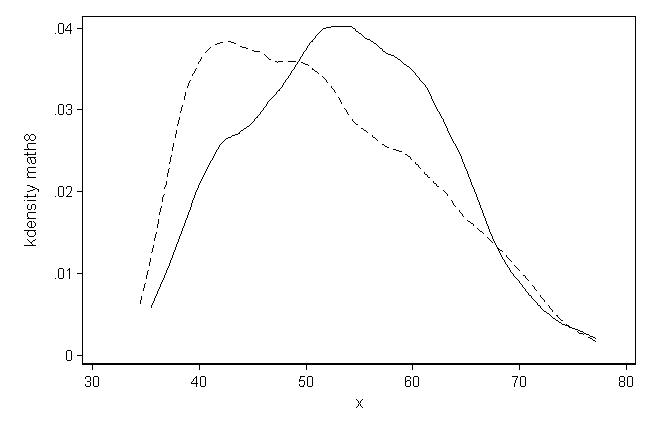
Figure 13.3, Part B on page 327.
twoway kdensity math8 if catholic==1 [aw=pscorewgt] || /// kdensity math8 if catholic==0 [aw=pscorewgt], /// legend(off) scheme(lean1)