The data set used in this chapter is popular.dta. The programs we use in this chapter are gllamm and gllapred. You can find the programs and download them by issuing command search gllamm and search gllapred (see How can I use the search command to search for programs and get additional help? for more information about using search). For more information see http://www.gllamm.org .
Table 2.1 on page 17.
Part1: Intercept only. (M0). The deviance is obtained by multiplying the log likelihood by -2.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/popular.dta, clear
gllamm popular, i(school) adapt
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 5.8576802
gllamm model
log likelihood = -2556.3612
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | 5.307604 .0950217 55.86 0.000 5.121365 5.493843
------------------------------------------------------------------------------
Variance at level 1
-----------------------------------------------------------------------------
.63867681 (.02072164)
Variances and covariances of random effects
-----------------------------------------------------------------------------
***level 2 (school)
var(1): .87068762 (.12771943)
-----------------------------------------------------------------------------
di 2*2556.3612
5112.7224
Part 2: The variable sex is included as a random effect and teacher experience (texp) as fixed effect (M1).
eq sch_s: sex gen cons = 1 eq sch_c: cons gllamm popular texp sex, i(school) adapt nrf(2) eq(sch_c sch_s)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 40.498391
gllamm model
log likelihood = -2130.5659
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
texp | .1084215 .0106385 10.19 0.000 .0875704 .1292726
sex | .8432452 .0587151 14.36 0.000 .7281656 .9583247
_cons | 3.339099 .1651731 20.22 0.000 3.015366 3.662832
------------------------------------------------------------------------------
Variance at level 1
-----------------------------------------------------------------------------
.39241954 (.0130915)
Variances and covariances of random effects
-----------------------------------------------------------------------------
***level 2 (school)
var(1): .40328261 (.06227253)
cov(1,2): .02171346 (.04195842) cor(1,2): .06576171
var(2): .27033508 (.04961092)
-----------------------------------------------------------------------------
Table 2.2 on page 20.
Part 1: Same as the last model appeared in table 2.1.Part 2: Cross-level interaction of variable sex and texp is included. Notice this model takes very LONG time to run.
gen gxt = sex*texp eq sch_s: sex gen cons = 1 eq sch_c: cons gllamm popular texp sex gxt, i(school) adapt nrf(2) eq(sch_c sch_s)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 45.72526
gllamm model
log likelihood = -2122.9085
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
texp | .1102169 .0099904 11.03 0.000 .090636 .1297977
sex | 1.32949 .130912 10.16 0.000 1.072907 1.586073
gxt | -.034026 .0083388 -4.08 0.000 -.0503697 -.0176822
_cons | 3.313841 .1566164 21.16 0.000 3.006879 3.620804
------------------------------------------------------------------------------
Variance at level 1
-----------------------------------------------------------------------------
.39236316 (.01308622)
Variances and covariances of random effects
-----------------------------------------------------------------------------
***level 2 (school)
var(1): .40543808 (.0627154)
cov(1,2): .02386608 (.03657119) cor(1,2): .0795611
var(2): .22194032 (.04304873)
-----------------------------------------------------------------------------
Table 2.3 on page 21.
Part 1: M1 from table 2.2.
Part 2: Standardized variables. We first created standardized variables: zpopular, zsex and ztexp.
egen zsex = std(sex) egen ztexp = std(texp) eq sch_zs: zsex egen zpop = std(popular) gllamm zpop ztexp zsex , i(school) adapt nrf(2) eq(sch_c sch_zs)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 3.6590204
gllamm model
log likelihood = -1723.1996
------------------------------------------------------------------------------
zpop | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ztexp | .5790798 .0583238 9.93 0.000 .4647672 .6933923
zsex | .3438637 .0242194 14.20 0.000 .2963946 .3913328
_cons | -.0097627 .0581163 -0.17 0.867 -.1236685 .1041431
------------------------------------------------------------------------------
Variance at level 1
-----------------------------------------------------------------------------
.26115453 (.00870857)
Variances and covariances of random effects
-----------------------------------------------------------------------------
***level 2 (school)
var(1): .32405547 (.04869577)
cov(1,2): .05071581 (.01594587) cor(1,2): .42065269
var(2): .04485594 (.00834557)
-----------------------------------------------------------------------------
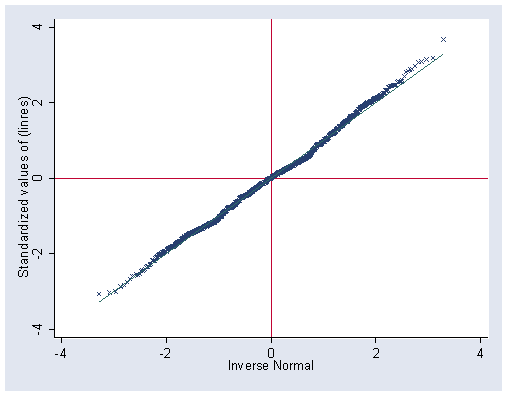
Figure 2.1 on page 23 based on model M1 from Table 2.2. After running M1, command gllapred can be used to generate various predicted values. Here we use gllapred first to generate the predicted value using only the fixed part of the equation (xb) and then generate the posterior means (empirical Bayes predictions) and standard deviations of the random effects (u). postm1 corresponds to the random effect of intercept and postm2 corresponds to the random effect of variable sex. Therefore, the prediction using both the fixed effect and the random effect will be our new variable linp below. We can then use it to generate the standardized residuals, which is stdres.
gllapred p, xb gllapred post, u adapt gen linp = p + postm1 + postm2*sex gen linres = popular - linp egen stdres = std(linres) qnorm stdres, yline(0) xline(0) msymbol(X)
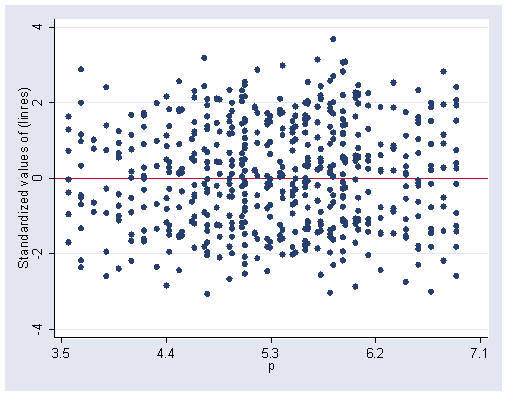
Figure 2.2 on page 24. Based on what we have generated for figure 2.1, we can do the following:
graph twoway scatter stdres p, yline(0) xlabel(3.5(.9)7.1)
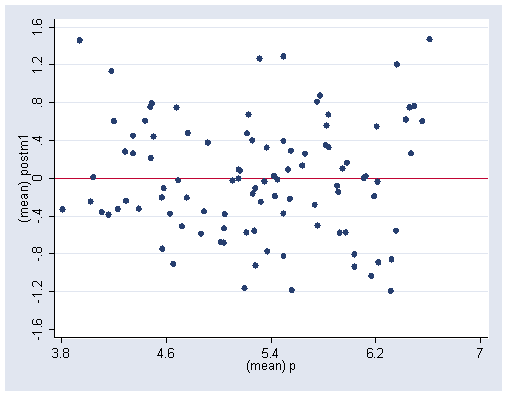
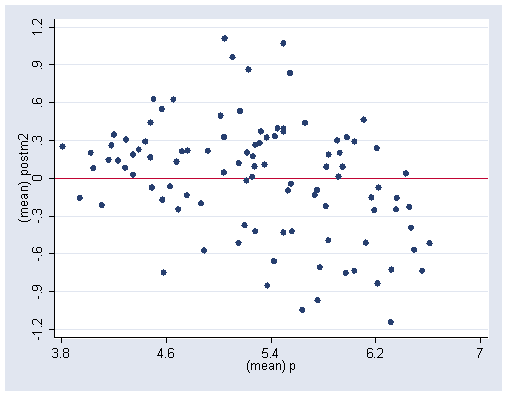
Figure 2.3 on page 24.
collapse (mean) p postm1 posts1 postm2 posts2, by(school) graph twoway scatter postm1 p, yline(0) ylabel(-1.6(.4) 1.6) xlabel(3.8(.8) 7.0)
. graph twoway scatter postm2 p, yline(0) ylabel(-1.2(.3) 1.2)xlabel(3.8(.8) 7.0)
Figure 2.4 on page 25.
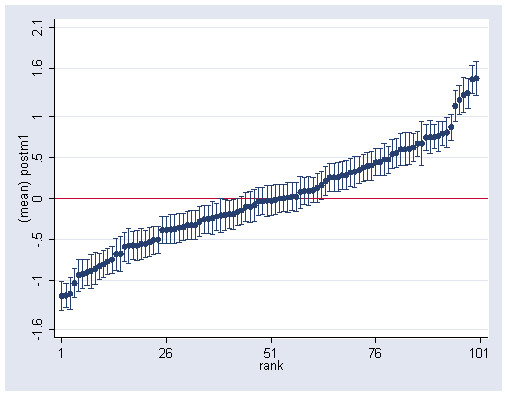
sort postm1 gen rank=_n serrbar postm1 posts1 rank, yline(0) ylabel(-1.6 -1.0 -.5 0 .5 1 1.6 2.1) xlabel(1(25)101)
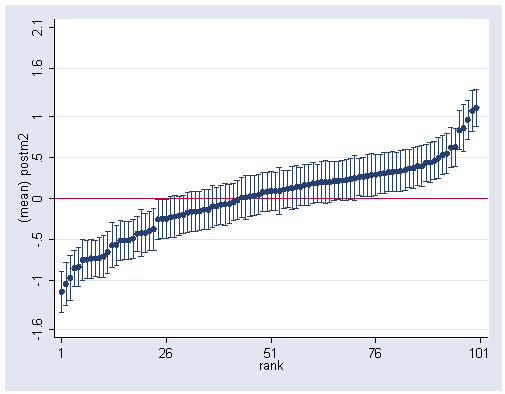
drop rank sort postm2 gen rank=_n serrbar postm2 posts2 rank, yline(0) ylabel(-1.6 -1.0 -.5 0 .5 1 1.6 2.1) xlabel(1(25)101)
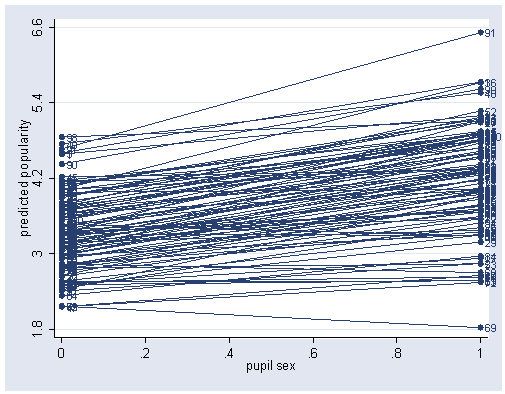
Figure 2.6 on page 28.
gen p26 = linp - .1084215 *texp label variable p26 "predicted popularity" sort school sex graph twoway scatter p26 sex, mlabel(school) connect(L) ylabel(1.8(1.2)6.6)