The data set used in this chapter is popular.dta.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/popular.dta, clear
The programs we use in this chapter are gllamm and gllapred. You can find the programs and download them by issuing command search gllamm and search gllapred (see How can I use the search command to search for programs and get additional help? for more information about using search). For more information, see http://www.gllamm.org.
Table 4.1 on page 57.
Part 1: The variable sex is a fixed effect, not centered.
gen cons = 1
eq sch_c: cons
gllamm popular sex, i(school) adapt nrf(1) eq(sch_c )
Iteration 0: log likelihood = -2242.4431 (not concave)
Iteration 1: log likelihood = -2242.4431
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 5.8538169
gllamm model
log likelihood = -2242.4431
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sex | .8437617 .0309587 27.25 0.000 .7830838 .9044396
_cons | 4.897324 .0948272 51.64 0.000 4.711466 5.083182
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.45976423 (.01491828)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .85332444 (.12397587)
------------------------------------------------------------------------------
Part 2: The variable sex is a fixed effect, raw centered. We first created a centered variable csex for sex.
sum sex
Variable | Obs Mean Std. Dev. Min Max
-------------+-----------------------------------------------------
sex | 2000 .487 .499956 0 1
gen csex = sex - .487
gllamm popular csex, i(school) adapt nrf(1) eq(sch_c )
Iteration 0: log likelihood = -2242.4431
Iteration 1: log likelihood = -2242.4431 (backed up)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 5.770973
gllamm model
log likelihood = -2242.4431
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
csex | .8437679 .0309587 27.25 0.000 .78309 .9044458
_cons | 5.308208 .0936253 56.70 0.000 5.124706 5.49171
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.45976398 (.01491826)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .8533484 (.12398179)
------------------------------------------------------------------------------
Part 3: The variable sex is included as a random effect.
eq sch_s: sex
gllamm popular sex, i(school) adapt nrf(2) eq(sch_c sch_s) nip(10)
overflow at level 1 ( 2000 missing values)
Iteration 0: log likelihood = -2164.81 (not concave)
Iteration 1: log likelihood = -2164.81
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 6.0668644
gllamm model
log likelihood = -2164.81
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sex | .8431011 .0595275 14.16 0.000 .7264294 .9597729
_cons | 4.889713 .0985275 49.63 0.000 4.696602 5.082823
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.39276323 (.01310068)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .93057658 (.13755058)
cov(2,1): -.14062495 (.06150458) cor(2,1): -.27993848
var(2): .27117361 (.05062667)
------------------------------------------------------------------------------
Part 4: The variable sex is centered and is a random effect.
eq sch_cs: csex
gllamm popular csex, i(school) adapt nrf(2) eq(sch_c sch_cs) nip(10)
overflow at level 1 ( 2000 missing values)
overflow at level 1 ( 2000 missing values)
overflow at level 1 ( 2000 missing values)
overflow at level 1 ( 2000 missing values)
overflow at level 1 ( 2000 missing values)
Iteration 0: log likelihood = -2164.8092
Iteration 1: log likelihood = -2164.8091
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 5.6405438
gllamm model
log likelihood = -2164.8091
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
csex | .8432686 .0594125 14.19 0.000 .7268222 .959715
_cons | 5.301004 .0938812 56.46 0.000 5.117 5.485008
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.3926911 (.01309742)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .86073658 (.12487103)
cov(2,1): -.00787439 (.0558919) cor(2,1): -.01633958
var(2): .26982466 (.05030262)
------------------------------------------------------------------------------
Table 4.2 on page 60.
Part 1: No interaction, no centering.
eq sch_c: cons
eq sch_s: sex
gllamm popular texp sex, i(school) adapt nrf(2) eq(sch_c sch_s)
Iteration 0: log likelihood = -2130.5924
Iteration 1: log likelihood = -2130.5924 (backed up)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 40.750777
gllamm model
log likelihood = -2130.5924
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
texp | .1086393 .0109591 9.91 0.000 .0871599 .1301187
sex | .8432268 .0596367 14.14 0.000 .726341 .9601127
_cons | 3.335057 .1703028 19.58 0.000 3.00127 3.668844
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.39215591 (.01307054)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .40612555 (.06376658)
cov(2,1): .02252195 (.0433015) cor(2,1): .06767289
var(2): .27272336 (.05087203)
------------------------------------------------------------------------------
Part 2: With interaction, but no centering.
gen gxt = sex*texp
gllamm popular texp sex gxt, i(school) adapt nrf(2) eq(sch_c sch_s)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 45.72526
gllamm model
log likelihood = -2122.9085
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
texp | .1102169 .0099904 11.03 0.000 .090636 .1297977
sex | 1.32949 .130912 10.16 0.000 1.072907 1.586073
gxt | -.034026 .0083388 -4.08 0.000 -.0503697 -.0176822
_cons | 3.313841 .1566164 21.16 0.000 3.006879 3.620804
------------------------------------------------------------------------------
Variance at level 1
-----------------------------------------------------------------------------
.39236316 (.01308622)
Variances and covariances of random effects
-----------------------------------------------------------------------------
***level 2 (school)
var(1): .40543808 (.0627154)
cov(1,2): .02386608 (.03657119) cor(1,2): .0795611
var(2): .22194032 (.04304873)
-----------------------------------------------------------------------------
Part 3: Centering, but no interaction. We first created new variables csex and ctexp.
sum sex texp
Variable | Obs Mean Std. Dev. Min Max
-------------+-----------------------------------------------------
sex | 2000 .487 .499956 0 1
texp | 2000 14.263 6.551816 2 25
gen csex = sex - .487
gen ctexp = texp - 14.263
eq sch_cs: csex
gllamm popular ctexp csex, i(school) adapt nrf(2) eq(sch_c sch_cs)
Iteration 0: log likelihood = -2130.5886
Iteration 1: log likelihood = -2130.5886
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 7.6882806
gllamm model
log likelihood = -2130.5886
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ctexp | .1083871 .0109338 9.91 0.000 .0869572 .129817
csex | .8431748 .0595189 14.17 0.000 .7265198 .9598297
_cons | 5.296027 .0713829 74.19 0.000 5.15612 5.435935
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.39250908 (.01308857)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .48895935 (.07367622)
cov(2,1): .15310509 (.04822943) cor(2,1): .42040184
var(2): .27125472 (.05053632)
------------------------------------------------------------------------------
Part 4: Centering and with interaction. First we created the interaction term of centered variable csex and ctexp.
gen csxctp = csex*ctexp
gllamm popular ctexp csex csxctp, i(school) adapt nrf(2) eq(sch_c sch_cs)
Iteration 0: log likelihood = -2122.9262 (not concave)
Iteration 1: log likelihood = -2122.9262
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 10.144082
gllamm model
log likelihood = -2122.9262
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ctexp | .0937768 .0107735 8.70 0.000 .0726611 .1148926
csex | .8445003 .0551347 15.32 0.000 .7364384 .9525622
csxctp | -.0339454 .0083838 -4.05 0.000 -.0503773 -.0175135
_cons | 5.296914 .0708369 74.78 0.000 5.158076 5.435751
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.39248971 (.01308628)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .48124165 (.07133837)
cov(2,1): .13159538 (.04146938) cor(2,1): .40346808
var(2): .22105469 (.04324507)
------------------------------------------------------------------------------
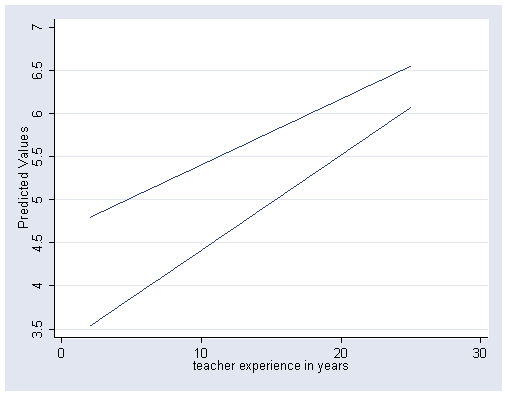
Figure 4.3on page 61. Regression lines for popularity of girls and boys, predicted by teacher experience texp. This uses model in Part 2 of table 4.2. We use the model to obtain the predicted values by the variables sex, texp and their interaction.
gen gxt = sex*texp
gllamm popular texp sex gxt, i(school) adapt nrf(2) eq(sch_c sch_s)
Iteration 0: log likelihood = -2122.9298
Iteration 1: log likelihood = -2122.9298 (backed up)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 45.868482
gllamm model
log likelihood = -2122.9298
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
texp | .1102158 .0101679 10.84 0.000 .090287 .1301445
sex | 1.329446 .1324726 10.04 0.000 1.069804 1.589087
gxt | -.0340267 .0084205 -4.04 0.000 -.0505305 -.0175229
_cons | 3.313861 .1600069 20.71 0.000 3.000253 3.627468
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.3923864 (.01307988)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .40632752 (.06373128)
cov(2,1): .02339192 (.03724399) cor(2,1): .07758212
var(2): .22373414 (.04387262)
------------------------------------------------------------------------------
gllapred p, xb
label variable p "Predicted Values"
sort sex texp
graph twoway scatter p texp, connect(L) msymbol(i) ylabel(3.5(.5)7) xlabel(0(10)30)
Table 4.3
Part 1: Intercept only. This has been done in Chapter 2.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/popular.dta, clear
gllamm popular, i(school) adapt
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 5.8576802
gllamm model
log likelihood = -2556.3612
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | 5.307604 .0950217 55.86 0.000 5.121365 5.493843
------------------------------------------------------------------------------
Variance at level 1
-----------------------------------------------------------------------------
.63867681 (.02072164)
Variances and covariances of random effects
-----------------------------------------------------------------------------
***level 2 (school)
var(1): .87068762 (.12771943)
-----------------------------------------------------------------------------
di 2*2556.3612
5112.7224
Part 2: The variable sex is included as a fixed effect. This has been done in table 4.1.
gen cons = 1
eq sch_c: cons
gllamm popular sex, i(school) adapt nrf(1) eq(sch_c )
Iteration 0: log likelihood = -2242.4431 (not concave)
Iteration 1: log likelihood = -2242.4431
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 5.8538169
gllamm model
log likelihood = -2242.4431
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sex | .8437617 .0309587 27.25 0.000 .7830838 .9044396
_cons | 4.897324 .0948272 51.64 0.000 4.711466 5.083182
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.45976423 (.01491828)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .85332444 (.12397587)
------------------------------------------------------------------------------
Part 3: The variable texp is also included.
gllamm popular sex texp, i(school) adapt nrf(1) eq(sch_c )
Iteration 0: log likelihood = -2214.2878
Iteration 1: log likelihood = -2214.2878 (backed up)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 37.965306
gllamm model
log likelihood = -2214.2878
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sex | .844684 .030945 27.30 0.000 .784033 .9053351
texp | .093589 .0107724 8.69 0.000 .0724755 .1147026
_cons | 3.558824 .1701959 20.91 0.000 3.225246 3.892402
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.45972135 (.01491621)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .47832207 (.07123085)
------------------------------------------------------------------------------
Part 4: The variable sex is included as a random effect.
gllamm popular sex texp, i(school) adapt nrf(2) eq(sch_c sch_s)
Iteration 0: log likelihood = -2130.5924
Iteration 1: log likelihood = -2130.5924 (backed up)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 40.750775
gllamm model
log likelihood = -2130.5924
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sex | .8432268 .0596367 14.14 0.000 .726341 .9601127
texp | .1086393 .0109591 9.91 0.000 .0871599 .1301187
_cons | 3.335057 .1703027 19.58 0.000 3.00127 3.668844
------------------------------------------------------------------------------
Variance at level 1
------------------------------------------------------------------------------
.39215591 (.01307054)
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (school)
var(1): .40612555 (.06376658)
cov(2,1): .02252195 (.0433015) cor(2,1): .06767289
var(2): .27272335 (.05087203)
------------------------------------------------------------------------------
Part 5: The interaction of sex and texp is included. This is Part 2 of table 4.2.
gen gxt = sex*texp
gllamm popular texp sex gxt, i(school) adapt nrf(2) eq(sch_c sch_s)
number of level 1 units = 2000
number of level 2 units = 100
Condition Number = 45.72526
gllamm model
log likelihood = -2122.9085
------------------------------------------------------------------------------
popular | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
texp | .1102169 .0099904 11.03 0.000 .090636 .1297977
sex | 1.32949 .130912 10.16 0.000 1.072907 1.586073
gxt | -.034026 .0083388 -4.08 0.000 -.0503697 -.0176822
_cons | 3.313841 .1566164 21.16 0.000 3.006879 3.620804
------------------------------------------------------------------------------
Variance at level 1
-----------------------------------------------------------------------------
.39236316 (.01308622)
Variances and covariances of random effects
-----------------------------------------------------------------------------
***level 2 (school)
var(1): .40543808 (.0627154)
cov(1,2): .02386608 (.03657119) cor(1,2): .0795611
var(2): .22194032 (.04304873)
-----------------------------------------------------------------------------
Table 4.4 can be produced manually based on the equations provided in this section. We omit the calculation here.