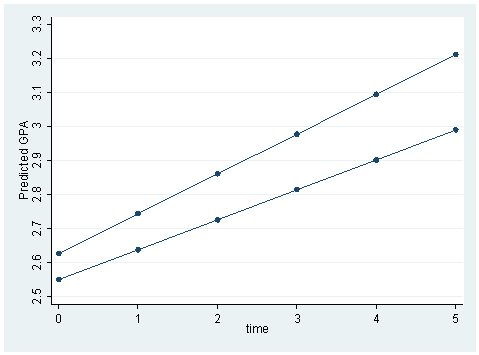Note: the following analysis and results were performed with Stata 14.2
This chapter uses data file gpach5.dta and vocagrwt.dta.
Table 5.1 on page 78.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/gpach5, clear keep student sex highgpa gpa time reshape wide gpa, i(student) j(time) mat ymat=(1,0,0,0,0,-1\0,1,0,0,0,-1\0,0,1,0,0,-1\0,0,0,1,0,-1\0,0,0,0,1,-1) manova gpa0 gpa1 gpa2 gpa3 gpa4 gpa5 = sex c.highgpa Number of obs = 200 W = Wilks' lambda L = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+------------------------------------------------------- Model |W 0.8506 2 12.0 384.0 2.70 0.0017 e |P 0.1534 12.0 386.0 2.67 0.0018 a |L 0.1708 12.0 382.0 2.72 0.0015 a |R 0.1360 6.0 193.0 4.37 0.0004 u |------------------------------------------------------- Residual | 197 -----------+------------------------------------------------------- sex |W 0.9049 1 6.0 192.0 3.36 0.0036 e |P 0.0951 6.0 192.0 3.36 0.0036 e |L 0.1051 6.0 192.0 3.36 0.0036 e |R 0.1051 6.0 192.0 3.36 0.0036 e |------------------------------------------------------- highgpa |W 0.9323 1 6.0 192.0 2.33 0.0343 e |P 0.0677 6.0 192.0 2.33 0.0343 e |L 0.0727 6.0 192.0 2.33 0.0343 e |R 0.0727 6.0 192.0 2.33 0.0343 e |------------------------------------------------------- Residual | 197 -----------+------------------------------------------------------- Total | 199 ------------------------------------------------------------------- e = exact, a = approximate, u = upper bound on F *GPA as categorical mat xcat = (0.5, 0.5,0,1) manovatest, test(xcat) ytransform(ymat) Transformations of the dependent variables (1) gpa0 - gpa5 (2) gpa1 - gpa5 (3) gpa2 - gpa5 (4) gpa3 - gpa5 (5) gpa4 - gpa5 Test constraint (1) .5*0.sex + .5*1.sex + _cons = 0 W = Wilks' lambda L = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+------------------------------------------------------- manovatest |W 0.8950 1 5.0 193.0 4.53 0.0006 e |P 0.1050 5.0 193.0 4.53 0.0006 e |L 0.1173 5.0 193.0 4.53 0.0006 e |R 0.1173 5.0 193.0 4.53 0.0006 e |------------------------------------------------------- Residual | 197 ------------------------------------------------------------------- e = exact, a = approximate, u = upper bound on F *linear trend mat ylin =(-5,-3,-1,1,3,5) manovatest, test(xcat) ytransform(ylin) Transformation of the dependent variables (1) -5*gpa0 - 3*gpa1 - gpa2 + gpa3 + 3*gpa4 + 5*gpa5 Test constraint (1) .5*0.sex + .5*1.sex + _cons = 0 W = Wilks' lambda L = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+------------------------------------------------------- manovatest |W 0.9391 1 1.0 197.0 12.77 0.0004 e |P 0.0609 1.0 197.0 12.77 0.0004 e |L 0.0648 1.0 197.0 12.77 0.0004 e |R 0.0648 1.0 197.0 12.77 0.0004 e |------------------------------------------------------- Residual | 197 ------------------------------------------------------------------- e = exact, a = approximate, u = upper bound on F *gpa*highgpa manovatest c.highgpa, ytransform(ymat) Transformations of the dependent variables (1) gpa0 - gpa5 (2) gpa1 - gpa5 (3) gpa2 - gpa5 (4) gpa3 - gpa5 (5) gpa4 - gpa5 W = Wilks' lambda L = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+------------------------------------------------------- highgpa |W 0.9781 1 5.0 193.0 0.87 0.5053 e |P 0.0219 5.0 193.0 0.87 0.5053 e |L 0.0224 5.0 193.0 0.87 0.5053 e |R 0.0224 5.0 193.0 0.87 0.5053 e |------------------------------------------------------- Residual | 197 ------------------------------------------------------------------- e = exact, a = approximate, u = upper bound on F
*gpa*gender mat xsex = (1, -1, 0) manovatest, test(xsex) ytransform(ymat) Transformations of the dependent variables (1) gpa0 - gpa5 (2) gpa1 - gpa5 (3) gpa2 - gpa5 (4) gpa3 - gpa5 (5) gpa4 - gpa5 Test constraint (1) 0.sex - 1.sex = 0 W = Wilks' lambda L = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+------------------------------------------------------- manovatest |W 0.9646 1 5.0 193.0 1.42 0.2196 e |P 0.0354 5.0 193.0 1.42 0.2196 e |L 0.0367 5.0 193.0 1.42 0.2196 e |R 0.0367 5.0 193.0 1.42 0.2196 e |------------------------------------------------------- Residual | 197 ------------------------------------------------------------------- e = exact, a = approximate, u = upper bound on F *test highgpa mat ym = 1/6*(1,1,1,1,1,1) manovatest c.highgpa, ytransform(ym) Transformation of the dependent variables (1) .1666667*gpa0 + .1666667*gpa1 + .1666667*gpa2 + .1666667*gpa3 + .1666667*gpa4 + .1666667*gpa5 W = Wilks' lambda L = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+------------------------------------------------------- highgpa |W 0.9556 1 1.0 197.0 9.16 0.0028 e |P 0.0444 1.0 197.0 9.16 0.0028 e |L 0.0465 1.0 197.0 9.16 0.0028 e |R 0.0465 1.0 197.0 9.16 0.0028 e |------------------------------------------------------- Residual | 197 ------------------------------------------------------------------- e = exact, a = approximate, u = upper bound on F *test sex manovatest, test(xsex) ytransform(ym) Transformation of the dependent variables (1) .1666667*gpa0 + .1666667*gpa1 + .1666667*gpa2 + .1666667*gpa3 + .1666667*gpa4 + .1666667*gpa5 Test constraint (1) 0.sex - 1.sex = 0 W = Wilks' lambda L = Lawley-Hotelling trace P = Pillai's trace R = Roy's largest root Source | Statistic df F(df1, df2) = F Prob>F -----------+------------------------------------------------------- manovatest |W 0.9147 1 1.0 197.0 18.37 0.0000 e |P 0.0853 1.0 197.0 18.37 0.0000 e |L 0.0933 1.0 197.0 18.37 0.0000 e |R 0.0933 1.0 197.0 18.37 0.0000 e |------------------------------------------------------- Residual | 197 ------------------------------------------------------------------- e = exact, a = approximate, u = upper bound on F
Table 5.2 on page 79.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/gpach5, clear collapse (mean) gpa, by(time sex) table sex time, contents(mean gpa) col row format(%3.1f)
----------------------------------------------------------- | time sex | 0 1 2 3 4 5 Total ----------+------------------------------------------------ 0 | 2.6 2.7 2.7 2.8 2.9 3.0 2.8 1 | 2.6 2.8 2.9 3.0 3.1 3.2 2.9 | Total | 2.6 2.7 2.8 2.9 3.0 3.1 2.9 -----------------------------------------------------------
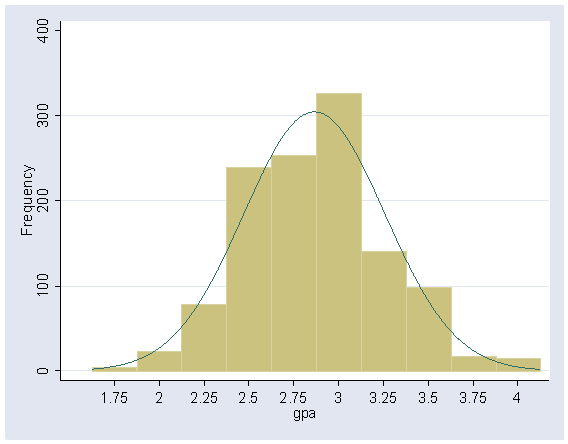
Figure 5.3 on page 80.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/gpach5, clear histogram gpa, normal frequency width(.25) start(1.625) xlabel(1.75(.25)4)
Table 5.3 on page 81.
Part 1: Null model.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/gpach5, clear
mixed gpa ||student:, var ml
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -456.72811
Iteration 1: log likelihood = -456.72811
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(0) = .
Log likelihood = -456.72811 Prob > chi2 = .
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | 2.865 .0191093 149.93 0.000 2.827546 2.902454
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Identity |
var(_cons) | .0567683 .0073395 .0440612 .0731402
-----------------------------+------------------------------------------------
var(Residual) | .09759 .0043644 .0894002 .1065301
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 249.82 Prob >= chibar2 = 0.0000
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 1,200 . -456.7281 3 919.4562 934.7265
-----------------------------------------------------------------------------
Part 2: With additional variable time.
mixed gpa time ||student:, var ml
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -196.82458
Iteration 1: log likelihood = -196.82458
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(1) = 681.70
Log likelihood = -196.82458 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .1063143 .0040719 26.11 0.000 .0983336 .114295
_cons | 2.599214 .0216516 120.05 0.000 2.556778 2.641651
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Identity |
var(_cons) | .0633616 .0073161 .050529 .0794532
-----------------------------+------------------------------------------------
var(Residual) | .0580305 .0025952 .0531605 .0633465
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 481.33 Prob >= chibar2 = 0.0000
estat ic
------------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+----------------------------------------------------------------
. | 1200 . -196.8246 4 401.6492 422.0095
------------------------------------------------------------------------------
Part 3: The variable job is added.
mixed gpa time job ||student:, var ml
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -160.1304
Iteration 1: log likelihood = -160.1304
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(2) = 788.20
Log likelihood = -160.1304 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .103166 .0040021 25.78 0.000 .0953219 .11101
job | -.1608636 .018356 -8.76 0.000 -.1968408 -.1248864
_cons | 2.945837 .044462 66.26 0.000 2.858693 3.032981
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Identity |
var(_cons) | .0533597 .0063712 .0422258 .0674291
-----------------------------+------------------------------------------------
var(Residual) | .0556077 .002494 .0509282 .0607171
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 388.27 Prob >= chibar2 = 0.0000
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 1,200 . -160.1304 5 330.2608 355.7112
-----------------------------------------------------------------------------
Note: N=Obs used in calculating BIC; see [R] BIC note.
Part 4: The variable highgpa and sex are added to the model.
mixed gpa time job highgpa sex ||student:, var ml
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -147.27246
Iteration 1: log likelihood = -147.27246
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(4) = 820.13
Log likelihood = -147.27246 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .1031482 .0040024 25.77 0.000 .0953037 .1109926
job | -.1617732 .0183036 -8.84 0.000 -.1976476 -.1258988
highgpa | .0858379 .0279769 3.07 0.002 .0310042 .1406717
sex | .1483967 .0333128 4.45 0.000 .0831048 .2136886
_cons | 2.613448 .0982039 26.61 0.000 2.420972 2.805924
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Identity |
var(_cons) | .0457555 .0056063 .0359872 .0581754
-----------------------------+------------------------------------------------
var(Residual) | .055617 .0024948 .0509361 .0607281
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 333.27 Prob >= chibar2 = 0.0000
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 1,200 . -147.2725 7 308.5449 344.1755
-----------------------------------------------------------------------------
Note: N=Obs used in calculating BIC; see [R] BIC note.
Table 5.4 on page 83.
Part 1: The variable time is included as a random effect.
mixed gpa time job highgpa sex ||student: time, var ml cov(un)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -90.102483
Iteration 1: log likelihood = -90.102468
Iteration 2: log likelihood = -90.102468
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(4) = 431.48
Log likelihood = -90.102468 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .1039731 .0056223 18.49 0.000 .0929537 .1149925
job | -.1196211 .0174584 -6.85 0.000 -.1538388 -.0854033
highgpa | .0898354 .0264746 3.39 0.001 .0379462 .1417246
sex | .1167606 .0315324 3.70 0.000 .0549583 .178563
_cons | 2.527287 .0926005 27.29 0.000 2.345793 2.70878
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Unstructured |
var(time) | .0039121 .0006455 .002831 .0054059
var(_cons) | .0389692 .0062212 .0284991 .0532858
cov(time,_cons) | -.0025635 .0015582 -.0056175 .0004905
-----------------------------+------------------------------------------------
var(Residual) | .0417646 .0020993 .0378462 .0460887
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 447.61 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 1,200 . -90.10247 9 198.2049 244.0156
-----------------------------------------------------------------------------
Note: N=Obs used in calculating BIC; see [R] BIC note.
Part 2: Cross level interaction of variable time and sex is included. We first created the interaction term.
gen sxtime= sex*time
mixed gpa time job highgpa sex sxtime ||student: time, var ml cov(un)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -86.602037
Iteration 1: log likelihood = -86.602002
Iteration 2: log likelihood = -86.602002
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(5) = 452.34
Log likelihood = -86.602002 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .0884798 .0080081 11.05 0.000 .0727841 .1041754
job | -.1206129 .0174249 -6.92 0.000 -.1547651 -.0864606
highgpa | .0898068 .0264668 3.39 0.001 .0379327 .1416808
sex | .0767958 .0348988 2.20 0.028 .0083954 .1451962
sxtime | .0294742 .0110399 2.67 0.008 .0078363 .051112
_cons | 2.550491 .0928935 27.46 0.000 2.368423 2.732559
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Unstructured |
var(time) | .0036912 .0006242 .0026499 .0051418
var(_cons) | .0385556 .0061494 .0282049 .0527048
cov(time,_cons) | -.002273 .0015061 -.0052248 .0006789
-----------------------------+------------------------------------------------
var(Residual) | .0417767 .0021004 .0378562 .0461031
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 446.52 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference
estat ic
------------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+----------------------------------------------------------------
. | 1200 . -86.602 10 193.204 244.1048
------------------------------------------------------------------------------
Figure 5.4 on page 84 based on the previous model.
gen p = 2.55 + .088*time + .0768*sex + .029*sxtime sort sex time label variable p "Predicted GPA" twoway scatter p time, connect(L) ylabel(2.5(.1)3.3)
Table 5.5 on page 85.
tab time
time | Freq. Percent Cum.
------------+-----------------------------------
0 | 200 16.67 16.67
1 | 200 16.67 33.33
2 | 200 16.67 50.00
3 | 200 16.67 66.67
4 | 200 16.67 83.33
5 | 200 16.67 100.00
------------+-----------------------------------
Total | 1,200 100.00
Part 1: 1st occasion = 0, same as the first part of Table 5.4.
mixed gpa time job highgpa sex ||student: time, var ml cov(un)
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .1039731 .0056223 18.49 0.000 .0929537 .1149925
job | -.1196211 .0174584 -6.85 0.000 -.1538388 -.0854033
highgpa | .0898354 .0264746 3.39 0.001 .0379462 .1417246
sex | .1167606 .0315324 3.70 0.000 .0549583 .178563
_cons | 2.527287 .0926005 27.29 0.000 2.345793 2.70878
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Unstructured |
var(time) | .0039121 .0006455 .002831 .0054059
var(_cons) | .0389692 .0062212 .0284991 .0532858
cov(time,_cons) | -.0025635 .0015582 -.0056175 .0004905
-----------------------------+------------------------------------------------
var(Residual) | .0417646 .0020993 .0378462 .0460887
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 447.61 Prob > chi2 = 0.0000
Part 2: The variable time has been recoded as -5, …,-1, 0, …with the last occasion coded as zero. We first recode variable time into time1.
gen time1 = time -5 mixed gpa time1 job highgpa sex ||student: time1, var ml cov(un)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -90.102485
Iteration 1: log likelihood = -90.102468
Iteration 2: log likelihood = -90.102468
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(4) = 431.48
Log likelihood = -90.102468 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time1 | .1039731 .0056223 18.49 0.000 .0929537 .1149926
job | -.1196211 .0174584 -6.85 0.000 -.1538388 -.0854033
highgpa | .0898354 .0264746 3.39 0.001 .0379462 .1417246
sex | .1167606 .0315324 3.70 0.000 .0549583 .178563
_cons | 3.047152 .0938291 32.48 0.000 2.86325 3.231054
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Unstructured |
var(time1) | .0039121 .0006455 .002831 .0054059
var(_cons) | .1111359 .0137347 .0872286 .1415956
cov(time1,_cons) | .0169968 .002676 .0117519 .0222417
-----------------------------+------------------------------------------------
var(Residual) | .0417646 .0020993 .0378462 .0460887
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 447.61 Prob > chi2 = 0.0000
Part 3: The variable time is recoded centered around its mean and is included as a fixed effect.
gen timec = time - 2.5
mixed gpa timec job highgpa sex ||student: timec, var ml cov(un)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -90.102706
Iteration 1: log likelihood = -90.102468
Iteration 2: log likelihood = -90.102468
Computing standard errors:
Mixed-effects ML regression Number of obs = 1200
Group variable: student Number of groups = 200
Obs per group: min = 6
avg = 6.0
max = 6
Wald chi2(4) = 431.48
Log likelihood = -90.102468 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
timec | .1039731 .0056223 18.49 0.000 .0929537 .1149926
job | -.1196211 .0174584 -6.85 0.000 -.1538388 -.0854033
highgpa | .0898354 .0264746 3.39 0.001 .0379462 .1417246
sex | .1167606 .0315324 3.70 0.000 .0549583 .178563
_cons | 2.787219 .092151 30.25 0.000 2.606607 2.967832
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Unstructured |
var(timec) | .0039121 .0006455 .002831 .0054059
var(_cons) | .0506022 .0058846 .0402885 .063556
cov(timec,_cons) | .0072167 .0014799 .0043162 .0101172
-----------------------------+------------------------------------------------
var(Residual) | .0417646 .0020993 .0378462 .0460887
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 447.61 Prob > chi2 = 0.0000
Table 5.6 using data file vocagrwt.dta.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/vocagrwt, clear
table age, contents (count child)
----------------------
age in |
months | N(child)
----------+-----------
12 | 22
14 | 5
16 | 22
18 | 11
20 | 22
22 | 11
24 | 22
26 | 11
----------------------
Table 5.7 on page 89. We have to recode the variable study as follows.
Part 1: Intercept only model.
gen study1 = study - .5
mixed vocab study1 ||child:, var ml cov(un)
Note: single-variable random-effects specification; covariance structure set to
identity
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -834.45287
Iteration 1: log likelihood = -834.45002
Iteration 2: log likelihood = -834.45001
Computing standard errors:
Mixed-effects ML regression Number of obs = 126
Group variable: child Number of groups = 22
Obs per group: min = 4
avg = 5.7
max = 8
Wald chi2(1) = 8.08
Log likelihood = -834.45001 Prob > chi2 = 0.0045
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -110.912 39.0169 -2.84 0.004 -187.3838 -34.44031
_cons | 132.0697 19.50845 6.77 0.000 93.83379 170.3055
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Identity |
var(_cons) | 2400.597 2148.08 415.5804 13867.03
-----------------------------+------------------------------------------------
var(Residual) | 31075.49 4201.565 23841.37 40504.64
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 1.94 Prob >= chibar2 = 0.0821
Part 2: The variable age is grand mean centered and is included as a fixed effect.
sum age
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
age | 126 18.88889 4.578598 12 26
gen agec=age-r(mean)
mixed vocab study1 agec ||child:, var ml cov(un)
Note: single-variable random-effects specification; covariance structure set to
identity
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -775.46764
Iteration 1: log likelihood = -775.46764
Computing standard errors:
Mixed-effects ML regression Number of obs = 126
Group variable: child Number of groups = 22
Obs per group: min = 4
avg = 5.7
max = 8
Wald chi2(2) = 225.19
Log likelihood = -775.46764 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -69.79256 35.47381 -1.97 0.049 -139.3199 -.2651797
agec | 29.55533 2.013816 14.68 0.000 25.60832 33.50233
_cons | 137.7813 17.68648 7.79 0.000 103.1165 172.4462
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Identity |
var(_cons) | 4882.778 1937.101 2243.765 10625.68
-----------------------------+------------------------------------------------
var(Residual) | 10377.41 1421.189 7934.449 13572.54
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 26.44 Prob >= chibar2 = 0.0000
Part 3: The squared term of agec is included as a fixed effect.
gen agec2 = agec*agec
mixed vocab study1 agec agec2 ||child:, var ml cov(un)
Note: single-variable random-effects specification; covariance structure set to
identity
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -759.74092
Iteration 1: log likelihood = -759.74092
Computing standard errors:
Mixed-effects ML regression Number of obs = 126
Group variable: child Number of groups = 22
Obs per group: min = 4
avg = 5.7
max = 8
Wald chi2(3) = 336.38
Log likelihood = -759.74092 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -68.25089 34.85923 -1.96 0.050 -136.5737 .0719371
agec | 30.62189 1.746006 17.54 0.000 27.19978 34.04399
agec2 | 2.557313 .422708 6.05 0.000 1.728821 3.385806
_cons | 84.79167 19.46981 4.36 0.000 46.63154 122.9518
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Identity |
var(_cons) | 5166.262 1902.714 2510.049 10633.36
-----------------------------+------------------------------------------------
var(Residual) | 7721.242 1060.154 5899.485 10105.55
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 38.85 Prob >= chibar2 = 0.0000
Part 4: The centered variable agec is included as a random effect.
mixed vocab study1 agec agec2 || child: agec, var ml cov(un)
(note Stata 14.2 results in Hessian not negative semidefinite error)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -651.93737
Iteration 1: log likelihood = -651.40036
Iteration 2: log likelihood = -651.37911
Iteration 3: log likelihood = -651.37642
Iteration 4: log likelihood = -651.37628
Iteration 5: log likelihood = -651.37626
Computing standard errors:
Mixed-effects ML regression Number of obs = 126
Group variable: child Number of groups = 22
Obs per group: min = 4
avg = 5.7
max = 8
Wald chi2(3) = 288.74
Log likelihood = -651.37626 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -4.971305 8.003023 -0.62 0.534 -20.65694 10.71433
agec | 28.13162 3.399128 8.28 0.000 21.46945 34.79379
agec2 | 2.175139 .1454073 14.96 0.000 1.890146 2.460132
_cons | 87.982 17.52353 5.02 0.000 53.63651 122.3275
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Unstructured |
var(agec) | 245.7646 76.12805 133.9218 451.0114
var(_cons) | 6399.886 1995.074 3473.939 11790.23
cov(agec,_cons) | 1254.139 384.1707 501.1785 2007.1
-----------------------------+------------------------------------------------
var(Residual) | 862.6386 119.6392 657.3185 1132.092
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 255.58 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference
Table 5.8 on page 91.
Part 1: Intercept only model. This is Part 1 from Table 5.7. We only show the output here.
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -110.912 39.0169 -2.84 0.004 -187.3838 -34.44031
_cons | 132.0697 19.50845 6.77 0.000 93.83379 170.3055
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Identity |
var(_cons) | 2400.597 2148.08 415.5804 13867.03
-----------------------------+------------------------------------------------
var(Residual) | 31075.49 4201.565 23841.37 40504.64
------------------------------------------------------------------------------
Part 2: The variable age is centered on 12 months and is included as a fixed effect.
mixed vocab study1 age12 ||child: , var ml cov(un)
Note: single-variable random-effects specification; covariance structure set to
identity
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -775.46764
Iteration 1: log likelihood = -775.46764
Computing standard errors:
Mixed-effects ML regression Number of obs = 126
Group variable: child Number of groups = 22
Obs per group: min = 4
avg = 5.7
max = 8
Wald chi2(2) = 225.19
Log likelihood = -775.46764 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -69.79256 35.47381 -1.97 0.049 -139.3199 -.2651795
age12 | 29.55533 2.013816 14.68 0.000 25.60832 33.50233
_cons | -65.82204 22.2324 -2.96 0.003 -109.3967 -22.24734
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Identity |
var(_cons) | 4882.778 1937.101 2243.765 10625.68
-----------------------------+------------------------------------------------
var(Residual) | 10377.41 1421.189 7934.449 13572.54
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 26.44 Prob >= chibar2 = 0.0000
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 126 . -775.4676 5 1560.935 1575.117
-----------------------------------------------------------------------------
Note: N=Obs used in calculating BIC; see [R] BIC note.
Part 3: The variable age12sq is included as a fixed effect.
mixed vocab study1 age12 age12sq ||child: , var ml cov(un)
Note: single-variable random-effects specification; covariance structure set to
identity
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -759.74092
Iteration 1: log likelihood = -759.74092
Computing standard errors:
Mixed-effects ML regression Number of obs = 126
Group variable: child Number of groups = 22
Obs per group:
min = 4
avg = 5.7
max = 8
Wald chi2(3) = 336.38
Log likelihood = -759.74092 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -68.25089 34.85924 -1.96 0.050 -136.5737 .0719587
age12 | -4.612211 5.910617 -0.78 0.435 -16.19681 6.972385
age12sq | 2.557313 .422708 6.05 0.000 1.728821 3.385806
_cons | -4.797205 23.22993 -0.21 0.836 -50.32703 40.73262
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Identity |
var(_cons) | 5166.266 1902.716 2510.051 10633.37
-----------------------------+------------------------------------------------
var(Residual) | 7721.241 1060.154 5899.485 10105.55
------------------------------------------------------------------------------
LR test vs. linear model: chibar2(01) = 38.85 Prob >= chibar2 = 0.0000
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 126 . -759.7409 6 1531.482 1548.5
-----------------------------------------------------------------------------
Note: N=Obs used in calculating BIC; see [R] BIC note.
Part 4: The variable age12 is a random effect.
mixed vocab study1 age12 age12sq ||child: age12, var ml cov(un)
(note Stata 14.2 results in Hessian not negative semidefinite error)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -652.0315
Iteration 1: log likelihood = -651.50087
Iteration 2: log likelihood = -651.40437
Iteration 3: log likelihood = -651.38281
Iteration 4: log likelihood = -651.37783
Iteration 5: log likelihood = -651.37663
Iteration 6: log likelihood = -651.37632
Iteration 7: log likelihood = -651.37627
Iteration 8: log likelihood = -651.37626
Computing standard errors:
Mixed-effects ML regression Number of obs = 126
Group variable: child Number of groups = 22
Obs per group: min = 4
avg = 5.7
max = 8
Wald chi2(3) = 288.73
Log likelihood = -651.37626 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
vocab | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
study1 | -4.975021 8.002868 -0.62 0.534 -20.66035 10.71031
age12 | -1.836976 3.891349 -0.47 0.637 -9.46388 5.789927
age12sq | 2.17514 .1454086 14.96 0.000 1.890144 2.460136
_cons | -2.588417 8.341687 -0.31 0.756 -18.93782 13.76099
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
child: Unstructured |
var(age12) | 245.7569 76.12895 133.9141 451.0091
var(_cons) | 784.0285 361.7215 317.409 1936.62
cov(age12,_cons) | -438.9538 159.5462 -751.6586 -126.2489
-----------------------------+------------------------------------------------
var(Residual) | 862.6541 119.6425 657.3286 1132.116
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 255.58 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 126 . -779.1681 4 1566.336 1577.681
-----------------------------------------------------------------------------
Note: N=Obs used in calculating BIC; see [R] BIC note.
Table 5.9 on page 92 is created using HLM. We omit it here.
Table 5.10 on page 101 using the data file gpach5.dta.
use https://stats.idre.ucla.edu/stat/stata/examples/mlm_ma_hox/gpach5, clear
Part 1: The variable time is a fixed effect. We have built the model at the beginning of this chapter. We will use it here.
mixed gpa time job highgpa sex ||student: , var ml
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .1031482 .0040024 25.77 0.000 .0953037 .1109926
job | -.1617732 .0183036 -8.84 0.000 -.1976476 -.1258988
highgpa | .0858379 .0279769 3.07 0.002 .0310042 .1406717
sex | .1483967 .0333128 4.45 0.000 .0831048 .2136886
_cons | 2.613448 .0982039 26.61 0.000 2.420972 2.805924
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Identity |
var(_cons) | .0457555 .0056063 .0359872 .0581754
-----------------------------+------------------------------------------------
var(Residual) | .055617 .0024948 .0509361 .0607281
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 333.27 Prob >= chibar2 = 0.0000
Part 2: The variable time is included as random effect. This is Part 1 of table 5.4.
mixed gpa time job highgpa sex ||student: time, var ml cov(un)
------------------------------------------------------------------------------
gpa | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time | .1039731 .0056223 18.49 0.000 .0929537 .1149925
job | -.1196211 .0174584 -6.85 0.000 -.1538388 -.0854033
highgpa | .0898354 .0264746 3.39 0.001 .0379462 .1417246
sex | .1167606 .0315324 3.70 0.000 .0549583 .178563
_cons | 2.527287 .0926005 27.29 0.000 2.345793 2.70878
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
student: Unstructured |
var(time) | .0039121 .0006455 .002831 .0054059
var(_cons) | .0389692 .0062212 .0284991 .0532858
cov(time,_cons) | -.0025635 .0015582 -.0056175 .0004905
-----------------------------+------------------------------------------------
var(Residual) | .0417646 .0020993 .0378462 .0460887
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 447.61 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference
Part 3: The variable time is a fixed effect, MANOVA.