Table 14.2, page 369.
NOTE: The values shown in the text are listed as eigenvectors in the Stata output.
use https://stats.idre.ucla.edu/stat/stata/examples/pma5/depress, clear
pca c1-c20, factors(5)
Principal components/correlation Number of obs = 294
Number of comp. = 5
Trace = 20
Rotation: (unrotated = principal) Rho = 0.5925
--------------------------------------------------------------------------
Component | Eigenvalue Difference Proportion Cumulative
-------------+------------------------------------------------------------
Comp1 | 7.05542 5.56985 0.3528 0.3528
Comp2 | 1.48557 .25406 0.0743 0.4270
Comp3 | 1.23151 .165825 0.0616 0.4886
Comp4 | 1.06569 .0530524 0.0533 0.5419
Comp5 | 1.01263 .0451719 0.0506 0.5925
Comp6 | .967461 .0206444 0.0484 0.6409
Comp7 | .946816 .177579 0.0473 0.6883
Comp8 | .769238 .0746006 0.0385 0.7267
Comp9 | .694637 .0345101 0.0347 0.7614
Comp10 | .660127 .0524914 0.0330 0.7945
Comp11 | .607635 .0582981 0.0304 0.8248
Comp12 | .549337 .0127038 0.0275 0.8523
Comp13 | .536634 .027916 0.0268 0.8791
Comp14 | .508718 .057815 0.0254 0.9046
Comp15 | .450903 .0757216 0.0225 0.9271
Comp16 | .375181 .0539966 0.0188 0.9459
Comp17 | .321184 .0266216 0.0161 0.9619
Comp18 | .294563 .0261883 0.0147 0.9767
Comp19 | .268374 .0699963 0.0134 0.9901
Comp20 | .198378 . 0.0099 1.0000
--------------------------------------------------------------------------
Principal components (eigenvectors)
------------------------------------------------------------------------------
Variable | Comp1 Comp2 Comp3 Comp4 Comp5 | Unexplained
-------------+--------------------------------------------------+-------------
c1 | 0.2774 -0.1450 -0.0577 0.0027 -0.0883 | .4137
c2 | 0.3132 0.0271 -0.0316 -0.2478 -0.0244 | .2396
c3 | 0.2678 -0.1547 -0.0346 -0.2472 0.2183 | .3436
c4 | 0.2436 -0.3194 -0.1769 0.0716 0.1729 | .3556
c5 | 0.2868 -0.0497 -0.1384 -0.2794 0.0411 | .3076
c6 | 0.2206 0.0534 -0.2242 -0.1823 0.3399 | .4382
c7 | 0.2844 -0.1644 0.0190 0.0761 0.0870 | .3751
c8 | 0.1081 -0.3045 -0.1103 0.5567 0.0976 | .4249
c9 | 0.1758 -0.1690 0.3962 0.0146 -0.5355 | .2556
c10 | 0.2766 -0.0454 0.0835 -0.0084 -0.3651 | .3134
c11 | 0.2433 -0.1048 0.1314 -0.0414 -0.2419 | .4838
c12 | 0.1790 0.2300 -0.1634 -0.1451 -0.0368 | .6386
c13 | 0.1259 0.2126 -0.2645 0.5400 -0.0953 | .4148
c14 | 0.1803 0.4015 0.1014 0.2461 0.0847 | .4468
c15 | 0.2004 0.2098 -0.2703 -0.0312 -0.0834 | .5533
c16 | 0.1924 0.4174 0.1850 0.0467 0.0399 | .4338
c17 | 0.2097 0.3905 0.0860 0.0684 0.0499 | .4467
c18 | 0.1717 0.0153 -0.2019 0.0629 -0.2752 | .6605
c19 | 0.1315 0.0569 0.6326 0.0232 0.3349 | .2662
c20 | 0.2357 -0.2283 0.1933 0.2404 0.2909 | .3373
------------------------------------------------------------------------------
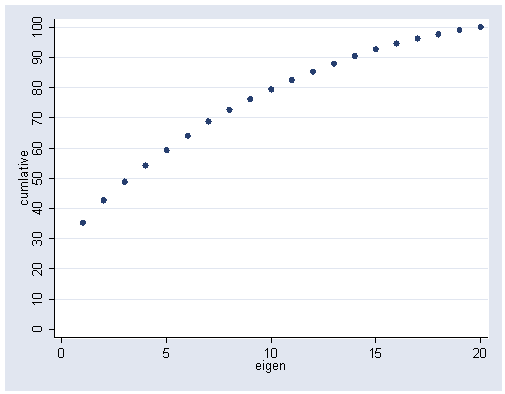
Figure 14.5, page 368.
Panel A:
matrix E1 = e(Ev) matrix E2 = E1' svmat E2, name(col) gen eigen = _n if r1 != . gen c = sum(r1) if r1 != . gen cumlative = (c/20)*100 graph twoway scatter cumlative eigen, ylabel(0(10)100)
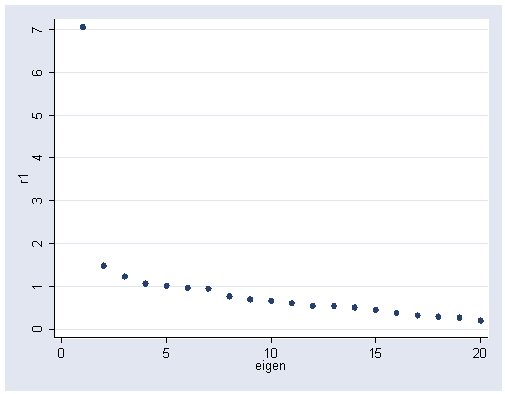
Panel B:
NOTE: The following graph can easily be reproduced using the greigen command, however, the greigen command only uses the first 13 eigenvalues.
graph twoway scatter r1 eigen, ylabel(0(1)7)