use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear (Hamilton (1983))
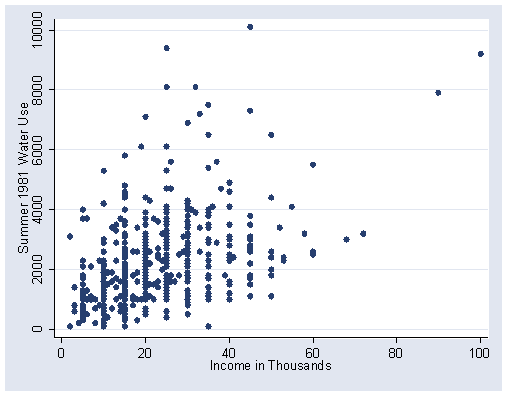
Figure 2.3, page 35.
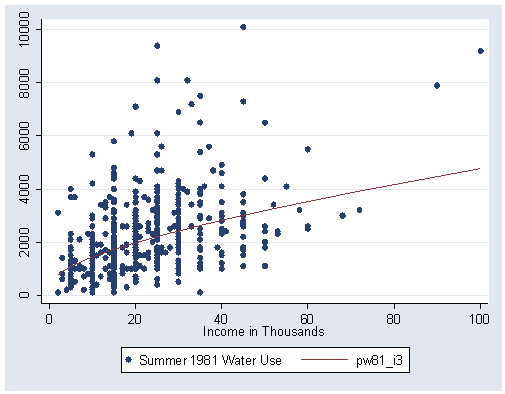
graph twoway scatter water81 income, xlabel(0(20)100) ylabel(0(2000)10000)
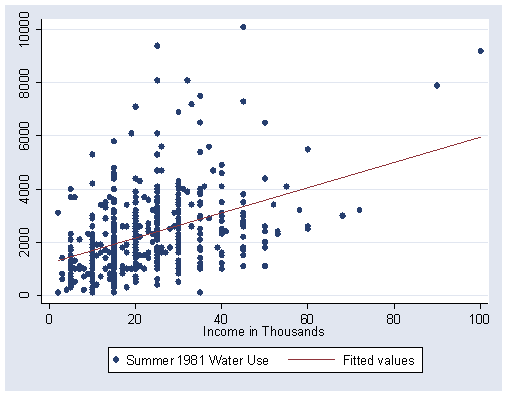
Figure 2.4, page 35.
graph twoway (scatter water81 income) (lfit water81 income), /// xlabel(0(20)100) ylabel(0(2000)10000)
Compute the regression of water81 using income as the predictor. The model estimates on page 36 are displayed. Note that the residual standard deviation is listed as the Root MSE in the output.
regress water81 income Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 1, 494) = 104.46 Model | 190820566 1 190820566 Prob > F = 0.0000 Residual | 902418143 494 1826757.38 R-squared = 0.1745 ---------+------------------------------ Adj R-squared = 0.1729 Total | 1.0932e+09 495 2208563.05 Root MSE = 1351.6 ------------------------------------------------------------------------------ water81 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- income | 47.54869 4.652286 10.221 0.000 38.40798 56.6894 _cons | 1201.124 123.3245 9.740 0.000 958.8191 1443.43 ------------------------------------------------------------------------------
Obtain the predicted values of water81, naming this variable pw81.
predict pw81 (option xb assumed; fitted values)
Obtain the residuals, naming this variable rw81.
predict rw81, resid
Use summarize to obtain the standard deviations of water81 and income on page 40. The regression coefficients and other regression estimates in this section were output previously using the regress command.
summarize income water81 Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- income | 496 23.07661 13.05784 2 100 water81 | 496 2298.387 1486.123 100 10100
The estimates and test statistics in this section were obtained previously with the regress command.
Figure 2.7, page 48. Graph the scatterplot with the 99% confidence and prediction bands. This graph was constructed by overlaying four separate graphs, a scatter plot (scatter water81 income), regression line (lfit water81 income), the confidence interval for the regression line (lfitci water81 income), and the prediction interval (lfitci water81 income, stdf ).
graph twoway (scatter water81 income) (lfit water81 income) ///
(lfitci water81 income, level(99) clcolor(blue) ciplot(rline)) ///
(lfitci water81 income, level(99) stdf ciplot(rline)), ///
xlabel(0 23 100) ylabel(0 10000, nogrid)
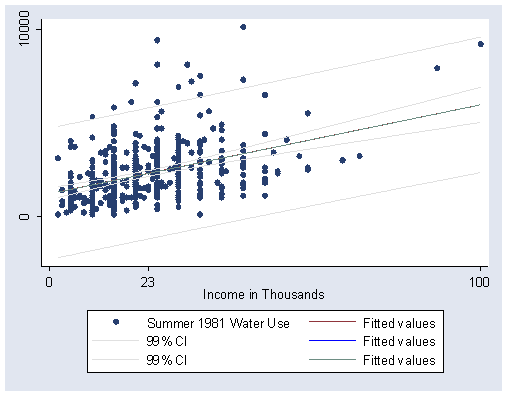
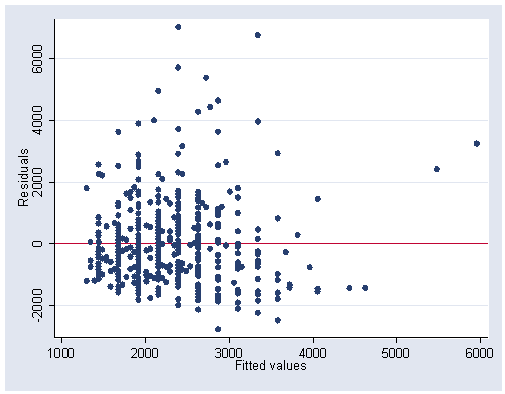
Figure 2.9, page 52.
rvfplot, yline(0) xlabel(1000(1000)6000) ylabel(-2000(2000)6000)
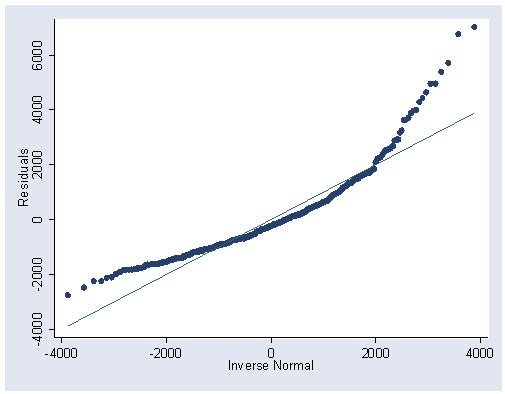
Figure 2.12, page 54.
qnorm rw81, xlab(-4000(2000)4000) ylab(-4000(2000)6000)
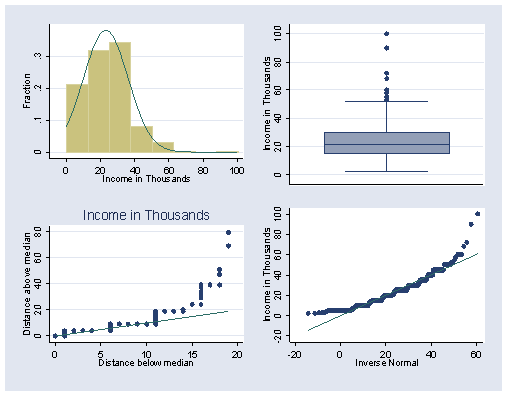
Figure 2.13, page 54. First graph and save the individual plots then graph them together.
histogram income, nodraw normal fraction bin(8) start(0) xlabel(0(20)100) ylabel(0(.1).3) saving(f2_13a,replace) graph box income, nodraw ylabel(0(20)100) saving(f2_13b,replace) symplot income, nodraw xlabel(0(5)20) ylabel(0(20)80) saving(f2_13c,replace) qnorm income, nodraw xlabel(-20(20)60) ylabel(-20(20)100) saving(f2_13d,replace) graph combine f2_13a.gph f2_13b.gph f2_13c.gph f2_13d.gph
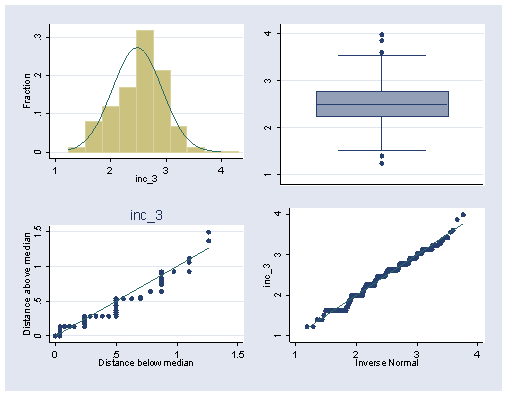
Figure 2.14, page 55. This is done the same way as figure 2.13 after we generate inc_3 which is income to the .3 power.
gen inc_3 = income^.3 histogram inc_3, nodraw fraction normal bin(9) xlabel(1(1)4) ylabel(0(.1).3) saving(f2_14a,replace) graph box inc_3, nodraw ylabel(1(1)4) saving(f2_14b,replace) symplot inc_3, nodraw xlabel(0(.5)1.5) ylabel(0(.5)1.5) saving(f2_14c,replace) qnorm inc_3, xlabel(1(1)4) ylabel(1(1)4) saving(f2_14d,replace)
graph combine f2_14a.gph f2_14b.gph f2_14c.gph f2_14d.gph
Table 2.3, page 55. Generate water81 to the .3 power and regress with the transformed income variable as a predictor.
gen wtr81_3 = water81^.3 regress wtr81_3 inc_3 Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 1, 494) = 126.22 Model | 370.337058 1 370.337058 Prob > F = 0.0000 Residual | 1449.41668 494 2.93404187 R-squared = 0.2035 ---------+------------------------------ Adj R-squared = 0.2019 Total | 1819.75374 495 3.67627019 Root MSE = 1.7129 ------------------------------------------------------------------------------ wtr81_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- inc_3 | 1.934535 .1721913 11.235 0.000 1.596217 2.272853 _cons | 4.989011 .4330577 11.520 0.000 4.138149 5.839873 ------------------------------------------------------------------------------
Compute the mean values in Table 2.3, page 55.
summ wtr81_3 inc_3 Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- wtr81_3 | 496 9.776982 1.91736 3.981072 15.89631 inc_3 | 496 2.474998 .4471152 1.231144 3.981072
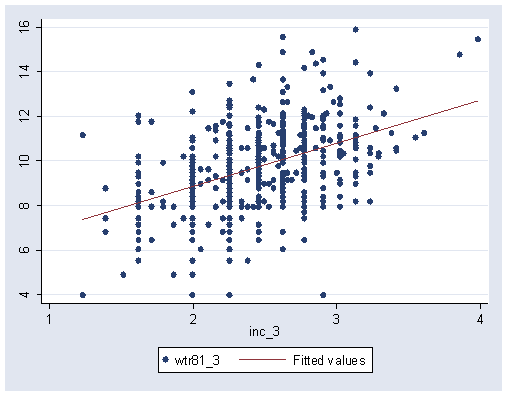
Figure 2.15, page 56.
graph twoway (scatter wtr81_3 inc_3) (lfit wtr81_3 inc_3), ylabel(4(2)16) xlabel(1(1)4)
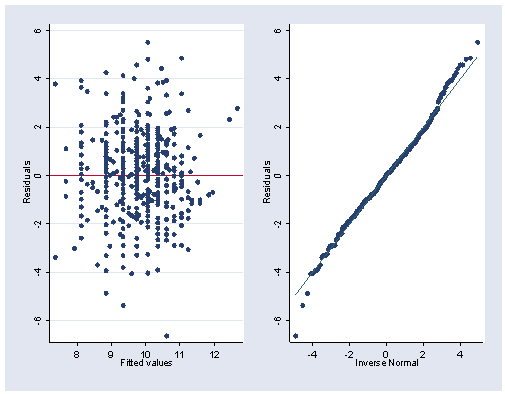
Figure 2.16, page 56. First obtain the predicted and residual values for the model with the transformed variables. Then graph and save the individual plots before graphing them together.
predict pw81_3 . predict rw81_3, resid . rvfplot, yline(0) xlab(8(1)12) ylab(-6(2)6) saving(f2_16a,replace) qnorm rw81_3, xlab(-4(2)4) ylabel(-6(2)6) saving(f2_16b,replace) graph combine f2_16a.gph f2_16b.gph
Figure 2.17, page 58. Generate pw81_i3, the inverse transformation of pw81_3 and graph it with income and water81. The sort option is needed to graph the curve properly.
gen pw81_i3 = pw81_3^(1/.3) graph twoway (scatter water81 income) (line pw81_i3 income, sort)
Save the changes we made to concord1 so that we can use another dataset without losing the changes we made. The new data is named concord1b.
save concord1b, replace use https://stats.idre.ucla.edu/stat/stata/examples/rwg/oilspill, clear (Accidental Oil Spills 1973-85)
Regress oil loss on the number of spills.
regress lost spills
Source | SS df MS Number of obs = 13
---------+------------------------------ F( 1, 11) = 6.03
Model | 167218.128 1 167218.128 Prob > F = 0.0319
Residual | 304843.616 11 27713.056 R-squared = 0.3542
---------+------------------------------ Adj R-squared = 0.2955
Total | 472061.744 12 39338.4787 Root MSE = 166.47
------------------------------------------------------------------------------
lost | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
spills | 6.956853 2.832131 2.456 0.032 .7233746 13.19033
_cons | -44.48731 102.6833 -0.433 0.673 -270.4918 181.5172
------------------------------------------------------------------------------
Regress oil loss on number of spills through the origin, using the noconstant option.
regress lost spills, noconstant
Source | SS df MS Number of obs = 13
---------+------------------------------ F( 1, 12) = 22.72
Model | 587004.77 1 587004.77 Prob > F = 0.0005
Residual | 310045.453 12 25837.1211 R-squared = 0.6544
---------+------------------------------ Adj R-squared = 0.6256
Total | 897050.223 13 69003.8633 Root MSE = 160.74
------------------------------------------------------------------------------
lost | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
spills | 5.860875 1.2296 4.766 0.000 3.181808 8.539943
------------------------------------------------------------------------------
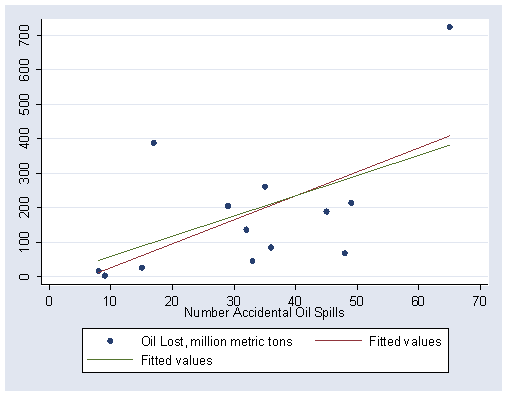
Figure 2.8, page 50.
graph twoway (scatter lost spills) (lfit lost spills) /// (lfit lost spills, estopts(noconstant)), /// ylabel(0(100)700) xlabel(0(10)70)
Save the changes made to a new dataset oilspill2.
save oilspill2