Table 3.1, page 68.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear (Hamilton (1983))
regress water81 income water80 Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 2, 493) = 391.76 Model | 671025350 2 335512675 Prob > F = 0.0000 Residual | 422213359 493 856416.551 R-squared = 0.6138 ---------+------------------------------ Adj R-squared = 0.6122 Total | 1.0932e+09 495 2208563.05 Root MSE = 925.43 ------------------------------------------------------------------------------ water81 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- income | 20.54504 3.38341 6.072 0.000 13.89736 27.19272 water80 | .5931267 .0250482 23.679 0.000 .5439123 .6423411 _cons | 203.8217 94.36129 2.160 0.031 18.42181 389.2216 ------------------------------------------------------------------------------
The means in table 3.1 are obtained separately using summarize.
summarize water81 income water80 Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- water81 | 496 2298.387 1486.123 100 10100 income | 496 23.07661 13.05784 2 100 water80 | 496 2732.056 1763.8 200 12700
Figure 3.1, page 70. First regress the partial model [3.10] and output the residuals using predict. We use the label command to label the residual variable.
regress water81 water80 predict ey_x2, resid label variable ey_x2 "e y|x2" Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 1, 494) = 696.11 Model | 639446987 1 639446987 Prob > F = 0.0000 Residual | 453791723 494 918606.727 R-squared = 0.5849 ---------+------------------------------ Adj R-squared = 0.5841 Total | 1.0932e+09 495 2208563.05 Root MSE = 958.44 ------------------------------------------------------------------------------ water81 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- water80 | .6443923 .0244238 26.384 0.000 .596405 .6923796 _cons | 537.871 79.40114 6.774 0.000 381.8654 693.8766 ------------------------------------------------------------------------------
Next regress partial model [3.11] then output and label the residual variable.
regress income water80 predict ex1_x2, resid label variable ex1_x2 "e x1|x2" Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 1, 494) = 63.31 Model | 9588.3167 1 9588.3167 Prob > F = 0.0000 Residual | 74812.772 494 151.442858 R-squared = 0.1136 ---------+------------------------------ Adj R-squared = 0.1118 Total | 84401.0887 495 170.50725 Root MSE = 12.306 ------------------------------------------------------------------------------ income | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- water80 | .0024953 .0003136 7.957 0.000 .0018791 .0031114 _cons | 16.25937 1.019498 15.948 0.000 14.25628 18.26245 ------------------------------------------------------------------------------
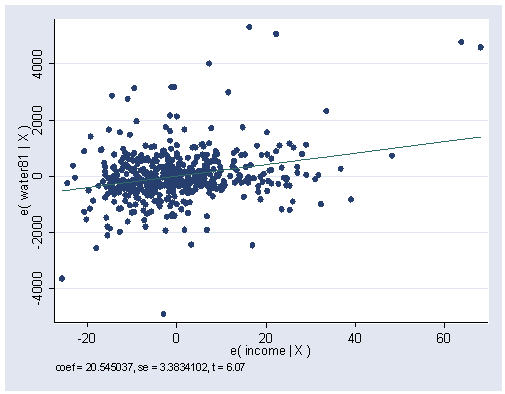
Figure 3.1, page 70. For the graph, we’ll run the full regression model and use the avplot command afterwards to get the plot.
quietly regress water81 income water80 avplot income, ylabel(-4000(2000)4000) xlabel(-20(20)60)
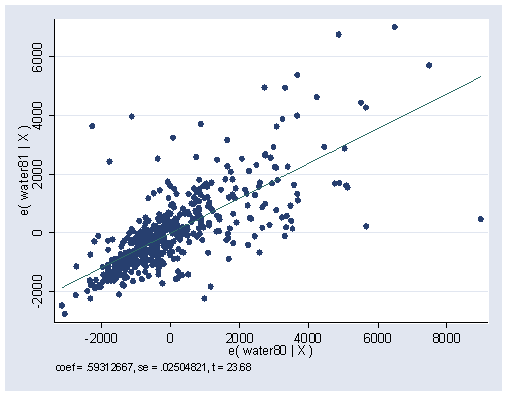
Figure 3.2, page 71.
avplot water80, ylabel(-2000(2000)6000) xlabel(-2000(2000)8000)
Table 3.2, page 74.
regress water81 income water80 educat retire peop81 cpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 6, 489) = 171.08 Model | 740477522 6 123412920 Prob > F = 0.0000 Residual | 352761188 489 721393.022 R-squared = 0.6773 ---------+------------------------------ Adj R-squared = 0.6734 Total | 1.0932e+09 495 2208563.05 Root MSE = 849.35 ------------------------------------------------------------------------------ water81 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- income | 20.96699 3.463719 6.053 0.000 14.16138 27.7726 water80 | .49194 .0263478 18.671 0.000 .440171 .5437089 educat | -41.86552 13.22031 -3.167 0.002 -67.84114 -15.8899 retire | 189.1843 95.02142 1.991 0.047 2.483674 375.885 peop81 | 248.197 28.7248 8.641 0.000 191.7578 304.6363 cpeop | 96.4536 80.51903 1.198 0.232 -61.75235 254.6596 _cons | 242.2204 206.8638 1.171 0.242 -164.2312 648.6721 ------------------------------------------------------------------------------ summ water81 income water80 educat retire peop81 cpeop Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- water81 | 496 2298.387 1486.123 100 10100 income | 496 23.07661 13.05784 2 100 water80 | 496 2732.056 1763.8 200 12700 educat | 496 14.00403 3.09055 6 20 retire | 496 .2943548 .4562123 0 1 peop81 | 496 3.072581 1.657177 1 10 cpeop | 496 -.0383065 .4846579 -3 3
Use the beta option to get the standardized regression coefficients.
regress water81 income water80 educat retire peop81 cpeop, beta Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 6, 489) = 171.08 Model | 740477522 6 123412920 Prob > F = 0.0000 Residual | 352761188 489 721393.022 R-squared = 0.6773 ---------+------------------------------ Adj R-squared = 0.6734 Total | 1.0932e+09 495 2208563.05 Root MSE = 849.35 ------------------------------------------------------------------------------ water81 | Coef. Std. Err. t P>|t| Beta ---------+-------------------------------------------------------------------- income | 20.96699 3.463719 6.053 0.000 .1842267 water80 | .49194 .0263478 18.671 0.000 .5838571 educat | -41.86552 13.22031 -3.167 0.002 -.0870637 retire | 189.1843 95.02142 1.991 0.047 .0580761 peop81 | 248.197 28.7248 8.641 0.000 .2767647 cpeop | 96.4536 80.51903 1.198 0.232 .0314557 _cons | 242.2204 206.8638 1.171 0.242 . ------------------------------------------------------------------------------
Use the level option to change the significance to 90%. The default is 95%.
regress water81 income water80 educat retire peop81 cpeop, level(90) Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 6, 489) = 171.08 Model | 740477522 6 123412920 Prob > F = 0.0000 Residual | 352761188 489 721393.022 R-squared = 0.6773 ---------+------------------------------ Adj R-squared = 0.6734 Total | 1.0932e+09 495 2208563.05 Root MSE = 849.35 ------------------------------------------------------------------------------ water81 | Coef. Std. Err. t P>|t| [90% Conf. Interval] ---------+-------------------------------------------------------------------- income | 20.96699 3.463719 6.053 0.000 15.25887 26.67512 water80 | .49194 .0263478 18.671 0.000 .4485193 .5353606 educat | -41.86552 13.22031 -3.167 0.002 -63.65226 -20.07877 retire | 189.1843 95.02142 1.991 0.047 32.59134 345.7773 peop81 | 248.197 28.7248 8.641 0.000 200.8592 295.5348 cpeop | 96.4536 80.51903 1.198 0.232 -36.23979 229.147 _cons | 242.2204 206.8638 1.171 0.242 -98.68612 583.127 ------------------------------------------------------------------------------
Table 3.3, page 80.
summ water81 water80 peop81 cpeop retire Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- water81 | 496 2298.387 1486.123 100 10100 water80 | 496 2732.056 1763.8 200 12700 peop81 | 496 3.072581 1.657177 1 10 cpeop | 496 -.0383065 .4846579 -3 3 retire | 496 .2943548 .4562123 0 1
regress water81 water80 peop81 cpeop retire Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 4, 491) = 229.91 Model | 712718346 4 178179587 Prob > F = 0.0000 Residual | 380520363 491 774990.557 R-squared = 0.6519 ---------+------------------------------ Adj R-squared = 0.6491 Total | 1.0932e+09 495 2208563.05 Root MSE = 880.34 ------------------------------------------------------------------------------ water81 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- water80 | .519741 .026774 19.412 0.000 .4671352 .5723468 peop81 | 265.2894 29.63234 8.953 0.000 207.0675 323.5112 cpeop | 134.4626 83.1959 1.616 0.107 -29.00135 297.9265 retire | 67.27992 94.28846 0.714 0.476 -117.9787 252.5386 _cons | 48.64897 107.0549 0.454 0.650 -161.6932 258.9912 ------------------------------------------------------------------------------
To obtain the F-statistic and its corresponding p-value at the top of page 61, first regress the full model with income and educat (quietly suppresses the output). Then use the test statement to test the simpler model which doesn’t have income and educat.
quietly regress water81 water80 peop81 cpeop retire income educat
test income educat
( 1) income = 0.0
( 2) educat = 0.0
F( 2, 489) = 19.24
Prob > F = 0.0000
To obtain the estimates on page 86, first use the wells dataset and generate the natural log of chlor. Then summarize this new ln_chlor variable with and without a condition on deep.
use wells, clear (Lee, NH well test data) gen ln_chlor = log(chlor) (1 missing value generated) label variable ln_chlor "Natural Log of Chloride Concen" summarize ln_chlor if deep==0 Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- ln_chlor | 10 3.7751 1.734293 2.302585 6.522093 summ ln_chlor if deep==1 Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- ln_chlor | 42 3.069318 1.258424 1.098612 6.633318 summ ln_chlor Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- ln_chlor | 52 3.205046 1.372147 1.098612 6.633318
Regression model [3.32], page 86.
regress ln_chlor deep
Source | SS df MS Number of obs = 52
---------+------------------------------ F( 1, 50) = 2.19
Model | 4.02334351 1 4.02334351 Prob > F = 0.1455
Residual | 91.9988551 50 1.8399771 R-squared = 0.0419
---------+------------------------------ Adj R-squared = 0.0227
Total | 96.0221986 51 1.88278821 Root MSE = 1.3565
------------------------------------------------------------------------------
ln_chlor | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
deep | -.705782 .477291 -1.479 0.145 -1.664449 .2528851
_cons | 3.7751 .4289495 8.801 0.000 2.91353 4.636671
------------------------------------------------------------------------------
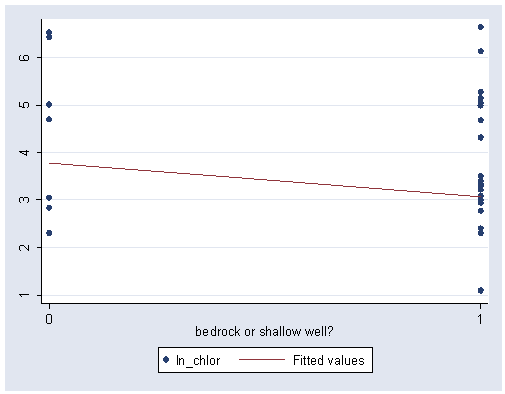
Figure 3.3, page 87.
graph twoway (scatter ln_chlor deep) (lfit ln_chlor deep), ylabel(1(1)6) xlabel(0 1)
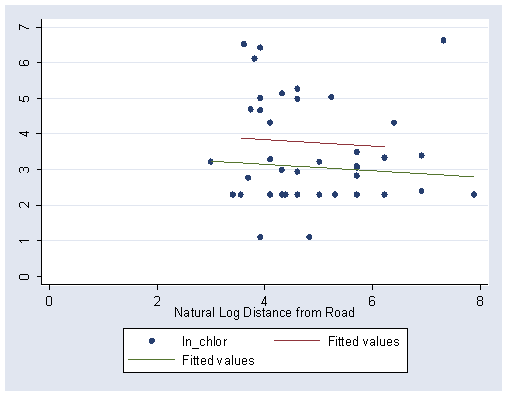
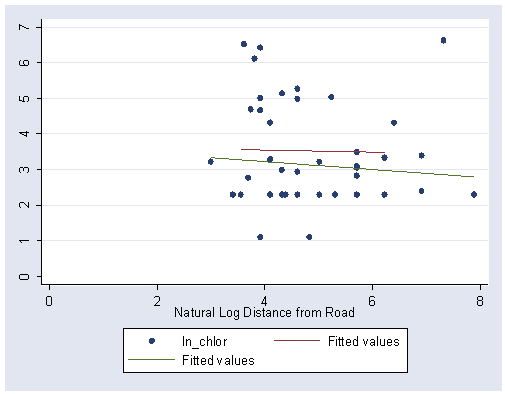
Figure 3.4, page 88. First generate and label the natural log of droad.
gen ln_road = log(droad) label variable ln_road "Natural Log Distance from Road"
Next regress model [3.33] and output the predicted values to yhat.
regress ln_chlor deep ln_road
Source | SS df MS Number of obs = 52
---------+------------------------------ F( 2, 49) = 1.21
Model | 4.50187596 2 2.25093798 Prob > F = 0.3084
Residual | 91.5203226 49 1.86776169 R-squared = 0.0469
---------+------------------------------ Adj R-squared = 0.0080
Total | 96.0221986 51 1.88278821 Root MSE = 1.3667
------------------------------------------------------------------------------
ln_chlor | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
deep | -.6971194 .4811856 -1.449 0.154 -1.664098 .2698592
ln_road | -.0909673 .1797176 -0.506 0.615 -.4521233 .2701886
_cons | 4.20954 .9609568 4.381 0.000 2.278425 6.140655
------------------------------------------------------------------------------
predict yhat (option xb assumed; fitted values)
graph twoway (scatter ln_chlor ln_road) (line yhat ln_road if deep ==0) /// (line yhat ln_road if deep ==1), ylabel(0(1)7) xlabel(0(2)8)
Generate the intercept dummy variable for model [3.34].
Figure 3.5, page 89. This is graphed in the same manner as figure 3.4, once the interaction term is created and the predicted values for [3.34] are output.
gen deeproad = deep*ln_road quietly regress ln_chlor ln_road deeproad predict yhat2 (option xb assumed; fitted values) graph twoway (scatter ln_chlor ln_road) (line yhat2 ln_road if deep ==0) /// (line yhat2 ln_road if deep ==1), ylabel(0(1)7) xlabel(0(2)8)
Table 3.4, page 3.4.
regress ln_chlor deep ln_road deeproad
Source | SS df MS Number of obs = 52
---------+------------------------------ F( 3, 48) = 3.81
Model | 18.4831272 3 6.1610424 Prob > F = 0.0157
Residual | 77.5390714 48 1.61539732 R-squared = 0.1925
---------+------------------------------ Adj R-squared = 0.1420
Total | 96.0221986 51 1.88278821 Root MSE = 1.271
------------------------------------------------------------------------------
ln_chlor | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
deep | -6.717366 2.094713 -3.207 0.002 -10.92907 -2.505663
ln_road | -1.109424 .3844204 -2.886 0.006 -1.882354 -.3364954
deeproad | 1.255847 .4268777 2.942 0.005 .3975521 2.114143
_cons | 9.073459 1.879384 4.828 0.000 5.294704 12.85221
------------------------------------------------------------------------------
summ ln_chlor deep ln_road deeproad
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
ln_chlor | 52 3.205046 1.372147 1.098612 6.633318
deep | 53 .8113208 .3949977 0 1
ln_road | 53 4.838378 1.06035 2.995732 7.878534
deeproad | 53 3.937289 2.141892 0 7.878534
Figure 3.6 on page 91 can be graphed using the same steps as figures 3.4 and 3.5.
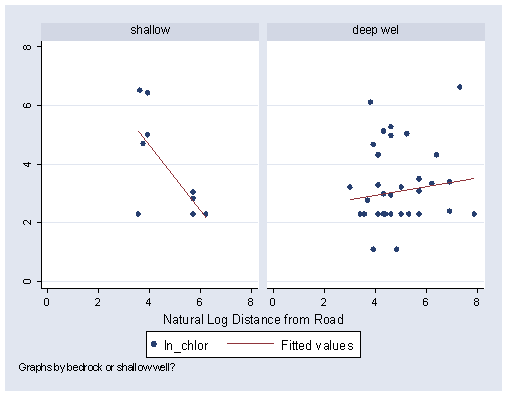
Figure 3.7, page 91.
graph twoway (scatter ln_chlor ln_road) (lfit ln_chlor ln_road, by(deep)), /// xlabel(0(2)8) ylabel(0(2)8)
Regression model [3.38], page 92.
regress ln_chlor ln_road Source | SS df MS Number of obs = 52 ---------+------------------------------ F( 1, 50) = 0.30 Model | .581654392 1 .581654392 Prob > F = 0.5834 Residual | 95.4405442 50 1.90881088 R-squared = 0.0061 ---------+------------------------------ Adj R-squared = -0.0138 Total | 96.0221986 51 1.88278821 Root MSE = 1.3816 ------------------------------------------------------------------------------ ln_chlor | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- ln_road | -.1002276 .1815668 -0.552 0.583 -.4649152 .26446 _cons | 3.691419 .9016771 4.094 0.000 1.880347 5.502491 ------------------------------------------------------------------------------
F-statistic and p-value on page 92.
quietly regress ln_chlor deep ln_road deeproad
test deep deeproad
( 1) deep = 0.0
( 2) deeproad = 0.0
F( 2, 48) = 5.54
Prob > F = 0.0068
Table 3.5, page 93. First use the radon dataset and drop the observations which were not used in the analysis in the book.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/radon, clear (Archer (1987) & Cohen (1988)) drop if _n==10 | _n==15 | _n==16 | _n==21 (4 observations deleted)
Next generate the x1 and x2 dummies.
gen x1=reading gen x2=fringe
Next create area which is a combination of reading, fringe and control. Let area=1 when reading=1. Then recode its missing values if the case is in the fringe or control areas.
gen area=1 if reading==1 /* area=1 if reading */ (20 missing values generated) recode area .=2 if fringe==1 /* area=2 if fringe */ (7 changes made) recode area .=3 if control==1 /* area=3 if control */ (13 changes made) /* adding values labels to "area" */ label define areaname 1 "Reading Prong" 2 "Fringe" 3 "Control" label values area areaname
Next create a new variable mnradon which is a recode of radon. Values 0 – 1.5 are recoded to 1 etc. as in the footnote of Table 3.5.
gen mnradon=radon recode mnradon 0/1.5=1 1.6/2.4=2 2.5/max=3 (26 changes made) label define lmh 1 "Low" 2 "Mid" 3 "High" label values mnradon lmh
Next create the x3 and x4 dummies. These are one if the condition in parenthesis are true and zero otherwise.
gen x3=(mnradon==1) gen x4=(mnradon==2)
View Table 3.5 using list. The pagesize in Stata is not wide enough to view all the variables at once as on page 93.
list county cancer area
county cancer area
1. Orange 6 Reading Prong
2. Putnam 10.5 Reading Prong
3. Sussex 6.7 Reading Prong
4. Warren 6 Reading Prong
5. Morris 6.1 Reading Prong
6. Hunterdon 6.7 Reading Prong
7. Berks 5.2 Fringe
8. Lehigh 5.6 Fringe
9. Northampton 5.8 Fringe
10. Pike 4.5 Fringe
11. Dutchess 5.5 Fringe
12. Sullivan 5.4 Fringe
13. Ulster 6.3 Fringe
14. Columbia 6.3 Control
15. Delaware 4.3 Control
16. Greene 4 Control
17. Otsego 5.9 Control
18. Tioga 4.7 Control
19. Carbon 4.8 Control
20. Lebanon 5.8 Control
21. Lackawanna 5.4 Control
22. Luzerne 5.2 Control
23. Schuylkill 3.6 Control
24. Susquehanna 4.3 Control
25. Wayne 3.5 Control
26. Wyoming 6.9 Control
list county x1 x2 mnradon x3 x4
county x1 x2 mnradon x3 x4
1. Orange 1 0 Low 1 0
2. Putnam 1 0 Mid 0 1
3. Sussex 1 0 Mid 0 1
4. Warren 1 0 High 0 0
5. Morris 1 0 Low 1 0
6. Hunterdon 1 0 High 0 0
7. Berks 0 1 High 0 0
8. Lehigh 0 1 High 0 0
9. Northampton 0 1 High 0 0
10. Pike 0 1 Low 1 0
11. Dutchess 0 1 Mid 0 1
12. Sullivan 0 1 Low 1 0
13. Ulster 0 1 Low 1 0
14. Columbia 0 0 Mid 0 1
15. Delaware 0 0 Mid 0 1
16. Greene 0 0 Mid 0 1
17. Otsego 0 0 Mid 0 1
18. Tioga 0 0 Mid 0 1
19. Carbon 0 0 Mid 0 1
20. Lebanon 0 0 High 0 0
21. Lackawanna 0 0 Low 1 0
22. Luzerne 0 0 Low 1 0
23. Schuylkill 0 0 High 0 0
24. Susquehanna 0 0 Low 1 0
25. Wayne 0 0 Low 1 0
26. Wyoming 0 0 Mid 0 1
The commands for table 3.6 on page 94 and all the other tables following are given by Hamilton in the book or have procedures similar to previous examples. Below are the statements which generate the variables needed.
gen x1x3=x1*x3 gen x1x4=x1*x4 gen x2x3=x2*x3 gen x2x4=x2*x4 gen v1=x1 recode v1 0=-1 if control==1 (13 changes made) gen v2=x2 recode v2 0=-1 if control==1 (13 changes made) gen v3=x3 recode v3 0=-1 if mnradon==3 (7 changes made) gen v4=x4 recode v4 0=-1 if mnradon==3 (7 changes made) gen v2v4=v2*v4 gen v2v3=v2*v3 gen v1v4=v1*v4 gen v1v3=v1*v3
Save the new data.
save radon2, replace