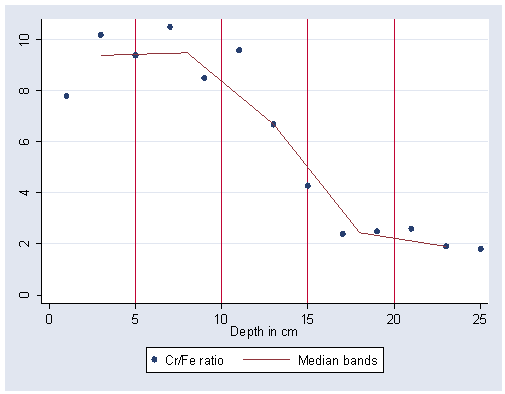
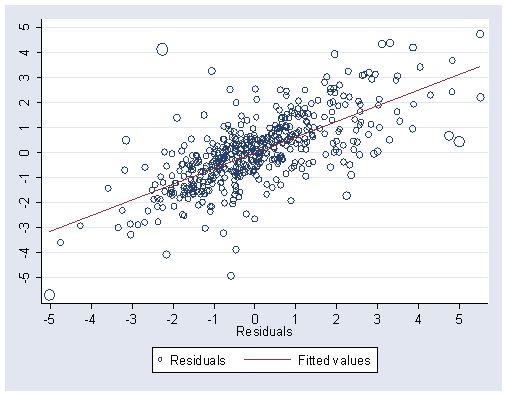
Figure 5.1, page 146.
NOTE: The graph does not match up exactly.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/crfe, clear
graph twoway (scatter crfe depth) (mband crfe depth, band(5)), /// xlabel(0(5)25) ylabel(0(2)10) xline(5 10 15 20)
Table 5.1, page 147. The command egen is used to create the new variables because unlike gen, egen can use functions, such as median, to create variables.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/crfe, clear
gen band=_n
recode band 1/2=1 3/5=2 6/7=3 8/10=4 11/13=5
(12 changes made)
egen mddepth=median(depth), by(band)
egen mdcrfe=median(crfe), by(band)
list depth crfe mddepth mdcrfe
depth crfe mddepth mdcrfe
1. 1 7.8 2 9
2. 3 10.2 2 9
3. 9 8.5 7 9.4
4. 5 9.4 7 9.4
5. 7 10.5 7 9.4
6. 13 6.7 12 8.15
7. 11 9.6 12 8.15
8. 17 2.4 17 2.5
9. 19 2.5 17 2.5
10. 15 4.3 17 2.5
11. 25 1.8 23 1.9
12. 23 1.9 23 1.9
13. 21 2.6 23 1.9
Table 5.2, page 155.
Note: In Stata, ln(x)=log(x), in other words, log(x) defaults to natural log instead of log base 10. If you want log base 10, use log10(x).
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear gen wtr81_3=(water81)^.3 label variable wtr81_3 "water81 to the .3 power" gen wtr80_3=(water80)^.3 label variable wtr80_3 "water80 to the .3 power" gen inc_3=(income)^.3 label variable inc_3 "income to the .3 power" gen logpeop=log(peop81) label variable logpeop "log of peop81" gen clogpeop=log(peop81/peop80) label variable clogpeop "log of peop81/peop80" regress wtr81_3 inc_3 wtr80_3 educat retire logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 6, 489) = 209.51 Model | 1310.1171 6 218.35285 Prob > F = 0.0000 Residual | 509.636644 489 1.04220173 R-squared = 0.7199 ---------+------------------------------ Adj R-squared = 0.7165 Total | 1819.75374 495 3.67627019 Root MSE = 1.0209 ------------------------------------------------------------------------------ wtr81_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- inc_3 | .51572 .1297219 3.976 0.000 .260839 .7706011 wtr80_3 | .6255023 .0290827 21.508 0.000 .5683599 .6826446 educat | -.0361339 .0160111 -2.257 0.024 -.067593 -.0046749 retire | .1013897 .1189905 0.852 0.395 -.132406 .3351855 logpeop | .7146849 .1104854 6.469 0.000 .4976001 .9317696 clogpeop | .9156945 .2627408 3.485 0.001 .3994542 1.431935 _cons | 1.856262 .3849294 4.822 0.000 1.099942 2.612581 ------------------------------------------------------------------------------
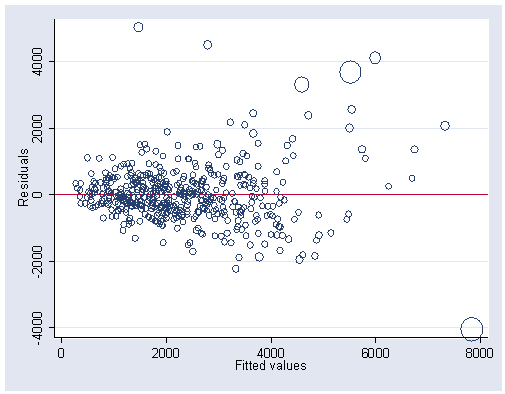
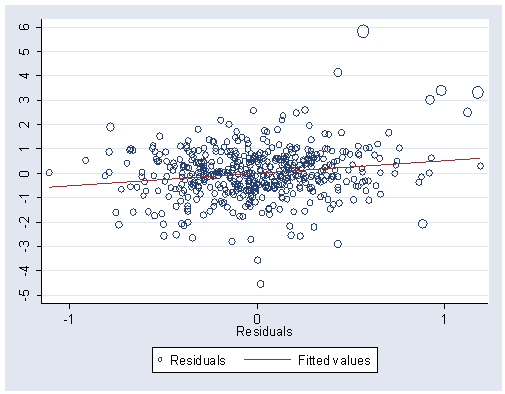
Figure 5.7, page 156.
NOTE: You cannot use the avplot with the [w=d] option, which is why the graph command was used. If you wanted to produce this plot without the scaling (which is the [w=d] option), you could use avplot.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear quietly regress water81 income water80 educat retire peop81 cpeop peop80 predict yhat predict e, residual predict d, cooksd gen cook = . replace cook = (99/4)*d*(d+1)^2 + 1 if d <=1 replace cook = 100 if d >1 graph twoway (scatter e yhat [w=cook], msymbol(oh)), ylabel(-4000(2000)4000) yline(0)
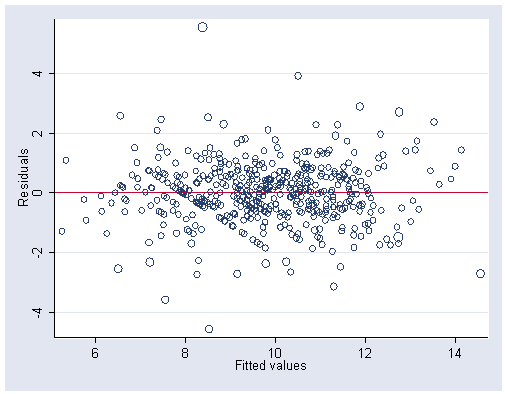
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear gen wtr81_3=(water81)^.3 gen wtr80_3=(water80)^.3 gen inc_3=(income)^.3 gen logpeop=log(peop81) gen clogpeop=log(peop81/peop80) regress wtr81_3 inc_3 wtr80_3 educat retire logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 6, 489) = 209.51 Model | 1310.1171 6 218.35285 Prob > F = 0.0000 Residual | 509.636644 489 1.04220173 R-squared = 0.7199 ---------+------------------------------ Adj R-squared = 0.7165 Total | 1819.75374 495 3.67627019 Root MSE = 1.0209 ------------------------------------------------------------------------------ wtr81_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- inc_3 | .51572 .1297219 3.976 0.000 .260839 .7706011 wtr80_3 | .6255023 .0290827 21.508 0.000 .5683599 .6826446 educat | -.0361339 .0160111 -2.257 0.024 -.067593 -.0046749 retire | .1013897 .1189905 0.852 0.395 -.132406 .3351855 logpeop | .7146849 .1104854 6.469 0.000 .4976001 .9317696 clogpeop | .9156945 .2627408 3.485 0.001 .3994542 1.431935 _cons | 1.856262 .3849294 4.822 0.000 1.099942 2.612581 ------------------------------------------------------------------------------ predict yhat predict e, residual predict d, cooksd gen cook = . replace cook = (99/4)*d*(d+1)^2 + 1 if d <=1 replace cook = 100 if d >1 graph twoway (scatter e yhat [w=cook], msymbol(oh)), ylabel(-4(2)4) xlabel(6(2)14) yline(0)
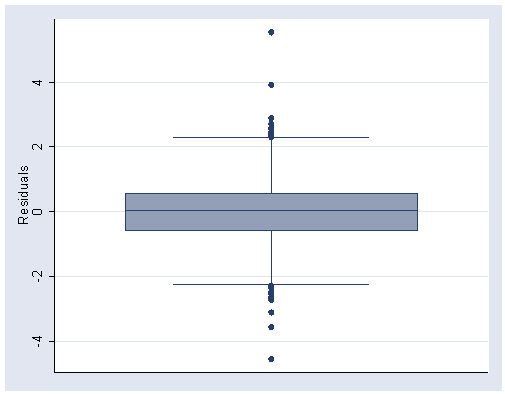
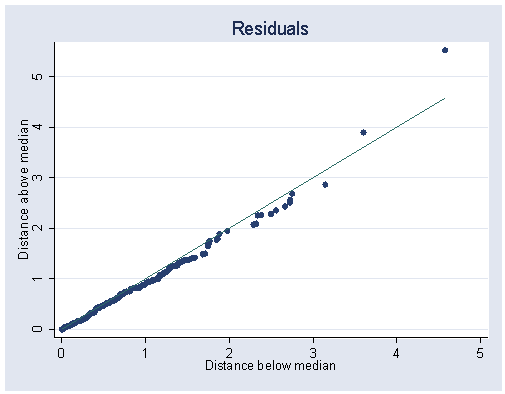
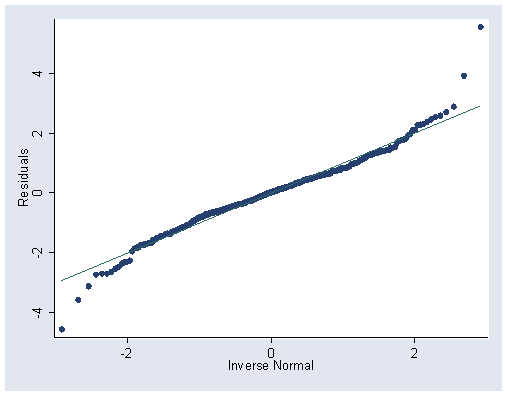
Figure 5.8, page 157.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear gen wtr81_3=(water81)^.3 gen wtr80_3=(water80)^.3 gen inc_3=(income)^.3 gen logpeop=log(peop81) gen clogpeop=log(peop81/peop80) regress wtr81_3 inc_3 wtr80_3 educat retire logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 6, 489) = 209.51 Model | 1310.1171 6 218.35285 Prob > F = 0.0000 Residual | 509.636644 489 1.04220173 R-squared = 0.7199 ---------+------------------------------ Adj R-squared = 0.7165 Total | 1819.75374 495 3.67627019 Root MSE = 1.0209 ------------------------------------------------------------------------------ wtr81_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- inc_3 | .51572 .1297219 3.976 0.000 .260839 .7706011 wtr80_3 | .6255023 .0290827 21.508 0.000 .5683599 .6826446 educat | -.0361339 .0160111 -2.257 0.024 -.067593 -.0046749 retire | .1013897 .1189905 0.852 0.395 -.132406 .3351855 logpeop | .7146849 .1104854 6.469 0.000 .4976001 .9317696 clogpeop | .9156945 .2627408 3.485 0.001 .3994542 1.431935 _cons | 1.856262 .3849294 4.822 0.000 1.099942 2.612581 ------------------------------------------------------------------------------ predict e, residual graph e, norm xlabel(-4 (-2) 4) ylabel(0 (.1) .3) bin(12)
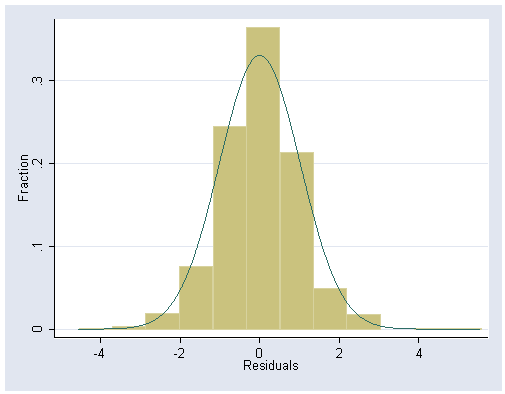
Histogram:
histogram e, norm xlabel(-4(2)4) ylabel(0(.1).3) bin(12) fraction
Boxplot:
graph box e, ylabel(-4(2)4)
Symplot:
symplot e, xlabel(0(1)5) ylabel(0(1)5)
Quantile-normal plot:
qnorm e, ylabel(-4(2)4) xlabel(-2 0 2)
Figure 5.9, page 157.
Note: yresid, xresid, d and y-hat need to be dropped or else Stata will complain that they have already been defined. You can also use the use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear command and re-enter wtr81_3 wtr80_3 and inc_3 instead of dropping yresid, xresid, d and yhat. A third option would be to save the preceding data set with a new name and then to open concord1, saving it with a new name. The clear option was used above (when starting the histogram).
regress wtr81_3 wtr80_3 retire educat logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 5, 490) = 240.97 Model | 1293.64483 5 258.728966 Prob > F = 0.0000 Residual | 526.108911 490 1.07369166 R-squared = 0.7109 ---------+------------------------------ Adj R-squared = 0.7079 Total | 1819.75374 495 3.67627019 Root MSE = 1.0362 ------------------------------------------------------------------------------ wtr81_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- wtr80_3 | .6475596 .0289766 22.348 0.000 .5906259 .7044933 retire | -.0368787 .1155006 -0.319 0.750 -.2638162 .1900588 educat | -.015146 .0153424 -0.987 0.324 -.045291 .014999 logpeop | .779385 .1109189 7.027 0.000 .5614497 .9973204 clogpeop | .9493284 .2665423 3.562 0.000 .4256215 1.473035 _cons | 2.589871 .3428818 7.553 0.000 1.916171 3.263571 ------------------------------------------------------------------------------ predict yresid, residual regress inc_3 wtr80_3 retire educat logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 5, 490) = 58.58 Model | 37.0229573 5 7.40459145 Prob > F = 0.0000 Residual | 61.9334619 490 .12639482 R-squared = 0.3741 ---------+------------------------------ Adj R-squared = 0.3677 Total | 98.9564192 495 .199911958 Root MSE = .35552 ------------------------------------------------------------------------------ inc_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- wtr80_3 | .04277 .009942 4.302 0.000 .0232358 .0623041 retire | -.2681076 .0396286 -6.766 0.000 -.3459706 -.1902446 educat | .0406964 .005264 7.731 0.000 .0303536 .0510393 logpeop | .1254559 .0380566 3.297 0.001 .0506816 .2002303 clogpeop | .0652174 .0914515 0.713 0.476 -.1144681 .244903 _cons | 1.422495 .1176438 12.092 0.000 1.191346 1.653643 ------------------------------------------------------------------------------ predict xresid, residual regress yresid xresid Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 1, 494) = 15.97 Model | 16.4722676 1 16.4722676 Prob > F = 0.0001 Residual | 509.636645 494 1.03165313 R-squared = 0.0313 ---------+------------------------------ Adj R-squared = 0.0293 Total | 526.108913 495 1.06284629 Root MSE = 1.0157 ------------------------------------------------------------------------------ yresid | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- xresid | .51572 .1290637 3.996 0.000 .2621385 .7693016 _cons | -9.38e-10 .0456064 0.000 1.000 -.0896065 .0896065 ------------------------------------------------------------------------------ predict d, cooksd gen cook = . replace cook = (99/4)*d*(d+1)^2 + 1 if d <=1 replace cook = 100 if d >1 graph twoway (scatter yresid xresid [w=cook], msymbol(oh)) (lfit yresid xresid), /// ylabel(-5(1)6) xlabel(-1 0 1)
Figure 5.10, page 158.
drop yresid xresid d yhat regress wtr81_3 inc_3 retire educat logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 5, 490) = 81.82 Model | 828.012394 5 165.602479 Prob > F = 0.0000 Residual | 991.741348 490 2.02396193 R-squared = 0.4550 ---------+------------------------------ Adj R-squared = 0.4495 Total | 1819.75374 495 3.67627019 Root MSE = 1.4227 ------------------------------------------------------------------------------ wtr81_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- inc_3 | 1.047983 .1774549 5.906 0.000 .6993166 1.39665 retire | -.0673496 .1654594 -0.407 0.684 -.3924471 .2577478 educat | -.0387927 .0223117 -1.739 0.083 -.0826312 .0050458 logpeop | 1.842966 .1355056 13.601 0.000 1.576722 2.10921 clogpeop | -.0053465 .3612487 -0.015 0.988 -.7151341 .704441 _cons | 5.949177 .4662837 12.759 0.000 5.033014 6.865339 ------------------------------------------------------------------------------ predict yresid, residual regress wtr80_3 inc_3 retire educat logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 5, 490) = 61.12 Model | 768.524459 5 153.704892 Prob > F = 0.0000 Residual | 1232.20683 490 2.51470781 R-squared = 0.3841 ---------+------------------------------ Adj R-squared = 0.3778 Total | 2000.73129 495 4.04188139 Root MSE = 1.5858 ------------------------------------------------------------------------------ wtr80_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- inc_3 | .850937 .197802 4.302 0.000 .4622922 1.239582 retire | -.2697662 .184431 -1.463 0.144 -.6321394 .0926071 educat | -.0042506 .02487 -0.171 0.864 -.0531157 .0446144 logpeop | 1.8038 .1510427 11.942 0.000 1.507029 2.100572 clogpeop | -1.472482 .4026696 -3.657 0.000 -2.263654 -.6813101 _cons | 6.543406 .519748 12.590 0.000 5.522196 7.564615 ------------------------------------------------------------------------------ predict xresid, residual regress yresid xresid Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 1, 494) = 467.31 Model | 482.1047 1 482.1047 Prob > F = 0.0000 Residual | 509.636644 494 1.03165313 R-squared = 0.4861 ---------+------------------------------ Adj R-squared = 0.4851 Total | 991.741345 495 2.00351787 Root MSE = 1.0157 ------------------------------------------------------------------------------ yresid | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- xresid | .6255023 .0289351 21.617 0.000 .5686512 .6823533 _cons | 1.10e-09 .0456064 0.000 1.000 -.0896065 .0896065 ------------------------------------------------------------------------------ predict yhat predict d, cooksd gen cook = . replace cook = (99/4)*d*(d+1)^2 + 1 if d <=1 replace cook = 100 if d >1 graph twoway (scatter yresid xresid [w=cook], msymbol(oh)) (lfit yresid xresid), /// ylabel(-5(1)5) xlabel(-5(1)5)
Page 159. Means listed at the top of the page.
summarize inc_3 wtr80_3 educat retire logpeop clogpeop Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- inc_3 | 496 2.474998 .4471152 1.231144 3.981072 wtr80_3 | 496 10.29697 2.010443 4.901274 17.02712 educat | 496 14.00403 3.09055 6 20 retire | 496 .2943548 .4562123 0 1 logpeop | 496 .9750739 .5588389 0 2.302585 clogpeop | 496 -.0187373 .1826309 -1.098612 1.386294
This gives Equation [5.14a].
regress wtr81_3 inc_3 wtr80_3 educat retire logpeop clogpeop Source | SS df MS Number of obs = 496 ---------+------------------------------ F( 6, 489) = 209.51 Model | 1310.1171 6 218.35285 Prob > F = 0.0000 Residual | 509.636644 489 1.04220173 R-squared = 0.7199 ---------+------------------------------ Adj R-squared = 0.7165 Total | 1819.75374 495 3.67627019 Root MSE = 1.0209 ------------------------------------------------------------------------------ wtr81_3 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- inc_3 | .51572 .1297219 3.976 0.000 .260839 .7706011 wtr80_3 | .6255023 .0290827 21.508 0.000 .5683599 .6826446 educat | -.0361339 .0160111 -2.257 0.024 -.067593 -.0046749 retire | .1013897 .1189905 0.852 0.395 -.132406 .3351855 logpeop | .7146849 .1104854 6.469 0.000 .4976001 .9317696 clogpeop | .9156945 .2627408 3.485 0.001 .3994542 1.431935 _cons | 1.856262 .3849294 4.822 0.000 1.099942 2.612581 ------------------------------------------------------------------------------
Figure 5.11, page 160.
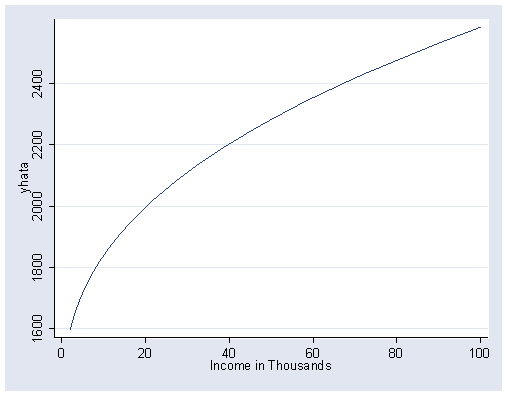
NOTE: Use Equation [5.14b].
gen yhat1=8.507+.516*(income^.3) gen yhata=yhat1^(1/.3) graph twoway line yhata income, sort ylabel(1600(200)2400) xlabel(0(20)100)
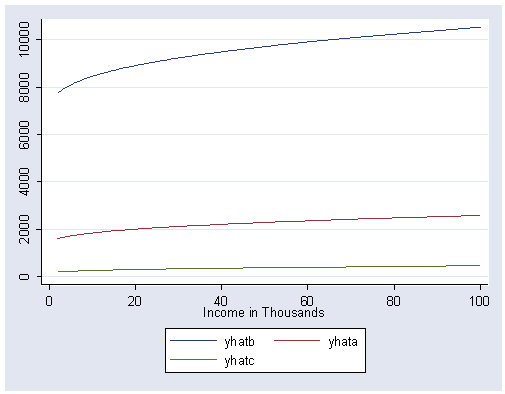
Figure 5.12, page 161.
Top curve:
drop yhat1 yhata gen yhat2=14.046+.516*[income]^.3 gen yhatb=yhat2^(1/.3)
Middle curve:
gen yhat1=8.507+.516*[income]^.3 gen yhata=yhat1^(1/.3)
Bottom curve:
gen yhat3=4.204+.516*[income]^.3 gen yhatc=yhat3^(1/.3) graph twoway (line yhatb income, sort) (line yhata income, sort) (line yhatc income, sort), /// xlabel(0(20)100) ylabel(0(2000)10000)
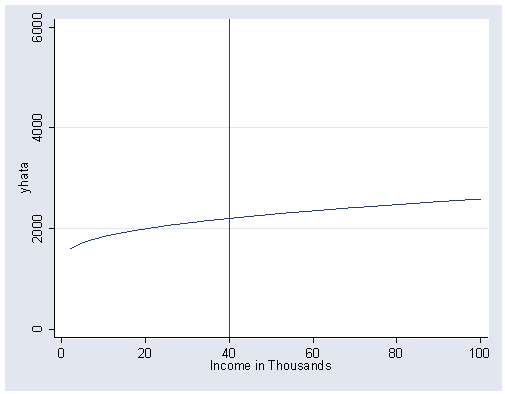
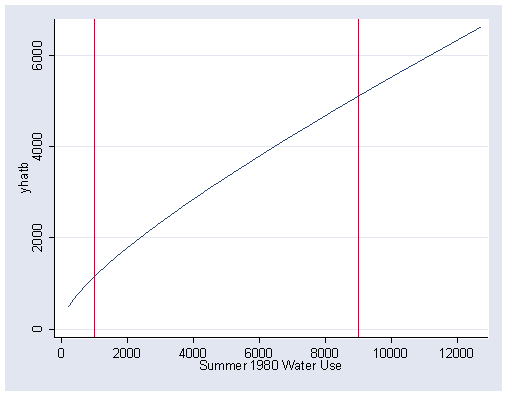
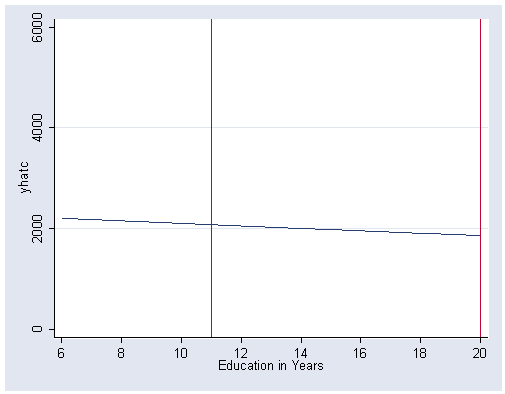
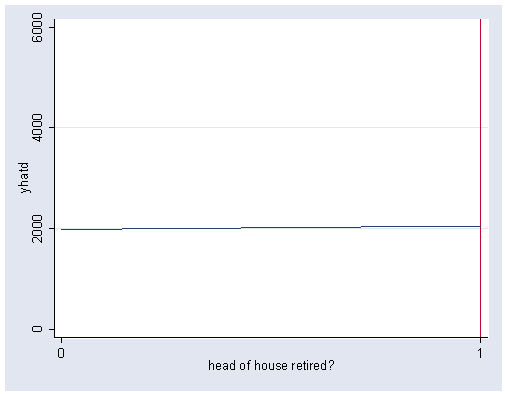
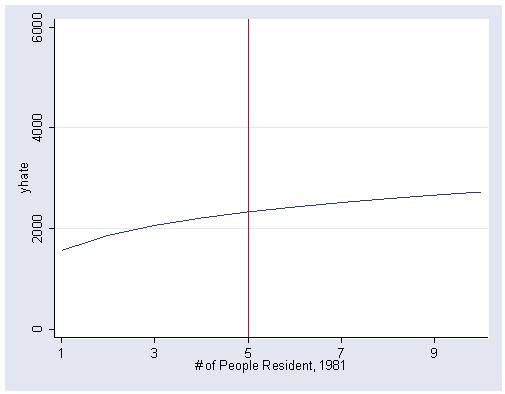
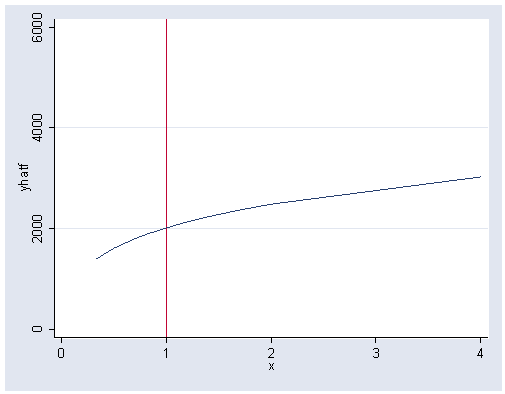
Figure 5.13, page 162.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/concord1, clear
gen yhat1=8.507+.516*(income^.3) gen yhata=yhat1^(1/.3) graph twoway line yhata income, sort xlabel(0(20)100) ylabel(0(2000)6000) xline(40)
gen yhat2=3.338+.626*(water80^.3) gen yhatb=yhat2^(1/.3) graph twoway line yhatb water80, /// sort xlabel(0(2000)12000) ylabel(0(2000)6000) xline(1000 9000)
gen yhat3=10.288-.036*(educat) gen yhatc=yhat3^(1/.3) graph twoway line yhatc educat, sort xlabel(6(2)20) ylabel(0(2000)6000) xline(11 20)
gen yhat4=9.755+.101*(retire) gen yhatd=yhat4^(1/.3) graph twoway line yhatd retire, sort xlabel(0 1) ylabel(0(2000)6000) xline(1)
gen yhat5=9.087+.715*(ln(peop81)) gen yhate=yhat5^(1/.3) graph twoway line yhate peop81, sort xlabel(1(2)10) ylabel(0(2000)6000) xline(5)
gen x=peop81/peop80 gen yhat6=9.802+.916*(ln(x)) gen yhatf=yhat6^(1/.3) graph twoway line yhatf x, sort xlabel(0(1)4) ylabel(0(2000)6000) xline(1)
Table 5.3, page 168. The noobs option tells Stata not to display the observation number, and the nodis option puts the output in the table form used in the book.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/child, clear
list age c1920 c1930 c1940 c1945 c1950 c1955 c1960 if (c1945~=.), noobs nodis
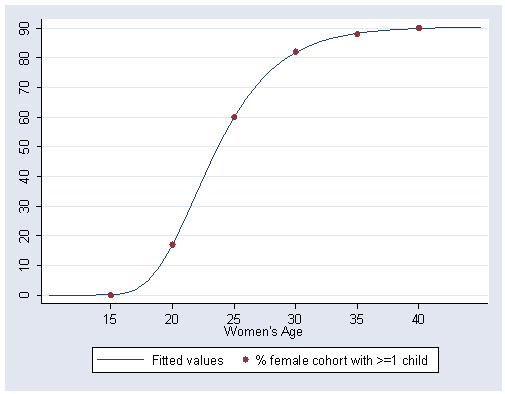
age c1920 c1930 c1940 c1945 c1950 c1955 c1960
15 0 0 0 0 0 0 0
20 7 9 13 17 19 18 13
25 39 48 59 60 53 45 39
30 67 75 82 82 75 68 .
35 76 83 87 88 83 . .
40 78 86 89 90 . . .
Table 5.4, page 169.
Note: Because of differences in the algorithms used by the version of Stata used when creating this table and version 6, fewer iterations are needed to produce the same results. The eps option is forcing Stata to do three more iterations than it would do without the option. Despite the difference in algorithms, the results are the same.
Note that gomh is an .ado program that you need to run before you can use the nl gomh command. The gomh program defines the equation shown at the top of Table 5.4.
program define nlgomh
version 6.0
if "`1'" == "?" {
global S_1 "Alpha Gamma Beta"
global Alpha = 89
global Gamma = 942
global Beta = 0.31
exit
}
replace `1' = $Alpha * exp(-1* $Gamma * exp(-1*$Beta*age))
end
nl gomh c1945, eps(0.00000000001) trace
(obs = 6)
Iteration 0:
Alpha = 89
Gamma = 942
Beta = .31
residual SS = 17.54198
Iteration 1:
Alpha = 89.69356
Gamma = 589.8155
Beta = .2948988
residual SS = 4.928977
Iteration 2:
Alpha = 90.39808
Gamma = 443.0836
Beta = .2808511
residual SS = 1.970012
Iteration 3:
Alpha = 90.42829
Gamma = 465.8808
Beta = .2815535
residual SS = .1213906
Iteration 4:
Alpha = 90.42532
Gamma = 468.054
Beta = .2817029
residual SS = .1184228
Iteration 5:
Alpha = 90.42534
Gamma = 468.0575
Beta = .2817027
residual SS = .1184227
Iteration 6:
Alpha = 90.42534
Gamma = 468.0575
Beta = .2817027
residual SS = .1184227
Iteration 7:
Alpha = 90.42534
Gamma = 468.0575
Beta = .2817027
residual SS = .1184227
Source | SS df MS Number of obs = 6
---------+------------------------------ F( 3, 3) = 223410.65
Model | 26456.8816 3 8818.96053 Prob > F = 0.0000
Residual | .11842265 3 .039474217 R-squared = 1.0000
---------+------------------------------ Adj R-squared = 1.0000
Total | 26457 6 4409.5 Root MSE = .1986812
Res. dev. = -6.524266
(gomh)
------------------------------------------------------------------------------
c1945 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
Alpha | 90.42534 .160669 562.805 0.000 89.91402 90.93666
Gamma | 468.0575 22.54659 20.760 0.000 396.3042 539.8108
Beta | .2817027 .0022184 126.982 0.000 .2746427 .2887628
------------------------------------------------------------------------------
(SE's, P values, CI's, and correlations are asymptotic approximations)
Figure 5.19, page 169.
predict y graph twoway (line y age, sort) (scatter c1945 age), ylabel(0(10)90) xlabel(15(5)40)
Table 5.5, page 170.
nl gomh c1945, iter(10)
(obs = 6)
Iteration 0: residual SS = 17.54198
Iteration 1: residual SS = 4.928977
Iteration 2: residual SS = 1.970012
Iteration 3: residual SS = .1213906
Iteration 4: residual SS = .1184228
Source | SS df MS Number of obs = 6
---------+------------------------------ F( 3, 3) = 223410.65
Model | 26456.8816 3 8818.96053 Prob > F = 0.0000
Residual | .11842265 3 .039474217 R-squared = 1.0000
---------+------------------------------ Adj R-squared = 1.0000
Total | 26457 6 4409.5 Root MSE = .1986812
Res. dev. = -6.524266
(gomh)
------------------------------------------------------------------------------
c1945 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
Alpha | 90.42534 .1606687 562.806 0.000 89.91402 90.93666
Gamma | 468.0575 22.54646 20.760 0.000 396.3046 539.8104
Beta | .2817027 .0022185 126.982 0.000 .2746426 .2887629
------------------------------------------------------------------------------
(SE's, P values, CI's, and correlations are asymptotic approximations)
predict r, resid
(31 missing values generated)
summarize r, detail
Residuals
-------------------------------------------------------------
Percentiles Smallest
1% -.2409922 -.2409922
5% -.2409922 -.0965911
10% -.2409922 -.0693029 Obs 6
25% -.0965911 .026351 Sum of Wgt. 6
50% -.0214759 Mean -.0143851
Largest Std. Dev. .1530889
75% .1136894 -.0693029
90% .1805354 .026351 Variance .0234362
95% .1805354 .1136894 Skewness -.1699677
99% .1805354 .1805354 Kurtosis 1.92567
* Stata 8 code.
vce, rho
* Stata 9 code and output.
estat vce, rho
Correlation matrix of coefficients of nl model
e(V) | Alpha Gamma Beta
-------------+------------------------------
Alpha | 1.0000
Gamma | -0.5869 1.0000
Beta | -0.6342 0.9927 1.0000
Table 5.6, page 172.
nl gomh c1920 c1930 c1940 c1945 c1950 c1955
(obs = 4)
Iteration 0: residual SS = 665.4337
Iteration 1: residual SS = 492.565
Iteration 2: residual SS = 460.7865
Iteration 3: residual SS = 191.9489
Iteration 4: residual SS = 6.350819
Iteration 5: residual SS = 1.521302
Iteration 6: residual SS = .7325416
Iteration 7: residual SS = .2211592
Iteration 8: residual SS = .0009551
Iteration 9: residual SS = .0008995
Source | SS df MS Number of obs = 4
---------+------------------------------ F( 3, 1) = 2245269.07
Model | 6058.9991 3 2019.66637 Prob > F = 0.0005
Residual | .000899521 1 .000899521 R-squared = 1.0000
---------+------------------------------ Adj R-squared = 1.0000
Total | 6059 4 1514.75 Root MSE = .029992
Res. dev. = -22.24826
(gomh)
------------------------------------------------------------------------------
c1920 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
Alpha | 85.93022 .1436735 598.094 0.001 84.10467 87.75576
Gamma | 254.6832 3.478409 73.218 0.009 210.4859 298.8806
Beta | .2310315 .0006446 358.393 0.002 .2228407 .2392224
------------------------------------------------------------------------------
(SE's, P values, CI's, and correlations are asymptotic approximations)
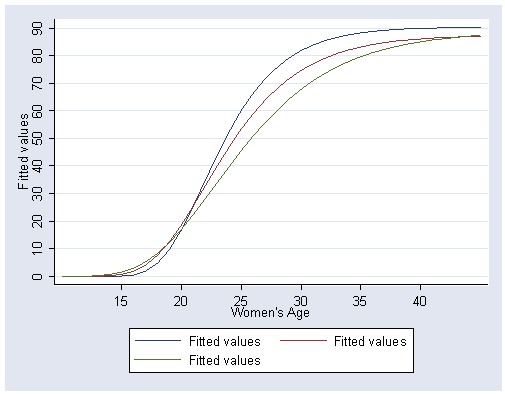
Figure 5.20, page 172.
nl gom3 c1945 age, init(b1=90.4, b2=.28, b3=25.312)
(obs = 6)
Iteration 0: residual SS = 1312.106
Iteration 1: residual SS = 183.3323
Iteration 2: residual SS = 52.10777
Iteration 3: residual SS = .2411037
Iteration 4: residual SS = .1184235
Iteration 5: residual SS = .1184227
Source | SS df MS Number of obs = 6
---------+------------------------------ F( 3, 3) = 223410.65
Model | 26456.8816 3 8818.96053 Prob > F = 0.0000
Residual | .11842265 3 .039474217 R-squared = 1.0000
---------+------------------------------ Adj R-squared = 1.0000
Total | 26457 6 4409.5 Root MSE = .1986812
Res. dev. = -6.524266
3-parameter Gompertz function, c1945=b1*exp(-exp(-b2*(age-b3)))
------------------------------------------------------------------------------
c1945 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
b1 | 90.42534 .1606689 562.806 0.000 89.91402 90.93666
b2 | .2817027 .0022184 126.983 0.000 .2746427 .2887628
b3 | 21.82652 .0207139 1053.713 0.000 21.7606 21.89244
------------------------------------------------------------------------------
(SE's, P values, CI's, and correlations are asymptotic approximations)
predict a, yhat
nl gom3 c1950 age, init(b1=87.5, b2=.23, b3=20.125)
(obs = 5)
Iteration 0: residual SS = 283.4875
Iteration 1: residual SS = 5.771125
Iteration 2: residual SS = .8891598
Iteration 3: residual SS = .8549497
Iteration 4: residual SS = .8549349
Iteration 5: residual SS = .8549348
Source | SS df MS Number of obs = 5
---------+------------------------------ F( 3, 2) = 12229.51
Model | 15683.1451 3 5227.71502 Prob > F = 0.0001
Residual | .854934809 2 .427467404 R-squared = 0.9999
---------+------------------------------ Adj R-squared = 0.9999
Total | 15684 5 3136.8 Root MSE = .6538099
Res. dev. = 5.358545
3-parameter Gompertz function, c1950=b1*exp(-exp(-b2*(age-b3)))
------------------------------------------------------------------------------
c1950 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
b1 | 87.5145 1.021152 85.702 0.000 83.12084 91.90816
b2 | .2271519 .0080141 28.344 0.001 .1926701 .2616337
b3 | 21.9059 .0975443 224.574 0.000 21.48621 22.3256
------------------------------------------------------------------------------
(SE's, P values, CI's, and correlations are asymptotic approximations)
predict b, yhat
nl gom3 c1955 age, init(b1=88.9, b2=.18, b3=16.002)
(obs = 4)
Iteration 0: residual SS = 3039.062
Iteration 1: residual SS = 1012.67
Iteration 2: residual SS = 947.3681
Iteration 3: residual SS = 818.6254
Iteration 4: residual SS = 395.6796
Iteration 5: residual SS = 200.15
Iteration 6: residual SS = 35.09833
Iteration 7: residual SS = 4.517478
Iteration 8: residual SS = 3.492366
Iteration 9: residual SS = 3.489542
Iteration 10: residual SS = 3.489428
Iteration 11: residual SS = 3.489423
Iteration 12: residual SS = 3.489423
Iteration 13: residual SS = 3.489423
Source | SS df MS Number of obs = 4
---------+------------------------------ F( 3, 1) = 665.77
Model | 6969.51058 3 2323.17019 Prob > F = 0.0285
Residual | 3.48942272 1 3.48942272 R-squared = 0.9995
---------+------------------------------ Adj R-squared = 0.9980
Total | 6973 4 1743.25 Root MSE = 1.868
Res. dev. = 10.80528
3-parameter Gompertz function, c1955=b1*exp(-exp(-b2*(age-b3)))
------------------------------------------------------------------------------
c1955 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
b1 | 88.94686 10.49314 8.477 0.075 -44.38107 222.2748
b2 | .1800778 .033323 5.404 0.116 -.243331 .6034866
b3 | 22.76404 .8402734 27.091 0.023 12.08735 33.44073
------------------------------------------------------------------------------
(SE's, P values, CI's, and correlations are asymptotic approximations)
predict c, yhat
graph twoway (line a age, sort) (line b age, sort) (line c age, sort), ///
ylabel(0(10)90) xlabel(15(5)40)