Figure 6.1, page 184.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/airpol, clear
gen lnhc = ln(hc)
label variable lnhc "natural log of hydrocarbon pollution potential"
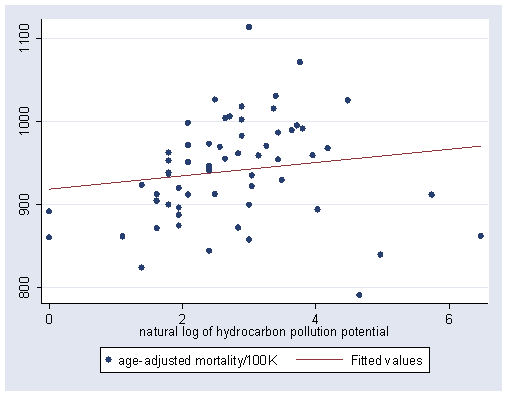
regress mort lnhc
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 1, 58) = 1.35
Model | 5179.87999 1 5179.87999 Prob > F = 0.2506
Residual | 223117.041 58 3846.84554 R-squared = 0.0227
---------+------------------------------ Adj R-squared = 0.0058
Total | 228296.921 59 3869.43934 Root MSE = 62.023
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhc | 7.968576 6.867098 1.160 0.251 -5.777414 21.71457
_cons | 918.4252 20.53273 44.730 0.000 877.3245 959.5259
------------------------------------------------------------------------------
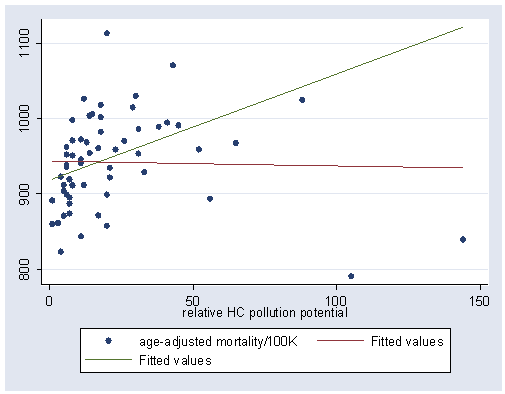
graph twoway (scatter mort lnhc) (lfit mort lnhc), xlabel(0(2)6) ylabel(800(100)1100)
Figure 6.2, page 185.
rreg mort lnhc
Huber iteration 1: maximum difference in weights = .58511763
Huber iteration 2: maximum difference in weights = .12109939
Huber iteration 3: maximum difference in weights = .07054585
Huber iteration 4: maximum difference in weights = .02080019
Biweight iteration 5: maximum difference in weights = .20680335
Biweight iteration 6: maximum difference in weights = .06324705
Biweight iteration 7: maximum difference in weights = .05913415
Biweight iteration 8: maximum difference in weights = .02922746
Biweight iteration 9: maximum difference in weights = .01978239
Biweight iteration 10: maximum difference in weights = .01178611
Biweight iteration 11: maximum difference in weights = .0036652
Robust regression estimates Number of obs = 60
F( 1, 58) = 8.81
Prob > F = 0.0043
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
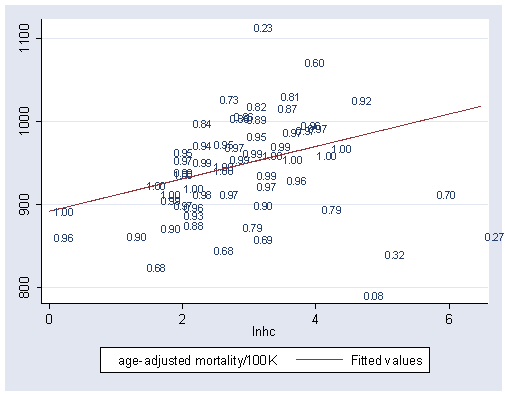
lnhc | 19.45727 6.553716 2.969 0.004 6.338583 32.57596
_cons | 891.75 19.59571 45.507 0.000 852.525 930.9751
------------------------------------------------------------------------------
predict yhat
graph twoway (scatter mort lnhc) (lfit mort lnhc) (line yhat lnhc) ///
(scatter mort lnhc if lnhc >=4.5, mlabel(smsa)), ///
legend(off) xlabel(0(2)6) ylabel(800(100)1100)
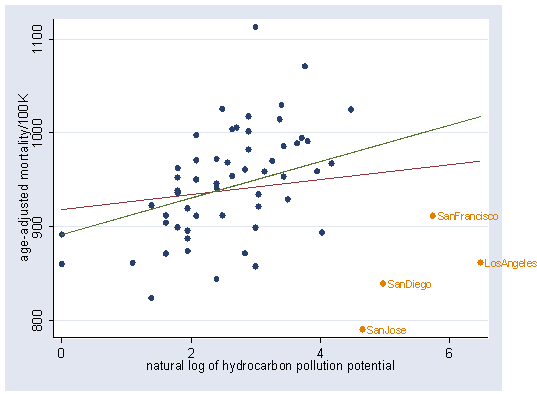
Table 6.1, page186. The genwt option generates the weight and labels it "rweight." The format rweight %3.2f command formats the variable rweight to display only two digits after the decimal.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/airpol, clear
gen lnhc = ln(hc)
rreg mort lnhc, genwt(rweight)
Huber iteration 1: maximum difference in weights = .58511763
Huber iteration 2: maximum difference in weights = .12109939
Huber iteration 3: maximum difference in weights = .07054585
Huber iteration 4: maximum difference in weights = .02080019
Biweight iteration 5: maximum difference in weights = .20680335
Biweight iteration 6: maximum difference in weights = .06324705
Biweight iteration 7: maximum difference in weights = .05913415
Biweight iteration 8: maximum difference in weights = .02922746
Biweight iteration 9: maximum difference in weights = .01978239
Biweight iteration 10: maximum difference in weights = .01178611
Biweight iteration 11: maximum difference in weights = .0036652
Robust regression estimates Number of obs = 60
F( 1, 58) = 8.81
Prob > F = 0.0043
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhc | 19.45727 6.553716 2.969 0.004 6.338583 32.57596
_cons | 891.75 19.59571 45.507 0.000 852.525 930.9751
------------------------------------------------------------------------------
predict yhat
predict e, r
sort rweight
format mort yhat e lnhc %3.1f
format rweight %3.2f
list smsa hc mort yhat e rweight
smsa hc mort yhat e rweight
1. SanJose 105 790.7 982.3 -191.6 0.08
2. NewOrleans 20 1113.0 950.0 163.0 0.23
3. LosAngeles 648 861.8 1017.7 -155.9 0.27
4. SanDiego 144 839.7 988.4 -148.7 0.32
5. Baltimore 43 1071.0 964.9 106.1 0.60
6. Wichita 4 823.8 918.7 -94.9 0.68
7. Lancaster 11 844.1 938.4 -94.3 0.68
8. Minneapolis 20 857.6 950.0 -92.4 0.69
9. SanFrancisco 311 911.7 1003.4 -91.7 0.70
10. Richmond 12 1026.0 940.1 85.9 0.73
11. Portland 56 894.0 970.1 -76.1 0.79
12. Denver 17 871.8 946.9 -75.1 0.79
13. Birmingham 30 1030.0 957.9 72.1 0.81
14. Chattanooga 18 1018.0 948.0 70.0 0.82
15. Albany 8 997.9 932.2 65.7 0.84
16. Memphis 15 1006.0 944.4 61.6 0.86
17. Wilmington 14 1004.0 943.1 60.9 0.86
18. Philadelphia 29 1015.0 957.3 57.7 0.87
19. Rochester 7 874.3 929.6 -55.3 0.88
20. Buffalo 18 1002.0 948.0 54.0 0.89
21. GrandRapids 5 871.3 923.1 -51.8 0.90
22. Miami 3 861.4 913.1 -51.7 0.90
23. Seattle 20 899.3 950.0 -50.7 0.90
24. Chicago 88 1025.0 978.9 46.1 0.92
25. Hartford 7 887.5 929.6 -42.1 0.93
26. Greensboro 8 971.1 932.2 38.9 0.94
27. Allentown 6 962.4 926.6 35.8 0.95
28. Atlanta 18 982.3 948.0 34.3 0.95
29. Toledo 11 972.5 938.4 34.1 0.95
30. Worcester 7 895.7 929.6 -33.9 0.96
31. Dallas 1 860.1 891.8 -31.7 0.96
32. NewYork 41 994.6 964.0 30.6 0.96
33. Milwaukee 33 929.2 959.8 -30.6 0.96
34. Akron 21 921.9 951.0 -29.1 0.97
35. Canton 12 912.3 940.1 -27.8 0.97
36. Cleveland 31 986.0 958.6 27.4 0.97
37. Bridgeport 6 899.5 926.6 -27.1 0.97
38. Indianapolis 13 968.7 941.7 27.0 0.97
39. Louisville 38 989.3 962.5 26.8 0.97
40. Houston 6 952.5 926.6 25.9 0.97
41. Pittsburgh 45 991.3 965.8 25.5 0.97
42. York 8 911.8 932.2 -20.4 0.98
43. Springfield 5 904.2 923.1 -18.9 0.99
44. Syracuse 8 950.7 932.2 18.5 0.99
45. Boston 21 934.7 951.0 -16.3 0.99
46. Cincinnati 26 970.5 955.1 15.4 0.99
47. Nashville 17 961.0 946.9 14.1 0.99
48. Providence 6 938.5 926.6 11.9 0.99
49. Youngstown 14 954.4 943.1 11.3 0.99
50. Utica 5 912.2 923.1 -10.9 1.00
51. KansasCity 7 919.7 929.6 -9.9 1.00
52. Dayton 6 936.2 926.6 9.6 1.00
53. Detroit 52 959.2 968.6 -9.4 1.00
54. Reading 11 946.2 938.4 7.8 1.00
55. Columbus 23 958.8 952.8 6.0 1.00
56. Washington 65 967.8 973.0 -5.2 1.00
57. StLouis 31 953.6 958.6 -5.0 1.00
58. NewHaven 4 923.2 918.7 4.5 1.00
59. Flint 11 941.2 938.4 2.8 1.00
60. FortWorth 1 891.7 891.8 -0.1 1.00
Figure 6.3, page 188.
format rweight %3.2f graph twoway (scatter mort lnhc, mlabel(rweight) msymbol(i)) /// (line yhat lnhc), xlabel(0(2)6) ylabel(800(100)1100)
Figure 6.7, page 197.
NOTE: For the following figure, we are going to produce each graph manually. One can specify the graph option in the rreg command to get a slideshow of the changes in weights in the IRLS estimation.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/airpol, clear
Iteration 1
gen lnhc = ln(hc)
regress mort lnhc
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 1, 58) = 1.35
Model | 5179.87999 1 5179.87999 Prob > F = 0.2506
Residual | 223117.041 58 3846.84554 R-squared = 0.0227
---------+------------------------------ Adj R-squared = 0.0058
Total | 228296.921 59 3869.43934 Root MSE = 62.023
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhc | 7.968576 6.867098 1.160 0.251 -5.777414 21.71457
_cons | 918.4252 20.53273 44.730 0.000 877.3245 959.5259
------------------------------------------------------------------------------
predict e, resid
summarize e, detail
Residuals
-------------------------------------------------------------
Percentiles Smallest
1% -164.8106 -164.8106
5% -106.9425 -118.3275
10% -76.94942 -108.2129 Obs 60
25% -40.61413 -105.672 Sum of Wgt. 60
50% 6.803905 Mean 7.55e-08
Largest Std. Dev. 61.49508
75% 40.52672 84.4721
90% 70.31952 87.77363 Variance 3781.645
95% 86.12286 122.6034 Skewness -.0801513
99% 170.7031 170.7031 Kurtosis 3.362466
The median is the 50th percentile, 6.803905
gen m0=6.803905
gen ee=abs(e-m0)
summarize ee, detail
ee
-------------------------------------------------------------
Percentiles Smallest
1% 1.00688 1.00688
5% 2.174106 1.00688
10% 5.724127 1.863093 Obs 60
25% 20.17187 2.485118 Sum of Wgt. 60
50% 35.41085 Mean 47.77389
Largest Std. Dev. 38.82904
75% 65.78219 115.7995
90% 106.3564 125.1314 Variance 1507.694
95% 120.4655 163.8992 Skewness 1.190757
99% 171.6145 171.6145 Kurtosis 4.333584
gen m00=35.41085
gen s0=m00/.6745
gen es0=abs(e)/s0
gen w1=.
(60 missing values generated)
replace w1=1 if es0<=1.345
(48 real changes made)
replace w1=1.345/es0 if es0>1.345
(12 real changes made)
gen z=1
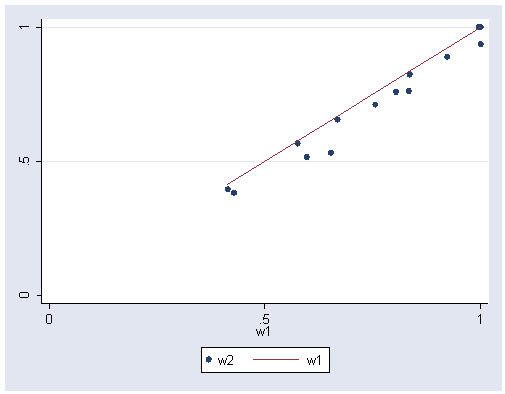
graph twoway scatter w1 z, connect(l) xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 2
gen mortw1=mort*sqrt(w1)
gen lnhcw0=sqrt(w1)
gen lnhcw1=lnhc*sqrt(w1)
regress mortw1 lnhcw1 lnhcw0, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) = 8902.25
Model | 50024076.4 2 25012038.2 Prob > F = 0.0000
Residual | 162958.613 58 2809.63127 R-squared = 0.9968
---------+------------------------------ Adj R-squared = 0.9966
Total | 50187035.0 60 836450.584 Root MSE = 53.006
------------------------------------------------------------------------------
mortw1 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw1 | 12.08538 6.277814 1.925 0.059 -.4810322 24.65179
lnhcw0 | 908.4398 18.31743 49.594 0.000 871.7735 945.1061
------------------------------------------------------------------------------
predict e1, resid
gen e11=e1/lnhcw0
summarize e11, detail
e11
-------------------------------------------------------------
Percentiles Smallest
1% -173.9847 -173.9847
5% -113.1364 -128.8018
10% -78.96231 -124.8792 Obs 60
25% -40.35685 -101.3937 Sum of Wgt. 60
50% 4.943437 Mean -1.349338
Largest Std. Dev. 61.68531
75% 36.87691 80.45545
90% 65.34878 87.52921 Variance 3805.077
95% 83.99233 117.1047 Skewness -.2116352
99% 168.3556 168.3556 Kurtosis 3.577332
gen m1=4.943437
gen ee1=abs(e11-m1)
summarize ee1, detail
ee1
-------------------------------------------------------------
Percentiles Smallest
1% 1.16269 1.16269
5% 1.609889 1.162691
10% 3.902509 1.284287 Obs 60
25% 17.60206 1.935491 Sum of Wgt. 60
50% 33.28572 Mean 47.06011
Largest Std. Dev. 39.91437
75% 63.93033 129.8226
90% 102.2999 133.7453 Variance 1593.157
95% 131.7839 163.4122 Skewness 1.300015
99% 178.9281 178.9281 Kurtosis 4.602989
gen m11= 33.28572gen s1=m11/.6745
gen es1=abs(e11)/s1
gen w2=.
(60 missing values generated)
replace w2=1 if es1<=1.345
(48 real changes made)
replace w2=1.345/es1 if es1>1.345
(12 real changes made)
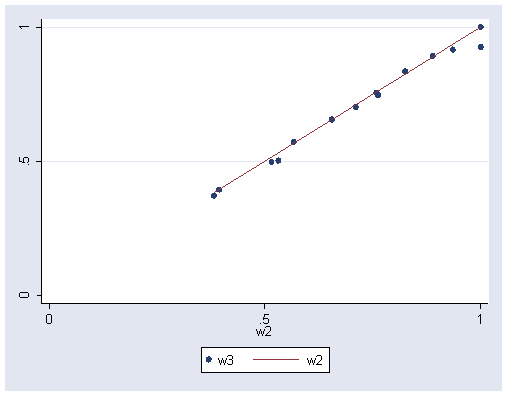
graph twoway (scatter w2 w1) (line w1 w1, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 3
gen mortw2=mort*sqrt(w2)
gen lnhcw2=sqrt(w2)
gen lnhcw3=lnhc*sqrt(w2)
regress mortw2 lnhcw2 lnhcw3, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) = 9248.78
Model | 49588476.9 2 24794238.5 Prob > F = 0.0000
Residual | 155487.033 58 2680.81092 R-squared = 0.9969
---------+------------------------------ Adj R-squared = 0.9968
Total | 49743964.0 60 829066.066 Root MSE = 51.777
------------------------------------------------------------------------------
mortw2 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw2 | 905.4311 18.09045 50.050 0.000 869.2191 941.6431
lnhcw3 | 13.4653 6.237472 2.159 0.035 .9796466 25.95096
------------------------------------------------------------------------------
predict e2, resid
gen e22=e2/lnhcw2
summarize e22, detail
e22
-------------------------------------------------------------
Percentiles Smallest
1% -177.3981 -177.3981
5% -115.551 -132.6511
10% -79.9754 -130.804 Obs 60
25% -40.03335 -100.298 Sum of Wgt. 60
50% 4.820021 Mean -2.139968
Largest Std. Dev. 61.83381
75% 34.83411 78.77076
90% 64.34794 87.10891 Variance 3823.419
95% 82.93983 114.9232 Skewness -.2607152
99% 167.2305 167.2305 Kurtosis 3.656614
gen m2=4.820021
gen ee2=abs(e22-m2)
summarize ee2, detail
ee2
-------------------------------------------------------------
Percentiles Smallest
1% 1.339484 1.339484
5% 2.356566 1.339485
10% 4.189049 1.822319 Obs 60
25% 17.43784 2.890813 Sum of Wgt. 60
50% 32.98885 Mean 46.90808
Largest Std. Dev. 40.43538
75% 62.89881 135.624
90% 101.7788 137.4711 Variance 1635.02
95% 136.5476 162.4104 Skewness 1.342615
99% 182.2181 182.2181 Kurtosis 4.699437
gen m22=32.98885
gen s2=m22/.6745
gen es2=abs(e22)/s2
gen w3=.
(60 missing values generated)
replace w3=1 if es2<=1.345
(47 real changes made)
replace w3=1.345/es2 if es2>1.345
(13 real changes made)
graph twoway (scatter w3 w2) (line w2 w2, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 4
gen mortw3=mort*sqrt(w3)
gen lnhcw4=sqrt(w3)
gen lnhcw5=lnhc*sqrt(w3)
regress mortw3 lnhcw4 lnhcw5, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) = 9332.34
Model | 49471461.0 2 24735730.5 Prob > F = 0.0000
Residual | 153731.199 58 2650.53791 R-squared = 0.9969
---------+------------------------------ Adj R-squared = 0.9968
Total | 49625192.2 60 827086.537 Root MSE = 51.483
------------------------------------------------------------------------------
mortw3 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw4 | 904.103 18.09088 49.976 0.000 867.8902 940.3159
lnhcw5 | 14.08514 6.258612 2.251 0.028 1.557165 26.61311
------------------------------------------------------------------------------
predict e3, resid
gen e33=e3/lnhcw4
summarize e33, detail
e33
-------------------------------------------------------------
Percentiles Smallest
1% -178.9547 -178.9547
5% -116.6589 -134.4035
10% -80.97359 -133.4887 Obs 60
25% -39.90723 -99.82915 Sum of Wgt. 60
50% 4.111221 Mean -2.518487
Largest Std. Dev. 61.91423
75% 34.29168 77.99062
90% 64.13075 86.89668 Variance 3833.372
95% 82.44365 113.92 Skewness -.2834424
99% 166.7017 166.7017 Kurtosis 3.693297
gen m3=4.111221
gen ee3=abs(e33-m3)
summarize ee3, detail
ee3
-------------------------------------------------------------
Percentiles Smallest
1% .7889185 .7889185
5% 2.865521 .7889187
10% 4.604212 2.748589 Obs 60
25% 16.45549 2.982452 Sum of Wgt. 60
50% 33.48549 Mean 46.83978
Largest Std. Dev. 40.58225
75% 61.8055 137.5999
90% 100.9146 138.5147 Variance 1646.919
95% 138.0573 162.5905 Skewness 1.361655
99% 183.0659 183.0659 Kurtosis 4.749048
gen m33=33.48549
gen s3=m33/.6745
gen es3=abs(e33)/s3
gen w4=.
(60 missing values generated)
replace w4=1 if es3<=1.345
(46 real changes made)
replace w4=1.345/es3 if es3>1.345
(14 real changes made)
graph twoway (scatter w4 w3) (line w3 w3, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 5 (change to biweight)
gen mortw4=mort*sqrt(w4)
gen lnhcw6=sqrt(w4)
gen lnhcw7=lnhc*sqrt(w4)
regress mortw4 lnhcw6 lnhcw7, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) = 9291.05
Model | 49565578.2 2 24782789.1 Prob > F = 0.0000
Residual | 154708.151 58 2667.38191 R-squared = 0.9969
---------+------------------------------ Adj R-squared = 0.9968
Total | 49720286.4 60 828671.44 Root MSE = 51.647
------------------------------------------------------------------------------
mortw4 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw6 | 903.8434 18.15556 49.783 0.000 867.5011 940.1857
lnhcw7 | 14.21256 6.283636 2.262 0.027 1.634493 26.79062
------------------------------------------------------------------------------
predict e4, resid
gen e44=e4/lnhcw6
summarize e44, detail
e44
-------------------------------------------------------------
Percentiles Smallest
1% -179.2881 -179.2881
5% -116.9001 -134.7772
10% -81.27055 -134.054 Obs 60
25% -39.77162 -99.74622 Sum of Wgt. 60
50% 3.95209 Mean -2.609724
Largest Std. Dev. 61.93181
75% 34.16674 77.81688
90% 64.08532 86.83968 Variance 3835.549
95% 82.32828 113.7003 Skewness -.2881632
99% 166.5795 166.5795 Kurtosis 3.700915
gen m4=3.95209
gen ee4=abs(e44-m4)
summarize ee4, detail
ee4
-------------------------------------------------------------
Percentiles Smallest
1% .6757395 .6757395
5% 2.970146 .67574
10% 4.538526 2.939001 Obs 60
25% 16.38228 3.00129 Sum of Wgt. 60
50% 33.58758 Mean 46.82574
Largest Std. Dev. 40.61432
75% 61.58075 138.0061
90% 100.737 138.7292 Variance 1649.523
95% 138.3677 162.6274 Skewness 1.365385
99% 183.2402 183.2402 Kurtosis 4.758903
gen m44=33.58758
gen s4=m44/.6745
gen es4=e44/s4
gen w5=.
(60 missing values generated)
replace w5=(1-(es4/4.685)^2)^2 if (abs(e44)/s4)<=4.685
(60 real changes made)
replace w5=0 if (abs(e44)/s4)>4.685
(0 real changes made)
graph twoway (scatter w5 w4) (line w4 w4, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 6
gen mortw5=mort*sqrt(w5)
gen lnhcw8=sqrt(w5)
gen lnhcw9=lnhc*sqrt(w5)
regress mortw5 lnhcw8 lnhcw9, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) =10199.02
Model | 46795992.5 2 23397996.2 Prob > F = 0.0000
Residual | 133060.189 58 2294.1412 R-squared = 0.9972
---------+------------------------------ Adj R-squared = 0.9971
Total | 46929052.7 60 782150.878 Root MSE = 47.897
------------------------------------------------------------------------------
mortw5 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw8 | 900.2209 17.37487 51.812 0.000 865.4413 935.0005
lnhcw9 | 15.63724 6.060739 2.580 0.012 3.505358 27.76913
------------------------------------------------------------------------------
predict e5, resid
gen e55=e5/lnhcw8
summarize e55, detail
e55
-------------------------------------------------------------
Percentiles Smallest
1% -182.296 -182.296
5% -118.1669 -139.6547
10% -83.87064 -138.2351 Obs 60
25% -37.53524 -98.09869 Sum of Wgt. 60
50% 2.892957 Mean -2.909743
Largest Std. Dev. 62.15267
75% 34.47182 76.59371
90% 64.29753 86.92204 Variance 3862.955
95% 81.75788 111.9643 Skewness -.3419659
99% 165.9341 165.9341 Kurtosis 3.78783
gen m5=2.892957
gen ee5=abs(e55-m5)
summarize ee5, detail
ee5
-------------------------------------------------------------
Percentiles Smallest
1% .589726 .589726
5% 2.40177 .5897262
10% 5.645023 1.591628 Obs 60
25% 16.05141 3.211911 Sum of Wgt. 60
50% 32.65288 Mean 46.70808
Largest Std. Dev. 40.97041
75% 61.40457 141.1281
90% 98.751 142.5477 Variance 1678.574
95% 141.8379 163.0411 Skewness 1.408325
99% 185.1889 185.1889 Kurtosis 4.871201
gen m55=32.65288
gen s5=m55/.6745
gen es5=e55/s5
gen w6=.
(60 missing values generated)
replace w6=(1-(es5/4.685)^2)^2 if (abs(e55)/s5)<=4.685
(60 real changes made)
replace w6=0 if (abs(e55)/s5)>4.685
(0 real changes made)
graph twoway (scatter w6 w5) (line w5 w5, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 7 (Note that iterations 7 and 8 are not graphed in the book.)
gen mortw6=mort*sqrt(w6)
gen lnhcw10=sqrt(w6)
gen lnhcw11=lnhc*sqrt(w6)
regress mortw6 lnhcw10 lnhcw11, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) =10569.43
Model | 46495826.3 2 23247913.2 Prob > F = 0.0000
Residual | 127573.451 58 2199.54225 R-squared = 0.9973
---------+------------------------------ Adj R-squared = 0.9972
Total | 46623399.8 60 777056.663 Root MSE = 46.899
------------------------------------------------------------------------------
mortw6 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw10 | 897.4257 17.15824 52.303 0.000 863.0798 931.7717
lnhcw11 | 16.85949 6.015829 2.803 0.007 4.817501 28.90148
------------------------------------------------------------------------------
predict e6, resid
gen e66=e6/lnhcw10
summarize e66, detail
e66
-------------------------------------------------------------
Percentiles Smallest
1% -185.1891 -185.1891
5% -119.2561 -144.7722
10% -86.414 -141.5143 Obs 60
25% -35.92926 -96.99795 Sum of Wgt. 60
50% 2.874535 Mean -3.479797
Largest Std. Dev. 62.3774
75% 34.60612 75.23182
90% 64.16693 86.67999 Variance 3890.94
95% 80.95591 110.1623 Skewness -.3894314
99% 165.0678 165.0678 Kurtosis 3.864709
gen m6=2.874535
gen ee6=abs(e66-m6)
summarize ee6, detail
ee6
-------------------------------------------------------------
Percentiles Smallest
1% .4724467 .4724467
5% 3.736962 .4724476
10% 5.664235 2.87833 Obs 60
25% 15.30565 4.595593 Sum of Wgt. 60
50% 31.832 Mean 46.64581
Largest Std. Dev. 41.46435
75% 61.2924 144.3889
90% 98.25005 147.6468 Variance 1719.292
95% 146.0178 162.1933 Skewness 1.450591
99% 188.0636 188.0636 Kurtosis 4.977333
gen m66=31.832
gen s6=m66/.6745
gen es6=e66/s6
gen w7=.
(60 missing values generated)
replace w7=(1-(es6/4.685)^2)^2 if (abs(e66)/s6)<=4.685
(60 real changes made)
replace w7=0 if (abs(e66)/s6)>4.685
(0 real changes made)
Iteration 8
gen mortw7=mort*sqrt(w7)
gen lnhcw12=sqrt(w7)
gen lnhcw13=lnhc*sqrt(w7)
regress mortw7 lnhcw12 lnhcw13, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) =10952.16
Model | 46220949.9 2 23110475.0 Prob > F = 0.0000
Residual | 122387.492 58 2110.12917 R-squared = 0.9974
---------+------------------------------ Adj R-squared = 0.9973
Total | 46343337.4 60 772388.957 Root MSE = 45.936
------------------------------------------------------------------------------
mortw7 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw12 | 894.7121 16.95266 52.777 0.000 860.7777 928.6466
lnhcw13 | 18.07344 5.972631 3.026 0.004 6.117918 30.02896
------------------------------------------------------------------------------
predict e7, resid
gen e77=e7/lnhcw12
summarize e77, detail
e77
-------------------------------------------------------------
Percentiles Smallest
1% -188.1251 -188.1251
5% -120.4005 -149.9176
10% -89.00262 -144.8338 Obs 60
25% -34.39677 -95.96723 Sum of Wgt. 60
50% 3.291201 Mean -4.108537
Largest Std. Dev. 62.63243
75% 33.61028 73.81649
90% 63.97465 86.37708 Variance 3922.822
95% 80.09678 108.3101 Skewness -.4375264
99% 164.1446 164.1446 Kurtosis 3.942903
gen m7=3.291201
gen ee7=abs(e77-m7)
summarize ee7, detail
ee7
-------------------------------------------------------------
Percentiles Smallest
1% .1415799 .1415799
5% 4.492992 .1415806
10% 6.058385 4.127497 Obs 60
25% 15.0027 4.858488 Sum of Wgt. 60
50% 32.00533 Mean 46.59337
Largest Std. Dev. 42.0805
75% 60.68345 148.125
90% 98.24997 153.2088 Variance 1770.768
95% 150.6669 160.8534 Skewness 1.492862
99% 191.4163 191.4163 Kurtosis 5.089983
gen m77=32.00533
gen s7=m77/.6745
gen es7=e77/s7
gen w8=.
(60 missing values generated)
replace w8=(1-(es7/4.685)^2)^2 if (abs(e77)/s7)<=4.685
(60 real changes made)
replace w8=0 if (abs(e77)/s7)>4.685
(0 real changes made)
Iteration 9
gen mortw8=mort*sqrt(w8)
gen lnhcw14=sqrt(w8)
gen lnhcw15=lnhc*sqrt(w8)
regress mortw8 lnhcw14 lnhcw15, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) =11032.70
Model | 46288732.5 2 23144366.2 Prob > F = 0.0000
Residual | 121672.237 58 2097.79719 R-squared = 0.9974
---------+------------------------------ Adj R-squared = 0.9973
Total | 46410404.7 60 773506.745 Root MSE = 45.802
------------------------------------------------------------------------------
mortw8 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw14 | 893.1722 16.95102 52.691 0.000 859.2411 927.1034
lnhcw15 | 18.78453 5.985631 3.138 0.003 6.802987 30.76607
------------------------------------------------------------------------------
predict e8, resid
gen e88=e8/lnhcw14
summarize e88, detail
e88
-------------------------------------------------------------
Percentiles Smallest
1% -189.8946 -189.8946
5% -121.1205 -152.9813
10% -90.56861 -146.8279 Obs 60
25% -33.54876 -95.41312 Sum of Wgt. 60
50% 3.485634 Mean -4.526487
Largest Std. Dev. 62.79643
75% 32.97723 72.93785
90% 63.81236 86.14997 Variance 3943.392
95% 79.54391 107.1754 Skewness -.4660449
99% 163.5544 163.5544 Kurtosis 3.989447
gen m8=3.485634
gen ee8=abs(e88-m8)
summarize ee8, detail
ee8
-------------------------------------------------------------
Percentiles Smallest
1% .5012119 .5012119
5% 3.871048 .5012128
10% 6.578306 3.243295 Obs 60
25% 14.83559 4.4988 Sum of Wgt. 60
50% 32.01626 Mean 46.58111
Largest Std. Dev. 42.45112
75% 60.54584 150.3135
90% 98.25001 156.4669 Variance 1802.098
95% 153.3902 160.0687 Skewness 1.518493
99% 193.3803 193.3803 Kurtosis 5.161077
gen m88=32.01626
gen s8=m88/.6745
gen es8=e88/s8
gen w9=.
(60 missing values generated)
replace w9=(1-(es8/4.685)^2)^2 if (abs(e88)/s8)<=4.685
(60 real changes made)
replace w9=0 if (abs(e88)/s8)>4.685
(0 real changes made)
graph twoway (scatter w9 w8) (line w8 w8, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 10
gen mortw9=mort*sqrt(w9)
gen lnhcw16=sqrt(w9)
gen lnhcw17=lnhc*sqrt(w9)
regress mortw9 lnhcw16 lnhcw17, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) =11114.84
Model | 46295327.8 2 23147663.9 Prob > F = 0.0000
Residual | 120790.281 58 2082.59105 R-squared = 0.9974
---------+------------------------------ Adj R-squared = 0.9973
Total | 46416118.0 60 773601.967 Root MSE = 45.635
------------------------------------------------------------------------------
mortw9 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw16 | 892.1295 16.92993 52.695 0.000 858.2405 926.0184
lnhcw17 | 19.26631 5.987742 3.218 0.002 7.280545 31.25208
------------------------------------------------------------------------------
predict e9, resid
gen e99=e9/lnhcw16
summarize e99, detail
e99
-------------------------------------------------------------
Percentiles Smallest
1% -191.0941 -191.0941
5% -121.6088 -155.0575
10% -91.63017 -148.1794 Obs 60
25% -32.97474 -95.03825 Sum of Wgt. 60
50% 3.61685 Mean -4.810208
Largest Std. Dev. 62.91361
75% 32.54779 72.342
90% 63.70186 85.99552 Variance 3958.123
95% 79.16876 106.4061 Skewness -.4854825
99% 163.1539 163.1539 Kurtosis 4.021253
gen m9=3.61685
gen ee9=abs(e99-m9)
summarize ee9, detail
ee9
-------------------------------------------------------------
Percentiles Smallest
1% .7448692 .7448692
5% 3.345251 .7448692
10% 6.870948 2.644254 Obs 60
25% 14.72238 4.046248 Sum of Wgt. 60
50% 32.31808 Mean 46.5728
Largest Std. Dev. 42.71478
75% 60.51368 151.7963
90% 98.25004 158.6744 Variance 1824.553
95% 155.2353 159.537 Skewness 1.535109
99% 194.711 194.711 Kurtosis 5.209073
gen m99=32.31808
gen s9=m99/.6745
gen es9=e99/s9
gen w10=.
(60 missing values generated)
replace w10=(1-(es9/4.685)^2)^2 if (abs(e99)/s9)<=4.685
(60 real changes made)
replace w10=0 if (abs(e99)/s9)>4.685
(0 real changes made)
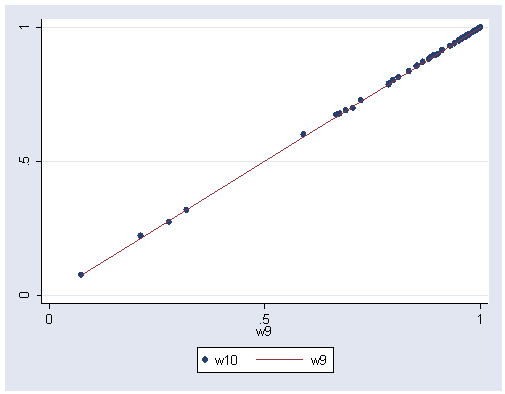
graph twoway (scatter w10 w9) (line w9 w9, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Iteration 11
gen mortw10=mort*sqrt(w10)
gen lnhcw18=sqrt(w10)
gen lnhcw19=lnhc*sqrt(w10)
regress mortw10 lnhcw18 lnhcw19, nocons
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 2, 58) =11069.26
Model | 46399353.4 2 23199676.7 Prob > F = 0.0000
Residual | 121560.159 58 2095.86482 R-squared = 0.9974
---------+------------------------------ Adj R-squared = 0.9973
Total | 46520913.5 60 775348.559 Root MSE = 45.781
------------------------------------------------------------------------------
mortw10 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhcw18 | 891.8404 16.97908 52.526 0.000 857.8531 925.8278
lnhcw19 | 19.41061 6.006624 3.232 0.002 7.387048 31.43418
------------------------------------------------------------------------------
predict e10, resid
gen e1010=e10/lnhcw18
summarize e1010, detail
e1010
-------------------------------------------------------------
Percentiles Smallest
1% -191.4766 -191.4766
5% -121.7784 -155.7027
10% -91.97139 -148.6076 Obs 60
25% -32.82613 -94.94926 Sum of Wgt. 60
50% 3.632838 Mean -4.918479
Largest Std. Dev. 62.94965
75% 32.3959 72.14027
90% 63.64549 85.926 Variance 3962.659
95% 79.03314 106.1523 Skewness -.4913203
99% 163.0105 163.0105 Kurtosis 4.030817
gen m10=3.632838
gen ee10=abs(e1010-m10)
summarize ee10, detail
ee10
-------------------------------------------------------------
Percentiles Smallest
1% .8178842 .8178842
5% 3.119054 .8178847
10% 6.824313 2.464844 Obs 60
25% 14.68851 3.773263 Sum of Wgt. 60
50% 32.40845 Mean 46.57032
Largest Std. Dev. 42.79567
75% 60.50405 152.2404
90% 98.25003 159.3355 Variance 1831.47
95% 155.7879 159.3777 Skewness 1.539966
99% 195.1095 195.1095 Kurtosis 5.2234
gen m1010=32.40845
gen s10=m1010/.6745
gen es10=e1010/s10
gen w11=.
(60 missing values generated)
replace w11=(1-(es10/4.685)^2)^2 if (abs(e1010)/s10)<=4.685
(60 real changes made)
replace w11=0 if (abs(e1010)/s10)>4.685
(0 real changes made)
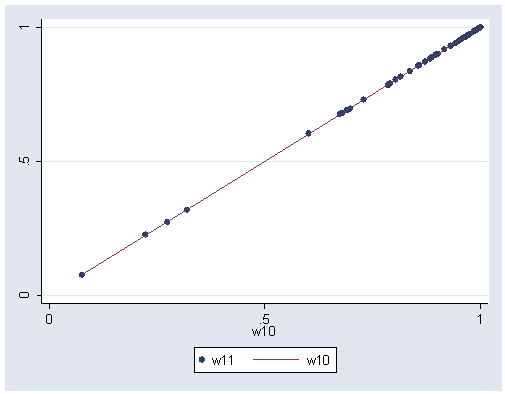
graph twoway (scatter w11 w10) (line w10 w10, sort), xlabel(0 .5 1) ylabel(0 .5 1)
Figure 6.8, page 197.
rreg mort lnhc
Huber iteration 1: maximum difference in weights = .58511763
Huber iteration 2: maximum difference in weights = .12109939
Huber iteration 3: maximum difference in weights = .07054585
Huber iteration 4: maximum difference in weights = .02080019
Biweight iteration 5: maximum difference in weights = .20680335
Biweight iteration 6: maximum difference in weights = .06324705
Biweight iteration 7: maximum difference in weights = .05913415
Biweight iteration 8: maximum difference in weights = .02922746
Biweight iteration 9: maximum difference in weights = .01978239
Biweight iteration 10: maximum difference in weights = .01178611
Biweight iteration 11: maximum difference in weights = .0036652
Robust regression estimates Number of obs = 60
F( 1, 58) = 8.81
Prob > F = 0.0043
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhc | 19.45727 6.553716 2.969 0.004 6.338583 32.57596
_cons | 891.75 19.59571 45.507 0.000 852.525 930.9751
------------------------------------------------------------------------------
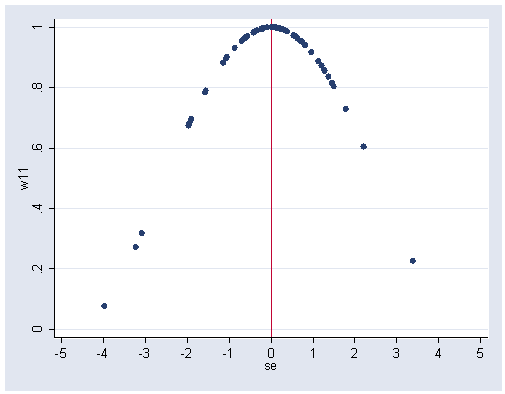
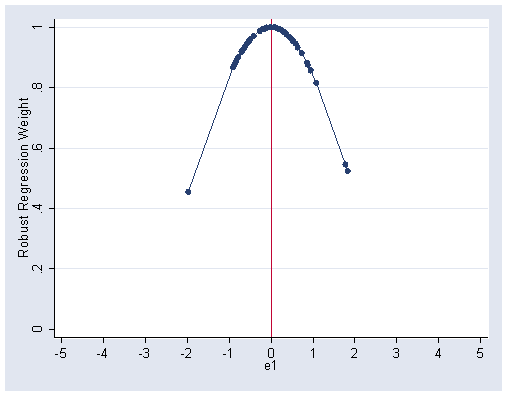
predict e15, r
gen se=e15/48.09
sort se
graph twoway scatter w11 se, xlabel(-5(1)5) ylabel(0(.2)1) xline(0)
Figure 6.9, page 202.
Note: The robust regression line for this graph does not match the book. Further, the next Figure does match when the two outlying points are removed.
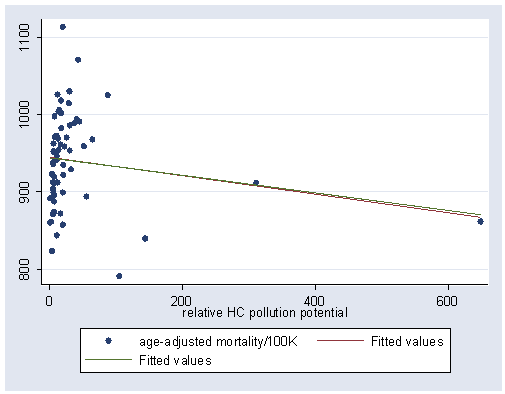
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/airpol, clear
regress mort hc
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 1, 58) = 1.88
Model | 7181.1855 1 7181.1855 Prob > F = 0.1752
Residual | 221115.736 58 3812.34027 R-squared = 0.0315
---------+------------------------------ Adj R-squared = 0.0148
Total | 228296.921 59 3869.43934 Root MSE = 61.744
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
hc | -.1199471 .0873952 -1.372 0.175 -.2948875 .0549934
_cons | 944.905 8.630252 109.488 0.000 927.6297 962.1803
------------------------------------------------------------------------------
predict h, leverage
rreg mort hc, genwt(tempwt)
Huber iteration 1: maximum difference in weights = .47764579
Huber iteration 2: maximum difference in weights = .01386864
Biweight iteration 3: maximum difference in weights = .15809529
Biweight iteration 4: maximum difference in weights = .00210305
Robust regression estimates Number of obs = 60
F( 1, 58) = 1.63
Prob > F = 0.2075
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
hc | -.1138386 .089299 -1.275 0.207 -.2925899 .0649127
_cons | 944.1757 8.818254 107.071 0.000 926.524 961.8273
------------------------------------------------------------------------------
predict yhat2
sort hc
. graph twoway (scatter mort hc) (lfit mort hc) (line yhat2 hc)
Figure 6.10, page 202.
drop if h>=.166
(2 observations deleted)
regress mort hc
Source | SS df MS Number of obs = 58
---------+------------------------------ F( 1, 56) = 0.04
Model | 157.327497 1 157.327497 Prob > F = 0.8424
Residual | 220947.205 56 3945.4858 R-squared = 0.0007
---------+------------------------------ Adj R-squared = -0.0171
Total | 221104.532 57 3879.02688 Root MSE = 62.813
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
hc | -.0636877 .318936 -0.200 0.842 -.7025932 .5752178
_cons | 943.6545 10.95789 86.116 0.000 921.7032 965.6057
------------------------------------------------------------------------------
rreg mort hc
Huber iteration 1: maximum difference in weights = .63453732
Huber iteration 2: maximum difference in weights = .23102242
Huber iteration 3: maximum difference in weights = .04856842
Biweight iteration 4: maximum difference in weights = .26244177
Biweight iteration 5: maximum difference in weights = .10250554
Biweight iteration 6: maximum difference in weights = .01126607
Biweight iteration 7: maximum difference in weights = .00181083
Robust regression estimates Number of obs = 57
F( 1, 55) = 15.93
Prob > F = 0.0002
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
hc | 1.408462 .3529216 3.991 0.000 .7011917 2.115733
_cons | 918.531 10.21261 89.941 0.000 898.0645 938.9975
------------------------------------------------------------------------------
predict yhat6
graph twoway (scatter mort hc) (lfit mort hc) (line yhat6 hc, sort), ///
xlabel(0(50)150) ylabel(800(100)1100)
Figure 6.11, page 204.
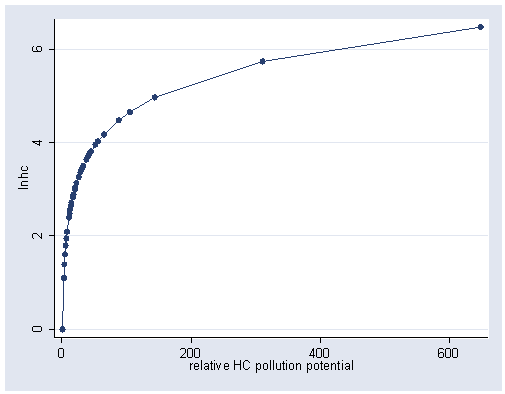
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/airpol, clear gen lnhc = ln(hc) graph twoway scatter lnhc hc, connect(l) sort xlabel(0(200)600) ylabel(0(2)6)
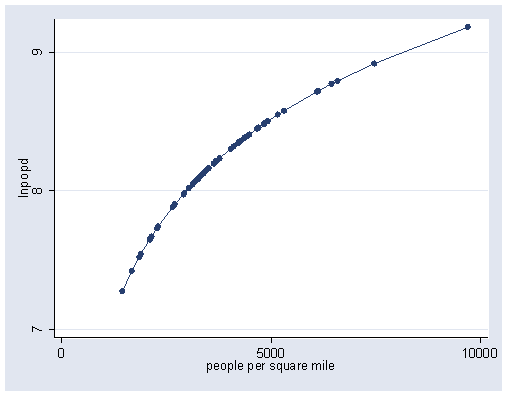
gen lnpopd = ln(popden) graph twoway scatter lnpopd popden, connect(l) sort xlabel(0 5000 10000) ylabel(7 8 9)
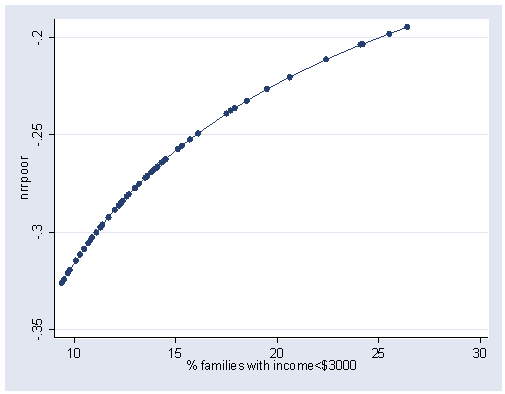
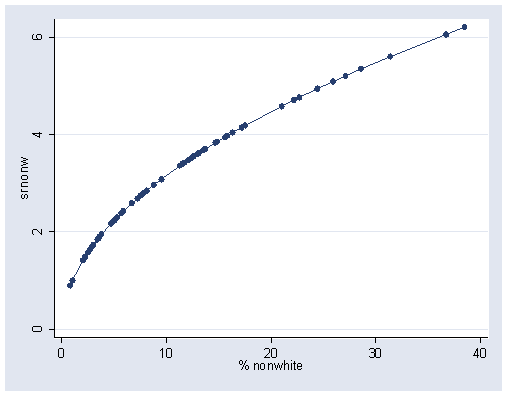
gen nrrpoor = -(1/(sqrt(poor))) graph twoway scatter nrrpoor poor, connect(l) sort xlabel(10(5)30) ylabel(-.35(.05)-.2)
gen srnonw = sqrt(nonw) graph twoway scatter srnonw nonw, connect(l) sort xlabel(0(10)40) ylabel(0(2)6)
Figure 6.12, page 205.
regress mort rain jan educ srnonw
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 4, 55) = 26.00
Model | 149326.539 4 37331.6348 Prob > F = 0.0000
Residual | 78970.3819 55 1435.82513 R-squared = 0.6541
---------+------------------------------ Adj R-squared = 0.6289
Total | 228296.921 59 3869.43934 Root MSE = 37.892
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
rain | 1.038763 .5972583 1.739 0.088 -.1581692 2.235696
jan | -1.9212 .5579225 -3.443 0.001 -3.039302 -.8030985
educ | -21.13074 6.844689 -3.087 0.003 -34.8478 -7.413674
srnonw | 32.40913 4.662617 6.951 0.000 23.06503 41.75322
_cons | 1094.805 86.29434 12.687 0.000 921.8676 1267.743
------------------------------------------------------------------------------
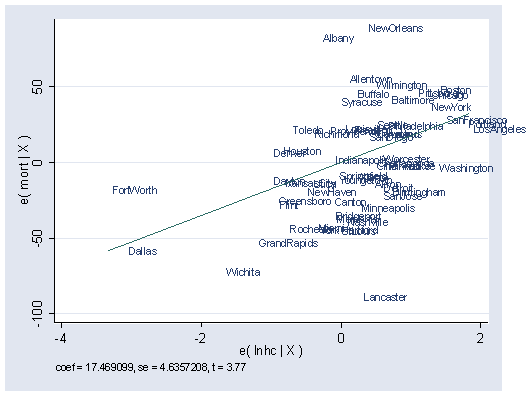
avplot lnhc, mlabel(smsa) msymbol(i) xlabel(-4(2)2) ylabel(-100(50)50)
Figure 6.13, page 206.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/airpol, clear
gen lnhc=log(hc)
gen srnonw=sqrt(nonw)
rreg mort lnhc rain jan educ srnonw, genwt(rweight)
Huber iteration 1: maximum difference in weights = .45915614
Huber iteration 2: maximum difference in weights = .04128307
Biweight iteration 3: maximum difference in weights = .14223798
Biweight iteration 4: maximum difference in weights = .00447933
Robust regression estimates Number of obs = 60
F( 5, 54) = 28.12
Prob > F = 0.0000
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhc | 17.76648 4.625325 3.841 0.000 8.493262 27.0397
rain | 2.317299 .6382043 3.631 0.001 1.037776 3.596821
jan | -2.110483 .5029979 -4.196 0.000 -3.118933 -1.102033
educ | -19.10964 6.190165 -3.087 0.003 -31.52017 -6.699102
srnonw | 26.21364 4.38846 5.973 0.000 17.41531 35.01197
_cons | 1001.758 82.48887 12.144 0.000 836.3781 1167.139
------------------------------------------------------------------------------
predict e, r
gen e1=e/48.09
sort e1
graph twoway scatter rweight e1, connect(l) xlabel(-5(1)5) ylabel(0(.2)1) xline(0)
Table 6.3, page 206.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/airpol, clear
gen lnhc = ln(hc)
gen srnonw = sqrt(nonw)
regress mort lnhc rain jan educ srnonw
Source | SS df MS Number of obs = 60
---------+------------------------------ F( 5, 54) = 28.63
Model | 165769.597 5 33153.9194 Prob > F = 0.0000
Residual | 62527.3244 54 1157.91341 R-squared = 0.7261
---------+------------------------------ Adj R-squared = 0.7008
Total | 228296.921 59 3869.43934 Root MSE = 34.028
------------------------------------------------------------------------------
mort | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
lnhc | 17.4691 4.635721 3.768 0.000 8.175039 26.76316
rain | 2.352107 .6396387 3.677 0.001 1.069709 3.634505
jan | -2.1316 .5041284 -4.228 0.000 -3.142316 -1.120883
educ | -17.95806 6.204078 -2.895 0.005 -30.39649 -5.519631
srnonw | 27.3349 4.398323 6.215 0.000 18.5168 36.15301
_cons | 986.261 82.67427 11.929 0.000 820.509 1152.013
------------------------------------------------------------------------------
predict h, leverage
format h %3.2f
list smsa h if h>.23
smsa h
16. Dallas 0.23
21. FortWorth 0.25
29. LosAngeles 0.28
32. Miami 0.36
46. SanDiego 0.25
Table 6.14, page 209.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/bays, clear
list bay pcb84 pcb85
bay pcb84 pcb85
1. Casco Bay 95.28 77.55
2. Merrimack River 52.97 29.23
3. Salem Harbor 533.58 403.1
4. Boston Harbor 17104.86 736
5. Buzzards' Bay 308.46 192.15
6. Narragansett Bay 159.96 220.6
7. East Long Island Sound 10 8.62
8. West Long Island Sound 234.43 174.31
9. Raritan Bay 443.89 529.28
10. Delaware Bay 2.5 130.67
11. Lower Chesapeake Bay 51 39.74
12. Pamilico Sound 0 0
13. Charleston Harbor 9.1 8.43
14. Sapelo Sound 0 0
15. St. Johns River 140 120.04
16. Tampa Bay 0 0
17. Apalachicola Bay 12 11.93
18. Mobile Bay 0 0
19. Round Island 0 0
20. Mississippi River Delta 34 30.14
21. Barataria Bay 0 0
22. San Antonio Bay 0 0
23. Corpus Christi Bay 0 0
24. San Diego Harbor 422.1 531.67
25. San Diego Bay 6.74 9.3
26. Dana Point 7.06 5.74
27. Seal Beach 46.71 46.47
28. San Pedro Canyon 159.56 176.9
29. Santa Monica Bay 14 13.69
30. Bodega Bay 4.18 4.89
31. Coos Bay 3.19 6.6
32. Columbia River Mouth 8.77 6.73
33. Nisqually Beach 4.23 4.28
34. Commencement Bay 20.6 20.5
35. Elliott Bay 329.97 414.5
36. Lutak Inlet 5.5 5.8
37. Nahku Bay 6.6 5.08
Figure 6.15, page 210.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/bays, clear qreg pcb85 pcb84 Iteration 1: WLS sum of weighted deviations = 3864.9265 Iteration 1: sum of abs. weighted deviations = 16672.456 Iteration 2: sum of abs. weighted deviations = 4312.7581 Iteration 3: sum of abs. weighted deviations = 2969.6801 Median regression Number of obs = 37 Raw sum of deviations 3821.07 (about 11.93) Min sum of deviations 2969.68 Pseudo R2 = 0.2228 ------------------------------------------------------------------------------ pcb85 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- pcb84 | .0425018 .0005854 72.608 0.000 .0413134 .0436901 _cons | 9.013539 9.6191 0.937 0.355 -10.51427 28.54135 ------------------------------------------------------------------------------ predict h1 graph twoway (scatter pcb85 pcb84) (lfit pcb85 pcb84) (line h1 pcb84, sort), /// xlabel(0(4000)16000) ylabel(0(200)800)
Figure 6.16, page 210.
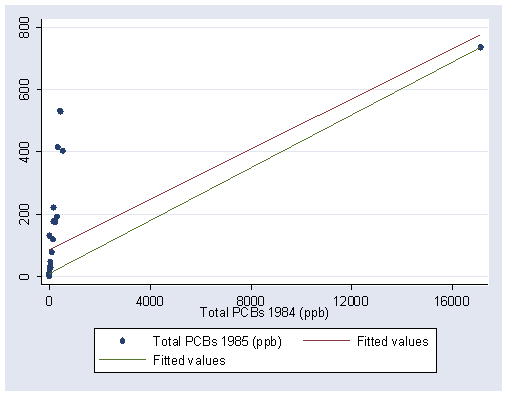
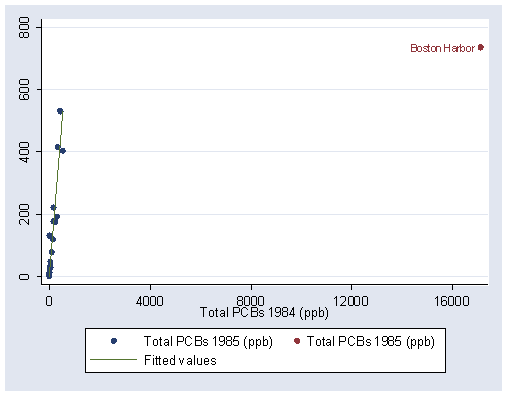
NOTE: The prediction for id #4 is far above the highest point on the scale and is excluded from this analysis so that the line shown in the text can be produced.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/bays, clear
regress pcb85 pcb84
Source | SS df MS Number of obs = 37
---------+------------------------------ F( 1, 35) = 21.77
Model | 462349.858 1 462349.858 Prob > F = 0.0000
Residual | 743254.192 35 21235.8341 R-squared = 0.3835
---------+------------------------------ Adj R-squared = 0.3659
Total | 1205604.05 36 33489.0014 Root MSE = 145.73
------------------------------------------------------------------------------
pcb85 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
pcb84 | .0404537 .0086698 4.666 0.000 .0228532 .0580543
_cons | 85.0138 24.42159 3.481 0.001 35.43533 134.5923
------------------------------------------------------------------------------
predict h, leverage
summarize h, detail
Leverage
-------------------------------------------------------------
Percentiles Smallest
1% .0270276 .0270276
5% .0270645 .0270645
10% .0271934 .0270821 Obs 37
25% .0277486 .0271934 Sum of Wgt. 37
50% .0280503 Mean .0540541
Largest Std. Dev. .1594038
75% .0280756 .0280853
90% .0280853 .0280853 Variance .0254096
95% .0280853 .0280853 Skewness 5.833291
99% .9974615 .9974615 Kurtosis 35.02746
Note that the 90th percentile is .0280853
gen wh=. (37 missing values generated) replace wh=1 if h<=.0280853 (36 real changes made) replace wh=(.0280853/h)^2 if h>.0280853 (1 real change made) qreg pcb85 pcb84 [aw=wh] (sum of wgt is 3.6001e+001) Iteration 1: WLS sum of weighted deviations = 13713.003 (sum of wgt is 3.6001e+001) Iteration 1: sum of abs. weighted deviations = 1122.2417 Iteration 2: sum of abs. weighted deviations = 942.67567 Iteration 3: sum of abs. weighted deviations = 921.36162 Iteration 4: sum of abs. weighted deviations = 921.36163 Median regression Number of obs = 37 Raw sum of deviations 3183.548 (about 11.93) Min sum of deviations 921.3616 Pseudo R2 = 0.7106 ------------------------------------------------------------------------------ pcb85 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- pcb84 | .994862 .0009638 1032.218 0.000 .9929053 .9968186 _cons | -7.92e-07 .1708606 0.000 1.000 -.3468662 .3468646 ------------------------------------------------------------------------------ predict yhat3 if id~=4 (option xb assumed; fitted values) (1 missing value generated) graph twoway (scatter pcb85 pcb84) (line yhat3 pcb84, sort) /// (scatter pcb85 pcb84 if pcb84 >= 16000, mlabel(bay) mlabposition(9)), /// xlabel(0(4000)16000) ylabel(0(200)800)
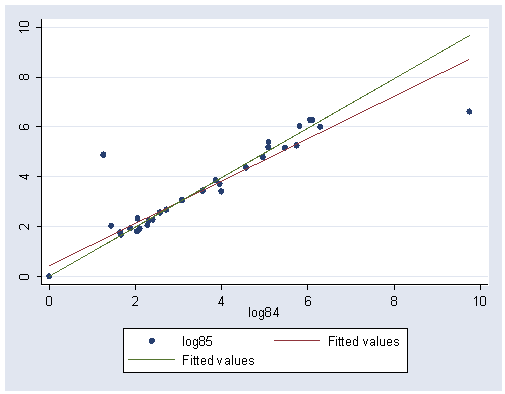
Figure 6.17, page 211.
use https://stats.idre.ucla.edu/stat/stata/examples/rwg/bays, clear
gen log84=log(pcb84+1)
gen log85=log(pcb85+1)
regress log85 log84
Source | SS df MS Number of obs = 37
---------+------------------------------ F( 1, 35) = 251.17
Model | 145.581687 1 145.581687 Prob > F = 0.0000
Residual | 20.2863138 35 .579608967 R-squared = 0.8777
---------+------------------------------ Adj R-squared = 0.8742
Total | 165.868001 36 4.60744448 Root MSE = .76132
------------------------------------------------------------------------------
log85 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
log84 | .8508259 .0536852 15.848 0.000 .741839 .9598127
_cons | .4251097 .202327 2.101 0.043 .014364 .8358553
------------------------------------------------------------------------------
predict h, leverage
summarize h, detail
Leverage
-------------------------------------------------------------
Percentiles Smallest
1% .0270889 .0270889
5% .0273455 .0273455
10% .0286045 .0278075 Obs 37
25% .0311876 .0286045 Sum of Wgt. 37
50% .0415393 Mean .0540541
Largest Std. Dev. .038911
75% .0706273 .0743968
90% .0743968 .0759508 Variance .0015141
95% .0818475 .0818475 Skewness 3.870526
99% .2560128 .2560128 Kurtosis 20.8041
Note that the 90th percentile is .0743968. The [aw=wh] option tells Stata to use wh as the aweight.
gen wh=. (37 missing values generated) replace wh=1 if h<=.0743968 (33 real changes made) replace wh=(.0743968/h)^2 if h>.0743968 (4 real changes made) qreg log85 log84 [aw=wh] (sum of wgt is 3.5870e+001) Iteration 1: WLS sum of weighted deviations = 14.000723 (sum of wgt is 3.5870e+001) Iteration 1: sum of abs. weighted deviations = 11.648956 Iteration 2: sum of abs. weighted deviations = 9.4317616 Iteration 3: sum of abs. weighted deviations = 9.3947206 Median regression Number of obs = 37 Raw sum of deviations 63.89834 (about 2.332144) Min sum of deviations 9.394721 Pseudo R2 = 0.8530 ------------------------------------------------------------------------------ log85 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- log84 | .9922884 .0076806 129.194 0.000 .9766959 1.007881 _cons | -1.49e-09 .0211771 0.000 1.000 -.0429919 .0429919 ------------------------------------------------------------------------------ predict yhat1 graph twoway (scatter log85 log84) (lfit log85 log84) (line yhat1 log84), /// xlabel(0(2)10) ylabel(0(2)10)