The goal in ordinary least squares (OLS) regression is to find the set of regression weight that minimizes the residual sum of squares. There is one, and only one, set of regression weights which minimizes the RSS. At the same time that the RSS is minimized the squared multiple correlation (R2) is maximized. Instead of finding the weights that maximize R2, what if we compute weights that yield R2 – .005, a value very close to R2. According to Waller (2008) there are an infinite number of sets of weights that yield R2 – .005, when there are three or more predictor variables. All of these sets of weights are interchangeable, that is, they are fungible. The program regfungible will compute sets of weights for any degree of reduction in R2 desired (see How can I use the search command to search for programs and get additional help? for more information about using search).
We will demonstrate regfungible using the hsbdemo dataset. We begin by loading the data and then running a regression model with three predictors.
use https://stats.idre.ucla.edu/stat/stata/data/hsbdemo, clear
regress write read math science
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 57.30
Model | 8353.98999 3 2784.66333 Prob > F = 0.0000
Residual | 9524.88501 196 48.5963521 R-squared = 0.4673
-------------+------------------------------ Adj R-squared = 0.4591
Total | 17878.875 199 89.843593 Root MSE = 6.9711
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .2356606 .0691053 3.41 0.001 .0993751 .3719461
math | .3194791 .0756752 4.22 0.000 .1702369 .4687213
science | .2016571 .0690962 2.92 0.004 .0653896 .3379246
_cons | 13.19155 3.068867 4.30 0.000 7.139308 19.24378
------------------------------------------------------------------------------
The R2 for this model is .4673. We want to obtain sets of standardized regression weights for an R2 that is .005 less. The original R2 will be called RSQb, the new reduced R2 is RSQa and the difference between Rsqb and RSQa is theta. Thus,
theta = RSQb - RSQa = .4673 - .005 = .4623
regfungible, sets(200) theta(.005)
OLS fungible regression weights analysis
Original R2: RSQb = .4672548
Reduced R2: RSQa = .4622548
theta = RSQb-RSQa = .005
r_yhata_yhatb = .9946352
Generating Alternate weights ...
Standardized OLS regression weights
1 2 3
+-------------------------------------------+
1 | .2549128629 .3157668631 .2106416581 |
+-------------------------------------------+
Maximum fungible regression weights for each variable
1 2 3
+-------------------------------------------+
1 | .3495532936 .257299223 .1661526516 |
2 | .1970563447 .4079123235 .1626652555 |
3 | .2080402791 .2673600043 .303308868 |
+-------------------------------------------+
Minimum fungible regression weights for each variable
1 2 3
+-------------------------------------------+
1 | .1548185672 .3676814479 .2503990981 |
2 | .3084912273 .2168632372 .2528785178 |
3 | .3008713988 .3528834099 .1136211143 |
+-------------------------------------------+
Summary of fungible regresson weights
stats | v_1 v_2 v_3
---------+------------------------------
N | 200 200 200
mean | .2481542 .3097171 .2154955
min | .1548186 .2168632 .1136211
p25 | .1820209 .249324 .1437956
p50 | .2399547 .3055185 .2210836
p75 | .3167972 .3775634 .2869198
max | .3495533 .4079123 .3033089
----------------------------------------
The output above shows standardized regression weights from the original model (.2549128629, .3157668631, .2106416581). Along with a summary of the new fungible weights which were added to our data. These new variables are labeled by default v_1 through v_3. The prefix for these new variables can be changed using the prefix option in the program.
Looking at the “Summary of fungible regression weights” in the output we see the average, min, max and quartiles for the 200 fungible weights. It is usually more interesting to look at the maximum and minimum weights for each of the variables. For example, the maximum value of v_1 is .3495532936 and is associated with weights .257299223 and .1661526516 for v_2 and v_3 respectively. These weights are rather different from the original weights. And, if we look at the maximum for v_2 (.4079123235) with associated v_1 and v_3 (.1970563447, .1626652555 ) we see that these weights can be very different from each other.
We will now show that these weights generate R2‘s equal to RSQa. We will select the weights for case 255. Note your values will differ from run to run unless you use the seed option.
/* generate standardized predictors */
egen zr = std(read)
egen zm = std(math)
egen zs = std(science)
list v_1 v_2 v_3 in 155
+--------------------------------+
| v_1 v_2 v_3 |
|--------------------------------|
155. | .2216168 .2551833 .3022857 |
+--------------------------------+
generate yhata = .2216168*zr + .2551833*zm + .3022857*zs
corr write yhata
(obs=200)
| write yhata
-------------+------------------
write | 1.0000
yhata | 0.6799 1.0000
display r(rho)^2
.4622548
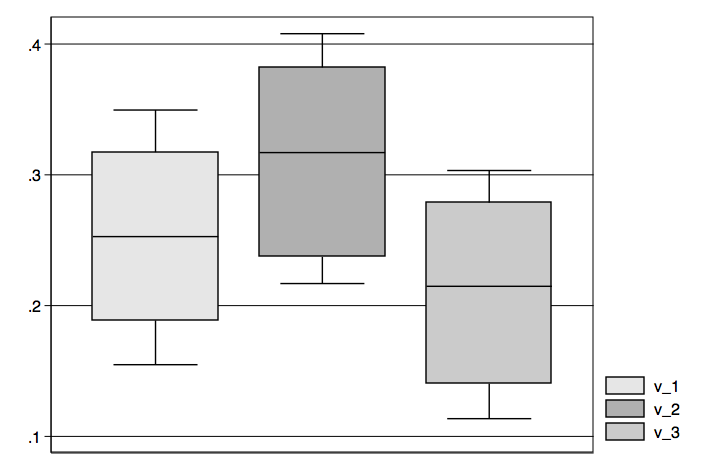
Next, we will generate some graphs from the results of regfungible beginning with a box plot of the regression weights for each variable.
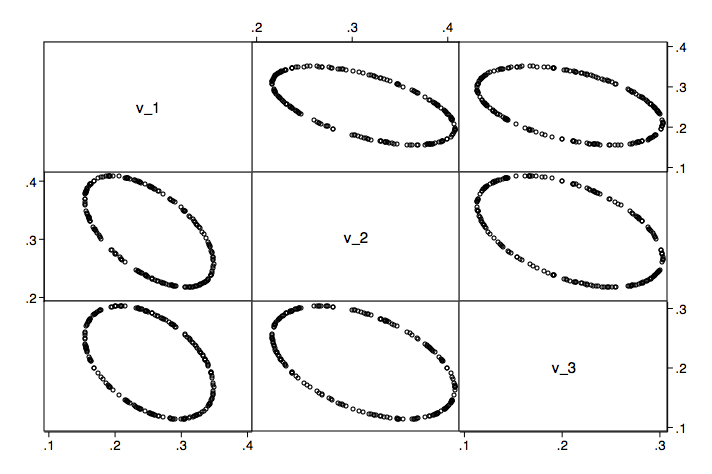
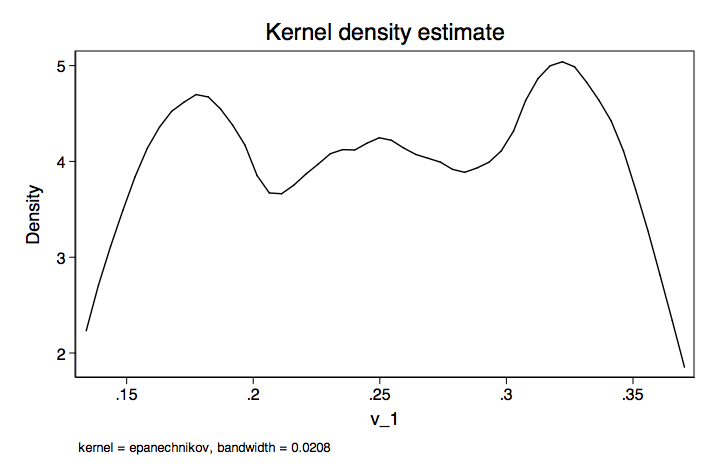
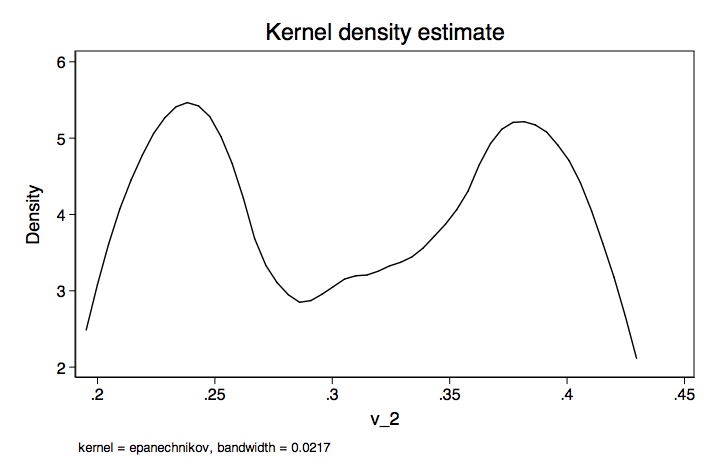
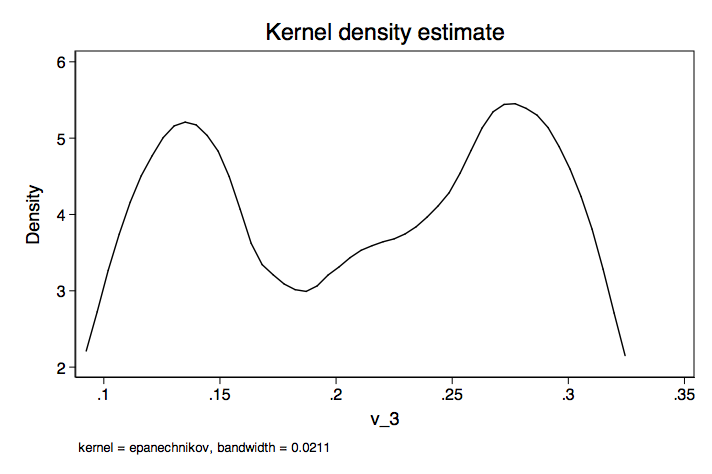
As you can see, there is considerable variability in the regression weights as well as considerable overlap. Next, we will show matrix scatterplot for each of the variables followed by separate kernal density plots for each variable.
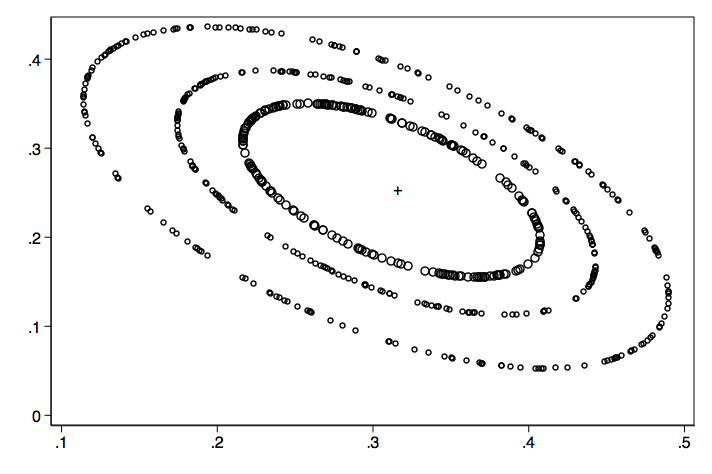
Finally, we plot two variables for three different values of theta: .01, .005 and .001. We end up with something that looks like a solar system model. You can see that as theta gets smaller and smaller the values of the fungible weights converges on the least squares regression weights.