There are times when you want to do correspondence anlysis and the data have been collapsed into a summary with counts for each of the categories. For example, here is a table with the number of degrees given in 12 disciplines over eight different years.
discipline 1960 1965 1970 1971 1972 1973 1974 1975
Agri 414 576 803 900 855 853 830 904
Anth 69 82 217 240 260 324 381 385
Bio 1245 1963 3360 3633 3580 3636 3473 3498
Chem 1078 1444 2234 2204 2011 1849 1792 1762
Earth 253 375 511 550 580 577 570 556
Econ 341 538 826 791 863 907 833 867
Eng 794 2073 3432 3495 3475 3338 3144 2959
Math 291 685 1222 1236 1281 1222 1196 1149
Oth 314 502 1079 1392 1500 1609 1531 1550
Phy 530 1046 1655 1740 1635 1590 134 1293
Psych 772 954 1888 2116 2262 2444 2587 2749
Soc 162 239 504 583 638 599 645 680
We will begin by reading and describing the data.
use https://stats.idre.ucla.edu/stat/data/casummary, clear
describe
Contains data
obs: 12
vars: 9
size: 480 (99.9% of memory free)
-------------------------------------------------------------------------------------------------------------
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------------------------------------
ndisc long %8.0g ndisc
v60 float %9.0g 60 v
v65 float %9.0g 65 v
v70 float %9.0g 70 v
v71 float %9.0g 71 v
v72 float %9.0g 72 v
v73 float %9.0g 73 v
v74 float %9.0g 74 v
v75 float %9.0g 75 v
-------------------------------------------------------------------------------------------------------------
The problem is that we can’t run the ca when the data are in a wide format of summary data. The solution is to reshape the data into long form before running ca with frequency weights. Below you will see the reshape command and a partial listing of the reshaped data.
reshape long v, i(ndisc) j(y)
(note: j = 60 65 70 71 72 73 74 75)
Data wide -> long
-----------------------------------------------------------------------------
Number of obs. 12 -> 96
Number of variables 9 -> 3
j variable (8 values) -> y
xij variables:
v60 v65 ... v75 -> v
-----------------------------------------------------------------------------
clist in 1/15
ndisc y v
1. Agri 60 414
2. Agri 65 576
3. Agri 70 803
4. Agri 71 900
5. Agri 72 855
6. Agri 73 853
7. Agri 74 830
8. Agri 75 904
9. Anth 60 69
10. Anth 65 82
11. Anth 70 217
12. Anth 71 240
13. Anth 72 260
14. Anth 73 324
15. Anth 74 381
Now we are ready to run the correspondence analysis and plot the results.
ca ndisc y [fw=v], norm(principal)
Correspondence analysis Number of obs = 126707
Pearson chi2(77) = 2963.21
Prob > chi2 = 0.0000
Total inertia = 0.0234
12 active rows Number of dim. = 2
8 active columns Expl. inertia (%) = 87.38
| singular principal cumul
Dimension | value inertia chi2 percent percent
------------+------------------------------------------------------------
dim 1 | .1266166 .0160318 2031.34 68.55 68.55
dim 2 | .0663563 .0044032 557.91 18.83 87.38
dim 3 | .0496024 .0024604 311.75 10.52 97.90
dim 4 | .0149596 .0002238 28.36 0.96 98.86
dim 5 | .0128167 .0001643 20.81 0.70 99.56
dim 6 | .0079637 .0000634 8.04 0.27 99.83
dim 7 | .0062852 .0000395 5.01 0.17 100.00
------------+------------------------------------------------------------
total | .0233863 2963.21 100
Statistics for row and column categories in principal normalization
| overall | dimension_1 | dimension_2
Categories | mass quality %inert | coord sqcorr contrib | coord sqcorr contrib
-------------+---------------------------+---------------------------+---------------------------
ndisc | | |
Agri | 0.048 0.725 0.021 | 0.020 0.041 0.001 | 0.084 0.684 0.077
Anth | 0.015 0.925 0.055 | -0.273 0.893 0.072 | -0.052 0.032 0.009
Bio | 0.192 0.845 0.005 | -0.018 0.544 0.004 | 0.013 0.301 0.008
Chem | 0.113 0.983 0.129 | 0.100 0.378 0.071 | 0.127 0.605 0.415
Earth | 0.031 0.725 0.011 | 0.000 0.000 0.000 | 0.078 0.725 0.043
Econ | 0.047 0.462 0.008 | -0.003 0.003 0.000 | 0.043 0.460 0.020
Eng | 0.179 0.107 0.060 | 0.015 0.029 0.003 | -0.025 0.078 0.025
Math | 0.065 0.256 0.016 | -0.020 0.073 0.002 | -0.032 0.183 0.015
Oth | 0.075 0.949 0.102 | -0.147 0.684 0.101 | -0.092 0.265 0.143
Phy | 0.076 0.972 0.444 | 0.346 0.876 0.568 | -0.115 0.096 0.227
Psych | 0.124 0.838 0.122 | -0.139 0.835 0.149 | -0.009 0.004 0.002
Soc | 0.032 0.896 0.026 | -0.122 0.785 0.030 | -0.046 0.112 0.015
-------------+---------------------------+---------------------------+---------------------------
y | | |
60 | 0.049 0.763 0.155 | 0.114 0.178 0.040 | 0.207 0.585 0.480
65 | 0.083 0.900 0.148 | 0.182 0.790 0.170 | 0.068 0.110 0.086
70 | 0.140 0.821 0.080 | 0.105 0.818 0.096 | 0.006 0.002 0.001
71 | 0.149 0.867 0.040 | 0.069 0.769 0.045 | -0.025 0.098 0.021
72 | 0.149 0.883 0.020 | 0.025 0.201 0.006 | -0.046 0.682 0.073
73 | 0.150 0.806 0.033 | -0.011 0.026 0.001 | -0.063 0.780 0.135
74 | 0.135 0.968 0.436 | -0.261 0.904 0.575 | 0.069 0.064 0.148
75 | 0.145 0.635 0.088 | -0.086 0.518 0.067 | -0.041 0.117 0.055
-------------------------------------------------------------------------------------------------
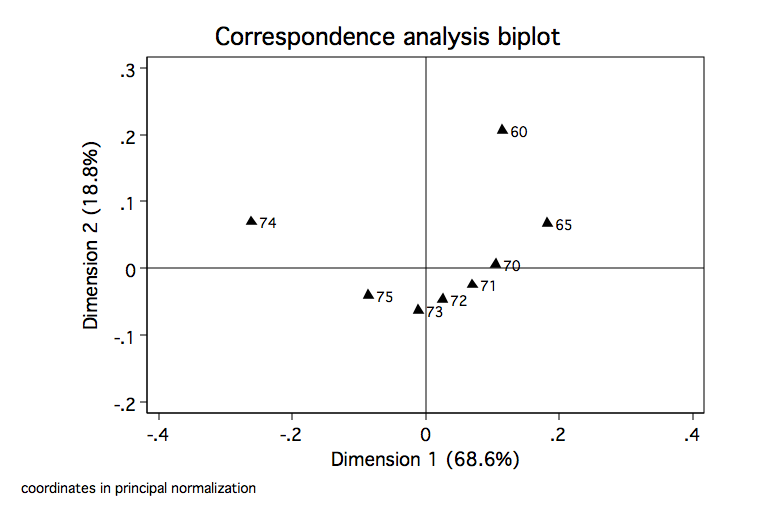
cabiplot, origin
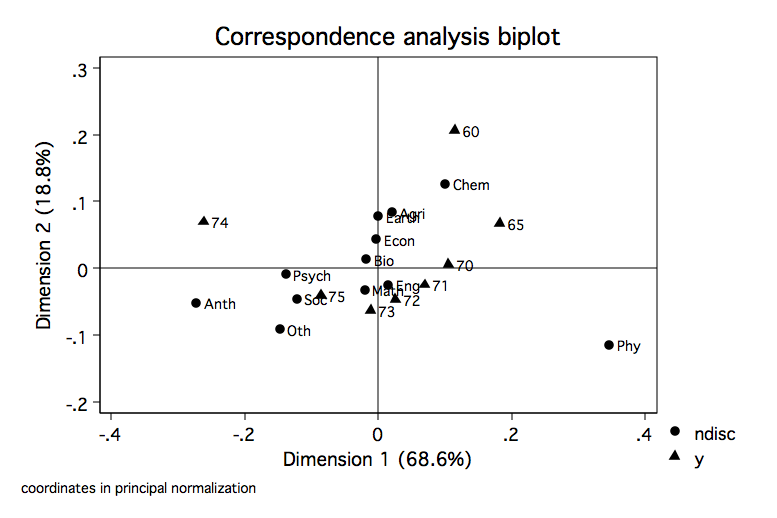cabiplot, origin nocol
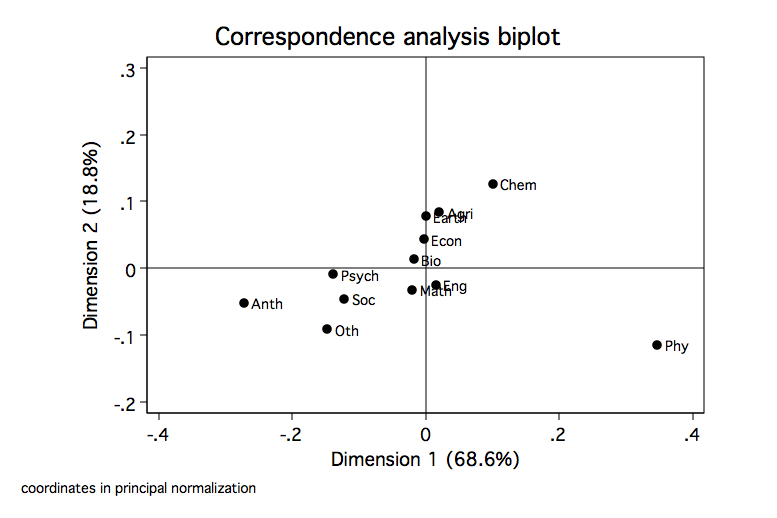cabiplot, origin norow
