Mediator variables are variables that sit between independent variable and dependent variable and mediate the effect of the IV on the DV. Recently, we received a question concerning mediation analysis with a categorical independent variable. A model with a three category independent variable represented by two dummy coded variables is shown in the figure below.
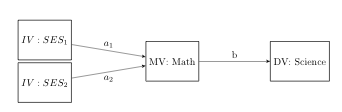
Example 1
This example uses the hsbdemo dataset with science as the DV, ses as the IV and math mediator variable.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
regress science i.ses
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 2, 197) = 8.57
Model | 1561.57802 2 780.789008 Prob > F = 0.0003
Residual | 17945.922 197 91.0960507 R-squared = 0.0801
-------------+------------------------------ Adj R-squared = 0.0707
Total | 19507.5 199 98.0276382 Root MSE = 9.5444
------------------------------------------------------------------------------
science | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ses |
2 | 4.003135 1.702093 2.35 0.020 .6464741 7.359797
3 | 7.746148 1.873189 4.14 0.000 4.052072 11.44022
|
_cons | 47.70213 1.392197 34.26 0.000 44.9566 50.44765
------------------------------------------------------------------------------
testparm i.ses
( 1) 2.ses = 0
( 2) 3.ses = 0
F( 2, 197) = 8.57
Prob > F = 0.0003
regress science math i.ses
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 45.70
Model | 8029.02362 3 2676.34121 Prob > F = 0.0000
Residual | 11478.4764 196 58.563655 R-squared = 0.4116
-------------+------------------------------ Adj R-squared = 0.4026
Total | 19507.5 199 98.0276382 Root MSE = 7.6527
------------------------------------------------------------------------------
science | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math | .6326494 .060202 10.51 0.000 .5139226 .7513763
|
ses |
2 | 2.079683 1.376952 1.51 0.133 -.6358603 4.795226
3 | 3.31621 1.559953 2.13 0.035 .2397611 6.392658
|
_cons | 16.59462 3.16362 5.25 0.000 10.35551 22.83372
------------------------------------------------------------------------------
testparm i.ses
( 1) 2.ses = 0
( 2) 3.ses = 0
F( 2, 196) = 2.29
Prob > F = 0.1038
In the first regression model we see that ses is a significant of science but it is not significant in the second model when the mediator math is added in.
To compute the mediation coefficients we will need the regression coefficients for math on ses and science on both math and ses. The sureg command provides an easy way to get all of the coefficients we need. The general form of the sureg command will look something like this:
sureg (mv i.iv)(dv mv i.iv)
Now, we can begin our mediation analysis.
sureg (math i.ses)(science math i.ses)
Seemingly unrelated regression
----------------------------------------------------------------------
Equation Obs Parms RMSE "R-sq" chi2 P
----------------------------------------------------------------------
math 200 2 8.988521 0.0748 16.18 0.0003
science 200 3 7.575776 0.4116 139.90 0.0000
----------------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
ses |
2 | 3.040314 1.602956 1.90 0.058 -.1014232 6.18205
3 | 7.002201 1.764087 3.97 0.000 3.544654 10.45975
|
_cons | 49.17021 1.311111 37.50 0.000 46.60048 51.73994
-------------+----------------------------------------------------------------
science |
math | .6326494 .0595969 10.62 0.000 .5158416 .7494573
|
ses |
2 | 2.079683 1.363113 1.53 0.127 -.5919687 4.751334
3 | 3.31621 1.544275 2.15 0.032 .2894859 6.342933
|
_cons | 16.59462 3.131824 5.30 0.000 10.45636 22.73288
------------------------------------------------------------------------------
Now we have all the coefficients we need to compute the indirect effect coefficients and their standard errors. We can do this using the nlcom (nonlinear combination) command. We will run nlcom three times: Once for each of the two specific indirect effects for the two dummy coded variables for ses and once for the total indirect effect.
To compute an indirect direct we specify a product of coefficients. For example, the coefficient for math on the first dummy variable for ses is [math]_b[2.ses] and the coefficient for science on math is [science]_b[math]. Thus, the product is [math]_b[2.ses]*[science]_b[math]. To get the total indirect effect we just add the two product terms together in the nlcom command.
/* indirect for 1st dummy coded variable */
nlcom [math]_b[2.ses]*[science]_b[math]
_nl_1: [math]_b[2.ses]*[science]_b[math]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | 1.923453 1.030169 1.87 0.062 -.0956423 3.942548
------------------------------------------------------------------------------
/* indirect for 2nd dummy coded variable */
nlcom [math]_b[3.ses]*[science]_b[math]
_nl_1: [math]_b[3.ses]*[science]_b[math]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | 4.429939 1.191517 3.72 0.000 2.094609 6.765268
------------------------------------------------------------------------------
Next, we will compute the total indirect effect by combining the two nlcoms commands above. We will also save the coefficient in a global macro variable for later use.
/* total indirect */
nlcom [math]_b[2.ses]*[science]_b[math]+[math]_b[3.ses]*[science]_b[math]
_nl_1: [math]_b[2.ses]*[science]_b[math]+[math]_b[3.ses]*[science]_b[math]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | 6.353391 2.002059 3.17 0.002 2.429428 10.27736
------------------------------------------------------------------------------
global indirect=el(r(b),1,1)
We will compute the total direct effect using the lincom command and again save the coefficient in a global macro variable. We do not need to use nlcom for this computation because this is just a simple linear combination of coefficients.
/* total direct */
lincom [science]_b[2.ses]+[science]_b[3.ses]
( 1) [science]2.ses + [science]3.ses = 0
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 5.395892 2.614635 2.06 0.039 .2713013 10.52048
------------------------------------------------------------------------------
global direct=r(estimate)
The results above suggest that each of the second of the indirect effects as well as the total indirect effect are significant. From the above results it is also possible to compute the ratio of indirect to direct effect and the proportion due to the indirect effect. This is where we will make use of the global macro variables. Here are the computations for the ratio of indirect to direct and the proportion of total effect that is mediated.
/* ratio of indirect to direct */ display $indirect/$direct 1.1774496 /* proportion of total effect that is mediated */ display $indirect/($indirect+$direct) .54074712
This computation shows that about 54% of the effect of ses on science is indirect via math.
nlcom computes the standard errors using the delta method which assumes that the estimates of the indirect effect are normally distributed. For many situations this is acceptable but it does not work well for the indirect effects which are usually positively skewed and kurtotic. Thus the z-test and p-values for these indirect effects generally cannot be trusted. Therefore, it is recommended that bootstrap standard errors and confidence intervals be used.
Below is a short ado-program that is called by the bootstrap command. It computes the indirect effect coefficients as the product of sureg coefficients (as before) but does not use the nlcom command since the standard errors will be computed using the bootstrap.
bootcm is an rclass program that produces three return values which we have called “inds2”, “inds3” and “indtotal.” These are the local names for each of the indirect effect coefficients and for the total indirect effect.
We run bootcm with the bootstrap command. We give the bootstrap command the names of the three return values and select options for the number of replications and to omit printing dots after each replication.
Since we selected 5,000 replications you may need to be a bit patient depending upon the speed of your computer.
capture drop program bootcm
program bootcm, rclass
sureg (math i.ses)(science math i.ses)
return scalar inds2 = [math]_b[2.ses]*[science]_b[math]
return scalar inds3 = [math]_b[3.ses]*[science]_b[math]
return scalar indtotal = [math]_b[2.ses]*[science]_b[math] + ///
[math]_b[3.ses]*[science]_b[math]
end
bootstrap r(inds2) r(inds3) r(indtotal), reps(5000) nodots: bootcm
Bootstrap results Number of obs = 200
Replications = 5000
command: bootcm
_bs_1: r(inds2)
_bs_2: r(inds3)
_bs_3: r(indtotal)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | 1.923453 1.02319 1.88 0.060 -.0819636 3.928869
_bs_2 | 4.429939 1.138454 3.89 0.000 2.198609 6.661268
_bs_3 | 6.353391 1.956921 3.25 0.001 2.517897 10.18889
------------------------------------------------------------------------------
We could use the bootstrap standard errors to see if the indirect effects are significant but it is usually recommended that bias-corrected or percentile confidence intervals be used instead. These confidence intervals are nonsymmetric reflecting the skewness of the sampling distribution of the product coefficients. If the confidence interval does not contain zero than the indirect effect is considered to be statistically significant.
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 5000
command: bootcm
_bs_1: r(inds2)
_bs_2: r(inds3)
_bs_3: r(indtotal)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | 1.9234527 -.0103859 1.0231904 -.0391826 3.998063 (P)
| .0513536 4.088075 (BC)
_bs_2 | 4.4299386 -.0114906 1.1384545 2.244273 6.664464 (P)
| 2.284518 6.71173 (BC)
_bs_3 | 6.3533913 -.0218765 1.9569208 2.626967 10.26718 (P)
| 2.719223 10.45621 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
In this example, the total indirect effect of ses through math is significant and, if you go by the biased corrected confidence intervals, so are the individual indirect effects for the two dummy coded variables.
Example 2
What do you do if you also have control variables? You just add them to each of the equations in the sureg model. Let’s say that read is a covariate. Here is how the bootstrap process would work.
capture drop program bootmm
program bootmm, rclass
sureg (math i.ses read)(science math i.ses read)
return scalar inds2 = [math]_b[2.ses]*[science]_b[math]
return scalar inds3 = [math]_b[3.ses]*[science]_b[math]
return scalar indtotal = [math]_b[2.ses]*[science]_b[math] + ///
[math]_b[3.ses]*[science]_b[math]
end
bootstrap r(inds2) r(inds3) r(indtotal), reps(5000) nodots: bootmm
Bootstrap results Number of obs = 200
Replications = 5000
command: bootcm
_bs_1: r(inds2)
_bs_2: r(inds3)
_bs_3: r(indtotal)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .4364702 .5387837 0.81 0.418 -.6195264 1.492467
_bs_2 | .8647798 .6018358 1.44 0.151 -.3147967 2.044356
_bs_3 | 1.30125 1.044232 1.25 0.213 -.7454077 3.347908
------------------------------------------------------------------------------
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 5000
command: bootcm
_bs_1: r(inds2)
_bs_2: r(inds3)
_bs_3: r(indtotal)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .43647022 .015719 .53878367 -.5522534 1.612886 (P)
| -.5350958 1.620241 (BC)
_bs_2 | .86477978 .0177464 .60183578 -.2265526 2.208835 (P)
| -.1950693 2.256182 (BC)
_bs_3 | 1.30125 .0334654 1.0442323 -.5874832 3.572201 (P)
| -.554916 3.640059 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
The addition of the covariate read to the model has changed the situation such that, now, none of the indirect effects are statistically significant.
Reference
Hayes, Andrew F., and Kristopher J. Preacher (2014). Statistical mediation analysis with a multicategorical independent variable. British Journal of Mathematical and Statistical Psychology 67 (3), 451-470.
Preacher, K. J. and Hayes, A. F. 2008. Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behavioral Research Methods, 40, 879-891.
