Preacher, Rucker and Hayes (2007) and updated in Hayes (2013) show how to do moderated mediation using an SPSS macro, so how can I do moderated mediation in Stata?
Here are the full citations:
Hayes, A.F. (2013) Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach. New York, NY: Guilford Press
Preacher, K.J., Rucker, D.D. and Hayes, A.F. (2007). Addressing moderated mediation hypotheses: Theory, methods, and prescriptions. Multivariate Behavioral Research, 42(1), 185-227.
We will begin with a few definitions. A mediator variable is a variable that sits between an independent variable and the dependent variable such that some of the effect of the independent variable on the dependent variable passes through the mediator variable. This is known as the indirect effect.
A moderator variable is a variable involved in an interaction with another variable in the model such that the effect of the other variable depends upon the value of the moderator variable, i.e., the effect of the other variable changes depending on the value of the moderator.
Moderated mediation occurs when a moderator variable interacts with a mediator variable such that the value of the indirect effect changes depending on the value of the moderator variable. This is known as a conditional indirect effect, i.e., the value of the indirect effect is conditional on the value of the moderator variable.
Hayes (2013) and Preacher et al (2007) provide the theoretical background and framework for moderated mediation. They also provide an SPSS script that computes conditional indirect effects and their standard errors in two different ways. It is not all that difficult to compute the indirect effects. On the other hand, standard errors are much more complicated.
The first method in Preacher et al is normal theory based. This method is fairly efficient but suffers from the fact that the distribution of conditional indirect effects are known to be nonnormal, most usually skewed and kurtotic. Confidence intervals and hypothesis tests using normal theory based approaches are not recommended for final models in your research.
The second approach is to use bootstrapping to obtain standard errors and confidence intervals. Although this approach can be much slower the standard errors are not normal theory based. In particular, the biased corrected and percentile confidence intervals are nonsymmetric and better reflect the sampling distribution of the conditional indirect effects.
The remainder of this FAQ page is devoted to showing how to compute conditional indirect effects, standard errors and confidence intervals using Stata. We will show an example for each of the five models from Preacher et al. For each model there is a section using a normal theory based approach that uses sem and nlcom. Also, for each of the models we will show how to obtain the bootstrap estimates of standard errors and confidence intervals.
In order to compute the conditional indirect effects we need to have access to regression coefficients from two different models; one model with the mediator as the response variables and another model with the dependent variable as the response variable. The easiest way to do this in Stata is to use the sem command introduced in Stata 12. When set up correctly, it will have all of the coefficients that we need. In configuring the sem command, all the effects from the mediator variable to the left will go into the first sem equation, while everything from the dependent variable to the left goes into the second sem equation. We will make use of the sem for both the normal based estimation and for bootstrapping.
Conditional indirect effects are obtained by multiplying coefficients from the sem model along with selected values of the moderator variable. For four of the five models, we will compute the conditional indirect effects for three different values of the moderator variable; mean(m1) – 1 sd(m1) {low moderator}, mean(m1) {medium moderator}, mean(m1) + 1 sd(m1) {high moderator}. For model 4 there will be nine combinations of moderator values because the are two moderator variables in the model. Each of the three levels of the first moderator are used in combination with the three levels of the second moderator variable thus yielding the nine combinations.
For the normal based approach we use the nlcom command to compute the conditional indirect effects and their standard errors. nlcom uses the delta method to obtain the standard errors. Each coefficient in the sureg model is identified in nlcom using both the equation name (generally the response variable for that equation) and the predictor name. Thus, in a model with read as the response variable and math as the predictor, the coefficient would by entered as [read]_b[math].
Before trying any of the models, run the Stata code below to read in the data and to rename the variables to be consistent with the variable names in the images of the models. The simplified naming also assists in quickly recognizing the role of each variable in the model.
use https://stats.idre.ucla.edu/stat/data/hsb2, clear rename science y /* dependent variable */ rename math x /* independent variable */ rename read m /* mediator variable */ rename write w /* moderator variable 1 */ rename socst z /* moderator variable 2 */
Note: Model diagrams do not depict all paths and are meant to highlight moderation of the indirect effect only.
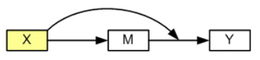
Model 1 (Hayes, 2013 Model 74)
Model 1 illustrates the situation in which the independent variable is also the moderator variable which affects the path between the mediator and the dependent variable.
Formulas:
m = a0 + a1x y = b0 + b1m + b2x + b3mx conditional indirect effect = a1(b1 + b3x)
Normal theory estimation using the delta method for model 1.
quietly summarize x
global m=r(mean)
global s=r(sd)
generate mx=m*x /* mv by iv interaction */
sem (m <- x)(y <- m x mx)
Endogenous variables
Observed: m y
Exogenous variables
Observed: x mx
Fitting target model:
Iteration 0: log likelihood = -3585.6581
Iteration 1: log likelihood = -3585.6581
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -3585.6581
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
m <- |
x | .724807 .0579824 12.50 0.000 .6111636 .8384504
_cons | 14.07254 3.100201 4.54 0.000 7.996255 20.14882
-----------+----------------------------------------------------------------
y <- | m | .9766164 .2875081 3.40 0.001 .4131109 1.540122 x | 1.03094 .2969707 3.47 0.001 .4488881 1.612992 mx | -.0115869 .0053091 -2.18 0.029 -.0219926 -.0011812 _cons | -20.83921 15.16952 -1.37 0.170 -50.57092 8.892495 -------------+---------------------------------------------------------------- var(e.m)| 58.71925 5.871925 48.26811 71.43329 var(e.y)| 49.70994 4.970994 40.86232 60.47326 ------------------------------------------------------------------------------ LR test of model vs. saturated: chi2(1) = 594.37, Prob > chi2 = 0.0000
nlcom _b[m:x]*(_b[y:m]+($m-$s)*_b[y:mx]) /* mean - 1 sd */
_nl_1: _b[m:x]*(_b[y:m]+(52.775-9.47858602138653)*_b[y:mx])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .3442437 .0656135 5.25 0.000 .2156435 .4728439
------------------------------------------------------------------------------
nlcom _b[m:x]*(_b[y:m]+($m)*_b[y:mx]) /* mean */
_nl_1: _b[m:x]*(_b[y:m]+(52.775)*_b[y:mx])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .2646401 .0516905 5.12 0.000 .1633287 .3659515
------------------------------------------------------------------------------
nlcom _b[m:x]*(_b[y:m]+($m+$s)*_b[y:mx]) /* mean + 1 sd */
_nl_1: _b[m:x]*(_b[y:m]+(52.645+9.368447794077296)*_b[y:mx])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1850365 .0614861 3.01 0.003 .064526 .3055469
------------------------------------------------------------------------------
In this example the conditional indirect effect gets smaller as the moderator variable, in this case the independent variable gets larger. Next is the bootstrap code for model 1. The example bootstrap command below uses 500 replications. You will probably want to use at least 1,000 or even 5,000 in real research situations.
capture program drop bootm1
program bootm1, rclass
sem (m <- x)(y <- m x mx)
return scalar cielw = _b[m:x]*(_b[y:m]+($m-$s)*_b[y:mx])
return scalar ciemn = _b[m:x]*(_b[y:m]+($m)*_b[y:mx])
return scalar ciehi = _b[m:x]*(_b[y:m]+($m+$s)*_b[y:mx])
end
bootstrap r(cielw) r(ciemn) r(ciehi), reps(500) nodots: bootm1
Bootstrap results Number of obs = 200
Replications = 500
command: bootm1
_bs_1: r(cielw)
_bs_2: r(ciemn)
_bs_3: r(ciehi)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .3442437 .0596977 5.77 0.000 .2272384 .461249
_bs_2 | .2646401 .0531258 4.98 0.000 .1605154 .3687647
_bs_3 | .1850365 .0637424 2.90 0.004 .0601036 .3099693
------------------------------------------------------------------------------
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 500
command: bootm1
_bs_1: r(cielw)
_bs_2: r(ciemn)
_bs_3: r(ciehi)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .34424374 -.0027403 .05969768 .2204353 .462091 (P)
| .2279064 .4661937 (BC)
_bs_2 | .2646401 -.0008873 .0531258 .1688669 .3666712 (P)
| .172691 .3837206 (BC)
_bs_3 | .18503645 .0009657 .06374241 .0658211 .3042314 (P)
| .0620927 .3027444 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
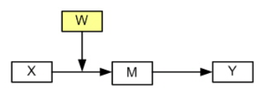
In Model 2 the path between the independent variable and the mediator variable is moderated by W.
Formulas:
m = a0 + a1x + a2w + a3xw y = b0 + b1m + b2x + b3w + b4xw conditional indirect effect = b1(a1 + a3w)
quietly summarize w
global m=r(mean)
global s=r(sd)
generate wx=w*x /* moderator 1 by iv interaction */
sem (m <- x w wx)(y <- m x w wx)
Endogenous variables
Observed: m y
Exogenous variables
Observed: x w wx
Fitting target model:
Iteration 0: log likelihood = -3919.1644
Iteration 1: log likelihood = -3919.1644
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -3919.1644
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
m <- |
x | .2707428 .3780083 0.72 0.474 -.4701398 1.011625
w | .1041694 .3417056 0.30 0.760 -.5655613 .7739002
wx | .0044859 .0066954 0.67 0.503 -.0086368 .0176087
_cons | 19.7711 18.53835 1.07 0.286 -16.56341 56.1056
-----------+----------------------------------------------------------------
y <- | m | .3057916 .0677692 4.51 0.000 .1729665 .4386168 x | .7902703 .3627478 2.18 0.029 .0792976 1.501243 w | .6316515 .3275671 1.93 0.054 -.0103682 1.273671 wx | -.008533 .0064241 -1.33 0.184 -.021124 .0040579 _cons | -14.88752 17.81763 -0.84 0.403 -49.80943 20.03438 -------------+---------------------------------------------------------------- var(e.m)| 52.63581 5.263581 43.26744 64.03265 var(e.y)| 48.3477 4.83477 39.74254 58.81607 ------------------------------------------------------------------------------ LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
nlcom (_b[m:x]+($m-$s)*_b[m:wx])*_b[y:m] /* mean - 1 sd */
_nl_1: (_b[m:x]+(52.775-9.47858602138653)*_b[m:wx])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1421829 .0455118 3.12 0.002 .0529814 .2313843
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m)*_b[m:wx])*_b[y:m] /* mean */
_nl_1: (_b[m:x]+(52.775)*_b[m:wx])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1551852 .0408543 3.80 0.000 .0751121 .2352582
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m+$s)*_b[m:wx])*_b[y:m] /* mean + 1 sd */
_nl_1: (_b[m:x]+(52.775+9.47858602138653)*_b[m:wx])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1681874 .0451294 3.73 0.000 .0797355 .2566394
------------------------------------------------------------------------------
In this example the conditional indirect effects increase slowly as the value of the moderator variable increases.
Bootstrap code for model 2. The example bootstrap command below uses 500 replications. You will probably want to use at least 1,000 or even 5,000 in real research situations.
capture program drop bootm2
program bootm2, rclass
sem (m <- x w wx)(y <- m x w wx)
return scalar cielw = (_b[m:x]+($m-$s)*_b[m:wx])*_b[y:m]
return scalar ciemn = (_b[m:x]+($m)*_b[m:wx])*_b[y:m]
return scalar ciehi = (_b[m:x]+($m+$s)*_b[m:wx])*_b[y:m]
end
bootstrap r(cielw) r(ciemn) r(ciehi), reps(500) nodots: bootm2
Bootstrap results Number of obs = 200
Replications = 500
command: bootm2
_bs_1: r(cielw)
_bs_2: r(ciemn)
_bs_3: r(ciehi)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .1421829 .047612 2.99 0.003 .048865 .2355007
_bs_2 | .1551852 .0409495 3.79 0.000 .0749256 .2354447
_bs_3 | .1681874 .0423557 3.97 0.000 .0851717 .2512031
------------------------------------------------------------------------------
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 500
command: bootm2
_bs_1: r(cielw)
_bs_2: r(ciemn)
_bs_3: r(ciehi)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .14218287 .0009392 .04761201 .0579299 .2551758 (P)
| .0579299 .2551758 (BC)
_bs_2 | .15518515 .0001497 .0409495 .078383 .242382 (P)
| .078383 .242382 (BC)
_bs_3 | .16818743 -.0006398 .04235573 .0869211 .2532646 (P)
| .089544 .2589626 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
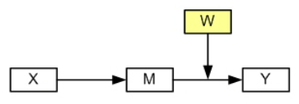
Model 3 (Hayes, 2013 Model 14)
In Model 3 the path between the mediator variable and the dependent variable is moderated by W.
Formulas:
m = a0 + a1x y = b0 + b1m + b2x + b3w + b4mw conditional indirect effect = a1(b1 + b4w)
quietly summarize w
global m=r(mean)
global s=r(sd)
generate mw=m*w /* mv by moderator 1 interaction */
sem (m <- x)(y <- m x w mw)
Endogenous variables
Observed: m y
Exogenous variables
Observed: x w mw
Fitting target model:
Iteration 0: log likelihood = -4260.6166
Iteration 1: log likelihood = -4260.6166
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -4260.6166
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
m <- |
x | .724807 .0579824 12.50 0.000 .6111636 .8384504
_cons | 14.07254 3.100201 4.54 0.000 7.996255 20.14882
-----------+----------------------------------------------------------------
y <- | m | .8193599 .3169173 2.59 0.010 .1982135 1.440506 x | .33696 .0761398 4.43 0.000 .1877287 .4861913 w | .6739726 .2880423 2.34 0.019 .1094201 1.238525 mw | -.0095993 .00574 -1.67 0.094 -.0208495 .0016509 _cons | -17.23954 15.65376 -1.10 0.271 -47.92034 13.44126 -------------+---------------------------------------------------------------- var(e.m)| 58.71925 5.871925 48.26811 71.43329 var(e.y)| 48.10157 4.810157 39.54022 58.51664 ------------------------------------------------------------------------------ LR test of model vs. saturated: chi2(2) = 639.91, Prob > chi2 = 0.0000
nlcom _b[m:x]*(_b[y:m]+($m-$s)*_b[y:mw]) /* mean - 1 sd */
_nl_1: _b[m:x]*(_b[y:m]+(52.775-9.47858602138653)*_b[y:mw])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .2926372 .0700399 4.18 0.000 .1553616 .4299129
------------------------------------------------------------------------------
nlcom _b[m:x]*(_b[y:m]+($m)*_b[y:mw]) /* mean */
_nl_1: _b[m:x]*(_b[y:m]+(52.775)*_b[y:mw])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .2266887 .0524176 4.32 0.000 .1239522 .3294253
------------------------------------------------------------------------------
nlcom _b[m:x]*(_b[y:m]+($m+$s)*_b[y:mw]) /* mean + 1 sd */
_nl_1: _b[m:x]*(_b[y:m]+(52.775+9.47858602138653)*_b[y:mw])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1607402 .0612818 2.62 0.009 .04063 .2808504
------------------------------------------------------------------------------
In this example, the conditional indirect effects decreases as the value of the moderator variable increases.
Bootstrap code for model 3. The example bootstrap command below uses 500 replications. You will probably want to use at least 1,000 or even 5,000 in real research situations.
capture program drop bootm3
program bootm3, rclass
sem (m <- x)(y <- m x w mw)
return scalar cielw = _b[m:x]*(_b[y:m]+($m-$s)*_b[y:mw])
return scalar ciemn = _b[m:x]*(_b[y:m]+($m)*_b[y:mw])
return scalar ciehi = _b[m:x]*(_b[y:m]+($m+$s)*_b[y:mw])
end
bootstrap r(cielw) r(ciemn) r(ciehi), reps(500) nodots: bootm3
Bootstrap results Number of obs = 200
Replications = 500
command: bootm3
_bs_1: r(cielw)
_bs_2: r(ciemn)
_bs_3: r(ciehi)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .2926372 .0666315 4.39 0.000 .1620418 .4232326
_bs_2 | .2266887 .0531356 4.27 0.000 .1225448 .3308326
_bs_3 | .1607402 .0615717 2.61 0.009 .0400619 .2814185
------------------------------------------------------------------------------
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 500
command: bootm3
_bs_1: r(cielw)
_bs_2: r(ciemn)
_bs_3: r(ciehi)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .29263724 -.0008677 .06663153 .1549403 .4144395 (P)
| .1554288 .4178429 (BC)
_bs_2 | .22668872 .0000859 .05313561 .1177044 .3335583 (P)
| .1170573 .3309805 (BC)
_bs_3 | .1607402 .0010394 .06157172 .0423122 .2809089 (P)
| .0423122 .2809089 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
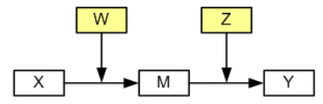
Model 4 (Hayes, 2013 Model 22)
Model 4 has two different moderator variables. One that moderates the path between the independent variable and mediator variable and one that moderates the path between the mediator variable and the dependent variable.
Formulas:
m = a0 + a1x + a2w + a3xw y = b0 + b1m + b2x + b3w + b4xw + b5z + b6mz conditional indirect effect = (b1 + b6z)(a1 + a3w)
quietly summarize w
global m1=r(mean)
global s1=r(sd)
quietly summarize z
global m2=r(mean)
global s2=r(sd)
capture generate wx=w*x /* moderator 1 by iv interaction */
gen mz=m*z /* mv by moderator 2 interaction */
sem (m <- x w wx)(y <- m x w wx z mz)
Endogenous variables
Observed: m y
Exogenous variables
Observed: x w wx z mz
Fitting target model:
Iteration 0: log likelihood = -6096.1477
Iteration 1: log likelihood = -6096.1477
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -6096.1477
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
m <- |
x | .2707428 .3780083 0.72 0.474 -.4701398 1.011625
w | .1041694 .3417056 0.30 0.760 -.5655613 .7739002
wx | .0044859 .0066954 0.67 0.503 -.0086368 .0176087
_cons | 19.7711 18.53835 1.07 0.286 -16.56341 56.1056
-----------+----------------------------------------------------------------
y <- | m | .4013056 .282893 1.42 0.156 -.1531546 .9557658 x | .7571766 .3864076 1.96 0.050 -.0001684 1.514522 w | .6031543 .3562554 1.69 0.090 -.0950935 1.301402 wx | -.0078215 .0069183 -1.13 0.258 -.021381 .0057381 z | .0553245 .2661857 0.21 0.835 -.4663899 .5770389 mz | -.0015944 .0050813 -0.31 0.754 -.0115536 .0083647 _cons | -17.0724 19.0314 -0.90 0.370 -54.37327 20.22847 -------------+---------------------------------------------------------------- var(e.m)| 52.63581 5.263581 43.26744 64.03265 var(e.y)| 48.28407 4.828407 39.69024 58.73866 ------------------------------------------------------------------------------ LR test of model vs. saturated: chi2(2) = 571.85, Prob > chi2 = 0.0000
nlcom (_b[m:x]+($m1-$s1)*_b[m:wx])*(_b[y:m]+($m2-$s2)*_b[y:mz]) /* mean1 - 1 sd1; mean2 - 1 sd2 */
_nl_1: (_b[m:x]+(52.775-9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.405-10.7357934642267)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1557016 .0568792 2.74 0.006 .0442203 .2671828
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1)*_b[m:wx])*(_b[y:m]+($m2-$s2)*_b[y:mz]) /* mean1; mean2 - 1 sd2 */
_nl_1: (_b[m:x]+(52.775)*_b[m:wx])*(_b[y:m]+(52.405-10.7357934642267)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1699401 .0538198 3.16 0.002 .0644552 .275425
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1+$s1)*_b[m:wx])*(_b[y:m]+($m2-$s2)*_b[y:mz]) /* mean1 + 1 sd1; mean2 - 1 sd2 */
_nl_1: (_b[m:x]+(52.775+9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.405-10.7357934642267)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1841786 .059107 3.12 0.002 .068331 .3000263
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1-$s1)*_b[m:wx])*(_b[y:m]+($m2)*_b[y:mz]) /* mean1 - 1 sd1; mean2 */
_nl_1: (_b[m:x]+(52.775-9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.405)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1477424 .04785 3.09 0.002 .0539581 .2415267
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1)*_b[m:wx])*(_b[y:m]+($m2)*_b[y:mz]) /* mean1; mean2 */
_nl_1: (_b[m:x]+(52.775)*_b[m:wx])*(_b[y:m]+(52.405)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1612531 .0431911 3.73 0.000 .0766001 .2459061
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1+$s1)*_b[m:wx])*(_b[y:m]+($m2)*_b[y:mz]) /* mean1 + 1 sd1; mean2 */
_nl_1: (_b[m:x]+(52.775+9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.405)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1747638 .0476804 3.67 0.000 .081312 .2682156
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1-$s1)*_b[m:wx])*(_b[y:m]+($m2+$s2)*_b[y:mz]) /* mean1 - 1 sd1; mean2 + 1 sd */
_nl_1: (_b[m:x]+(52.775-9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.405+10.73579
> 34642267)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1397833 .0513566 2.72 0.006 .0391261 .2404404
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1)*_b[m:wx])*(_b[y:m]+($m2+$s2)*_b[y:mz]) /* mean1; mean2 + 1 sd */
_nl_1: (_b[m:x]+(52.775)*_b[m:wx])*(_b[y:m]+(52.405+10.7357934642267)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1525661 .0486854 3.13 0.002 .0571445 .2479878
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m1+$s1)*_b[m:wx])*(_b[y:m]+($m2+$s2)*_b[y:mz]) /* mean1 + 1 sd1; mean2 + 1 sd */
_nl_1: (_b[m:x]+(52.775+9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.405+10.7357934642267)*_b[y:mz])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .165349 .0534577 3.09 0.002 .0605738 .2701241
------------------------------------------------------------------------------
Bootstrap code for model 4. The example bootstrap command below uses 500 replications. You will probably want to use at least 1,000 or even 5,000 in real research situations.
capture program drop bootm4
program bootm4, rclass
sem (m <- x w wx)(y <- m x w wx z mz)
return scalar ciell = (_b[m:x]+($m1-$s1)*_b[m:wx])*(_b[y:m]+($m2-$s2)*_b[y:mz])
return scalar cieml = (_b[m:x]+($m1)*_b[m:wx])*(_b[y:m]+($m2-$s2)*_b[y:mz])
return scalar ciehl = (_b[m:x]+($m1+$s1)*_b[m:wx])*(_b[y:m]+($m2-$s2)*_b[y:mz])
return scalar cielm = (_b[m:x]+($m1-$s1)*_b[m:wx])*(_b[y:m]+($m2)*_b[y:mz])
return scalar ciemm = (_b[m:x]+($m1)*_b[m:wx])*(_b[y:m]+($m2)*_b[y:mz])
return scalar ciehm = (_b[m:x]+($m1+$s1)*_b[m:wx])*(_b[y:m]+($m2)*_b[y:mz])
return scalar cielh = (_b[m:x]+($m1-$s1)*_b[m:wx])*(_b[y:m]+($m2+$s2)*_b[y:mz])
return scalar ciemh = (_b[m:x]+($m1)*_b[m:wx])*(_b[y:m]+($m2+$s2)*_b[y:mz])
return scalar ciehh = (_b[m:x]+($m1+$s1)*_b[m:wx])*(_b[y:m]+($m2+$s2)*_b[y:mz])
end
bootstrap r(ciell) r(cieml) r(ciehl) r(cielm) r(ciemm) r(ciehm) ///
r(cielh) r(ciemh) r(ciehh), reps(500) nodots: bootm4
Bootstrap results Number of obs = 200
Replications = 500
command: bootm4
_bs_1: r(ciell)
_bs_2: r(cieml)
_bs_3: r(ciehl)
_bs_4: r(cielm)
_bs_5: r(ciemm)
_bs_6: r(ciehm)
_bs_7: r(cielh)
_bs_8: r(ciemh)
_bs_9: r(ciehh)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .1557016 .0649863 2.40 0.017 .0283307 .2830725
_bs_2 | .1699401 .0621157 2.74 0.006 .0481956 .2916846
_bs_3 | .1841786 .0671694 2.74 0.006 .052529 .3158283
_bs_4 | .1477424 .0487353 3.03 0.002 .0522231 .2432618
_bs_5 | .1612531 .0445524 3.62 0.000 .0739321 .2485741
_bs_6 | .1747638 .0493391 3.54 0.000 .078061 .2714666
_bs_7 | .1397833 .0492498 2.84 0.005 .0432554 .2363111
_bs_8 | .1525661 .0472475 3.23 0.001 .0599627 .2451695
_bs_9 | .165349 .0528395 3.13 0.002 .0617855 .2689124
------------------------------------------------------------------------------
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 500
command: bootm4
_bs_1: r(ciell)
_bs_2: r(cieml)
_bs_3: r(ciehl)
_bs_4: r(cielm)
_bs_5: r(ciemm)
_bs_6: r(ciehm)
_bs_7: r(cielh)
_bs_8: r(ciemh)
_bs_9: r(ciehh)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .15570156 -.0011114 .06498635 .0403215 .2988805 (P)
| .0505215 .3103726 (BC)
_bs_2 | .16994009 -.0011208 .06211569 .0493589 .2907081 (P)
| .0592202 .3041216 (BC)
_bs_3 | .18417863 -.0011303 .06716942 .056527 .3229917 (P)
| .0683613 .3390853 (BC)
_bs_4 | .14774241 -.0025282 .04873525 .0589332 .2458749 (P)
| .0740234 .2873931 (BC)
_bs_5 | .1612531 -.002414 .04455236 .0787119 .2513106 (P)
| .0928683 .2640307 (BC)
_bs_6 | .17476379 -.0022999 .04933908 .0872108 .2716488 (P)
| .0949407 .2876344 (BC)
_bs_7 | .13978326 -.0039449 .04924982 .0522442 .2376913 (P)
| .0635381 .2752829 (BC)
_bs_8 | .15256611 -.0037072 .04724748 .0625553 .2519639 (P)
| .0673052 .2589675 (BC)
_bs_9 | .16534895 -.0034695 .05283947 .0625117 .2702666 (P)
| .0756997 .2865739 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
Model 5 (Hayes, 2013 Model 59)
Model 5 has a single moderator variable that moderates both the path between the independent variable and mediator variable and the path between the mediator variable and the dependent variable.
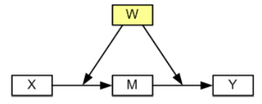
Formulas:
m = a0 + a1x + a2w + a3xw y = b0 + b1m + b2x + b3w + b4xw + b5mw conditional indirect effect = (b1 + b5w)(a1 + a3w)
quietly summarize w
global m=r(mean)
global s=r(sd)
capture generate wx=w*x /* moderator 1 by iv interaction */
capture generate mw=m*w /* mv by moderator 1 interaction */
sem (m <- x w wx)(y <- m x w wx mw)
Endogenous variables
Observed: m y
Exogenous variables
Observed: x w wx mw
Fitting target model:
Iteration 0: log likelihood = -5398.1882
Iteration 1: log likelihood = -5398.1882
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -5398.1882
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
m <- |
x | .2707428 .3780083 0.72 0.474 -.4701398 1.011625
w | .1041694 .3417056 0.30 0.760 -.5655613 .7739002
wx | .0044859 .0066954 0.67 0.503 -.0086368 .0176087
_cons | 19.7711 18.53835 1.07 0.286 -16.56341 56.1056
-----------+----------------------------------------------------------------
y <- | m | .7237774 .3852893 1.88 0.060 -.0313758 1.478931 x | .5236584 .4351217 1.20 0.229 -.3291644 1.376481 w | .7576026 .3460016 2.19 0.029 .079452 1.435753 wx | -.0034416 .0078974 -0.44 0.663 -.0189201 .012037 mw | -.0077956 .0070744 -1.10 0.270 -.0216612 .00607 _cons | -21.81586 18.84366 -1.16 0.247 -58.74876 15.11704 -------------+---------------------------------------------------------------- var(e.m)| 52.63581 5.263581 43.26744 64.03265 var(e.y)| 48.05594 4.805594 39.50271 58.46113 ------------------------------------------------------------------------------ LR test of model vs. saturated: chi2(1) = 696.37, Prob > chi2 = 0.0000
nlcom (_b[m:x]+($m-$s)*_b[m:wx])*(_b[y:m]+($m-$s)*_b[y:mw]) /* mean - 1 sd */
_nl_1: (_b[m:x]+(52.775-9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.775-9.47858602138653)*_b[y:mw])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1795967 .0621316 2.89 0.004 .057821 .3013723
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m)*_b[m:wx])*(_b[y:m]+($m)*_b[y:mw]) /* mean */
_nl_1: (_b[m:x]+(52.775)*_b[m:wx])*(_b[y:m]+(52.775)*_b[y:mw])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1585216 .0411369 3.85 0.000 .0778949 .2391484
------------------------------------------------------------------------------
nlcom (_b[m:x]+($m+$s)*_b[m:wx])*(_b[y:m]+($m+$s)*_b[y:mw]) /* mean + 1 sd */
_nl_1: (_b[m:x]+(52.775+9.47858602138653)*_b[m:wx])*(_b[y:m]+(52.775+9.47858602138653)*_b[y:mw])
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1311629 .0538847 2.43 0.015 .0255509 .236775
------------------------------------------------------------------------------
Bootstrap code for model 5. The example bootstrap command below uses 500 replications. You will probably want to use at least 1,000 or even 5,000 in real research situations.
capture program drop bootm5
program bootm5, rclass
sem (m <- x w wx)(y <- m x w wx mw) return scalar cielw = (_b[m:x]+($m-$s)*_b[m:wx])*(_b[y:m]+($m-$s)*_b[y:mw]) return scalar ciemn = (_b[m:x]+($m)*_b[m:wx])*(_b[y:m]+($m)*_b[y:mw]) return scalar ciehi = (_b[m:x]+($m+$s)*_b[m:wx])*(_b[y:m]+($m+$s)*_b[y:mw]) end bootstrap r(cielw) r(ciemn) r(ciehi), reps(500) nodots: bootm5 Bootstrap results Number of obs = 200 Replications = 500 command: bootm5 _bs_1: r(cielw) _bs_2: r(ciemn) _bs_3: r(ciehi) ------------------------------------------------------------------------------ | Observed Bootstrap Normal-based | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .1795967 .0731346 2.46 0.014 .0362555 .3229378
_bs_2 | .1585216 .0431536 3.67 0.000 .0739422 .2431011
_bs_3 | .1311629 .0501183 2.62 0.009 .0329329 .229393
------------------------------------------------------------------------------
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 500
command: bootm5
_bs_1: r(cielw)
_bs_2: r(ciemn)
_bs_3: r(ciehi)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .17959665 .004129 .07313458 .0583385 .3322092 (P)
| .0600062 .3465318 (BC)
_bs_2 | .15852165 .0022404 .04315356 .0775977 .247842 (P)
| .0758291 .2446393 (BC)
_bs_3 | .13116295 .0023994 .05011829 .0406206 .2343201 (P)
| .0406206 .2343201 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
