This page is just an extension of How can I do moderated mediation in Stata? to include a categorical moderator variable. We will call that page modmed. If you are unfamiliar with moderated mediation you should review the modmed FAQ page before continuing on with this page.
We will to use the same data and the same abbreviated variable names as were used on the modmed page.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear rename science y /* dependent variable */ rename math x /* independent variable */ rename read m /* mediator variable */ rename prog w /* moderator variable with 3 levels */
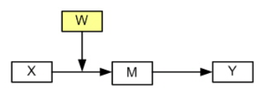
The modmed page presented five different models for moderated mediation. We will select one of them, model 2, to illustrate the use of categorical moderators. The diagram for model 2 looks like this:
Model 2
Using sureg with manual interactions
For our first pass we will manually create indicator variables and interactions.
tab w, gen(w) // create indicator variables generate wx2=w2*x // moderator w2 by iv interaction generate wx3=w3*x // moderator w3 by iv interaction
In model 2 the effect of x on m is what is moderated. So, the interaction terms need to go in the models for both m and y. Thus the sureg command looks like this:
sureg (m x w2 w3 wx2 wx3)(y m x w2 w3 wx2 wx3)
Seemingly unrelated regression
----------------------------------------------------------------------
Equation Obs Parms RMSE "R-sq" chi2 P
----------------------------------------------------------------------
m 200 5 7.493404 0.4632 172.56 0.0000
y 200 6 6.927073 0.5080 206.54 0.0000
----------------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
m |
x | .4896411 .1517936 3.23 0.001 .1921311 .787151
w2 | -12.20637 9.068511 -1.35 0.178 -29.98032 5.567587
w3 | -2.822291 9.952575 -0.28 0.777 -22.32898 16.6844
wx2 | .270153 .1735662 1.56 0.120 -.0700305 .6103366
wx3 | .0222002 .2028633 0.11 0.913 -.3754045 .4198048
_cons | 25.26262 7.67478 3.29 0.001 10.22033 40.30491
-------------+----------------------------------------------------------------
y |
m | .3997664 .0653666 6.12 0.000 .2716503 .5278825
x | .5525436 .1439253 3.84 0.000 .2704552 .8346321
w2 | 5.643216 8.421022 0.67 0.503 -10.86168 22.14812
w3 | -1.079664 9.202235 -0.12 0.907 -19.11571 16.95639
wx2 | -.1860791 .1614174 -1.15 0.249 -.5024513 .1302932
wx3 | -.0157907 .187537 -0.08 0.933 -.3833565 .3517751
_cons | 4.914386 7.284383 0.67 0.500 -9.362742 19.19151
------------------------------------------------------------------------------
Next, we use the nlcom command to compute the conditional indirect effects for each of the levels of the moderator variable. For level one multiply each of the interaction terms, wx2 and wx3 by zero. For level 2, multiply wx2 by one and wx3 by zero. For level 3, just reverse the zeros and ones. Here is the code:
nlcom (_b[m:x]+0*_b[m:wx2]+0*_b[m:wx3])*_b[y:m] // for w = 1
_nl_1: (_b[m:x]+0*_b[m:wx2]+0*_b[m:wx3])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .195742 .0686054 2.85 0.004 .061278 .3302061
------------------------------------------------------------------------------
nlcom (_b[m:x]+1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m] // for w = 2
_nl_1: (_b[m:x]+1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .3037401 .0599894 5.06 0.000 .186163 .4213173
------------------------------------------------------------------------------
nlcom (_b[m:x]+0*_b[m:wx2]+1*_b[m:wx3])*_b[y:m] // for w = 3
_nl_1: (_b[m:x]+0*_b[m:wx2]+1*_b[m:wx3])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .2046169 .0633558 3.23 0.001 .0804418 .3287921
------------------------------------------------------------------------------
From these results we see that the indirect effect is strongest when w = 2 (that is, for the academic program) followed by w = 3 (vocational program) and finally w = 1 (general program). It is also possible to test whether the indirect effects for the three levels differ from one another. We will demonstrate this by looking at the difference between w = 2 and w = 1 (the biggest difference). We do this by subtracting the two nlcom terms.
nlcom ((_b[m:x]+1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m])-((_b[m:x]+0*_b[m:wx2]+0*_b[m:wx3])*_b[y:m])
This simplifies to:
nlcom (1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m] // w1 vs w2
_nl_1: (1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .1079981 .0715978 1.51 0.131 -.0323311 .2483272
------------------------------------------------------------------------------
In this case the difference in the conditional indirect effects is not statistically significant.
In general, nlcom does a reasonably good job of estimating standard errors and confidence intervals using the delta method. However, the delta method has some fairly strong normality assumptions that may not hold for products of coefficients. Many researchers prefer using the bootstrap to obtain confidence intervals.
Bootstrap confidence intervals
To obtain bootstrap confidence intervals for the conditional indirect effects we begin by writing a program, which we have called bootmmcat and saving it as an ado file called bootmmcat.ado. Here is the program:
capture program drop bootmmcat program bootmmcat, rclass sureg (m x w2 w3 wx2 wx3)(y m x w2 w3 wx2 wx3) return scalar w1 = (_b[m:x]+0*_b[m:wx2]+0*_b[m:wx3])*_b[y:m] return scalar w2 = (_b[m:x]+1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m] return scalar w3 = (_b[m:x]+0*_b[m:wx2]+1*_b[m:wx3])*_b[y:m] end
Now we can run bootmmcat using the bootstrap command. We will demonstrate this using 500 bootstrap replications. You will want to use more, say 5,000 or 10,000 or more.
bootstrap r(w1) r(w2) r(w3), reps(500) nodots: bootmmcat
Bootstrap results Number of obs = 200
Replications = 500
command: bootmmcat
_bs_1: r(w1)
_bs_2: r(w2)
_bs_3: r(w3)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .195742 .075913 2.58 0.010 .0469553 .3445288
_bs_2 | .3037401 .0604079 5.03 0.000 .1853429 .4221374
_bs_3 | .2046169 .0729526 2.80 0.005 .0616324 .3476015
------------------------------------------------------------------------------
By default the bootstrap command produces normal-based confidence intervals. To get bias corrected or percentile confidence intervals use the estat boot command.
estat boot, bc percentile
Bootstrap results Number of obs = 200
Replications = 500
command: bootmmcat
_bs_1: r(w1)
_bs_2: r(w2)
_bs_3: r(w3)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | .19574204 .0015209 .07591302 .0623215 .3492891 (P)
| .0633699 .3669358 (BC)
_bs_2 | .30374014 -.0030653 .06040786 .1904437 .4215902 (P)
| .1981149 .4295833 (BC)
_bs_3 | .20461692 .0020635 .07295263 .0732974 .3612065 (P)
| .0818157 .3720523 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
All of the examples above used the manually computed indicators and interactions. The next section shows how to obtain the same results using factor variables.
Using sureg with factor variables
Since this section replicates the above analyses, we will run the commands in a single block of code.
sureg (m c.x##w)(y m c.x##w)
Seemingly unrelated regression
----------------------------------------------------------------------
Equation Obs Parms RMSE "R-sq" chi2 P
----------------------------------------------------------------------
m 200 5 7.493404 0.4632 172.56 0.0000
y 200 6 6.927073 0.5080 206.54 0.0000
----------------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
m |
x | .4896411 .1517936 3.23 0.001 .1921311 .787151
|
w |
2 | -12.20637 9.068511 -1.35 0.178 -29.98032 5.567587
3 | -2.822291 9.952575 -0.28 0.777 -22.32898 16.6844
|
w#c.x |
2 | .270153 .1735662 1.56 0.120 -.0700305 .6103366
3 | .0222002 .2028633 0.11 0.913 -.3754045 .4198048
|
_cons | 25.26262 7.67478 3.29 0.001 10.22033 40.30491
-------------+----------------------------------------------------------------
y |
m | .3997664 .0653666 6.12 0.000 .2716503 .5278825
x | .5525436 .1439253 3.84 0.000 .2704552 .8346321
|
w |
2 | 5.643216 8.421022 0.67 0.503 -10.86168 22.14812
3 | -1.079664 9.202235 -0.12 0.907 -19.11571 16.95639
|
w#c.x |
2 | -.1860791 .1614174 -1.15 0.249 -.5024513 .1302932
3 | -.0157907 .187537 -0.08 0.933 -.3833565 .3517751
|
_cons | 4.914386 7.284383 0.67 0.500 -9.362742 19.19151
------------------------------------------------------------------------------
nlcom (_b[m:x]+0*_b[m:2.w#c.x]+0*_b[m:3.w#c.x])*_b[y:m] // for w = 1
_nl_1: (_b[m:x]+0*_b[m:2.w#c.x]+0*_b[m:3.w#c.x])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .195742 .0686054 2.85 0.004 .061278 .3302061
------------------------------------------------------------------------------
nlcom (_b[m:x]+1*_b[m:2.w#c.x]+0*_b[m:3.w#c.x])*_b[y:m] // for w = 2
_nl_1: (_b[m:x]+1*_b[m:2.w#c.x]+0*_b[m:3.w#c.x])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .3037401 .0599894 5.06 0.000 .186163 .4213173
------------------------------------------------------------------------------
nlcom (_b[m:x]+0*_b[m:2.w#c.x]+1*_b[m:3.w#c.x])*_b[y:m] // for w = 3
_nl_1: (_b[m:x]+0*_b[m:2.w#c.x]+1*_b[m:3.w#c.x])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .2046169 .0633558 3.23 0.001 .0804418 .3287921
------------------------------------------------------------------------------
Using the sureg command is not the only way to compute conditional indirect effects. The next section will show how to do this using the sem command.
Using sem
Since sem does not support factor variables, we will go back to using the manually created indicators and interactions.
sem (m <- x w2 w3 wx2 wx3)(y <- m x w2 w3 wx2 wx3)
Endogenous variables
Observed: m y
Exogenous variables
Observed: x w2 w3 wx2 wx3
Fitting target model:
Iteration 0: log likelihood = -3316.2503
Iteration 1: log likelihood = -3316.2503
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -3316.2503
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
m <- |
x | .4896411 .1517936 3.23 0.001 .1921311 .787151
w2 | -12.20637 9.068511 -1.35 0.178 -29.98032 5.567587
w3 | -2.822291 9.952575 -0.28 0.777 -22.32898 16.6844
wx2 | .270153 .1735662 1.56 0.120 -.0700305 .6103366
wx3 | .0222002 .2028633 0.11 0.913 -.3754045 .4198048
_cons | 25.26262 7.67478 3.29 0.001 10.22033 40.30491
-----------+----------------------------------------------------------------
y <- |
m | .3997664 .0653666 6.12 0.000 .2716503 .5278825
x | .5525436 .1439253 3.84 0.000 .2704552 .8346321
w2 | 5.643216 8.421022 0.67 0.503 -10.86168 22.14812
w3 | -1.079664 9.202235 -0.12 0.907 -19.11571 16.95639
wx2 | -.1860791 .1614174 -1.15 0.249 -.5024513 .1302932
wx3 | -.0157907 .187537 -0.08 0.933 -.3833565 .3517751
_cons | 4.914386 7.284383 0.67 0.500 -9.362742 19.19151
-------------+----------------------------------------------------------------
Variance |
e.m | 56.15111 5.615111 46.15707 68.30909
e.y | 47.98434 4.798434 39.44386 58.37403
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
To see the names of each of the coefficients, just use the coeflegend option with sem.
sem, coeflegend
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -3316.2503
------------------------------------------------------------------------------
| Coef. Legend
-------------+----------------------------------------------------------------
Structural |
m <- |
x | .4896411 _b[m:x]
w2 | -12.20637 _b[m:w2]
w3 | -2.822291 _b[m:w3]
wx2 | .270153 _b[m:wx2]
wx3 | .0222002 _b[m:wx3]
_cons | 25.26262 _b[m:_cons]
-----------+----------------------------------------------------------------
y <- |
m | .3997664 _b[y:m]
x | .5525436 _b[y:x]
w2 | 5.643216 _b[y:w2]
w3 | -1.079664 _b[y:w3]
wx2 | -.1860791 _b[y:wx2]
wx3 | -.0157907 _b[y:wx3]
_cons | 4.914386 _b[y:_cons]
-------------+----------------------------------------------------------------
Variance |
e.m | 56.15111 _b[var(e.m):_cons]
e.y | 47.98434 _b[var(e.y):_cons]
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
As you can see, the names of the coefficients are the same as we used with the sureg command. So, the nlcom commands would be exactly the same.
nlcom (_b[m:x]+0*_b[m:wx2]+0*_b[m:wx3])*_b[y:m] // for w = 1
_nl_1: (_b[m:x]+0*_b[m:wx2]+0*_b[m:wx3])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .195742 .0686054 2.85 0.004 .061278 .3302061
------------------------------------------------------------------------------
nlcom (_b[m:x]+1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m] // for w = 2
_nl_1: (_b[m:x]+1*_b[m:wx2]+0*_b[m:wx3])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .3037401 .0599894 5.06 0.000 .186163 .4213173
------------------------------------------------------------------------------
nlcom (_b[m:x]+0*_b[m:wx2]+1*_b[m:wx3])*_b[y:m] // for w = 3
_nl_1: (_b[m:x]+0*_b[m:wx2]+1*_b[m:wx3])*_b[y:m]
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .2046169 .0633558 3.23 0.001 .0804418 .3287921
------------------------------------------------------------------------------
The methods given on this page can be adapted to any of the other four models for moderated mediation found on the modmed page.