It is not uncommon to believe a variable x predicts a variable y differently over certain ranges of x. In such instances, you may wish to fit a piecewise regression model. The simplest scenario would be fitting two adjoined lines: one line defines the relationship of y and x for x <= c and the other line defines the relationship for x > c. For this scenario, we can use the Stata command nl to find the value of c that yields the best fitting model. The nl command in Stata performs nonlinear least-squares estimation and allows the user to define the function for which it estimates indicated parameters. It is extremely flexible and very useful, though slightly tricky to use at first. The page presents a rather simple example. For details and more examples on nl, see its Stata help page.
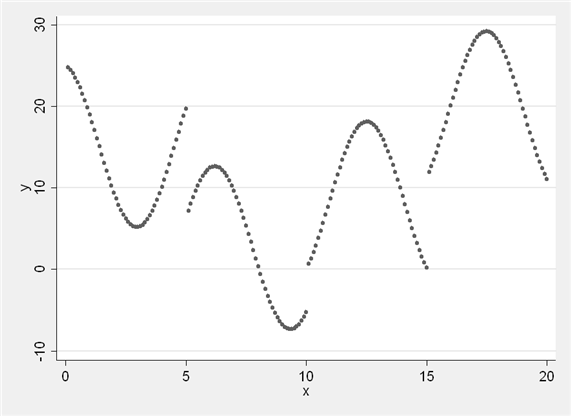
For this example, we will use a fictional dataset where the relationship between x and y is clearly not a single line.
use https://stats.oarc.ucla.edu/wp-content/uploads/2022/07/nl.dta, clear twoway scatter y x
We might look at this plot and believe that there is a downward trend in y as x increases up to a certain point in x. After that point, there is an upward trend in y. Let’s consider the set of parameters we will need to fit. Our first line will involve a slope and an intercept (a1 and b1); our second line will also involve a slope (b2) and we can think of the point at which it meets the first line as its “intercept” defined by the first intercept, the first slope, and the point at which the lines meet (c). We want to estimate four total parameters: two slopes, an intercept, and a cut point. We can indicate these parameters in our nl command and provide starting points for each parameter based on the plot above.
nl (y = ({a1} + {b1}*x)*(x < {c}) + ///
({a1} + {b1}*{c} + {b2}*(x-{c}))*(x >= {c})), ///
initial(a1 25 b1 -2 c 10 b2 2)
Source | SS df MS
-------------+------------------------------ Number of obs = 200
Model | 8770.59791 3 2923.53264 R-squared = 0.5169
Residual | 8197.31882 196 41.8230552 Adj R-squared = 0.5095
-------------+------------------------------ Root MSE = 6.467075
Total | 16967.9167 199 85.2659132 Res. dev. = 1310.224
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
/a1 | 18.53111 1.382652 13.40 0.000 15.80433 21.2579
/b1 | -1.920463 .2668338 -7.20 0.000 -2.446697 -1.394229
/c | 8.987615 .4400011 20.43 0.000 8.11987 9.855359
/b2 | 2.267615 .1915718 11.84 0.000 1.889808 2.645422
------------------------------------------------------------------------------
Parameter a1 taken as constant term in model & ANOVA table
From the output above, we can see estimates of all four parameters. We can use the estimate for the cut point c to generate a new variable, x2, that will allow us to run an ordinary least squares regression of y on x and x2 that effectively fits a piecewise function.
gen x2 = x - 8.987615
replace x2 = 0 if x < 8.987615
regress y x x2
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 2, 197) = 105.39
Model | 8770.59777 2 4385.29889 Prob > F = 0.0000
Residual | 8197.31896 197 41.6107562 R-squared = 0.5169
-------------+------------------------------ Adj R-squared = 0.5120
Total | 16967.9167 199 85.2659132 Root MSE = 6.4506
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | -1.920463 .2023035 -9.49 0.000 -2.319422 -1.521505
x2 | 4.188078 .3214448 13.03 0.000 3.554163 4.821993
_cons | 18.53111 1.275748 14.53 0.000 16.01524 21.04699
------------------------------------------------------------------------------
In the regression output, we can see that we have the same sum of squares we saw in the nl output. We also see that our intercept is unchanged (a1 in the nl output, _cons in the regress output), the coefficient for x matches the first slope from nl, and the coefficient for x2 is equal to (b2 – b1).
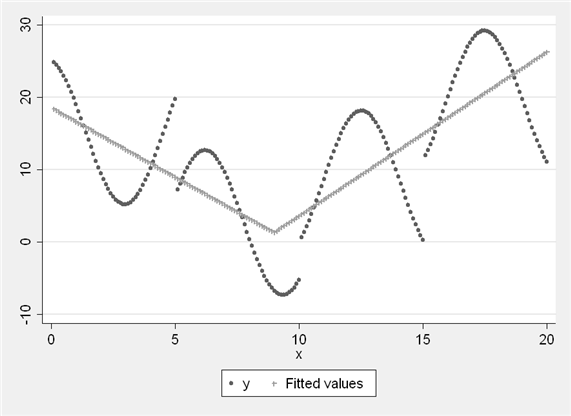
We can plot the predicted values from the regression above.
predict p graph twoway (scatter y x) (scatter p x)
We have found the optimal point to split our piecewise function in this scenario. The same process could be used if we wished to fit quadratic or cubic terms, as long as we carefully described the function and its parameters in our nl command.