NOTE: We are not fully confident that the methods on this page are valid for testing for mediated effects in multilevel models. Proceed at your own risk.
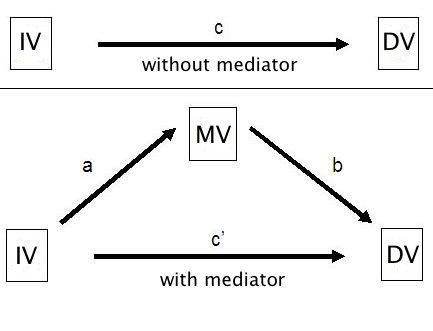
Mediator variables are variables that sit between the independent variable and dependent variable and mediate the effect of the IV on the DV. A model with one mediator is shown in the figure below.
The idea, in mediation analysis, is that some of the effect of the predictor variable, the IV, is transmitted to the DV through the mediator variable, the MV. And some of the effect of the IV passes directly to the DV. That portion of of the effect of the IV that passes through the MV is the indirect effect. The program ml_mediation (see How can I use the search command to search for programs and get additional help? for more information about using search). will compute direct and indirect effects for multilevel data. The approach used in ml_mediation was adapted from Krull & MacKinnon (2001).
When you have multilevel data, the variables may come from different levels of the model. The DV will always be a level one variable. Depending on your data, the IV and MV may be either level 1 or level 2 variables. According to Krull & MacKinnon (2001) a predictor variable may be mediated by a variable at the same level or lower. Thus a level 2 mediator may be mediated by a level 2 or level 1 variable. A level 1 predictor may only be mediated by another level 1 variable. Logically, a level 1 predictor cannot affect a level 2 mediator.
ml_mediation computes the indirect effect as the product of coefficients, i.e., indirect effect = coef[a]*coef[b]. When the response varible is at level 1, ml_mediation uses the xtmixed, reml command by default with xtmixed, mle as an option. When the response variable is at level 2, i.e., the MV is level 2, ml_mediation uses the xtreg, be command. The ml_mediation program will detect which variables are level 1 and which are level 2.
The DV and MV must be a continuous variables. The IV may be a continuous or binary predictor variable. While the CVs may be continuous, binary or factor variables.
We will illustrate the use of the ml_mediation command with a simulated multilevel dataset, ml_med.dta.. Let’s look at the data.
use https://stats.idre.ucla.edu/stat/data/ml_med, clear
summarize, sep(0) /* descriptive statistics */
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
id | 200 100.5 57.87918 1 200
write | 200 52.775 9.478586 31 67
socst | 200 52.405 10.73579 26 71
cid | 200 10.43 5.801152 1 20
abil | 200 156.725 25.75063 104 215
mean_abil | 200 156.725 25.21654 114.0909 205.7
mean_ses | 200 2.055 .3142828 1.444444 2.727273
hon | 200 .545 .4992205 0 1
The variables write, socst, abil and hon are all level 1 variables. The variable cid is the cluster, level 2, identifier, while hon is a binary variable that indicates membership in the honor society. Abil is a composite measure of academic ability. Now, we are ready to try a multilevel mediation model in which all of the variables are at level 1.
ml_mediation, dv(write) iv(hon) mv(abil) l2id(cid)
Equation 1 (c_path): write = hon
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log restricted-likelihood = -628.62552
Iteration 1: log restricted-likelihood = -628.62552
Computing standard errors:
Mixed-effects REML regression Number of obs = 200
Group variable: cid Number of groups = 20
Obs per group: min = 7
avg = 10.0
max = 12
Wald chi2(1) = 32.80
Log restricted-likelihood = -628.62552 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
write | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hon | 4.138289 .7225934 5.73 0.000 2.722032 5.554546
_cons | 50.64367 1.84665 27.42 0.000 47.0243 54.26304
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
cid: Identity |
sd(_cons) | 7.91701 1.331807 5.693395 11.00908
-----------------------------+------------------------------------------------
sd(Residual) | 4.823492 .2549056 4.34889 5.349889
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 191.99 Prob >= chibar2 = 0.0000
Equation 2 (a_path): abil = hon
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log restricted-likelihood = -659.69204
Iteration 1: log restricted-likelihood = -659.69204
Computing standard errors:
Mixed-effects REML regression Number of obs = 200
Group variable: cid Number of groups = 20
Obs per group: min = 7
avg = 10.0
max = 12
Wald chi2(1) = 31.36
Log restricted-likelihood = -659.69204 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
abil | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hon | -4.265397 .7616216 -5.60 0.000 -5.758148 -2.772647
_cons | 159.3095 5.751541 27.70 0.000 148.0367 170.5823
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
cid: Identity |
sd(_cons) | 25.60223 4.169551 18.60596 35.22926
-----------------------------+------------------------------------------------
sd(Residual) | 5.074532 .2681952 4.575188 5.628375
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 537.80 Prob >= chibar2 = 0.0000
Equation 3 (b_path & c_prime): write = abil hon
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log restricted-likelihood = -528.74216
Iteration 1: log restricted-likelihood = -528.74216
Computing standard errors:
Mixed-effects REML regression Number of obs = 200
Group variable: cid Number of groups = 20
Obs per group: min = 7
avg = 10.0
max = 12
Wald chi2(2) = 665.58
Log restricted-likelihood = -528.74216 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
write | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
abil | -.8056925 .0348556 -23.12 0.000 -.8740083 -.7373768
hon | .671848 .3882241 1.73 0.084 -.0890572 1.432753
_cons | 179.0213 8.446553 21.19 0.000 162.4664 195.5763
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
cid: Identity |
sd(_cons) | 28.44004 4.705583 20.56333 39.33388
-----------------------------+------------------------------------------------
sd(Residual) | 2.38897 .1268631 2.152825 2.651018
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 247.90 Prob >= chibar2 = 0.0000
The mediator, abil, is a level 1 variable
c_path = 4.1382892
a_path = -4.2653975
b_path = -.80569254
c_prime = .67184798 same as dir_eff
ind_eff = 3.4365989
dir_eff = .67184798
tot_eff = 4.1084469
proportion of total effect mediated = .83647154
ratio of indirect to direct effect = 5.1151437
ratio of total to direct effect = 6.1151437
The output includes the results of three equations: 1) the DV on the IV, 2) the MV on the IV, and 3) the DV on the MV and IV. The direct, indirect and total effects along with various proportions and ratios are shown below the results of the three equations.
We see that hon is significant in equation 1 and is also a significant predictor of the mediator variable, abil, in equation 2. However, hon is not significant in equation 3 when the mediator is included in the model. This suggests that there is mediation. The output includes the indirect, direct and total effects. It does not however include standard errors or confidence intervals. To get these you need to bootstrap the results. You can bootstrap any of the effects found in the return list.
return list
scalars:
r(tot_eff) = 4.108446903443488
r(dir_eff) = .6718479771360948
r(ind_eff) = 3.436598926307393
r(b_path) = -.8056925398919483
r(a_path) = -4.265397476273364
r(c_path) = 4.13828918116252
We will illustrate this by bootstrapping the ml_mediation command with 500 replications. You may want to do more than 500 reps, maybe a lot more. You will probably also want to use a differnt seed value. Please note that we are bootstrapping cluster so we need the cluster option. We also need to give the clusters a new id when they are resampled, thus the idcluster option. Note that we now have to use the new cluster name, ncid, in the ml_mediation command.
bootstrap indeff=r(ind_eff) direff=r(dir_eff) toteff=r(tot_eff), ///
reps(500) seed(1) cluster(cid) idcluster(ncid): ///
ml_mediation, dv(write) iv(hon) mv(abil) l2id(ncid)
Bootstrap results Number of obs = 200
Replications = 500
command: ml_mediation, dv(write) iv(hon) mv(abil) l2id(ncid)
indeff: r(ind_eff)
direff: r(dir_eff)
toteff: r(tot_eff)
(Replications based on 20 clusters in cid)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
indeff | 3.436599 .7181118 4.79 0.000 2.029126 4.844072
direff | .671848 .3500109 1.92 0.055 -.0141608 1.357857
toteff | 4.108447 .7714546 5.33 0.000 2.596424 5.62047
------------------------------------------------------------------------------
If you have concerns about the normal based confidence confidence intervals, you can obtain percentile or bc confidence intervals with the estat boot command.
estat boot, percentile bc
Bootstrap results Number of obs = 200
Replications = 500
command: ml_mediation, dv(write) iv(hon) mv(abil) l2id(ncid)
indeff: r(ind_eff)
direff: r(dir_eff)
toteff: r(tot_eff)
(Replications based on 20 clusters in cid)
------------------------------------------------------------------------------
| Observed Bootstrap
| Coef. Bias Std. Err. [95% Conf. Interval]
-------------+----------------------------------------------------------------
indeff | 3.4365989 .0173307 .71811179 2.092823 5.00083 (P)
| 2.18301 5.032196 (BC)
direff | .67184798 -.0004241 .35001093 .0312456 1.423976 (P)
| .0567802 1.446936 (BC)
toteff | 4.1084469 .0169066 .77145463 2.610976 5.739329 (P)
| 2.601489 5.61782 (BC)
------------------------------------------------------------------------------
(P) percentile confidence interval
(BC) bias-corrected confidence interval
Based on the confidence intervals it appears that the direct, indirect and total effects are statistically significant at the alpha equal .05 level.
References
Krull,J.L. & MacKinnon,D.P. (2001) Multilevel modeling of individual and group level mediated effects. Multivariate Behavioral Research, 36(2), 249-277.