Attention
See this FAQ by Bauer that discusses the need to decompose within- and between-group effects when using this approach to ensure valid results (https://dbauer.web.unc.edu/wp-content/uploads/sites/7494/2015/08/Centering-in-111-Mediation.pdf).
FAQ starts here
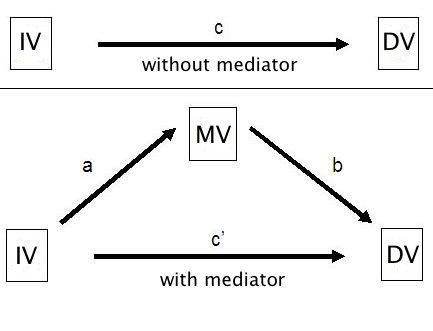
Mediator variables are variables that sit between the independent variable and dependent variable and mediate the effect of the IV on the DV. A model with one mediator is shown in the figure below.
The idea, in mediation analysis, is that some of the effect of the predictor variable, the IV, is transmitted to the DV through the mediator variable, the MV. And some of the effect of the IV passes directly to the DV. That portion of of the effect of the IV that passes through the MV is the indirect effect.
The FAQ page How can I perform mediation with multilevel data? (Method 1) showed how to do multilevel mediation using an approach suggested by Krull & MacKinnon (2001). This page will demonstrate an alternative approach given in the 2006 paper by Bauer, Preacher & Gil. This approach combines the dependent variable and the mediator into a single stacked response variable and runs one mixed model with indicator variables for the DV and mediator to obtain all of the values needed for the analysis.
We will begin by loading in a synthetic data set and reconfiguring it for our analysis. All of the variables in this example (id the cluster ID, x the predictor variable, m the mediator variable, and y the dependent variable) are at level 1 Here is how the first 16 observations look in the original dataset.
use https://stats.idre.ucla.edu/stat/data/ml_sim, clear
list in 1/16, sep(8)
+-------------------------------------------+
| id x m y |
|-------------------------------------------|
1. | 1 1.5451205 .10680165 .56777601 |
2. | 1 2.275272 2.1104394 1.2061451 |
3. | 1 .7866992 .03888269 -.26127707 |
4. | 1 -.06185872 .47940645 -.75899036 |
5. | 1 .11725984 .59082413 .51907688 |
6. | 1 1.4809238 .89094498 -.63111928 |
7. | 1 .89275955 -.22767749 .1520794 |
8. | 1 .92460471 .72917853 .23463058 |
|-------------------------------------------|
9. | 2 1.0031088 -.36224011 -1.1507768 |
10. | 2 -1.1914322 -2.9658042 -3.7168343 |
11. | 2 -1.8003534 -3.6484285 -4.4695533 |
12. | 2 -1.2585149 -2.3043152 -3.2232902 |
13. | 2 -.47077056 -1.4640601 -2.6614767 |
14. | 2 -2.8150223 -2.1196492 -2.1692942 |
15. | 2 -.26598751 -.36127735 -2.1726739 |
16. | 2 -1.5617038 -2.5556008 -3.857205 |
+-------------------------------------------+
Let’s look at our data.
summarize x m y
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
x | 800 -.1539876 1.330374 -4.151426 3.869661
m | 800 -.0247739 1.483614 -6.47837 5.012422
y | 800 -.1833981 1.66918 -8.600032 5.919008
corr x m y
(obs=800)
| x m y
-------------+---------------------------
x | 1.0000
m | 0.5404 1.0000
y | 0.5537 0.7591 1.0000
tab id
id | Freq. Percent Cum.
------------+-----------------------------------
1 | 8 1.00 1.00
2 | 8 1.00 2.00
3 | 8 1.00 3.00
[output omitted]
98 | 8 1.00 98.00
99 | 8 1.00 99.00
100 | 8 1.00 100.00
------------+-----------------------------------
Total | 800 100.00
So there are 100 level-2 units each with eight observations. Let’s look at the three models of a mediation analysis beginning with the model with just the IV.
xtmixed y x || id: x, var cov(un)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -1214.1953
Iteration 1: log likelihood = -1214.1952
Computing standard errors:
Mixed-effects ML regression Number of obs = 800
Group variable: id Number of groups = 100
Obs per group: min = 8
avg = 8.0
max = 8
Wald chi2(1) = 139.83
Log likelihood = -1214.1952 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .6897692 .0583307 11.83 0.000 .575443 .8040953
_cons | -.0273891 .0954593 -0.29 0.774 -.214486 .1597077
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Unstructured |
var(x) | .2138149 .0465543 .1395419 .3276209
var(_cons) | .737622 .1272275 .5260364 1.034313
cov(x,_cons) | -.0262811 .0559555 -.1359518 .0833896
-----------------------------+------------------------------------------------
var(Residual) | .822606 .0470298 .735406 .9201455
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 367.76 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference.
Next, comes the model with the mediator predicted by the IV.
xtmixed m x || id: x, var cov(un)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -1113.6567
Iteration 1: log likelihood = -1113.6567
Computing standard errors:
Mixed-effects ML regression Number of obs = 800
Group variable: id Number of groups = 100
Obs per group: min = 8
avg = 8.0
max = 8
Wald chi2(1) = 175.20
Log likelihood = -1113.6567 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
m | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .6114761 .0461973 13.24 0.000 .5209311 .7020212
_cons | .094974 .0911449 1.04 0.297 -.0836668 .2736148
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Unstructured |
var(x) | .1147085 .0284269 .0705751 .1864401
var(_cons) | .7010477 .1165732 .5060648 .9711559
cov(x,_cons) | .0065896 .0412717 -.0743015 .0874806
-----------------------------+------------------------------------------------
var(Residual) | .6449282 .0365222 .5771756 .7206342
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(3) = 396.83 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference.
Finally, the model with both the IV and mediator predicting the DV.
xtmixed y m x || id: m x, var cov(un)
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -1016.1698
Iteration 1: log likelihood = -1016.0624
Iteration 2: log likelihood = -1016.0623
Computing standard errors:
Mixed-effects ML regression Number of obs = 800
Group variable: id Number of groups = 100
Obs per group: min = 8
avg = 8.0
max = 8
Wald chi2(2) = 311.46
Log likelihood = -1016.0623 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
m | .6252951 .04657 13.43 0.000 .5340196 .7165706
x | .2500122 .0384508 6.50 0.000 .1746501 .3253743
_cons | -.0937981 .0616632 -1.52 0.128 -.2146558 .0270596
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Unstructured |
var(m) | .1178902 .0302985 .0712383 .1950931
var(x) | .0376483 .0210683 .012572 .112742
var(_cons) | .2573218 .0525485 .1724447 .3839753
cov(m,x) | -.0018785 .0188857 -.0388937 .0351368
cov(m,_cons) | -.0060299 .0281886 -.0612786 .0492187
cov(x,_cons) | -.0307884 .0242063 -.0782318 .016655
-----------------------------+------------------------------------------------
var(Residual) | .5078589 .0307909 .4509575 .57194
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(6) = 313.19 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference.
We see that the IV although still significant has been reduced from .69 to .25.
Now, we need to restructure the data to stack y on m for each row and create indicator variables for both the mediator and the dependent variables. Here’s how we can do this.
rename y z0 // rename for reshaping
generate z1=m // create z1 for reshaping
gen fid=_n // create temp id for reshaping
reshape long z, i(fid) j(s)
rename s sm // indicator for the mediator
gen sy= ~sm // indicator for the dv
list in 1/16, sep(8)
+----------------------------------------------------------+
| fid sm id x m z sy |
|----------------------------------------------------------|
1. | 1 0 1 1.5451205 .10680165 .567776 1 |
2. | 1 1 1 1.5451205 .10680165 .1068017 0 |
3. | 2 0 1 2.275272 2.1104394 1.206145 1 |
4. | 2 1 1 2.275272 2.1104394 2.110439 0 |
5. | 3 0 1 .7866992 .03888269 -.2612771 1 |
6. | 3 1 1 .7866992 .03888269 .0388827 0 |
7. | 4 0 1 -.06185872 .47940645 -.7589904 1 |
8. | 4 1 1 -.06185872 .47940645 .4794064 0 |
|----------------------------------------------------------|
9. | 5 0 1 .11725984 .59082413 .5190769 1 |
10. | 5 1 1 .11725984 .59082413 .5908241 0 |
11. | 6 0 1 1.4809238 .89094498 -.6311193 1 |
12. | 6 1 1 1.4809238 .89094498 .890945 0 |
13. | 7 0 1 .89275955 -.22767749 .1520794 1 |
14. | 7 1 1 .89275955 -.22767749 -.2276775 0 |
15. | 8 0 1 .92460471 .72917853 .2346306 1 |
16. | 8 1 1 .92460471 .72917853 .7291785 0 |
+----------------------------------------------------------+
The new response variable is called z and has y stacked on m. We named the indicators for the mediator and the DV sm and sy respectively, to be consistent with Bauer et al (2006). We have also created a new m that contains the value for the mediator from each of the original observations.
Next, we are going to create some interactions terms manually. We are doing this manually because we need to use these terms in both the fixed and random parts of our mixed model.
gen smx=sm*x // a gen sym=sy*m // b gen syx=sy*x // cprime
Now we can run our mixed model using xtmixed. Notice that because we include the sm and sy indicators in the model that we need to use the nocons option for both the fixed and random effects.
xtmixed z sm smx sy sym syx, nocons ///
> || id: sm smx sy sym syx, nocons cov(un) ///
> || fid: sm, nocons var reml
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log restricted-likelihood = -2130.2314
Iteration 1: log restricted-likelihood = -2126.1762
Iteration 2: log restricted-likelihood = -2126.1352
Iteration 3: log restricted-likelihood = -2126.1345
Iteration 4: log restricted-likelihood = -2126.1345
Computing standard errors:
Mixed-effects REML regression Number of obs = 1600
-----------------------------------------------------------
| No. of Observations per Group
Group Variable | Groups Minimum Average Maximum
----------------+------------------------------------------
id | 100 16 16.0 16
fid | 800 2 2.0 2
-----------------------------------------------------------
Wald chi2(5) = 342.64
Log restricted-likelihood = -2126.1345 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
z | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sm | .0932149 .0894316 1.04 0.297 -.0820678 .2684976
smx | .6118566 .0464952 13.16 0.000 .5207276 .7029856
sy | -.096852 .0619583 -1.56 0.118 -.218288 .0245839
sym | .6105632 .0455363 13.41 0.000 .5213136 .6998127
syx | .2208116 .0372474 5.93 0.000 .147808 .2938152
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Unstructured |
var(sm) | .6794348 .1131795 .49018 .9417594
var(smx) | .1204833 .0293158 .0747849 .1941063
var(sy) | .2702841 .0540872 .1825932 .400089
var(sym) | .1118722 .0291408 .0671426 .1864
var(syx) | .032437 .020045 .0096611 .1089068
cov(sm,smx) | .018161 .0410871 -.0623682 .0986902
cov(sm,sy) | .0568122 .0645235 -.0696515 .183276
cov(sm,sym) | .0093218 .0390042 -.0671251 .0857687
cov(sm,syx) | -.0066738 .0345052 -.0743028 .0609553
cov(smx,sy) | .0118807 .0292113 -.0453725 .0691338
cov(smx,sym) | .0989554 .0228226 .054224 .1436868
cov(smx,syx) | -.0214964 .0188476 -.0584371 .0154443
cov(sy,sym) | -.0042835 .0278161 -.058802 .050235
cov(sy,syx) | -.0182759 .0233301 -.0640021 .0274502
cov(sym,syx) | .005422 .017884 -.02963 .040474
-----------------------------+------------------------------------------------
fid: Identity |
var(sm) | .1377656 .0477088 .0698822 .2715911
-----------------------------+------------------------------------------------
var(Residual) | .5089653 .0306737 .4522609 .5727793
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(16) = 765.76 Prob > chi2 = 0.0000
Note: LR test is conservative and provided only for reference.
The last random effect || fid: sm, nocons is included to account for the heterogeneity between the DV and the mediator.
We now have access to all of the information needed to compute the average indirect effect and average total effect and their standard errors using the equations given in Bauer, et. al. (2006).
avg_ind_eff = a*b + σaj,bj
se_avg_ind_eff = b2*Var(a) + a2*Var(b) + Var(a)*Var(b) + 2*a*b*Cov(a,b) +
Cov(a,b)2 + Var(σaj,bj)
avg_tot_eff = a*b + σaj,bj + cprime
se_avg_tot_eff = b2*Var(a) + a2*Var(b) + Var(a)*Var(b) + 2*a*b*Cov(a,b) + Cov(a,b)2 +
Var(cprime) + 2*b*Cov(a,c) + 2*a*Cov(b,c) + Var(σaj,bj)
The last term of each standard error above, Var(σaj,bj), is the square of the standard error for the random effect cov(smx, smy), i.e., .0228226^2.
global a = _b[smx] // a path global sa = _se[smx] // se a path global b = _b[sym] // b path global sb = _se[sym] // se b path global c = _b[syx] // cprime path global sc = _se[syx] // se cprime path * covariances of fixed effects parameter estimates mat v=e(V) global covab=v[4,2] // cov(a,b) global covac=v[5,2] // cov(a,c) global covbc=v[5,4] // cov(b.c)
We also need the value for Var(σaj,bj), which we can obtain using the _diparm (display parameter) command. For more information on _diparm see How can I access the random effects after xtmixed? Here is how we use the _diparm command for our example.
_diparm atr1_1_2_4 lns1_1_2 lns1_1_4, f(tanh(@1)*exp(@2+@3)) /// d((1-(tanh(@1)^2))*exp(@2+@3) tanh(@1)*exp(@2+@3) /// tanh(@1)*exp(@2+@3)) global sajbj=r(est) global seajbj=r(se)
We are now ready to compute the values we need and to display the results. Here are the commands.
display dis "a: " _col(30) $a dis "b: " _col(30) $b dis "c prime: " _col(30) $c dis "cov(ajbj): " _col(30) $sajbj dis global avg_ind_eff = $a*$b + $sajbj global avg_tot_eff = $a*$b + $sajbj + $c dis "average indirect effect: " _col(30) $avg_ind_eff global var9 = ($b)^2*($sa)^2 + ($a)^2*($sb)^2 + ($sa)^2*($sb)^2 + /// 2*$a*$b*$covab + ($covab)^2 + ($seajbj)^2 dis "standard error average indirect effect: " _col(30) sqrt($var9) dis "ratio: " _col(30) $avg_ind_eff/sqrt($var9) dis "LCL: " _col(30) $avg_ind_eff-1.96*sqrt($var9) dis "UCL: " _col(30) $avg_ind_eff+1.96*sqrt($var9) dis dis "average total effect: " _col(30) $avg_tot_eff global var10 = $var9 + ($sc)^2 + 2*$b*$covac + 2*$a*$covbc dis "standard error average total effect: " _col(30) sqrt($var10) dis "ratio: " _col(30) $avg_tot_eff/sqrt($var10) dis "LCL: " _col(30) $avg_tot_eff-1.96*sqrt($var10) dis "UCL: " _col(30) $avg_tot_eff+1.96*sqrt($var10)
And here are the results.
a: .61185658 b: .61056318 c prime: .22081162 cov(ajbj): .09895544 average indirect effect: .47253254 standard error average indirect effect: .05333007 Ratio: 8.8605279 LCL: .36800561 UCL: .57705946 average total effect: .69334416 standard error average total effect: .05829333 ratio: 11.894057 LCL: .57908923 UCL: .80759908
References
Bauer,D.J., Preacher,K.J. & Gil,K.M. (2006) Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: New procedures and recommendations. Psychological Methods, 11(2), 142-163.
Krull,J.L. & MacKinnon,D.P. (2001) Multilevel modeling of individual and group level mediated effects. Multivariate Behavioral Research, 36(2), 249-277.