Say that you want to look at the relationship between how much a child talks on the phone and the age of the child. You get a random sample of 200 kids and ask them how old they are and how many minutes they spend talking on the phone. You start with a scatterplot of the data like below.
use https://stats.idre.ucla.edu/stat/stata/faq/talk, clear twoway (scatter talk age) (lfit talk age)
Looking at this you are not happy with the nonlinearity that you see in the data, so try to add a quadratic fit.
twoway (scatter talk age) (lfit talk age) (qfit talk age)
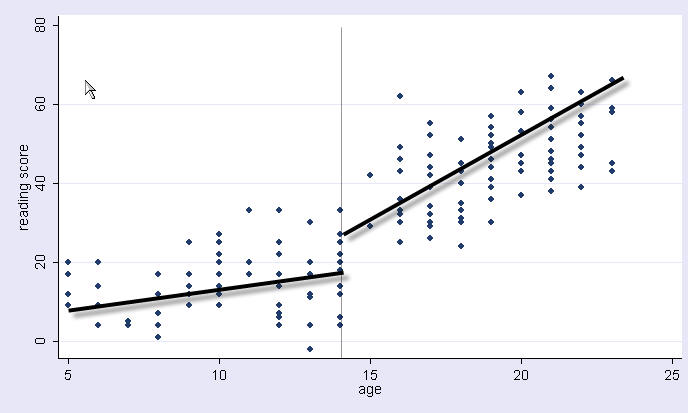
Thinking about this more, you decide that you think that the amount of time that kids talk on the phone changes dramatically at age 14, and that the slope might change at that age as well. You think that a piecewise regression might make more sense, where before age 14 there is an intercept and linear slope, and after age 14, there is a different intercept and different linear slope, kind of like pictured below with just freehand drawing of what the two regression lines might look like.
Try 1: Separate regressions
To investigate this, we can run two separate regressions, one for before age 14, and one for after age 14. We can compare the results of these two models.
* Before age 14
regress talk age if age < 14
Source | SS df MS Number of obs = 62
-------------+------------------------------ F( 1, 60) = 3.19
Model | 175.387138 1 175.387138 Prob > F = 0.0791
Residual | 3297.59673 60 54.9599456 R-squared = 0.0505
-------------+------------------------------ Adj R-squared = 0.0347
Total | 3472.98387 61 56.9341618 Root MSE = 7.4135
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .6820981 .3818309 1.79 0.079 -.0816775 1.445874
_cons | 8.074878 3.980529 2.03 0.047 .1126352 16.03712
------------------------------------------------------------------------------
* At age 14 and after
regress talk age if age >= 14
Source | SS df MS Number of obs = 138
-------------+------------------------------ F( 1, 136) = 144.88
Model | 11570.8699 1 11570.8699 Prob > F = 0.0000
Residual | 10861.5142 136 79.8640747 R-squared = 0.5158
------------+------------------------------ Adj R-squared = 0.5123
Total | 22432.3841 137 163.74003 Root MSE = 8.9367
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | 3.629046 .3014985 12.04 0.000 3.032814 4.225277
_cons | -24.97267 5.709467 -4.37 0.000 -36.26348 -13.68185
------------------------------------------------------------------------------
Note how the slopes do seem quite different for the two groups. However, the intercepts don’t make much sense, since they are the predicted time talking on the phone when one is 0 years old.
Try 2: Separate regression with age centered at 14
Let’s rescale (center) age by subtracting 14. Then, when age is 0, that really refers to being 14 years old.
generate age14 = age - 14
regress talk age14 if age < 14
Source | SS df MS Number of obs = 62
-------------+------------------------------ F( 1, 60) = 3.19
Model | 175.387138 1 175.387138 Prob > F = 0.0791
Residual | 3297.59673 60 54.9599456 R-squared = 0.0505
-------------+------------------------------ Adj R-squared = 0.0347
Total | 3472.98387 61 56.9341618 Root MSE = 7.4135
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age14 | .6820981 .3818309 1.79 0.079 -.0816775 1.445874
_cons | 17.62425 1.752455 10.06 0.000 14.11882 21.12968
------------------------------------------------------------------------------
regress talk age14 if age >= 14
Source | SS df MS Number of obs = 138
-------------+------------------------------ F( 1, 136) = 144.88
Model | 11570.8699 1 11570.8699 Prob > F = 0.0000
Residual | 10861.5142 136 79.8640747 R-squared = 0.5158
-------------+------------------------------ Adj R-squared = 0.5123
Total | 22432.3841 137 163.74003 Root MSE = 8.9367
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age14 | 3.629046 .3014985 12.04 0.000 3.032814 4.225277
_cons | 25.83397 1.626457 15.88 0.000 22.61755 29.05039
------------------------------------------------------------------------------
Note how the slopes for the two groups stayed the same, but now the intercepts (_cons) are the predicted talking time at age 14 for the two groups. We can see that at age 14 there seems to be not only a change in the slope (from .682 to 3.62) but also a jump in the intercept (from 17.6 to 25.8). This suggest that at age 14, there is discontinuous jump in time talking on the phone as well as a change in the slope as well. However, this is merely suggestive, we should really test this in a combined model.
Try 3: Combined model, coding for separate slope and intercept
We now combine the two models into a single model. To do this, we need to create some new variables.
- age1 is the age centered around age 14 but converted to 0s after age 14 (representing the effect of age for before 14 year olds).
- age2 is the age centered around age 14 but converted to 0s before 14 (representing the effect of age for after 14 year olds).
- int1 is 1 before age 14 (representing the intercept for before 14 year olds).
- int2 is 1 after age 14 (representing the intercept for after 14 year olds).
generate age1 = (age - 14) replace age1 = 0 if age >= 14 generate age2 = (age - 14) replace age2 = 0 if age < 14 generate int1 = 1 replace int1 = 0 if age >= 14 generate int2 = 1 replace int2 = 0 if age < 14
That might have been confusing, so let us show what these variables look like in a table below. Note that we have a strange person who is 13.9999 years old (very very close to being 14, but not quite). This person will be helpful for seeing the effect of the jump from going from being under 14 to being 14.
* Check the coding tablist age int1 int2 age1 age2, sort(v) +--------------------------------------------------+ | age int1 int2 age1 age2 Freq | |--------------------------------------------------| | 5 1 0 -9 0 4 | | 6 1 0 -8 0 4 | | 7 1 0 -7 0 2 | | 8 1 0 -6 0 5 | | 9 1 0 -5 0 6 | | 10 1 0 -4 0 13 | | 11 1 0 -3 0 3 | | 12 1 0 -2 0 13 | | 13 1 0 -1 0 11 | | 13.99999 1 0 -9.54e-06 0 1 | |--------------------------------------------------| | 14 0 1 0 0 11 | | 15 0 1 0 1 2 | | 16 0 1 0 2 15 | | 17 0 1 0 3 20 | | 18 0 1 0 4 12 | | 19 0 1 0 5 25 | | 20 0 1 0 6 8 | | 21 0 1 0 7 22 | | 22 0 1 0 8 16 | | 23 0 1 0 9 7 | +--------------------------------------------------+
Now we are ready to run our combined regression. We use the hascons option because our model has an implied constant, int1 plus int2 which adds up to 1. By including this option, the overall test of the model is appropriate and Stata does not try to include its own constant.
* Run the regresion, compare to try 2
regress talk int1 int2 age1 age2, hascons
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 210.66
Model | 45655.2691 3 15218.423 Prob > F = 0.0000
Residual | 14159.1109 196 72.2403617 R-squared = 0.7633
-------------+------------------------------ Adj R-squared = 0.7597
Total | 59814.38 199 300.574774 Root MSE = 8.4994
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
int1 | 17.62425 2.009156 8.77 0.000 13.66191 21.58659
int2 | 25.83397 1.54688 16.70 0.000 22.7833 28.88464
age1 | .6820981 .4377618 1.56 0.121 -.1812301 1.545426
age2 | 3.629046 .2867473 12.66 0.000 3.063539 4.194552
------------------------------------------------------------------------------
Now let’s obtain the predicted values (shown in the table below) and relate those to the meaning of the coefficients above.
- age1 is the slope when age is less than 14. For example, as you go from being age 5 to 6, phone talking goes from 11.48 to 12.17, and that equals .68 (with rounding).
- age2 is the slope when age is 14 or higher. For example, as you go from being age 15 to 16, phone talking goes from 29.46 to 33.09, and that equals 3.62 (with rounding).
- int1 is the predicted mean for someone who is just infinitely close to being 14 years old (but not quite 14). Note that when someone is 13.9999 their predicted mean is the same as int1.
- int2 is the predicted mean for someone who just turned 14 years old, and note that 25.83 is the value for int2 and is the value for the predicted value at exactly age 14.
predict yhat tablist age yhat, sort(v) // get this via search tablist +----------------------------+ | age yhat Freq | |----------------------------| | 5 11.48537 4 | | 6 12.16747 4 | | 7 12.84956 2 | | 8 13.53166 5 | | 9 14.21376 6 | | 10 14.89586 13 | | 11 15.57796 3 | | 12 16.26005 13 | | 13 16.94215 11 | | 13.99999 17.62424 1 | |----------------------------| | 14 25.83397 11 | | 15 29.46302 2 | | 16 33.09206 15 | | 17 36.72111 20 | | 18 40.35015 12 | | 19 43.9792 25 | | 20 47.60825 8 | | 21 51.23729 22 | | 22 54.86634 16 | | 23 58.49538 7 | +----------------------------+
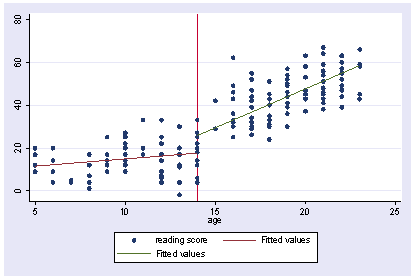
Here we make a graph of the results.
twoway (scatter talk age) /// (line yhat age if age <14, sort) (line yhat age if age >=14, sort), xline(14)
You might want to test whether the difference in the intercepts is 0, so we can do this below. Indeed, as you turn 14 years old, you have a "jump" in the time you talk on the phone, by 8.2 minutes.
lincom int2 - int1
( 1) - int1 + int2 = 0
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 8.20972 2.535655 3.24 0.001 3.209051 13.21039
------------------------------------------------------------------------------
You can also test whether the slopes are different. The slope after 14 is greater by 2.94, and that difference (2.94) is significantly different from 0.
lincom age2 - age1
( 1) - age1 + age2 = 0
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 2.946947 .5233158 5.63 0.000 1.914895 3.979
------------------------------------------------------------------------------
Try 4: Alternate coding, coding to compare intercept and slope
This is another way you can code this model. Note that we include age14 and age2 for the two terms for age, and _cons and int2 to represent the intercept values. With this coding, age2 and int2 represent the change from being less than 14 to being 14 and older.
regress talk age14 age2 int2
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 210.66
Model | 45655.2691 3 15218.423 Prob > F = 0.0000
Residual | 14159.1109 196 72.2403617 R-squared = 0.7633
-------------+------------------------------ Adj R-squared = 0.7597
Total | 59814.38 199 300.574774 Root MSE = 8.4994
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age14 | .6820981 .4377618 1.56 0.121 -.1812301 1.545426
age2 | 2.946947 .5233158 5.63 0.000 1.914895 3.979
int2 | 8.20972 2.535655 3.24 0.001 3.209051 13.21039
_cons | 17.62425 2.009156 8.77 0.000 13.66191 21.58659
------------------------------------------------------------------------------
Using this coding scheme, here is the meaning of the coefficients.
- age14 is the slope when age is less than 14.
- age2 is the change in the slope as a result of becoming age 14 or higher (as compared to being less than 14). Note how this value of 2.94 corresponds to the lincom command above comparing the slope for after 14 to the slope before 14.
- _cons is the predicted mean for someone who is just infinitely close to being 14 years old (but not quite 14).
- int2 is the predicted mean for someone who just turned 14 years old minus the predicted mean for someone who is infinitely close to being 14 years old (the jump that occurs at age 14). Note how this corresponds to the result from the lincom command above that tested the difference in the intercepts.
As you can see, the coefficients for age2 and int2 now focus on the change that results from becoming 14 years old.
Below we compute the predicted values calling them yhat2. Note how the predicted values are the same for this model and the prior model, because the models are essentially the same, they are just parameterized differently.
predict yhat2 (option xb assumed; fitted values) tablist age yhat yhat2, sort(v) +---------------------------------------+ | age yhat yhat2 Freq | |---------------------------------------| | 5 11.48537 11.48537 4 | | 6 12.16747 12.16747 4 | | 7 12.84956 12.84956 2 | | 8 13.53166 13.53166 5 | | 9 14.21376 14.21376 6 | |---------------------------------------| | 10 14.89586 14.89586 13 | | 11 15.57796 15.57796 3 | | 12 16.26005 16.26005 13 | | 13 16.94215 16.94215 11 | | 13.99999 17.62424 17.62424 1 | |---------------------------------------| | 14 25.83397 25.83397 11 | | 15 29.46302 29.46302 2 | | 16 33.09206 33.09206 15 | | 17 36.72111 36.72111 20 | | 18 40.35015 40.35015 12 | |---------------------------------------| | 19 43.9792 43.9792 25 | | 20 47.60825 47.60825 8 | | 21 51.23729 51.23729 22 | | 22 54.86634 54.86634 16 | | 23 58.49538 58.49538 7 | +---------------------------------------+
Try 5: Using mkspline and getting separate slope coding
Stata has a very nice convenience command for these kinds of models called mkspline. Below we use the command to create the variables xage1 (age before 14) and xage2 (age after 14). We then show the coding below.
mkspline xage1 14 xage2 = age tablist age xage1 xage2, sort(v) +------------------------------------+ | age xage1 xage2 Freq | |------------------------------------| | 5 5 0 4 | | 6 6 0 4 | | 7 7 0 2 | | 8 8 0 5 | | 9 9 0 6 | |------------------------------------| | 10 10 0 13 | | 11 11 0 3 | | 12 12 0 13 | | 13 13 0 11 | | 13.99999 13.99999 0 1 | |------------------------------------| | 14 14 0 11 | | 15 14 1 2 | | 16 14 2 15 | | 17 14 3 20 | | 18 14 4 12 | |------------------------------------| | 19 14 5 25 | | 20 14 6 8 | | 21 14 7 22 | | 22 14 8 16 | | 23 14 9 7 | +------------------------------------+
We then run the regression below. Note that the effect for xage1 is the slope before age 14, and xage2 is the slope after age 14. The term int2 corresponds to the jump in the regression lines at age 14. The value for _cons is the predicted amount of talking for someone who is zero years old.
regress talk xage1 xage2 int2
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 210.66
Model | 45655.2691 3 15218.423 Prob > F = 0.0000
Residual | 14159.1109 196 72.2403617 R-squared = 0.7633
-------------+------------------------------ Adj R-squared = 0.7597
Total | 59814.38 199 300.574774 Root MSE = 8.4994
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
xage1 | .6820981 .4377618 1.56 0.121 -.1812301 1.545426
xage2 | 3.629046 .2867473 12.66 0.000 3.063539 4.194552
int2 | 8.20972 2.535655 3.24 0.001 3.209051 13.21039
_cons | 8.074878 4.5636 1.77 0.078 -.9251856 17.07494
------------------------------------------------------------------------------
Try 6: Using mkspline and getting coding to compare slopes
We repeat the same commands from above, but use the marginal option on the mkspline command and this time create variables named yage1 and yage2. The coding is shown below.
mkspline yage1 14 yage2 = age, marginal
tablist age yage1 yage2, sort(v)
+------------------------------------+
| age yage1 yage2 Freq |
|------------------------------------|
| 5 5 0 4 |
| 6 6 0 4 |
| 7 7 0 2 |
| 8 8 0 5 |
| 9 9 0 6 |
|------------------------------------|
| 10 10 0 13 |
| 11 11 0 3 |
| 12 12 0 13 |
| 13 13 0 11 |
| 13.99999 13.99999 0 1 |
|------------------------------------|
| 14 14 0 11 |
| 15 15 1 2 |
| 16 16 2 15 |
| 17 17 3 20 |
| 18 18 4 12 |
|------------------------------------|
| 19 19 5 25 |
| 20 20 6 8 |
| 21 21 7 22 |
| 22 22 8 16 |
| 23 23 9 7 |
+------------------------------------+
regress talk yage1 yage2 int2
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 210.66
Model | 45655.2691 3 15218.423 Prob > F = 0.0000
Residual | 14159.1109 196 72.2403617 R-squared = 0.7633
-------------+------------------------------ Adj R-squared = 0.7597
Total | 59814.38 199 300.574774 Root MSE = 8.4994
------------------------------------------------------------------------------
talk | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yage1 | .6820981 .4377618 1.56 0.121 -.1812301 1.545426
yage2 | 2.946947 .5233158 5.63 0.000 1.914895 3.979
int2 | 8.20972 2.535655 3.24 0.001 3.209051 13.21039
_cons | 8.074878 4.5636 1.77 0.078 -.9251856 17.07494
------------------------------------------------------------------------------
Note that all of the coefficients are the same as the last model, except for yage2. This coefficient now is the change in the slope from after age 14 to before age 14 (i.e., 3.62 – .68 = 2.94). Coded in this fashion, yage2 tests for differences in the slopes.
Summary
This brief FAQ compared different ways of creating piecewise regression models. All of these models are equivalent in that the overall test of the model is exactly the same ( always F( 3, 196) = 210.66) and that they all generate the exact predicted values. The differences in parameterization are merely a rescrambling of the intercepts and slopes for the two segments of the regression model. You can choose the coding strategy that you like best, but note that you can use lincom to combine or compare coefficients to form comparisons that were not present in the original model. While the mkspline command is very convenient, some might prefer the manual coding schemes we illustrated because of the interpretation they provide with respect to the intercept terms.