Multiple regression models often contain interaction terms. This FAQ page covers the situation in which there are two moderator variables which jointly influence the regression of the dependent variable on an independent variable. In other words, a regression model that has a significant three-way interaction of continuous variables.
If you are new to the topic of interactions of continuous variables, you may want to start with the FAQ page the discusses the simpler continuous by continuous two-way interaction, How can I explain a continuous by continuous interaction?
Back to the three-way interaction. There are several approaches that one might use to explain a three-way interaction. The approach that we will demonstrate is to compute simple slopes, i.e., the slopes of the dependent variable on the independent variable when the moderator variables are held constant at different combinations of high and low values. After computing the simple slopes, we will then compute and test the differences among all pairs of the slopes. The method used in this FAQ is adapted from a paper by Dawson and Richter (2004). The Dawson and Richter method computes the differences in simple slopes and their standard errors using a number of moderately-complex formulas. We will take an easier path and let margins do all of the heavy lifting.
We will begin by looking at the regression equation which includes a three-way continuous interaction. In the formula, Y is the response variable, X the predictor (independent) variable with Z and W being the two moderator variables.
Y = b0 + b1X + b2Z + b3W + b4XZ + b5XW + b6ZW + b7XZW
We can reorder the terms into two groups, the first grouping (terms that do not contain X) defines the intercept while the second grouping (all the terms that contain an X) defines the simple slope.
Y = (b0 + b2Z + b3W + b6ZW) + (b1 + b4Z + b5W + b7ZW)X
Next, we will define high values of Z and W as being one standard deviation above their respective means and will denote them as Hz and Hw. The low values will be defined as one standard deviation below their means and will be as Lz and Lw. Altogether there are four possible combinations of conditions: 1) HzHw, 2) HzLw, 3) LzHw and 4) LzLw.
Here is the formula for the simple slope for condition 1) when both Z and W are at their high values. The formulas for the other three conditions are exactly the same except that the values for Z and W are different.
simple slope 1 = b1 + b4Hz + b5Hw + b7HzHw
We will illustrate the simple slopes process using the dataset hsb2 that has a statistically significant (barely) three-way continuous interaction. In order to keep the notation consistent we will temporarily change the names of the variables; y for the response variable, x for the independent variable, z for the first moderator, and w for the second moderator. It is clear from the code below that write is the response variable, read is the IV and math and science are the moderator variables.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2, clear
rename write y
rename read x
rename math w
rename science z
regress y c.x##c.z##c.w
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 26.28
Model | 8748.54751 7 1249.7925 Prob > F = 0.0000
Residual | 9130.32749 192 47.553789 R-squared = 0.4893
-------------+------------------------------ Adj R-squared = 0.4707
Total | 17878.875 199 89.843593 Root MSE = 6.8959
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | -3.013849 1.802977 -1.67 0.096 -6.570035 .5423358
z | -2.435316 1.757363 -1.39 0.167 -5.901532 1.0309
|
c.x#c.z | .0553139 .0325207 1.70 0.091 -.0088297 .1194576
|
w | -3.228097 1.926393 -1.68 0.095 -7.027708 .5715142
|
c.x#c.w | .0737523 .035898 2.05 0.041 .0029472 .1445575
|
c.z#c.w | .0611136 .035031 1.74 0.083 -.0079813 .1302086
|
c.x#c.z#c.w | -.0012563 .0006277 -2.00 0.047 -.0024944 -.0000182
|
_cons | 166.5438 93.12788 1.79 0.075 -17.1413 350.2289
------------------------------------------------------------------------------
Please note that the three-way interaction, xzw, is statistically significant with a p-value of .047.
We will create four global macros that contain the values w and z when that are one standard deviation above the mean and one standard deviation below the mean.
/* determine range of x for graphing */
sum x
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
x | 200 52.23 10.25294 28 76
sum w
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
w | 200 52.645 9.368448 33 75
/* determined high and low values for w */
global Hw=r(mean)+r(sd)
global Lw=r(mean)-r(sd)
sum z
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
z | 200 51.85 9.900891 26 74
/* determine high and low values for z */
global Hz=r(mean)+r(sd)
global Lz=r(mean)-r(sd)
We will use the margins comand to compute the simple slopes for the four values of w and z. We use the dydx option to obtain the slopes. Please note, we have manually annotated the output with the various combinations of w and z in parentheses.
margins, dydx(x) at(w=($Hw $Lw) z=($Hz $Lz)) vsquish
Average marginal effects Number of obs = 200
Model VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : x
1._at : z = 61.75089
w = 62.01345
2._at : z = 61.75089
w = 43.27655
3._at : z = 41.94911
w = 62.01345
4._at : z = 41.94911
w = 43.27655
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x |
_at |
(HwHz) 1 | .164556 .0953841 1.73 0.084 -.0223935 .3515054
(LwHz) 2 | .236248 .1429934 1.65 0.099 -.0440138 .5165098
(HwLz) 3 | .6119673 .1962032 3.12 0.002 .227416 .9965186
(LwLz) 4 | .2175364 .1275474 1.71 0.088 -.0324519 .4675248
------------------------------------------------------------------------------
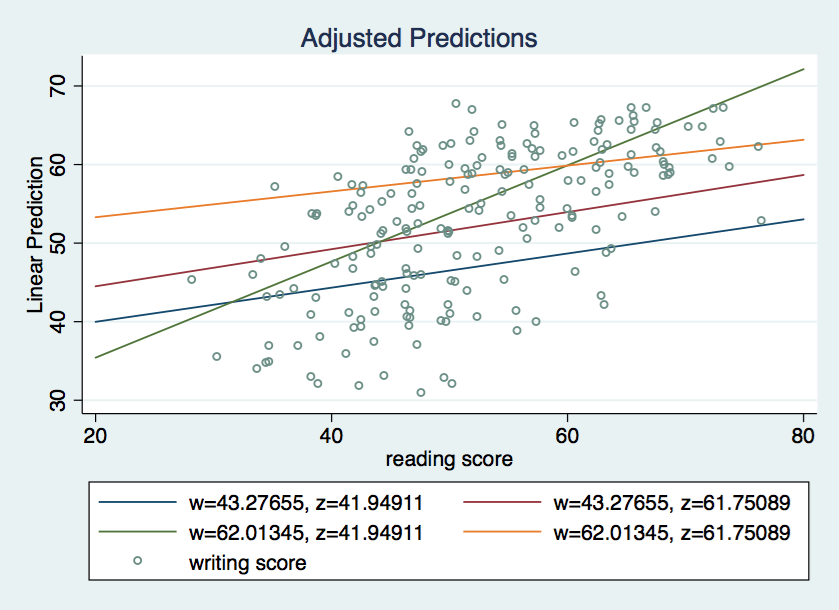
The simple slopes for HwHz, LwHz and LwLz are all fairly similar. However, the slope for Hwlz seems to be rather different from the other three.
The next step is to graph the slopes along with a scatterplot of the observations. We will use the margins command again to get the information for plotting. Because we are using linear regression, we need only two points to define each simple slope regression line. We will use the x values 20 and 80 which cover more the full range of variable x.
(introduced in Stata 12) command.
margins, at(x=(20 80) w=($Hw $Lw) z=($Hz $Lz)) vsquish
Adjusted predictions Number of obs = 200
Model VCE : OLS
Expression : Linear prediction, predict()
1._at : x = 20
z = 61.75089
w = 62.01345
2._at : x = 20
z = 61.75089
w = 43.27655
3._at : x = 20
z = 41.94911
w = 62.01345
4._at : x = 20
z = 41.94911
w = 43.27655
5._at : x = 80
z = 61.75089
w = 62.01345
6._at : x = 80
z = 61.75089
w = 43.27655
7._at : x = 80
z = 41.94911
w = 62.01345
8._at : x = 80
z = 41.94911
w = 43.27655
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | 53.29426 4.059313 13.13 0.000 45.33815 61.25037
2 | 44.50291 5.033491 8.84 0.000 34.63745 54.36837
3 | 35.41995 6.802609 5.21 0.000 22.08708 48.75282
4 | 39.98077 3.033838 13.18 0.000 34.03455 45.92698
5 | 63.16762 1.926701 32.79 0.000 59.39135 66.94388
6 | 58.67779 4.006649 14.65 0.000 50.8249 66.53068
7 | 72.13799 5.488377 13.14 0.000 61.38097 82.89501
8 | 53.03295 4.786994 11.08 0.000 43.65062 62.41529
------------------------------------------------------------------------------
Next, we use the marginsplot command (introduced in Stata 12) to do the actual plotting. The addplot option allows us to include a scatterplot of the observations along with the simple slope regression lines.
marginsplot, recast(line) noci addplot(scatter y x, msym(oh) jitter(3))
Now we have a good idea of what is going on with these data.
Hey, wait a minute, my model also has covariates. What about them? We will deal with adding covariates to the model in the next section.
Three-way interaction of continuous variables with covariates
Here is the regression model from the previous page with two covariates V1 and V2 added.
Y = b0 + b1X + b2Z + b3W + b4XZ + b5XW + b6ZW + b7XZW + b8V1 + b9V2
Adding covariates to your model does not change the formulas for the simple slopes as long as the covariates are not interacted with the independent variable or the moderator variables.
We will add two covariates to our previous model, socst which will be renamed as v1 and ses which will be renamed v2. Everything is this section is the same as the previous example with the exception of adding the covariates to the end of the regress command.
rename socst v1
rename ses v2
regress y c.x##c.z##c.w v1 v2
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 9, 190) = 25.36
Model | 9757.27668 9 1084.14185 Prob > F = 0.0000
Residual | 8121.59832 190 42.7452543 R-squared = 0.5457
-------------+------------------------------ Adj R-squared = 0.5242
Total | 17878.875 199 89.843593 Root MSE = 6.538
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | -3.463037 1.716525 -2.02 0.045 -6.848932 -.0771426
z | -2.902201 1.670106 -1.74 0.084 -6.196533 .3921302
|
c.x#c.z | .0624411 .03093 2.02 0.045 .0014308 .1234514
|
w | -3.696588 1.831366 -2.02 0.045 -7.309009 -.0841671
|
c.x#c.w | .0796921 .0341529 2.33 0.021 .0123245 .1470597
|
c.z#c.w | .0696334 .0332851 2.09 0.038 .0039775 .1352893
|
c.x#c.z#c.w | -.0013838 .0005968 -2.32 0.021 -.0025611 -.0002065
|
v1 | .2789791 .057697 4.84 0.000 .1651703 .392788
v2 | -.9056562 .6914623 -1.31 0.192 -2.269585 .4582727
_cons | 185.3134 88.56438 2.09 0.038 10.6177 360.0092
------------------------------------------------------------------------------
Note that with the inclusion the covariates that the three-way interaction is even “more” significant than before.
Next, we will compute the simple slopes for the various combinations of w and z. The margins command is exactly the same as for the example without the covariates because the covariances are not involved in the 3-way interaction.
/* compute simple slopes */
margins, dydx(x) at(w=($Hw $Lw) z=($Hz $Lz)) vsquish
Average marginal effects Number of obs = 200
Model VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : x
1._at : z = 61.75089
w = 62.01345
2._at : z = 61.75089
w = 43.27655
3._at : z = 41.94911
w = 62.01345
4._at : z = 41.94911
w = 43.27655
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x |
_at |
1 | .0356648 .0951734 0.37 0.708 -.1508717 .2222012
2 | .1435565 .1371306 1.05 0.295 -.1252146 .4123276
3 | .498484 .1884961 2.64 0.008 .1290384 .8679296
4 | .0929561 .1236172 0.75 0.452 -.1493291 .3352413
------------------------------------------------------------------------------
Let’s plot the four simple slopes on top of the observations. We begin the graphing by computing expected values using the margins command for different values of ww and z. Again, we need only two values of x (20 & 80) to define each simple slope regression line.
margins, at(x=(20 80) w=($Hw $Lw) z=($Hz $Lz)) vsquish
Predictive margins Number of obs = 200
Model VCE : OLS
Expression : Linear prediction, predict()
1._at : x = 20
z = 61.75089
w = 62.01345
2._at : x = 20
z = 61.75089
w = 43.27655
3._at : x = 20
z = 41.94911
w = 62.01345
4._at : x = 20
z = 41.94911
w = 43.27655
5._at : x = 80
z = 61.75089
w = 62.01345
6._at : x = 80
z = 61.75089
w = 43.27655
7._at : x = 80
z = 41.94911
w = 62.01345
8._at : x = 80
z = 41.94911
w = 43.27655
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | 56.98694 3.936984 14.47 0.000 49.27059 64.70329
2 | 47.84013 4.825798 9.91 0.000 38.38174 57.29852
3 | 38.20389 6.500797 5.88 0.000 25.46256 50.94522
4 | 44.62434 3.040215 14.68 0.000 38.66563 50.58306
5 | 59.12683 2.060024 28.70 0.000 55.08925 63.1644
6 | 56.45352 3.835255 14.72 0.000 48.93656 63.97048
7 | 68.11293 5.302337 12.85 0.000 57.72054 78.50532
8 | 50.20171 4.580553 10.96 0.000 41.22399 59.17943
------------------------------------------------------------------------------
marginsplot, recast(line) noci addplot(scatter y x, msym(oh) jitter(3))
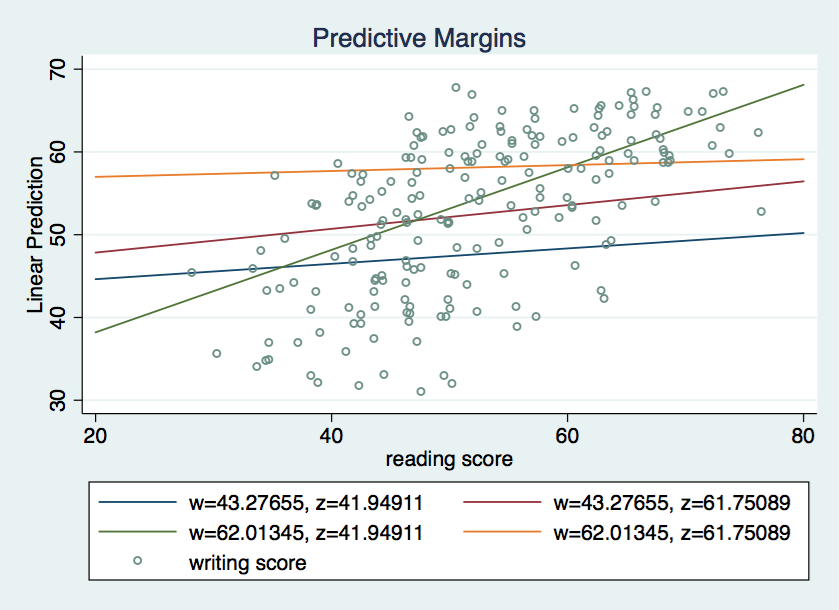
With the covariates in the model we have a bit more variation in the simple slopes. However, once again it looks like slope 3 is the one that is the most different from the others.
We can compute tests of differences in simple slopes using the pwcompare(effects) option for margins. This option was introduced in Stata 12.
/* compute pairwise differences in simple slopes */
margins, dydx(x) at(w=($Hw $Lw) z=($Hz $Lz)) vsquish pwcompare(effects)
Pairwise comparisons of average marginal effects
Model VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : x
1._at : z = 61.75089
w = 62.01345
2._at : z = 61.75089
w = 43.27655
3._at : z = 41.94911
w = 62.01345
4._at : z = 41.94911
w = 43.27655
------------------------------------------------------------------------------
| Contrast Delta-method Unadjusted Unadjusted
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x |
_at |
2 vs 1 | .1078917 .1559956 0.69 0.489 -.197854 .4136375
3 vs 1 | .4628192 .1955057 2.37 0.018 .0796352 .8460033
4 vs 1 | .0572913 .1557822 0.37 0.713 -.2480361 .3626188
3 vs 2 | .3549275 .2449055 1.45 0.147 -.1250785 .8349335
4 vs 2 | -.0506004 .1635762 -0.31 0.757 -.3712038 .2700031
4 vs 3 | -.4055279 .2096843 -1.93 0.053 -.8165015 .0054457
------------------------------------------------------------------------------
Inspecting the table above it appears slope 3 versus slope 1 (LzHw vs HzHw) is the only one of the tests that is significant. But before we reach that conclusion we will need to adjust the p-values to take into account that these are post-hoc tests. To do this, we will add the mcompare(bonferroni) option to the margins command.
/* compute pairwise differences in simple slopes with Bonferroni correction */
margins, dydx(x) at(w=($Hw $Lw) z=($Hz $Lz)) vsquish pwcompare(effects) mcompare(bonferroni)
Pairwise comparisons of average marginal effects
Model VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : x
1._at : z = 61.75089
w = 62.01345
2._at : z = 61.75089
w = 43.27655
3._at : z = 41.94911
w = 62.01345
4._at : z = 41.94911
w = 43.27655
---------------------------
| Number of
| Comparisons
-------------+-------------
x |
_at | 6
---------------------------
------------------------------------------------------------------------------
| Contrast Delta-method Bonferroni Bonferroni
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x |
_at |
2 vs 1 | .1078917 .1559956 0.69 1.000 -.3036648 .5194483
3 vs 1 | .4628192 .1955057 2.37 0.108 -.052975 .9786135
4 vs 1 | .0572913 .1557822 0.37 1.000 -.3537022 .4682849
3 vs 2 | .3549275 .2449055 1.45 0.884 -.2911963 1.001051
4 vs 2 | -.0506004 .1635762 -0.31 1.000 -.4821564 .3809557
4 vs 3 | -.4055279 .2096843 -1.93 0.319 -.9587289 .1476731
------------------------------------------------------------------------------
With the Bonferroni correction the p-value for 3 vs 1 becomes 0.108, which is not statistically significant. The Bonferroni correction may not be the best choice because it is overly conservative but it is certainly easy to implement.
References
Dawson, J.F. & Richter, A.W. (2004) A significance test of slope differences for three-way interactions in moderated multiple regression analysis. RP0422. Aston University, Birmingham, UK