The techniques and methods for this FAQ page were inspired Long (2006) and Hu & Long (2005).
This FAQ page uses features available in Stata 11 and will not work for earlier versions. If you are using an earlier version of Stata go to FAQ page.
Interactions in logistic regression models can be trickier than interactions in comparable OLS regression.
Many researchers are not comfortable interpreting the results in terms of the raw coefficients which are scaled in terms of log odds. The interpretation of interactions in log odds is done basically the same way as in OLS regression. However, many researchers prefer to interpret results in terms of probabilities. The shift from log odds to probabilities is a nonlinear transformation which means that the interactions are no longer a simple linear function of the predictors.
This FAQ page will try to help you to understand categorical by continuous interactions in logistic regression models both with and without covariates.
We will use an example dataset, logitcatcon, that has one binary predictor, f, which stands for female and one continuous predictor s. In addition, the model will include fs which is the f by s interaction. We will begin by loading the data and then running the logit model.
use https://stats.idre.ucla.edu/stat/data/logitcatcon, clear
logit y i.f##c.s, nolog
Logistic regression Number of obs = 200
LR chi2(3) = 71.01
Prob > chi2 = 0.0000
Log likelihood = -96.28586 Pseudo R2 = 0.2694
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.f | 5.786811 2.302518 2.51 0.012 1.273959 10.29966
s | .1773383 .0364362 4.87 0.000 .1059248 .2487519
|
f#c.s |
1 | -.0895522 .0439158 -2.04 0.041 -.1756255 -.0034789
|
_cons | -9.253801 1.94189 -4.77 0.000 -13.05983 -5.447767
------------------------------------------------------------------------------
As you can see all of the variables in the above model including the interaction term are statistically significant. If this were an OLS regression model we could do a very good job of understanding the interaction using just the coefficients in the model. The situation in logistic regression is more complicated because the value of the interaction effect changes depending upon the value of the continuous predictor variable. To begin to understand what is going on consider the Table 1 below.
Table 1: Predicted probabilities when s=40
f=0 f=1 change LB UB
.1034 .5111 .4077 .2182 .5972
Table 1 contains predicted probabilities, differences in predicted probabilities and the confidence interval of the difference in predicted probabilities while holding the continuous predictor at 40. The first value, .1034, is the predicted probability when f=0 (males), the .5111 when f=1 (females). The third value, .4077, is the difference in probabilities for males and females. The next two values are the 95% confidence interval on the difference in probabilities. If the confidence interval contains zero the difference would not be considered statistically significant. In our example, the confidence interval does not contain zero, thus, the difference in probabilities is statistically significant.
To get the values for Table 1 we will run margins with the post option followed by the lincom command.
margins f, at(s=40) post
Adjusted predictions Number of obs = 200
Model VCE : OIM
Expression : Pr(y), predict()
at : s = 40
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
f |
0 | .1033756 .0500784 2.06 0.039 .0052238 .2015275
1 | .5111116 .0827069 6.18 0.000 .349009 .6732142
------------------------------------------------------------------------------
lincom 1.f-0.f
( 1) - 0bn.f + 1.f = 0
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .407736 .0966865 4.22 0.000 .2182339 .597238
------------------------------------------------------------------------------
Now that we know how to compute the difference in probabilities including the confidence interval, we need to do this for a whole rang of values of s. Because we used margins with the post option we will need to rerun the logit command again. We will save the results from the lincom command into a matrix called t along with the values of the continuous variable. Finally, we save the matrix back into the dataset and graph the results.
logit y f##c.s, nolog
margins f, at(s=(20(2)70)) post
mat t = e(at)
mat t = t[1...,"s"]
mat t = t,J(26,3,.)
forvalue i=1/26 {
quietly lincom _b[`i'._at#1.f]-_b[`i'._at#0.f]
mat t[`i',2] = r(estimate)
mat t[`i',3] = r(estimate) - 1.96*r(se)
mat t[`i',4] = r(estimate) + 1.96*r(se)
}
mat colnames t = at dif ll ul
svmat t, names(col)
twoway (line dif at)(line ll at)(line ul at), ///
yline(0) legend(off) ///
xtitle(continuous independent variable) ytitle(probability difference) ///
title(male-female difference) scheme(lean1)
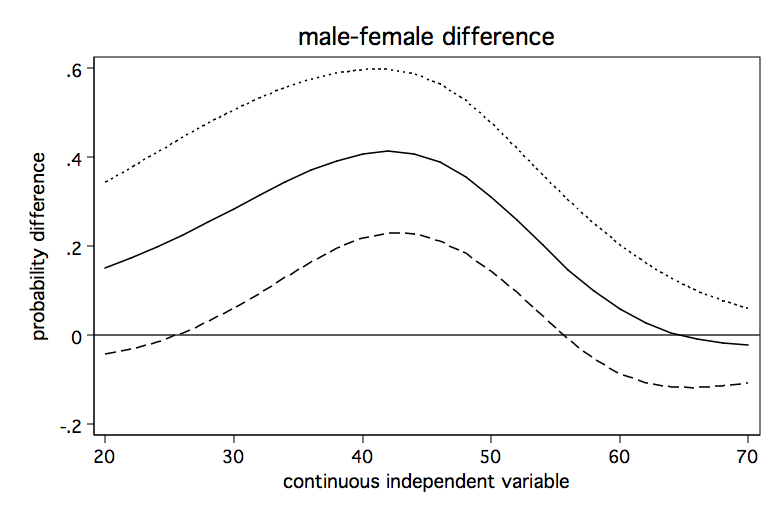
Now, we will run the above code fragment and check out the graph.
The above graph shows how the male-female probability difference varies with changes in the value of s. It appears that the difference in probabilities for male and females is statistically significant between values of s of approximately 28 to 55 and is nonsignificant elsewhere.
There is another way that we could compute the male/female difference in probability more directly. We will use the margins command again along with the user written command parmest by Roger Newson (search parmest). Here is what the steps look like.
quietly logit y i.f##c.s
margins, dydx(f) at(s=(20(2)70)) vsquish post
Conditional marginal effects Number of obs = 200
Model VCE : OIM
Expression : Pr(y), predict()
dy/dx w.r.t. : 1.f
1._at : s = 20
2._at : s = 22
3._at : s = 24
4._at : s = 26
5._at : s = 28
6._at : s = 30
7._at : s = 32
8._at : s = 34
9._at : s = 36
10._at : s = 38
11._at : s = 40
12._at : s = 42
13._at : s = 44
14._at : s = 46
15._at : s = 48
16._at : s = 50
17._at : s = 52
18._at : s = 54
19._at : s = 56
20._at : s = 58
21._at : s = 60
22._at : s = 62
23._at : s = 64
24._at : s = 66
25._at : s = 68
26._at : s = 70
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.f |
_at |
1 | .1496878 .0987508 1.52 0.130 -.0438602 .3432358
2 | .1724472 .1043526 1.65 0.098 -.0320801 .3769745
3 | .1975119 .1089189 1.81 0.070 -.0159653 .4109891
4 | .2246979 .1121624 2.00 0.045 .0048636 .4445323
5 | .2536377 .1138457 2.23 0.026 .0305042 .4767711
6 | .2837288 .1138312 2.49 0.013 .0606236 .5068339
7 | .3140793 .1121391 2.80 0.005 .0942908 .5338679
8 | .3434564 .1090032 3.15 0.002 .1298141 .5570987
9 | .3702468 .104906 3.53 0.000 .1646348 .5758589
10 | .3924501 .100548 3.90 0.000 .1953797 .5895206
11 | .407736 .0966865 4.22 0.000 .2182339 .5972381
12 | .4136138 .0938187 4.41 0.000 .2297325 .5974952
13 | .4077687 .0918544 4.44 0.000 .2277375 .5878
14 | .3885877 .0901228 4.31 0.000 .2119502 .5652252
15 | .3558056 .0879135 4.05 0.000 .1834983 .5281129
16 | .311046 .0851843 3.65 0.000 .1440879 .4780041
17 | .2579152 .0826761 3.12 0.002 .0958731 .4199574
18 | .2014085 .0810274 2.49 0.013 .0425978 .3602192
19 | .146748 .0798151 1.84 0.066 -.0096868 .3031828
20 | .09816 .0778372 1.26 0.207 -.0543981 .2507182
21 | .0581376 .0741941 0.78 0.433 -.0872801 .2035553
22 | .0273908 .0688343 0.40 0.691 -.1075218 .1623035
23 | .0052927 .0623354 0.08 0.932 -.1168824 .1274678
24 | -.0095202 .0554486 -0.17 0.864 -.1181975 .0991571
25 | -.0186421 .0487849 -0.38 0.702 -.1142588 .0769746
26 | -.0235782 .042708 -0.55 0.581 -.1072843 .0601279
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
mat at=e(at)
mat at=at[1...,"s"]
Notice that we used dydx(f) in the margins command which computes a discrete difference between males and females for each value of c. Next, we will use the parmest command which will replace the data in memory with vales of the estimate and confidence intervals.
parmest, fast drop if z==. drop eq parm svmat at twoway (line estimate at1)(line min95 at1)(line max95 at1), /// legend(off) yline(0) /// xtitle(continuous independent variable) ytitle(probability difference) /// title(male-female difference) scheme(lean1)
The graph produced by the twoway command is exactly the same as the one shown above.
So, that went fairly well but what if there was a covariate in the model? The model below includes the covariate cv1.
use https://stats.idre.ucla.edu/stat/data/logitcatcon, clear
logit y f##c.s cv1, nolog
Logistic regression Number of obs = 200
LR chi2(4) = 114.41
Prob > chi2 = 0.0000
Log likelihood = -74.587842 Pseudo R2 = 0.4340
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.f | 9.983662 3.05269 3.27 0.001 4.0005 15.96682
s | .1750686 .0470033 3.72 0.000 .0829438 .2671933
|
f#c.s |
1 | -.1595233 .0570352 -2.80 0.005 -.2713103 -.0477363
|
cv1 | .1877164 .0347888 5.40 0.000 .1195316 .2559013
_cons | -19.00557 3.371064 -5.64 0.000 -25.61273 -12.39841
------------------------------------------------------------------------------
As before, all of the coefficients are statistically significant.
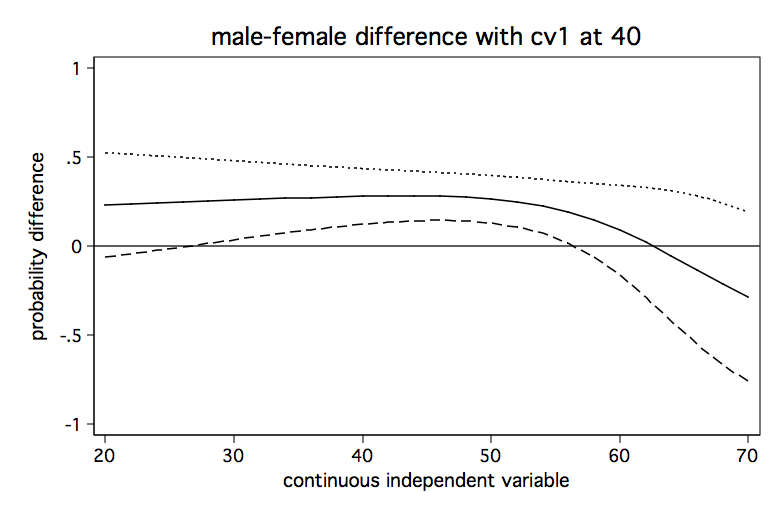
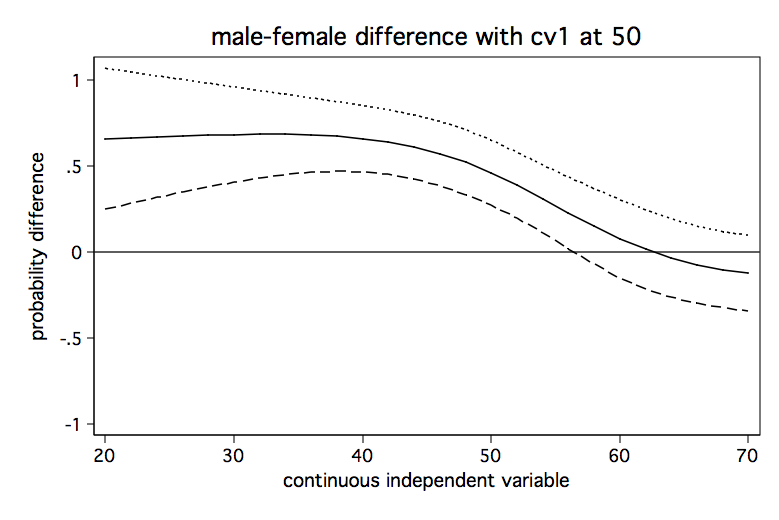
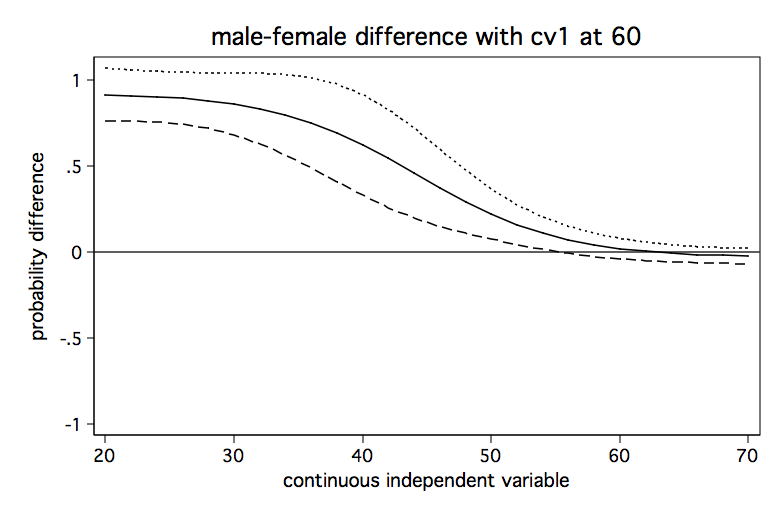
We will run the analysis pretty much as before except that we will do it three times holding the covariate at a different value each time. We begin holding the covariate at a low value of 40, then at a medium value of 50 and finally at a high value of 60. The code fragment below computes the predicted differences in probability for each of the three values of the covariate and produces a separate graph for each one.
/* hold cv1 at 40 */
drop at-ul
logit y f##c.s cv1, nolog
margins f, at(s=(20(2)70) cv1=40) post
mat t = e(at)
mat t = t[1...,"s"]
mat t = t,J(26,3,.)
forvalue i=1/26 {
quietly lincom _b[`i'._at#1.f]-_b[`i'._at#0.f]
mat t[`i',2] = r(estimate)
mat t[`i',3] = r(estimate) - 1.96*r(se)
mat t[`i',4] = r(estimate) + 1.96*r(se)
}
mat colnames t = at dif ll ul
svmat t, names(col)
twoway (line dif at)(line ll at)(line ul at), ///
yline(0) legend(off) ylabel(-1(.5)1) ///
xtitle(continuous independent variable) ytitle(probability difference) ///
title(male-female difference with cv1 at 40) scheme(lean1)
/* hold cv1 at 50 */
drop at-ul
logit y f##c.s cv1, nolog
margins f, at(s=(20(2)70) cv1=50) post
forvalue i=1/26 {
quietly lincom _b[`i'._at#1.f]-_b[`i'._at#0.f]
mat t[`i',2] = r(estimate)
mat t[`i',3] = r(estimate) - 1.96*r(se)
mat t[`i',4] = r(estimate) + 1.96*r(se)
}
svmat t, names(col)
twoway (line dif at)(line ll at)(line ul at), ///
yline(0) legend(off) ylabel(-1(.5)1) ///
xtitle(continuous independent variable) ytitle(probability difference) ///
title(male-female difference with cv1 at 50) scheme(lean1)
/* hold cv1 at 60 */
drop at-ul
logit y f##c.s cv1, nolog
margins f, at(s=(20(2)70) cv1=60) post
forvalue i=1/26 {
quietly lincom _b[`i'._at#1.f]-_b[`i'._at#0.f]
mat t[`i',2] = r(estimate)
mat t[`i',3] = r(estimate) - 1.96*r(se)
mat t[`i',4] = r(estimate) + 1.96*r(se)
}
svmat t, names(col)
twoway (line dif at)(line ll at)(line ul at), ///
yline(0) legend(off) ylabel(-1(.5)1) ///
xtitle(continuous independent variable) ytitle(probability difference) ///
title(male-female difference with cv1 at 60) scheme(lean1)
It seems clear from looking at the three graphs that the male-female difference in probability increases as cv1 increases except for high values of s. And, yes, I know the upper limit of the confidence interval exceeds one in some places but that is just an artifact of how the confidence intervals were created. We aren’t really trying to imply that the probability can ever exceed one.
References
Long, J. S. 2006. Group comparisons and other issues in interpreting models for categorical
outcomes using Stata. Presentation at 5th North American Users Group Meeting. Boston,
Massachusetts.
Xu, J. and J.S. Long, 2005. Confidence intervals for predicted outcomes in regression models for
categorical outcomes. The Stata Journal 5: 537-559.