When analyzing geospatial data, describing the spatial pattern of a measured variable is of great importance. User written Stata commands allow you to explore such patterns. This page will use the variog and variog2 command. To install this, type search variog in your command window.
The variog command allows you to calculate and graph a variogram for regularly spaced one-dimensional data. The variog2 command allows you to calculate and graph a variogram for two-dimensional data without constraints on spacing. In both cases, the variogram illustrates how differences in a measured variable Z vary as the distances between the points at which Z is measured increase.
Let’s look at an example. Our dataset contains ozone measurements from thirty-two locations in the Los Angeles area aggregated over one month. The dataset includes the station number (station), the latitude and longitude of the station (lat and lon), and the average of the highest eight hour daily averages (av8top). This data, and other spatial datasets, can be downloaded from the GeoDa Center for Geospatial Analysis and Computation.
use https://stats.idre.ucla.edu/stat/stata/faq/ozone, clear
clist in 1/5
station av8top lat lon
1. 60 7.225806 34.13583 -117.9236
2. 69 5.899194 34.17611 -118.3153
3. 72 4.052885 33.82361 -118.1875
4. 74 7.181452 34.19944 -118.5347
5. 75 6.076613 34.06694 -117.7514
For the sake of an example, let’s imagine that instead of specific latitude and longitude locations, the stations are evenly spaced along a single latitude. If we assume the observations are in the order in which the stations appear, we can use the variog command. In the command, we indicate the measured outcome and we will opt for the calculated values to be listed. By default, a plot of the semi-variogram will be generated.
variog av8top, list +----------------------------------+ | Lag Semi-variance # of pairs | |----------------------------------| | 1 2.328506 31 | | 2 2.615086 30 | | 3 2.629862 29 | | 4 2.983584 28 | | 5 3.415026 27 | |----------------------------------| | 6 2.923007 26 | | 7 4.104437 25 | | 8 3.378503 24 | | 9 3.531528 23 | | 10 4.49281 22 | |----------------------------------| | 11 5.22965 21 | | 12 6.657857 20 | | 13 6.5462 19 | | 14 6.126221 18 | | 15 6.556983 17 | |----------------------------------| | 16 6.451519 16 | +----------------------------------+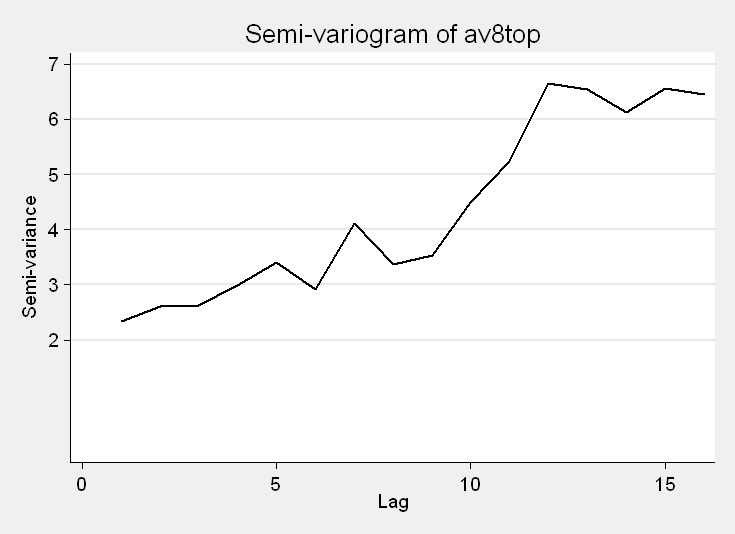
Next, let’s generate a variogram using the latitude and longitude of the stations. For this, we will use the variog2 command. While the lag distance in variog was assumed to be the distance between each evenly spaced observation, variog2 requires the user to specify the lag distance. Let’s look at a summary of our coordinates to get a sense of the distances existing in our data.
summarize lat lon
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
lat | 32 34.0146 .2228168 33.6275 34.69012
lon | 32 -117.7078 .5683853 -118.5347 -116.2339
Based on this, we can calculate the maximum possible distance we might see in our data.
dis sqrt((33.6275 - 34.69012)^2 + (-118.5347 - -116.2339)^2) 2.5343326
As a starting point, we can choose a lag distance of .1 and we can examine distances up to 12 lags apart. We want to choose a lag distance that yields enough pairs in each lag to generate a variance that we trust. We might aim to have at least 15 pairs in each lag.
variog2 av8top lat lon, width(.1) lags(12) list +----------------------------------+ | Lag Semi-variance # of pairs | |----------------------------------| | 1 4.729442 6 | | 2 1.8984963 31 | | 3 1.3789778 41 | | 4 2.7462469 50 | | 5 4.3899238 49 | |----------------------------------| | 6 4.1974818 43 | | 7 5.2652506 48 | | 8 7.3351494 41 | | 9 6.8823236 36 | | 10 8.0089961 29 | |----------------------------------| | 11 6.6957223 29 | | 12 7.1360346 23 | +----------------------------------+
We can see that our first lag contains only 6 pairs. We might increase the size of our lags and look at fewer of them.
variog2 av8top lat lon, width(.15) lags(10) list +----------------------------------+ | Lag Semi-variance # of pairs | |----------------------------------| | 1 1.8485044 21 | | 2 1.8412199 57 | | 3 3.1204523 74 | | 4 4.4411303 68 | | 5 5.8693088 70 | |----------------------------------| | 6 7.0979125 55 | | 7 7.8960334 44 | | 8 6.5713557 37 | | 9 4.0710902 23 | | 10 3.3176015 16 | +----------------------------------+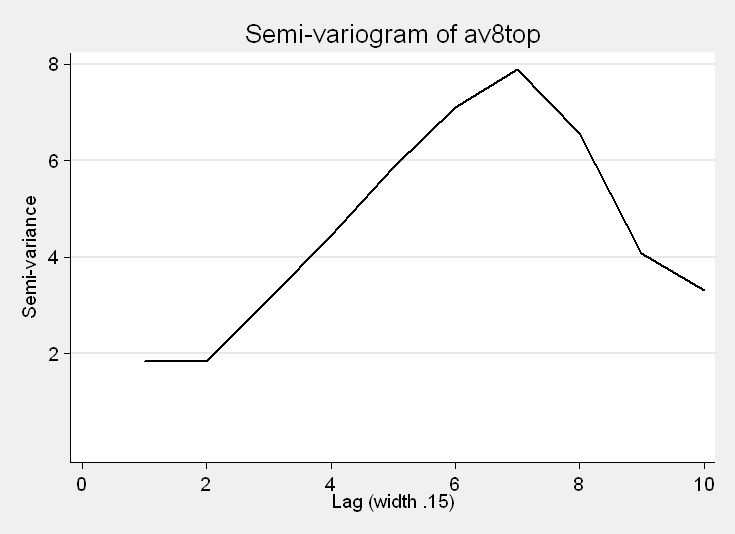
In the output, we can see lag distances up to 10*.15 = 1.5, the number of pairs that are this far apart in the dataset, and the semi-variance. As we can see from the plot, the semi-variance increases until the lag distance exceeds .15*7 = 1.05.
References:
- Cressie, Noel. Statistics for Spatial Data. John Wiley & Sons, Inc.: New York, 1991.
