Graphing results from the margins command can help in the interpretation of your model. Almost all of the needed results will be found in various matrices saved by margins. If you do not use the post option the matrices of interest are r(b) which has the point estimates, r(V) the variance-covariance matrix (standard errors are squares roots of the diagonal values), and r(at) which has the values used in the at option. If you do use the post option then the relevant matrices are e(b), e(V) and e(at).
Generally, the point estimates will be plotted on the y-axis. The x-axis will either be the at values or levels of a categorical predictor. The general strategy shown here will show how to get the necessary values for graphing into a Stata matrix which we will then save to data in memory using the svmat command. Once the values are part of the data we can plot the points using standard graph commands.
Example 1
Let’s start with a model that has a categorical by categorical interaction along with two continuous covariates. We will run the model as an anova but we would get the same results if we ran it as a regression.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
anova write prog##female math read
Number of obs = 200 R-squared = 0.6932
Root MSE = 6.59748 Adj R-squared = 0.5155
Source | Partial SS df MS F Prob > F
------------+----------------------------------------------------
Model | 12394.507 73 169.787767 3.90 0.0000
|
prog | 22.3772184 2 11.1886092 0.26 0.7737
female | 1125.44586 1 1125.44586 25.86 0.0000
prog#female | 287.95987 2 143.979935 3.31 0.0398
math | 2449.19165 39 62.799786 1.44 0.0670
read | 2015.49976 29 69.4999916 1.60 0.0411
|
Residual | 5484.36799 126 43.5267301
------------+----------------------------------------------------
Total | 17878.875 199 89.843593
Next, we run the margins command to get the six adjust cell means from the 2 by 3 interaction. These adjusted cells means are called lsmeans in SAS or estimated marginal means in SPSS. After the margins command we will list the r(b) matrix.
margins prog#female, asbalanced
Adjusted predictions Number of obs = 200
Expression : Linear prediction, predict()
at : prog (asbalanced)
female (asbalanced)
math (asbalanced)
read (asbalanced)
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog#female |
1 0 | 50.43791 1.969439 25.61 0.000 46.57788 54.29794
1 1 | 56.9152 1.948113 29.22 0.000 53.09697 60.73343
2 0 | 52.58387 1.408514 37.33 0.000 49.82323 55.34451
2 1 | 55.05205 1.41875 38.80 0.000 52.27136 57.83275
3 0 | 47.81982 2.108078 22.68 0.000 43.68806 51.95158
3 1 | 57.29057 1.785628 32.08 0.000 53.79081 60.79034
------------------------------------------------------------------------------
matrix list r(b)
r(b)[1,6]
1.prog# 1.prog# 2.prog# 2.prog# 3.prog# 3.prog#
0.female 1.female 0.female 1.female 0.female 1.female
r1 50.437911 56.9152 52.583868 55.052054 47.81982 57.290573
Note that r(b) is a 1×6 matrix. We will want the 6×1 transpose of r(b) which we will call b.
matrix b=r(b)'
matrix list b
b[6,1]
r1
1.prog#
0.female 50.437911
1.prog#
1.female 56.9152
2.prog#
0.female 52.583868
2.prog#
1.female 55.052054
3.prog#
0.female 47.81982
3.prog#
1.female 57.290573
If you look back at the margins output you will see a column for prog that has two 1’s followed by two 2’s and then two 3’s. We will create this array using a Kronecker product of a column vector (123) and a column vector (11).
matrix prg=(123)#(11) /* # is the kronecker product operator */
matrix list prg
prg[6,1]
c1:
c1
r1:r1 1
r1:r2 1
r2:r3 2
r2:r4 2
r3:r5 3
r3:r6 3
We will use this same trick again to create an series of alternating 0’s and 1’s. Next, we will combine the three columns together into a matrix called c.
matrix fem=(111)#(01) /* # is the kronecker product operator */
matrix list fem
fem[6,1]
c1:
c1
r1:r1 0
r1:r2 1
r2:r3 0
r2:r4 1
r3:r5 0
r3:r6 1
matrix c=prg,fem,b
matrix list c
c[6,3]
c1: c1:
c1 c1 r1
r1:r1 1 0 50.437911
r1:r2 1 1 56.9152
r2:r3 2 0 52.583868
r2:r4 2 1 55.052054
r3:r5 3 0 47.81982
r3:r6 3 1 57.290573
Now we can save c to data using the svmat command.
svmat c, names(c)
clist c1-c3 in 1/7
c1 c2 c3
1. 1 0 50.43791
2. 1 1 56.9152
3. 2 0 52.58387
4. 2 1 55.05206
5. 3 0 47.81982
6. 3 1 57.29057
7. . . .
We can now plot the adjusted cell means for prog by female using graph twoway
/* plot prog by female */
graph twoway (connect c3 c1 if c2==0)(connect c3 c1 if c2==1), ///
xlabel(1 2 3) legend(order(1 "female=0" 2 "female=1")) ///
xtitle(prog) ytitle(ajdusted cell means) ///
name(prog_by_female, replace)
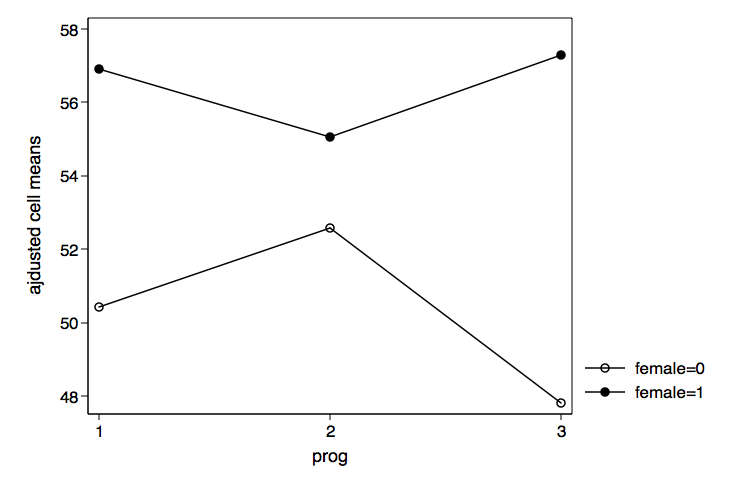
We can also graph the results for female by prog just by reversing c1 and c2 in the graph twoway command.
/* plot female by prog */
graph twoway (connect c3 c2 if c1==1)(connect c3 c2 if c1==2) ///
(connect c3 c2 if c1==3), xlabel(0 1) ///
legend(order(1 "prog=1" 2 "prog=2" 3 "prog=3")) ///
xtitle(female) ytitle(ajdusted cell means) ///
name(female_by_prog, replace)
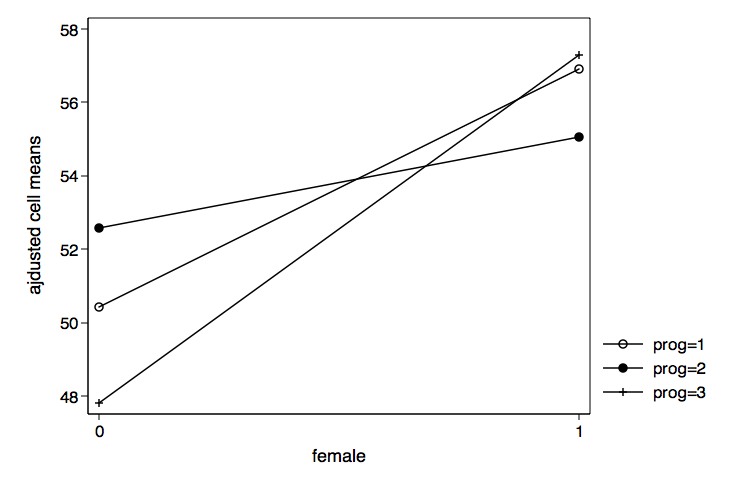
Example 2
For our second example we will graph the results of a categorical by continuous interaction from a logistic regression model.
use https://stats.idre.ucla.edu/stat/data/logitcatcon, clear
logit y i.f##c.s, nolog
Logistic regression Number of obs = 200
LR chi2(3) = 71.01
Prob > chi2 = 0.0000
Log likelihood = -96.28586 Pseudo R2 = 0.2694
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.f | 5.786811 2.302518 2.51 0.012 1.273959 10.29966
s | .1773383 .0364362 4.87 0.000 .1059248 .2487519
|
f#c.s |
1 | -.0895522 .0439158 -2.04 0.041 -.1756255 -.0034789
|
_cons | -9.253801 1.94189 -4.77 0.000 -13.05983 -5.447767
------------------------------------------------------------------------------
We will use the margins command to get the predicted probabilites for 11 values of s from 20 to 70 for both f equal zero and f equal one. The vsquish option just reduces the number of blank lines in the output.
margins f, at(s=(20(5)70)) vsquish
Adjusted predictions Number of obs = 200
Model VCE : OIM
Expression : Pr(y), predict()
1._at : s = 20
2._at : s = 25
3._at : s = 30
4._at : s = 35
5._at : s = 40
6._at : s = 45
7._at : s = 50
8._at : s = 55
9._at : s = 60
10._at : s = 65
11._at : s = 70
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at#f |
1 0 | .0033115 .0040428 0.82 0.413 -.0046123 .0112353
1 1 | .1529993 .098668 1.55 0.121 -.0403864 .3463851
2 0 | .0079995 .0083179 0.96 0.336 -.0083033 .0243023
2 1 | .2188574 .1104097 1.98 0.047 .0024583 .4352564
3 0 | .0191964 .0164503 1.17 0.243 -.0130456 .0514383
3 1 | .3029251 .1126363 2.69 0.007 .082162 .5236882
4 0 | .0453489 .0304422 1.49 0.136 -.0143166 .1050145
4 1 | .4026401 .1026147 3.92 0.000 .201519 .6037612
5 0 | .1033756 .0500784 2.06 0.039 .0052238 .2015275
5 1 | .5111116 .0827069 6.18 0.000 .349009 .6732142
6 0 | .2186457 .0674192 3.24 0.001 .0865065 .3507849
6 1 | .6185467 .0611384 10.12 0.000 .4987176 .7383758
7 0 | .4044675 .0706157 5.73 0.000 .2660634 .5428717
7 1 | .7155135 .0476424 15.02 0.000 .6221361 .8088909
8 0 | .622414 .0675171 9.22 0.000 .4900828 .7547452
8 1 | .795962 .0437198 18.21 0.000 .7102727 .8816513
9 0 | .8000327 .0610245 13.11 0.000 .6804269 .9196385
9 1 | .8581703 .0421992 20.34 0.000 .7754613 .9408793
10 0 | .9066322 .0443791 20.43 0.000 .8196508 .9936136
10 1 | .9037067 .0387213 23.34 0.000 .8278143 .9795991
11 0 | .9592963 .0267857 35.81 0.000 .9067973 1.011795
11 1 | .9357181 .0332641 28.13 0.000 .8705218 1.000914
------------------------------------------------------------------------------
In total, there are 22 values in the r(b) matrix. Once again we will put these values into a matrix called b.
matrix b=r(b)'
matrix list b
b[22,1]
r1
1._at#0.f .00331151
1._at#1.f .15299932
2._at#0.f .00799952
2._at#1.f .21885736
3._at#0.f .01919637
3._at#1.f .30292513
4._at#0.f .04534893
4._at#1.f .4026401
5._at#0.f .10337563
5._at#1.f .51111162
6._at#0.f .21864569
6._at#1.f .6185467
7._at#0.f .40446752
7._at#1.f .71551351
8._at#0.f .622414
8._at#1.f .79596199
9._at#0.f .8000327
9._at#1.f .85817031
10._at#0.f .9066322
10._at#1.f .9037067
11._at#0.f .95929634
11._at#1.f .93571812
Next, we need the 11 values of read found in the r(at) matrix. However, r(at) is an 11×3 matrix for which we only need the column labeled s. We also need to have two of each of the values of read which we will get by again using the Kronecker product.
matrix at=r(at)
matrix list at
at[11,3]
0b. 1.
f f s
r1 . . 20
r2 . . 25
r3 . . 30
r4 . . 35
r5 . . 40
r6 . . 45
r7 . . 50
r8 . . 55
r9 . . 60
r10 . . 65
r11 . . 70
matrix at=at[1...,"s"]#(11) /* # is the kronecker operator */
matrix list at
at[22,1]
s:
c1
r1:r1 20
r1:r2 20
r2:r3 25
r2:r4 25
r3:r5 30
r3:r6 30
r4:r7 35
r4:r8 35
r5:r9 40
r5:r10 40
r6:r11 45
r6:r12 45
r7:r13 50
r7:r14 50
r8:r15 55
r8:r16 55
r9:r17 60
r9:r18 60
r10:r19 65
r10:r20 65
r11:r21 70
r11:r22 70
We will put the at and b matrices together into matrix p and save the values to data. In this case it is easier to create the alternating series of 0’s and 1’s once the data are in memory using the line number modulo 2 with the not prefix so that the series starts with zero.
matrix p=at,b
matrix list p
p[22,2]
s:
c1 r1
r1:r1 20 .00331151
r1:r2 20 .15299932
r2:r3 25 .00799952
r2:r4 25 .21885736
r3:r5 30 .01919637
r3:r6 30 .30292513
r4:r7 35 .04534893
r4:r8 35 .4026401
r5:r9 40 .10337563
r5:r10 40 .51111162
r6:r11 45 .21864569
r6:r12 45 .6185467
r7:r13 50 .40446752
r7:r14 50 .71551351
r8:r15 55 .622414
r8:r16 55 .79596199
r9:r17 60 .8000327
r9:r18 60 .85817031
r10:r19 65 .9066322
r10:r20 65 .9037067
r11:r21 70 .95929634
r11:r22 70 .93571812
svmat p, names(p)
generate p3 = ~mod(_n,2) in 1/22
clist p1-p3 in 1/23
p1 p2 p3
1. 20 .0033115 0
2. 20 .1529993 1
3. 25 .0079995 0
4. 25 .2188574 1
5. 30 .0191964 0
6. 30 .3029251 1
7. 35 .0453489 0
8. 35 .4026401 1
9. 40 .1033756 0
10. 40 .5111116 1
11. 45 .2186457 0
12. 45 .6185467 1
13. 50 .4044675 0
14. 50 .7155135 1
15. 55 .622414 0
16. 55 .795962 1
17. 60 .8000327 0
18. 60 .8581703 1
19. 65 .9066322 0
20. 65 .9037067 1
21. 70 .9592963 0
22. 70 .9357181 1
23. . . .
Now we can go ahead and graph the probabilities for f equal zero and f equal one using the graph twoway command.
graph twoway (line p2 p1 if p3==0)(line p2 p1 if p3==1), ///
legend(order(1 "f=0" 2 "f=1")) xtitle(variable s) ///
ytitle(probability) name(probability, replace)
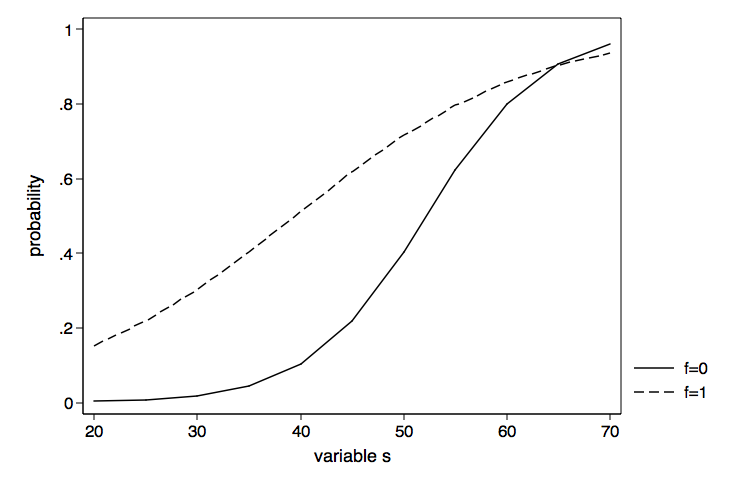
The graph of the probabilities above is nice as far as it goes but the presentation of the results might be clearer if we were to graph the difference in probabilities between f equal zero and f equal one. To do this we will need to rerun the margins command computing the discrete change for f at each value of read. We can get the difference using the dydx (derivative) option.
margins, dydx(f) at(s=(20(5)70)) vsquish
Conditional marginal effects Number of obs = 200
Model VCE : OIM
Expression : Pr(y), predict()
dy/dx w.r.t. : 1.f
1._at : s = 20
2._at : s = 25
3._at : s = 30
4._at : s = 35
5._at : s = 40
6._at : s = 45
7._at : s = 50
8._at : s = 55
9._at : s = 60
10._at : s = 65
11._at : s = 70
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.f |
_at |
1 | .1496878 .0987508 1.52 0.130 -.0438602 .3432358
2 | .2108578 .1107226 1.90 0.057 -.0061545 .4278701
3 | .2837288 .1138312 2.49 0.013 .0606236 .5068339
4 | .3572912 .107035 3.34 0.001 .1475064 .567076
5 | .407736 .0966865 4.22 0.000 .2182339 .597238
6 | .399901 .0910124 4.39 0.000 .22152 .578282
7 | .311046 .0851843 3.65 0.000 .1440878 .4780042
8 | .173548 .0804362 2.16 0.031 .0158959 .3312001
9 | .0581376 .0741941 0.78 0.433 -.0872801 .2035553
10 | -.0029255 .0588969 -0.05 0.960 -.1183612 .1125102
11 | -.0235782 .042708 -0.55 0.581 -.1072843 .0601279
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
Once again we will need the r(b) and r(at) values. But, we need to be careful this time because of the way that margins parameterizes these estimates there are 11 zero’s in the r(b) matrix before the 11 point estimates of interest. We will need to drop all of the rows with zero values.
matrix b=r(b)'
matrix list b
b[22,1]
r1
0b.f:1._at 0
0b.f:2._at 0
0b.f:3._at 0
0b.f:4._at 0
0b.f:5._at 0
0b.f:6._at 0
0b.f:7._at 0
0b.f:8._at 0
0b.f:9._at 0
0b.f:10._at 0
0b.f:11._at 0
1.f:1._at .14968781
1.f:2._at .21085784
1.f:3._at .28372876
1.f:4._at .35729117
1.f:5._at .40773598
1.f:6._at .399901
1.f:7._at .31104599
1.f:8._at .17354799
1.f:9._at .05813761
1.f:10._at -.00292551
1.f:11._at -.02357822
matrix b=b[12...,1]
matrix list b
b[11,1]
r1
1.f:1._at .14968781
1.f:2._at .21085784
1.f:3._at .28372876
1.f:4._at .35729117
1.f:5._at .40773598
1.f:6._at .399901
1.f:7._at .31104599
1.f:8._at .17354799
1.f:9._at .05813761
1.f:10._at -.00292551
1.f:11._at -.02357822
matrix at=r(at)
matrix at=at[1...,"s"]
matrix list at
at[11,1]
s
r1 20
r2 25
r3 30
r4 35
r5 40
r6 45
r7 50
r8 55
r9 60
r10 65
r11 70
For this graph of the differences in probabilities we will also include the lines for the 95% confidence interval. We will need to compute the upper and lower confidence values manually. To do this we will need the standard errors from the margins command. We will begin by getting the variance-covariance matrix of the estimates. Once again we will have to drop all of the rows and columns that are all zeros.
matrix v=r(V)
matrix v=v[12...,12...]
matrix list v
symmetric v[11,11]
1.f: 1.f: 1.f: 1.f: 1.f: 1.f: 1.f: 1.f:
1. 2. 3. 4. 5. 6. 7. 8.
_at _at _at _at _at _at _at _at
1.f:1._at .00975172
1.f:2._at .01090899 .01225949
1.f:3._at .01106858 .01252966 .01295755
1.f:4._at .00988489 .01133267 .01196523 .0114565
1.f:5._at .00746032 .00876206 .00961621 .00982147 .00934828
1.f:6._at .00437948 .00540815 .00638981 .00727808 .00804735 .00828325
1.f:7._at .00138994 .00201386 .00284747 .0039552 .0053869 .00685686 .00725637
1.f:8._at -.00090133 -.00072541 -.00028361 .00050889 .00177443 .00364155 .00568431 .00646999
1.f:9._at -.00219008 -.00231219 -.00218045 -.00173163 -.00085595 .00078305 .0033247 .00541876
1.f:10._at -.00260473 -.00282965 -.00279956 -.00246344 -.00177185 -.00047237 .00167411 .00372089
1.f:11._at -.00249143 -.00271383 -.00268483 -.00235557 -.00172561 -.00069732 .00085579 .00235456
1.f: 1.f: 1.f:
9. 10. 11.
_at _at _at
1.f:9._at .00550476
1.f:10._at .00422715 .00346884
1.f:11._at .00284913 .00245636 .00182397
The standard errors are found by taking the square roots of the digonal values of v. This actually invloves a series of steps; getting the diagonal values (vecdiag), putting them into a diagonal matrix (diag), getting the square roots (cholesky) and finally putting the values into a column vector (vecdiag). The one step that may not have been obvious is using the Cholesky decompostion on a diagonal matrix which gives us the square roots of the diagonal values. These four matrix functions are included in a single command shown below.
matrix se=vecdiag(cholesky(diag(vecdiag(v))))'
matrix list se
se[11,1]
r1
1.f:1._at .09875081
1.f:2._at .1107226
1.f:3._at .11383123
1.f:4._at .10703502
1.f:5._at .0966865
1.f:6._at .09101237
1.f:7._at .08518432
1.f:8._at .08043624
1.f:9._at .07419408
1.f:10._at .05889686
1.f:11._at .04270799
Next, we will put the at, b and se matrices together into matrix d and save them to the data in memory. Now we can generate the values for the upper and lower 95% confidence intervals.
matrix d=at,b,se
matrix list d
d[11,3]
s r1 r1
r1 20 .14968781 .09875081
r2 25 .21085784 .1107226
r3 30 .28372876 .11383123
r4 35 .35729117 .10703502
r5 40 .40773598 .0966865
r6 45 .399901 .09101237
r7 50 .31104599 .08518432
r8 55 .17354799 .08043624
r9 60 .05813761 .07419408
r10 65 -.00292551 .05889686
r11 70 -.02357822 .04270799
svmat d, names(d)
generate ul = d2 + 1.96*d3
generate ll = d2 - 1.96*d3
clist d1-ll in 1/12
d1 d2 d3 ul ll
1. 20 .1496878 .0987508 .3432394 -.0438638
2. 25 .2108578 .1107226 .4278741 -.0061585
3. 30 .2837287 .1138312 .506838 .0606195
4. 35 .3572912 .107035 .5670798 .1475025
5. 40 .407736 .0966865 .5972415 .2182304
6. 45 .399901 .0910124 .5782852 .2215168
7. 50 .311046 .0851843 .4780073 .1440847
8. 55 .173548 .0804362 .331203 .015893
9. 60 .0581376 .0741941 .203558 -.0872828
10. 65 -.0029255 .0588969 .1125123 -.1183634
11. 70 -.0235782 .042708 .0601294 -.1072859
12. . . . . .
Here is the graph twoway command to plot the differeces in probability with lines for the upper and lower confidence intervals.
graph twoway (line d2 ul ll d1), yline(0) legend(off) ///
xtitle(variable s) ytitle(difference in probability) ///
name(difference1, replace)
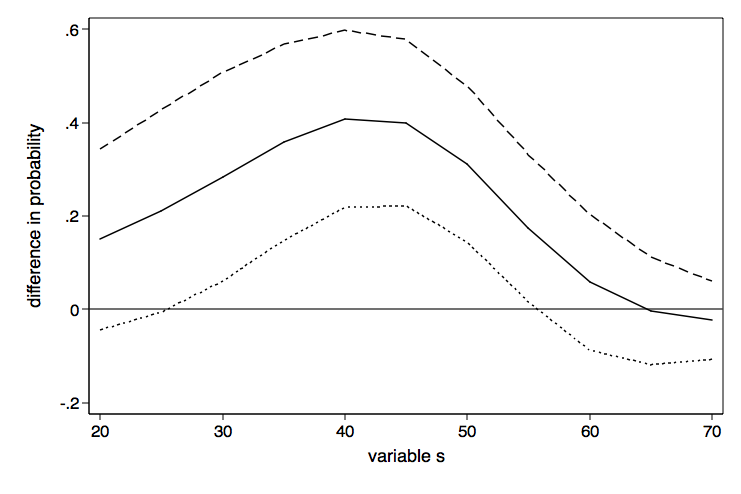
As nice as the above graph is, it might look better done as a range plot with area shading between the upper and lower confidence bounds.
graph twoway (rarea ul ll d1, color(gs13) lcolor(gs13)) ///
(line d2 d1), yline(0) legend(off) ///
xtitle(variable s) ytitle(difference in probability) ///
name(difference2, replace)
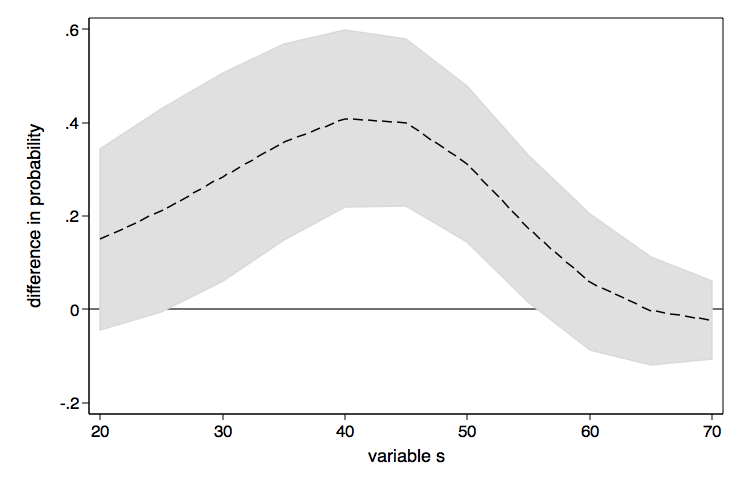
If you want the lines in these graphs to be smoother, just include more values in the at option, say (20(2)70) instead of (20(5)70).
Below you will find all of the code from both examples without the commentary.
/* example 1 -- plot adjusted cell means */
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
anova write prog##female math read
margins prog#female, asbalanced
mat b=r(b)'
mat prg=(123)#(11)
mat fem=(111)#(01)
mat c=prg,fem,b
svmat c, names(c)
/* plot prog by female */
graph twoway (connect c3 c1 if c2==0)(connect c3 c1 if c2==1), ///
xlabel(1 2 3) legend(order(1 "female=0" 2 "female=1")) ///
xtitle(prog) ytitle(ajdusted cell means) ///
name(prog_by_female, replace)
/* plot female by prog */
graph twoway (connect c3 c2 if c1==1)(connect c3 c2 if c1==2)(connect c3 c2 if c1==3), ///
xlabel(0 1) legend(order(1 "prog=1" 2 "prog=2" 3 "prog=3")) ///
xtitle(female) ytitle(ajdusted cell means) ///
name(female_by_prog, replace)
/* example 2 -- categorical by continuous */
use https://stats.idre.ucla.edu/stat/data/logitcatcon, clear
logit y i.f##c.s, nolog
/* plot probabilities by categorical variable */
margins f, at(s=(20(5)70)) vsquish
mat b=r(b)'
mat at=r(at)
mat at=at[1...,3]#(11)
mat p=at,b
svmat p, names(p)
generate p3 = ~mod(_n,2) in 1/52
graph twoway (line p2 p1 if p3==0)(line p2 p1 if p3==1), ///
legend(order(1 "f=0" 2 "f=1")) xtitle(variable s) ///
ytitle(probability) name(probability, replace)
/* difference in probabilities */
margins, dydx(f) at(s=(20(5)70)) vsquish
mat b=r(b)'
mat at=r(at)
mat at=at[1...,3]
local nrow=rowsof(at)
mat b=b[`nrow'+1...,1]
mat se=r(V)
mat se=se[`nrow'+1...,`nrow'+1...]
mat se=vecdiag(cholesky(diag(vecdiag(se))))'
mat d=at,b,se
mat lis d
svmat d, names(d)
gen ul = d2 + 1.96*d3
gen ll = d2 - 1.96*d3
graph twoway (line d2 ul ll d1), yline(0) legend(off) ///
xtitle(variable s) ytitle(difference in probability) ///
name(difference1, replace)
graph twoway (rarea ul ll d1, color(gs13) lcolor(gs13)) ///
(line d2 d1), yline(0) legend(off) ///
xtitle(variable s) ytitle(difference in probability) ///
name(difference2, replace)
