The web page, How can I use the margins command to understand multiple interactions in regression and anova?, presented two examples of models with multiple interactions involving categorical variables. We have recently received a question concerning models with multiple continuous by continuous interactions. As on the previous page we will use the margins command (new in Stata 11) to assist our understanding model. We will illustrate the process using the hsbdemo dataset.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
We will use a model that has two continuous by continuous interactions (math by socst) and (math by science). You will note that the two interactions have a common variable, math. Just for the record, the three-way interaction (math by socst by science), is not significant and will, therefore, not be included in our model. We will begin by running our model using both anova and regress.
anova read c.math c.socst c.science c.math#c.socst c.math#c.science
Number of obs = 200 R-squared = 0.6047
Root MSE = 6.52878 Adj R-squared = 0.5945
Source | Partial SS df MS F Prob > F
-------------+----------------------------------------------------
Model | 12650.1861 5 2530.03721 59.36 0.0000
|
math | 1.30895916 1 1.30895916 0.03 0.8611
socst | 192.889679 1 192.889679 4.53 0.0347
science | 377.039608 1 377.039608 8.85 0.0033
math#socst | 433.477441 1 433.477441 10.17 0.0017
math#science | 184.101663 1 184.101663 4.32 0.0390
|
Residual | 8269.23395 194 42.6249173
-------------+----------------------------------------------------
Total | 20919.42 199 105.122714
regress read math socst science c.math#c.socst c.math#c.science
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 5, 194) = 59.36
Model | 12650.1861 5 2530.03721 Prob > F = 0.0000
Residual | 8269.23395 194 42.6249173 R-squared = 0.6047
-------------+------------------------------ Adj R-squared = 0.5945
Total | 20919.42 199 105.122714 Root MSE = 6.5288
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math | .0584261 .3334076 0.18 0.861 -.5991428 .715995
socst | -.6400056 .3008577 -2.13 0.035 -1.233377 -.0466338
science | .9663902 .3249307 2.97 0.003 .3255398 1.607241
|
c.math#|
c.socst | .0183854 .0057653 3.19 0.002 .0070147 .0297561
|
c.math#|
c.science | -.0131131 .0063097 -2.08 0.039 -.0255576 -.0006687
|
_cons | 17.41922 16.29963 1.07 0.287 -14.72801 49.56644
------------------------------------------------------------------------------
As you can see the math#socst and math#science interactions are significant, as are the one degree of freedom tests for socst and science. Let’s begin by looking at the regression of read on math for five different values of socst while holding science at the value 40 (about one standard deviation below the mean). We will compute the simple slopes and the interactions so that we can plot the results. We get the intercepts by setting the variable of interest (math) to zero in the margins command.
/* simple slopes */
margins, dydx(math) at(socst=(30(10)70) science=40)
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
1._at : socst = 30
science = 40
2._at : socst = 40
science = 40
3._at : socst = 50
science = 40
4._at : socst = 60
science = 40
5._at : socst = 70
science = 40
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | .0854634 .1412188 0.61 0.545 -.1913204 .3622472
2 | .2693175 .1131738 2.38 0.017 .047501 .4911341
3 | .4531717 .1110027 4.08 0.000 .2356104 .6707329
4 | .6370258 .1359508 4.69 0.000 .3705671 .9034845
5 | .8208799 .1768937 4.64 0.000 .4741746 1.167585
------------------------------------------------------------------------------
matrix s=r(b) /* capture slopes for graphing */
/* intercepts for simple slopes */
margins, at(math=0 socst=(30(10)70) science=40)
Adjusted predictions Number of obs = 200
Expression : Linear prediction, predict()
1._at : math = 0
socst = 30
science = 40
2._at : math = 0
socst = 40
science = 40
3._at : math = 0
socst = 50
science = 40
4._at : math = 0
socst = 60
science = 40
5._at : math = 0
socst = 70
science = 40
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | 36.87466 6.687053 5.51 0.000 23.76827 49.98104
2 | 30.4746 5.234331 5.82 0.000 20.2155 40.7337
3 | 24.07454 5.30875 4.53 0.000 13.66958 34.4795
4 | 17.67449 6.860795 2.58 0.010 4.227576 31.1214
5 | 11.27443 9.168492 1.23 0.219 -6.695484 29.24434
------------------------------------------------------------------------------
matrix i=r(b) /* capture intercepts for graphing */
/* let's graph it */
graph twoway (function y = i[1,1]+s[1,1]*x, range(30 70)) ///
(function y = i[1,2]+s[1,2]*x, range(30 70)) ///
(function y = i[1,3]+s[1,3]*x, range(30 70)) ///
(function y = i[1,4]+s[1,4]*x, range(30 70)) ///
(function y = i[1,5]+s[1,5]*x, range(30 70)), ///
legend(order(1 "socst=30" 2 "socst=40" ///
3 "socst=50" 4 "socst=60" 5 "socst=70")) ///
xtitle(math) ytitle(write) scheme(lean1) ///
title(Simple slopes with science at 40)
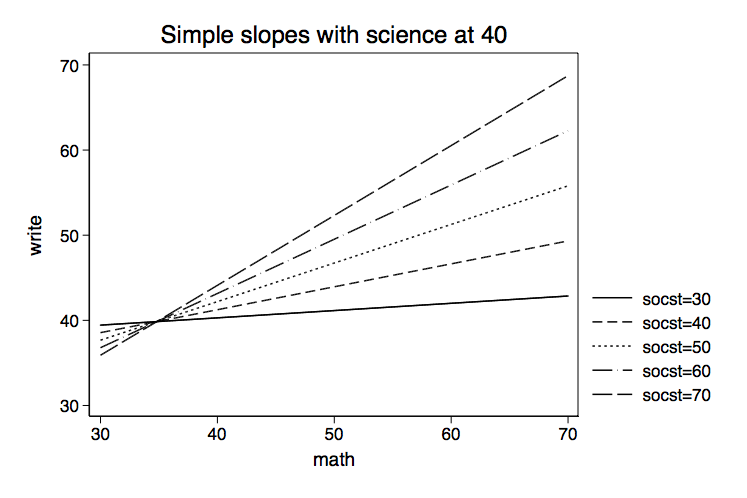
We could repeat the process setting science at 50 and then 60. Then we could plot write on math with science at 5 different values and socst at 30, 40, 50, 60 and 70. We will go ahead and run the margins command for the simple slopes, but we will not compute the intercepts or create the graphs. Rather, we will look at how the slopes change for the different values of socst and science. We will start with the simple slopes for the math by socst interaction and we will repeat the first analysis for comparison purposes.
margins, dydx(math) at(socst=(30(10)70) science=40) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | .0854634 .1412188 0.61 0.545 -.1913204 .3622472
2 | .2693175 .1131738 2.38 0.017 .047501 .4911341
3 | .4531717 .1110027 4.08 0.000 .2356104 .6707329
4 | .6370258 .1359508 4.69 0.000 .3705671 .9034845
5 | .8208799 .1768937 4.64 0.000 .4741746 1.167585
------------------------------------------------------------------------------
margins, dydx(math) at(socst=(30(10)70) science=50) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | -.0456679 .1446235 -0.32 0.752 -.3291248 .237789
2 | .1381863 .0998225 1.38 0.166 -.0574622 .3338347
3 | .3220404 .0752385 4.28 0.000 .1745757 .4695051
4 | .5058945 .0894699 5.65 0.000 .3305367 .6812524
5 | .6897487 .1303712 5.29 0.000 .4342259 .9452715
------------------------------------------------------------------------------
margins, dydx(math) at(socst=(30(10)70) science=60) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | -.1767991 .1727763 -1.02 0.306 -.5154345 .1618362
2 | .007055 .1228138 0.06 0.954 -.2336556 .2477656
3 | .1909091 .0834418 2.29 0.022 .0273661 .3544521
4 | .3747633 .0740918 5.06 0.000 .2295461 .5199805
5 | .5586174 .1032685 5.41 0.000 .3562149 .7610199
------------------------------------------------------------------------------
As you can see, for each of the values of science the simple slopes increase as the values of socst increase. Next, we will repeat the process focusing on the simple slopes for the math by science interaction holding socst at five values.
margins, dydx(math) at(science=(30(10)70) socst=40) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | .4004488 .1536703 2.61 0.009 .0992605 .7016371
2 | .2693175 .1131738 2.38 0.017 .047501 .4911341
3 | .1381863 .0998225 1.38 0.166 -.0574622 .3338347
4 | .007055 .1228138 0.06 0.954 -.2336556 .2477656
5 | -.1240763 .1678225 -0.74 0.460 -.4530024 .2048499
------------------------------------------------------------------------------
margins, dydx(math) at(science=(30(10)70) socst=50) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | .5843029 .1641489 3.56 0.000 .2625771 .9060288
2 | .4531717 .1110027 4.08 0.000 .2356104 .6707329
3 | .3220404 .0752385 4.28 0.000 .1745757 .4695051
4 | .1909091 .0834418 2.29 0.022 .0273661 .3544521
5 | .0597779 .1273842 0.47 0.639 -.1898905 .3094463
------------------------------------------------------------------------------
margins, dydx(math) at(science=(30(10)70) socst=60) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | .7681571 .1921532 4.00 0.000 .3915437 1.14477
2 | .6370258 .1359508 4.69 0.000 .3705671 .9034845
3 | .5058945 .0894699 5.65 0.000 .3305367 .6812524
4 | .3747633 .0740918 5.06 0.000 .2295461 .5199805
5 | .243632 .1045791 2.33 0.020 .0386607 .4486033
------------------------------------------------------------------------------
This time the simple slopes decrease as the moderator (science) increases for each of the values of socst.
While not exhaustive, this analysis is fairly complete. It is also possible to use a somewhat simpler analysis in which the third variable is held constant at its mean value. The results lead to similar conclusions as is shown below.
/* simple slope for math#socst interaction with science held at its mean value */
margins, dydx(math) at(socst=(30(10)70) (mean) science) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | -.0699271 .1482187 -0.47 0.637 -.3604305 .2205762
2 | .113927 .1015441 1.12 0.262 -.0850959 .3129499
3 | .2977811 .0728105 4.09 0.000 .1550751 .4404872
4 | .4816353 .0833023 5.78 0.000 .3183658 .6449047
5 | .6654894 .1233892 5.39 0.000 .4236509 .9073279
------------------------------------------------------------------------------
/* simple slope for math#science interaction with socst held at its mean value */
margins, dydx(math) at(science=(30(10)70) (mean) socst) noatlegend
Average marginal effects Number of obs = 200
Expression : Linear prediction, predict()
dy/dx w.r.t. : math
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
math |
_at |
1 | .6285198 .1695212 3.71 0.000 .2962645 .9607752
2 | .4973886 .1148747 4.33 0.000 .2722384 .7225388
3 | .3662573 .0749495 4.89 0.000 .2193589 .5131557
4 | .235126 .0774671 3.04 0.002 .0832932 .3869588
5 | .1039948 .1197805 0.87 0.385 -.1307707 .3387602
------------------------------------------------------------------------------
As you can no doubt tell, the process can get rather complex. So, even though there was no three-way interaction, the process we have gone through is very similar to that used for significant three-way continuous by continuous interactions.
