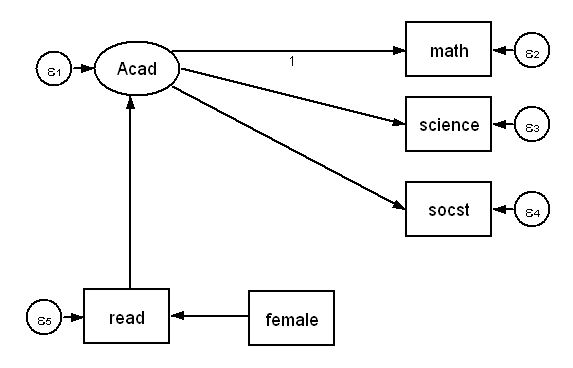
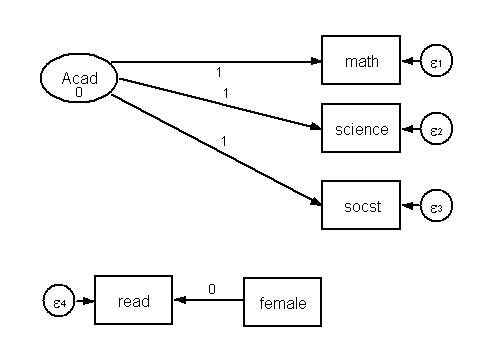
Below is the diagram of a simple structural equation model. The dependent variable is a latent variable Acad with three observed indicators, math, science and socst. There are two additional observed variables, the independent variable female and a mediator variable read. (Note, variables in squares are observed (manifest variables), those in circles are latent. The small circles with ε are error terms, i.e., residual variances).
We will analyze this model using the sem command with the hsbdemo dataset.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
sem (Acad->math science socst)(Acad<-read)(read<-female), ///
mean(female) var(female)
Endogenous variables
Observed: read
Measurement: math science socst
Latent: Acad
Exogenous variables
Observed: female
Fitting target model:
Iteration 0: log likelihood = -6737.783 (not concave)
[output omitted]
Iteration 13: log likelihood = -2949.3343
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -2949.3343
( 1) [math]Acad = 1
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
read <- |
female | -1.090231 1.450201 -0.75 0.452 -3.932572 1.75211
_cons | 52.82418 1.070598 49.34 0.000 50.72584 54.92251
-----------+----------------------------------------------------------------
Acad <- |
read | .620298 .0461021 13.45 0.000 .5299395 .7106565
-------------+----------------------------------------------------------------
Measurement |
math <- |
Acad | 1 (constrained)
_cons | 20.24684 2.456312 8.24 0.000 15.43255 25.06112
-----------+----------------------------------------------------------------
science <- |
Acad | .9874351 .0908878 10.86 0.000 .8092984 1.165572
_cons | 19.85891 2.737663 7.25 0.000 14.49319 25.22463
-----------+----------------------------------------------------------------
socst <- |
Acad | .9940776 .1030617 9.65 0.000 .7920804 1.196075
_cons | 20.19871 3.181537 6.35 0.000 13.96301 26.4344
-------------+----------------------------------------------------------------
Mean |
female | .545 .0352119 15.48 0.000 .475986 .614014
-------------+----------------------------------------------------------------
Variance |
e.math | 31.77659 4.630872 23.8814 42.28192
e.science | 43.37236 5.487556 33.84678 55.57874
e.socst | 59.7846 7.011562 47.50727 75.23477
e.read | 104.3024 10.43024 85.73812 126.8862
e.Acad | 15.30659 3.693936 9.538023 24.56398
female | .247975 .0247975 .2038392 .3016672
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(5) = 12.25, Prob > chi2 = 0.0315
estat gof
----------------------------------------------------------------------------
Fit statistic | Value Description
---------------------+------------------------------------------------------
Likelihood ratio |
chi2_ms(5) | 12.251 model vs. saturated
p > chi2 | 0.032
chi2_bs(10) | 361.012 baseline vs. saturated
p > chi2 | 0.000
----------------------------------------------------------------------------
The estat gof makes reference to three different models; 1) the model (the one we just ran), 2) the saturated model, and 3) the baseline model. Before we discuss the saturated and baseline models, let’s look a little closer at the above model.
In the above model we estimated 15 parameters; 2 structural coefficients, 1 structural intercept, 2 measurement coefficients (loadings), 3 measurement intercepts, 6 variances and 1 mean. The log likelihood for our model was -2949.3343.
The saturated model
Now let’s move on to the saturated model. A saturated model perfectly reproduces all of the variances, covariance and means of the observed variables. Here is a simple way to produce a saturated model.
sem (<-read math science socst female)
Exogenous variables
Observed: read math science socst female
Fitting target model:
Iteration 0: log likelihood = -2943.2087
Iteration 1: log likelihood = -2943.2087
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -2943.2087
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Mean |
read | 52.23 .7231774 72.22 0.000 50.8126 53.6474
math | 52.645 .6607911 79.67 0.000 51.34987 53.94013
science | 51.85 .6983463 74.25 0.000 50.48127 53.21873
socst | 52.405 .757235 69.21 0.000 50.92085 53.88915
female | .545 .0352119 15.48 0.000 .475986 .614014
-------------+----------------------------------------------------------------
Variance |
read | 104.5971 10.45971 85.98041 127.2447
math | 87.32898 8.732897 71.78574 106.2377
science | 97.5375 9.75375 80.17731 118.6566
socst | 114.681 11.4681 94.2695 139.512
female | .247975 .0247975 .2038392 .3016672
-------------+----------------------------------------------------------------
Covariance |
read |
math | 63.29665 8.105808 7.81 0.000 47.40956 79.18374
science | 63.6495 8.441978 7.54 0.000 47.10353 80.19547
socst | 68.06685 9.118222 7.46 0.000 50.19546 85.93824
female | -.27035 .3606283 -0.75 0.453 -.9771685 .4364685
-----------+----------------------------------------------------------------
math |
science | 58.21175 7.715717 7.54 0.000 43.08922 73.33428
socst | 54.48877 8.057294 6.76 0.000 38.69677 70.28078
female | -.136525 .3291963 -0.41 0.678 -.7817379 .5086879
-----------+----------------------------------------------------------------
science |
socst | 49.19075 8.247856 5.96 0.000 33.02525 65.35625
female | -.62825 .3505821 -1.79 0.073 -1.315378 .0588783
-----------+----------------------------------------------------------------
socst |
female | .279275 .3775977 0.74 0.460 -.460803 1.019353
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
A saturated model has the best fit possible since it perfectly reproduces all of the variances, covariances and means. That’s why the saturated model above has a chi-square of zero with zero degrees of freedom. Since you can’t do any better than a saturated model, it becomes the standard for comparison with the models that you estimate.
For the saturated model we estimated 20 parameters; 5 variances, 10 covariances and 5 means. You can compute the number of parameters in a saturated model of k observed variables by the formula k*(k+1)/2 + k. In our example, it is 5*(5+1)/2 + 5 = 20. The log likelihood for this model is -2943.2087.
To test how well our model compares to a saturated model, we compute chi-square as follows, minus two times the differences in the log likelihoods; -2*(-2949.3343 – -2943.2087) = 12.2512. The degrees of freedom for this chi-square is the difference in the number of parameters estimated in the two model (20 – 15 = 5). Thus, our model fits significantly poorer than a saturated model (p = .0315). But, that’s not surprising since our model was only for demonstration purposes.
The baseline model
So, that brings us to the baseline model. This is defined in the Stata [SEM] Structural Equation Modeling Reference Manual as a model which includes the means and variances of all observed variables plus the covariances of all observed exogenous variables. Since there is only one observed exogenous variable, female, in our model, there will be no covariances in our baseline model.
sem (<-read math science socst female), ///
covstr(read math science socst female, diagonal)
Exogenous variables
Observed: read math science socst female
Fitting target model:
Iteration 0: log likelihood = -3123.7147
Iteration 1: log likelihood = -3123.7147
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -3123.7147
( 1) [cov(read,math)]_cons = 0
( 2) [cov(read,science)]_cons = 0
( 3) [cov(read,socst)]_cons = 0
( 4) [cov(read,female)]_cons = 0
( 5) [cov(math,science)]_cons = 0
( 6) [cov(math,socst)]_cons = 0
( 7) [cov(math,female)]_cons = 0
( 8) [cov(science,socst)]_cons = 0
( 9) [cov(science,female)]_cons = 0
(10) [cov(socst,female)]_cons = 0
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Mean |
read | 52.23 .7231774 72.22 0.000 50.8126 53.6474
math | 52.645 .6607911 79.67 0.000 51.34987 53.94013
science | 51.85 .6983463 74.25 0.000 50.48127 53.21873
socst | 52.405 .757235 69.21 0.000 50.92085 53.88915
female | .545 .0352119 15.48 0.000 .475986 .614014
-------------+----------------------------------------------------------------
Variance |
read | 104.5971 10.45971 85.98041 127.2447
math | 87.32898 8.732898 71.78574 106.2377
science | 97.5375 9.75375 80.17731 118.6566
socst | 114.681 11.4681 94.2695 139.512
female | .247975 .0247975 .2038392 .3016672
-------------+----------------------------------------------------------------
Covariance |
read |
math | 0 (constrained)
science | 0 (constrained)
socst | 0 (constrained)
female | 0 (constrained)
-----------+----------------------------------------------------------------
math |
science | 0 (constrained)
socst | 0 (constrained)
female | 0 (constrained)
-----------+----------------------------------------------------------------
science |
socst | 0 (constrained)
female | 0 (constrained)
-----------+----------------------------------------------------------------
socst |
female | 0 (constrained)
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(10) = 361.01, Prob > chi2 = 0.0000
For the baseline model we estimated 10 parameters; 5 variances and 5 means. In comparing this model with the saturated model there was a difference of 10 degrees of freedom, 20 – 10 = 10. Again, we compute chi-square as minus two times the difference in the log likelihoods, -2*(-3123.7147 – -2943.2087) = 361.012.
Although our model did not fit all that well compared to the saturated model, the fit of the baseline model compared to the saturated model is much worse, with chi2(10) = 361.012, p = 0.0000.
The two chi-square values from the estat gof for our model versus a saturated model and baseline versus saturated model help us to understand how well our model fits the data.
The saturated model revisited
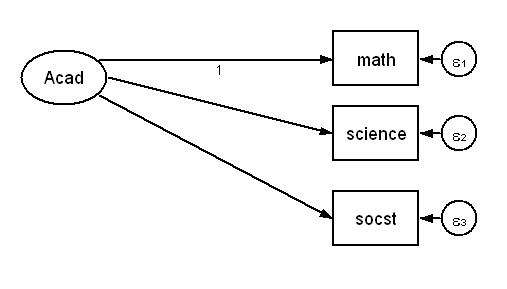
When we looked at the saturated model above we used a very simple model with only observed variables. Now we are going to try to come up with a saturated model that is more closely related to our original model. We will begin by looking at just the measurement part of our model. Here is the diagram.
Followed by the sem code.
sem (Acad->math science socst)
Endogenous variables
Measurement: math science socst
Exogenous variables
Latent: Acad
Fitting target model:
Iteration 0: log likelihood = -2141.1294
Iteration 1: log likelihood = -2141.1294
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -2141.1294
( 1) [math]Acad = 1
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Measurement |
math <- |
Acad | 1 (constrained)
_cons | 52.645 .6607911 79.67 0.000 51.34987 53.94013
-----------+----------------------------------------------------------------
science <- |
Acad | .9027685 .1108342 8.15 0.000 .6855374 1.12
_cons | 51.85 .6983463 74.25 0.000 50.48127 53.21873
-----------+----------------------------------------------------------------
socst <- |
Acad | .8450313 .110572 7.64 0.000 .6283142 1.061748
_cons | 52.405 .757235 69.21 0.000 50.92085 53.88915
-------------+----------------------------------------------------------------
Variance |
e.math | 22.84761 7.002427 12.53029 41.66011
e.science | 44.98577 7.024159 33.12585 61.09185
e.socst | 68.63626 8.333688 54.10062 87.07729
Acad | 64.48137 10.71715 46.55433 89.31172
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
As you can see, the measure model with three indicators is itself a saturated model. To be saturated it should have 3*4/2 + 3 = 9 parameters being estimated, which is the case.
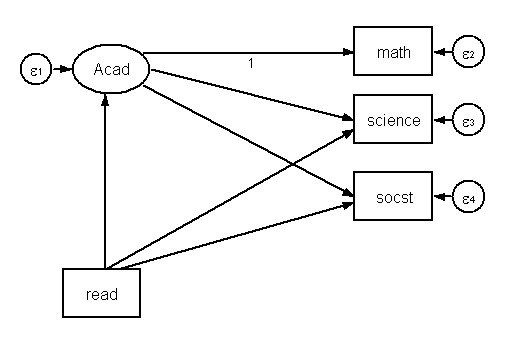
Now, let’s add read to our model like this.
sem (Acad->math science socst)(Acad<-read)(science<-read)(socst<-read), ///
mean(read) difficult
Endogenous variables
Observed: science socst
Measurement: math
Latent: Acad
Exogenous variables
Observed: read
Fitting target model:
Iteration 0: log likelihood = -3698.205 (not concave)
[output omitted]
Iteration 28: log likelihood = -2802.3352
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -2802.3352
( 1) [math]Acad = 1
-------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
--------------+----------------------------------------------------------------
Structural |
science <- |
Acad | .5843354 .3233183 1.81 0.071 -.0493567 1.218028
read | .2549117 .2019701 1.26 0.207 -.1409425 .6507659
_cons | 20.06696 2.821788 7.11 0.000 14.53636 25.59757
------------+----------------------------------------------------------------
socst <- |
Acad | .3945619 .2262457 1.74 0.081 -.0488715 .8379953
read | .4119847 .148232 2.78 0.005 .1214554 .702514
_cons | 18.41618 3.087163 5.97 0.000 12.36546 24.46691
------------+----------------------------------------------------------------
Acad <- |
read | .6051473 .04841 12.50 0.000 .5102655 .700029
--------------+----------------------------------------------------------------
Measurement |
math <- |
Acad | 1 (constrained)
_cons | 21.03816 2.57647 8.17 0.000 15.98837 26.08795
--------------+----------------------------------------------------------------
mean(read)| 52.23 .7231774 72.22 0.000 50.8126 53.6474
--------------+----------------------------------------------------------------
var(e.math)| 15.32121 18.29777 1.474762 159.171
var(e.science)| 47.29731 7.818624 34.20787 65.39535
var(e.socst)| 65.13928 7.105546 52.60074 80.66665
var(e.Acad)| 33.70397 18.81883 11.28255 100.6827
var(read)| 104.5971 10.45971 85.98041 127.2447
-------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
This model has four observed variables. Thus, we should estimate 4*5/2 + 4 = 14 parameters. We achieved this by adding direct paths from read to science and to socst. We could have also achieved the same result by adding two covariances, say e.math*e.science and e.math*e.socst, to our model instead of the direct effects.
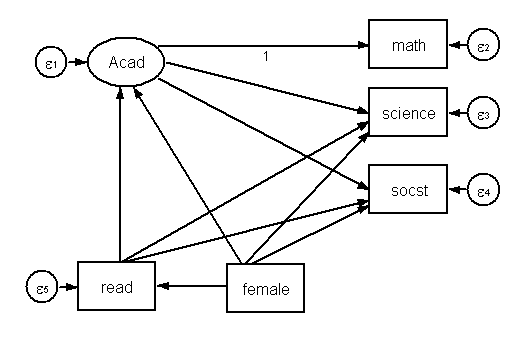
Finally, let’s add female to our model. We now have as many observed variables as our original model.
The above diagram translates to the following code.
sem (Acad -> math science socst)(Acad<-read)(Acad<-female)(read<-female) ///
(math<- female read)(socst<-female read), ///
mean(female) var(female)
Endogenous variables
Observed: math socst read
Measurement: science
Latent: Acad
Exogenous variables
Observed: female
Fitting target model:
Iteration 0: log likelihood = -3111.6647 (not concave)
[output omitted]
Iteration 58: log likelihood = -2943.2087
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -2943.2087
( 1) [math]Acad = 1
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
math <- |
read | -.3219013 .4660796 -0.69 0.490 -1.235401 .5915979
Acad | 1 (constrained)
female | 2.990358 2.137855 1.40 0.162 -1.199762 7.180477
_cons | 20.9637 2.663851 7.87 0.000 15.74265 26.18475
-----------+----------------------------------------------------------------
socst <- |
read | .250464 .1525691 1.64 0.101 -.0485661 .549494
Acad | .436786 .2230541 1.96 0.050 -.0003919 .8739639
female | 3.099202 1.37288 2.26 0.024 .4084072 5.789998
_cons | 17.16439 3.172945 5.41 0.000 10.94553 23.38325
-----------+----------------------------------------------------------------
read <- |
female | -1.090232 1.450201 -0.75 0.452 -3.932574 1.75211
_cons | 52.82418 1.070598 49.34 0.000 50.72584 54.92251
-----------+----------------------------------------------------------------
Acad <- |
read | .9273316 .4666623 1.99 0.047 .0126903 1.841973
female | -2.880859 2.192737 -1.31 0.189 -7.178543 1.416826
-------------+----------------------------------------------------------------
Measurement |
science <- |
Acad | .6509763 .3226734 2.02 0.044 .018548 1.283405
_cons | 21.34222 2.895969 7.37 0.000 15.66623 27.01822
-------------+----------------------------------------------------------------
Mean |
female | .545 .0352119 15.48 0.000 .475986 .614014
-------------+----------------------------------------------------------------
Variance |
e.math | 18.69062 14.85898 3.934787 88.78225
e.science | 45.08212 7.703921 32.25118 63.01778
e.socst | 63.76156 6.970891 51.46349 78.99847
e.read | 104.3024 10.43024 85.73812 126.8862
e.Acad | 30.33159 15.41889 11.19933 82.1483
female | .247975 .0247975 .2038392 .3016672
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
This time there are five observed variables which means that we need to estimate 5*6/2 + 5 = 20 parameters for a saturated model. We did this by adding direct paths from female to Acad, math, and socst and direct paths from read to math and socst. This is the same result that was obtained with the simpler approach used earlier for the saturated model.
The baseline model revisited
We know that the baseline model estimates five means and five variances and no covariances, because there is only one observed exogenous variables, for a total of 10 total parameters. We can get this from our original model by constraining all of the measurement coefficients (loadings) to be one and all of the path coefficients to be zero. Here is a diagram of the model.
And, here is one way to accomplish this.
sem (Acad ->math@1 science@1 socst@1) (read<-female@0), ///
var(Acad@0 female) mean(female)
Endogenous variables
Observed: read
Measurement: math science socst
Exogenous variables
Observed: female
Latent: Acad
Fitting target model:
Iteration 0: log likelihood = -3257.7854
[omitted output]
Iteration 4: log likelihood = -3123.7147
Structural equation model Number of obs = 200
Estimation method = ml
Log likelihood = -3123.7147
( 1) [math]Acad = 1
( 2) [science]Acad = 1
( 3) [socst]Acad = 1
( 4) [var(Acad)]_cons = 0
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Structural |
read <- |
_cons | 52.23 .7231774 72.22 0.000 50.8126 53.6474
-------------+----------------------------------------------------------------
Measurement |
math <- |
Acad | 1 (constrained)
_cons | 52.645 .6607909 79.67 0.000 51.34987 53.94013
-----------+----------------------------------------------------------------
science <- |
Acad | 1 (constrained)
_cons | 51.85 .6983462 74.25 0.000 50.48127 53.21873
-----------+----------------------------------------------------------------
socst <- |
Acad | 1 (constrained)
_cons | 52.405 .757235 69.21 0.000 50.92085 53.88915
-------------+----------------------------------------------------------------
Mean |
female | .545 .0352119 15.48 0.000 .475986 .614014
-------------+----------------------------------------------------------------
Variance |
e.math | 87.32893 8.732889 71.78572 106.2376
e.science | 97.53748 9.753746 80.17729 118.6565
e.socst | 114.681 11.4681 94.2695 139.512
e.read | 104.5971 10.45971 85.98041 127.2447
female | .247975 .0247975 .2038392 .3016672
Acad | 0 (constrained)
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(10) = 361.01, Prob > chi2 = 0.0000
In this model the term (read<-female@0) estimates an intercept (mean) but no structural coefficient. There is no term that predicting Acad from read which is equivalent to setting that structural coefficient to zero. We added terms for the mean and variance of female. Finally, by convention, the variance of the latent variables is constrained to zero, which we did.