Here is a traditional regression model with an interaction:
regress y x1 x2 x1#x2
We see two main effects (x1 & x2) in addition to the interaction term (x1#x2). Is it “legal” to omit one or both main effects? Is it really necessary to include both main effects when the interaction is present?
The simple answer is no, you don’t always need main effects when there is an interaction. However, the interaction term will not have the same meaning as it would if both main effects were included in the model.
We will explore regression models that include an interaction term but only one of two main effect terms using the hsbanova dataset.
use https://stats.idre.ucla.edu/stat/data/hsbanova, clear
Case 1: Categorical by categorical interaction
We will begin by looking at a model with two categorical main effects and an interaction. We will refer to this model as the “full” model.
regress write i.female##i.grp
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 11.05
Model | 5135.17494 7 733.59642 Prob > F = 0.0000
Residual | 12743.7001 192 66.3734378 R-squared = 0.2872
-------------+------------------------------ Adj R-squared = 0.2612
Total | 17878.875 199 89.843593 Root MSE = 8.147
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.female | 9.136876 2.311726 3.95 0.000 4.577236 13.69652
|
grp |
2 | 7.31677 2.458951 2.98 0.003 2.466743 12.1668
3 | 10.10248 2.292658 4.41 0.000 5.580454 14.62452
4 | 16.75286 2.525696 6.63 0.000 11.77119 21.73453
|
female#grp |
1 2 | -5.029733 3.357123 -1.50 0.136 -11.65131 1.591845
1 3 | -3.721697 3.128694 -1.19 0.236 -9.892723 2.449328
1 4 | -9.831208 3.374943 -2.91 0.004 -16.48793 -3.174482
|
_cons | 41.82609 1.698765 24.62 0.000 38.47545 45.17672
------------------------------------------------------------------------------
This model has an overall F of 11.05 with 7 and 192 degrees of freedom and has an R2 of .2827.
Example 1.1
Now, let’s run the model but leave female out of the regress command.
regress write i.grp i.female#i.grp
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 11.05
Model | 5135.17494 7 733.59642 Prob > F = 0.0000
Residual | 12743.7001 192 66.3734378 R-squared = 0.2872
-------------+------------------------------ Adj R-squared = 0.2612
Total | 17878.875 199 89.843593 Root MSE = 8.147
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
grp |
2 | 7.31677 2.458951 2.98 0.003 2.466743 12.1668
3 | 10.10248 2.292658 4.41 0.000 5.580454 14.62452
4 | 16.75286 2.525696 6.63 0.000 11.77119 21.73453
|
female#grp |
1 1 | 9.136876 2.311726 3.95 0.000 4.577236 13.69652
1 2 | 4.107143 2.434379 1.69 0.093 -.6944172 8.908703
1 3 | 5.415179 2.108234 2.57 0.011 1.256906 9.573452
1 4 | -.694332 2.458895 -0.28 0.778 -5.544247 4.155583
|
_cons | 41.82609 1.698765 24.62 0.000 38.47545 45.17672
------------------------------------------------------------------------------
This model has the same overall F, degrees of freedom and R2 as our “full” model. So, in fact, this is just a reparameterization of the “full” model. It contains all of the information from our first model but it is organized differently. This shows that Stata is smart about the missing main-effect and generated an “interaction” term with four degrees of freedom instead of three. Thus keeping the overall model degrees of freedom at seven.
In this case, the coefficients for the “interaction” are actually simple effects. For example, the first “interaction” coefficient is the simple effect of female at grp equal to one. It shows that there is a significant male/female difference for grp 1.
We could get the same four simple effects tests from the “full” regression model using the following Stata 12 code.
regress write i.grp i.female#i.grp contrast female@grp
Example 1.2
What if we ran the regression including just the main effect for female?
regress write i.female i.female#i.grp
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 11.05
Model | 5135.17494 7 733.59642 Prob > F = 0.0000
Residual | 12743.7001 192 66.3734378 R-squared = 0.2872
-------------+------------------------------ Adj R-squared = 0.2612
Total | 17878.875 199 89.843593 Root MSE = 8.147
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.female | 9.136876 2.311726 3.95 0.000 4.577236 13.69652
|
female#grp |
0 2 | 7.31677 2.458951 2.98 0.003 2.466743 12.1668
0 3 | 10.10248 2.292658 4.41 0.000 5.580454 14.62452
0 4 | 16.75286 2.525696 6.63 0.000 11.77119 21.73453
1 2 | 2.287037 2.285571 1.00 0.318 -2.221015 6.79509
1 3 | 6.380787 2.128954 3.00 0.003 2.181646 10.57993
1 4 | 6.921652 2.238549 3.09 0.002 2.506347 11.33696
|
_cons | 41.82609 1.698765 24.62 0.000 38.47545 45.17672
------------------------------------------------------------------------------
Again, this model has the same overall F, degrees of freedom and R2 as before. So, it is a different reparameterization of our “full” model. This time the “interaction” coefficients are simple contrasts. To get the three degree of freedom simple effects we need to run the following test commands.
test 0.female#2.grp 0.female#3.grp 0.female#4.grp
( 1) 0b.female#2.grp = 0
( 2) 0b.female#3.grp = 0
( 3) 0b.female#4.grp = 0
F( 3, 192) = 15.33
Prob > F = 0.0000
test 1.female#2.grp 1.female#3.grp 1.female#4.grp
( 1) 1.female#2.grp = 0
( 2) 1.female#3.grp = 0
( 3) 1.female#4.grp = 0
F( 3, 192) = 4.55
Prob > F = 0.0042
You can obtain the same simple effects from the “full” model with this Stata 12 code.
regress write i.grp i.female#i.grp contrast grp@female
Example 1.3
Let’s push things one step further and remove all of the main effects from our model, leaving only the interaction term.
regress write i.female#i.grp
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 11.05
Model | 5135.17494 7 733.59642 Prob > F = 0.0000
Residual | 12743.7001 192 66.3734378 R-squared = 0.2872
-------------+------------------------------ Adj R-squared = 0.2612
Total | 17878.875 199 89.843593 Root MSE = 8.147
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female#grp |
0 2 | 7.31677 2.458951 2.98 0.003 2.466743 12.1668
0 3 | 10.10248 2.292658 4.41 0.000 5.580454 14.62452
0 4 | 16.75286 2.525696 6.63 0.000 11.77119 21.73453
1 1 | 9.136876 2.311726 3.95 0.000 4.577236 13.69652
1 2 | 11.42391 2.377259 4.81 0.000 6.735015 16.11281
1 3 | 15.51766 2.227099 6.97 0.000 11.12494 19.91039
1 4 | 16.05853 2.332086 6.89 0.000 11.45873 20.65833
|
_cons | 41.82609 1.698765 24.62 0.000 38.47545 45.17672
------------------------------------------------------------------------------
Again, the overall F, degrees of freedom and R2 are the same as our “full” model. This model is a variation of a cell means model in which the intercept (41.82609) is the mean for the cell female = 0 and grp = 1. The “interaction” coefficients give the difference between each of the cell means and the mean for cell(0,1).
We can get a clearer picture of the cell means model by rerunning the analysis with the noconstant option and using ibn factor variable notation to suppress a reference group.
regress write ibn.female#ibn.grp, nocons
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 8, 192) = 1058.74
Model | 562175.3 8 70271.9125 Prob > F = 0.0000
Residual | 12743.7001 192 66.3734378 R-squared = 0.9778
-------------+------------------------------ Adj R-squared = 0.9769
Total | 574919 200 2874.595 Root MSE = 8.147
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female#grp |
0 1 | 41.82609 1.698765 24.62 0.000 38.47545 45.17672
0 2 | 49.14286 1.777819 27.64 0.000 45.63629 52.64942
0 3 | 51.92857 1.539636 33.73 0.000 48.8918 54.96534
0 4 | 58.57895 1.869048 31.34 0.000 54.89244 62.26545
1 1 | 50.96296 1.567889 32.50 0.000 47.87046 54.05546
1 2 | 53.25 1.662997 32.02 0.000 49.96991 56.53009
1 3 | 57.34375 1.440198 39.82 0.000 54.50311 60.18439
1 4 | 57.88462 1.597756 36.23 0.000 54.73321 61.03602
------------------------------------------------------------------------------
This model has 8 and 192 degrees of freedom. The overall F and R2 are very different from the previous model although you will note that the sums of squares residual are the same in both models. This time each of the coefficients are the individual cell means. Even though the model seems very different we can replicate the coefficients from the previous model using lincom.
For example, the first coefficient in the previous model is 7.31677 (2.458951) with t = 2.98, i.e., the difference in cell means between cell(0,2) and cell(0,1). Here is the lincom code to obtain that value.
lincom 0.female#2.grp - 0.female#1.grp
( 1) - 0bn.female#1bn.grp + 0bn.female#2.grp = 0
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 7.31677 2.458951 2.98 0.003 2.466743 12.1668
------------------------------------------------------------------------------
Case 2: Categorical by continuous interaction
Consider the following model with a categorical and a continuous predictor.
regress write i.grp##c.socst
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 19.01
Model | 7319.63342 7 1045.66192 Prob > F = 0.0000
Residual | 10559.2416 192 54.9960499 R-squared = 0.4094
-------------+------------------------------ Adj R-squared = 0.3879
Total | 17878.875 199 89.843593 Root MSE = 7.4159
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
grp |
2 | -9.264093 7.699529 -1.20 0.230 -24.45062 5.92243
3 | 8.384216 7.052153 1.19 0.236 -5.525425 22.29386
4 | 5.122424 10.11178 0.51 0.613 -14.82202 25.06687
|
socst | .4307724 .0994109 4.33 0.000 .2346948 .6268501
|
grp#c.socst |
2 | .2259628 .1559057 1.45 0.149 -.0815451 .5334706
3 | -.0850639 .1377873 -0.62 0.538 -.3568351 .1867073
4 | .0064412 .1817305 0.04 0.972 -.3520035 .3648858
|
_cons | 27.36662 4.596719 5.95 0.000 18.30007 36.43318
------------------------------------------------------------------------------
This time the overall F is 19.01 with 7 and 192 degrees of freedom and an R2 of .4094.
Example 2.1
Next, we will rerun the model without socst in the regress command.
regress write i.grp i.grp#c.socst
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 19.01
Model | 7319.63342 7 1045.66192 Prob > F = 0.0000
Residual | 10559.2416 192 54.9960499 R-squared = 0.4094
-------------+------------------------------ Adj R-squared = 0.3879
Total | 17878.875 199 89.843593 Root MSE = 7.4159
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
grp |
2 | -9.264093 7.699529 -1.20 0.230 -24.45062 5.92243
3 | 8.384216 7.052153 1.19 0.236 -5.525425 22.29386
4 | 5.122424 10.11178 0.51 0.613 -14.82202 25.06687
|
grp#c.socst |
1 | .4307724 .0994109 4.33 0.000 .2346948 .6268501
2 | .6567352 .1201002 5.47 0.000 .41985 .8936204
3 | .3457085 .0954087 3.62 0.000 .1575248 .5338923
4 | .4372136 .1521297 2.87 0.005 .1371535 .7372738
|
_cons | 27.36662 4.596719 5.95 0.000 18.30007 36.43318
------------------------------------------------------------------------------
Once again, the overall F, degrees of freedom and R2 are the same as our “full” model. So, once again, this is just a reparameterization of the “full” model.
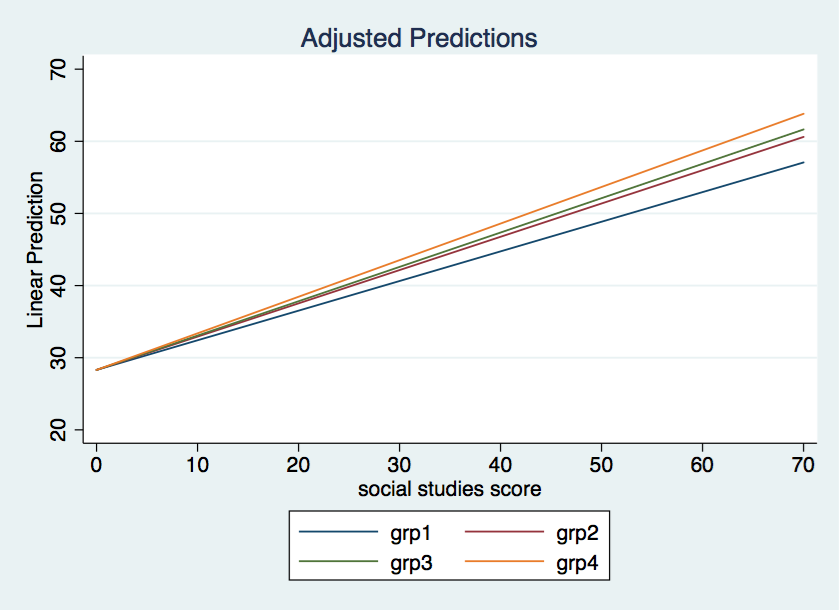
In this model, the “interaction” coefficients represent the simple slopes of write on socst for each of the four levels of grp.
You can obtain the same results with these Stata commands.
regress write i.grp##c.socst margins grp, dydx(socst)
So far, each time we have dropped a term out of the regression command the model has remained the same. Sure, the coefficients are different but the overall F, degrees of freedom and R2 have remained the same. If we drop the categorical variable (grp) from our model we will lose three degrees of freedom and the overall F and R2 will change. Let’s see What happens.
Example 2.2
regress write c.socst i.grp#c.socst
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 4, 195) = 31.73
Model | 7048.83282 4 1762.2082 Prob > F = 0.0000
Residual | 10830.0422 195 55.5386779 R-squared = 0.3943
-------------+------------------------------ Adj R-squared = 0.3818
Total | 17878.875 199 89.843593 Root MSE = 7.4524
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
socst | .4110007 .0650009 6.32 0.000 .2828056 .5391958
|
grp#c.socst |
2 | .0505514 .0318924 1.59 0.115 -.0123469 .1134497
3 | .065381 .0302781 2.16 0.032 .0056664 .1250956
4 | .0963406 .0320259 3.01 0.003 .0331789 .1595023
|
_cons | 28.30563 2.891027 9.79 0.000 22.60393 34.00733
------------------------------------------------------------------------------
This time things are very different. The overall F, degrees of freedom and R2 differ from the “full” model. This model is not a simple reparameterization of of the original model. The coefficients in this model do not have a simple interpretation. This model may, in fact, be misspecified.
So here’s what’s going on in this model. There is just one intercept for the regression lines in each of the four levels of grp. That intercept equals 28.30563. The coefficients for the “interaction” are the differences in slopes between each grp versus grp1. We can show this using the margins command. We will begin by computing the intercepts for each grp.
margins, at(grp=(1 2 3 4) socst=0) noatlegend
Adjusted predictions Number of obs = 200
Model VCE : OLS
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | 28.30563 2.891027 9.79 0.000 22.63932 33.97194
2 | 28.30563 2.891027 9.79 0.000 22.63932 33.97194
3 | 28.30563 2.891027 9.79 0.000 22.63932 33.97194
4 | 28.30563 2.891027 9.79 0.000 22.63932 33.97194
------------------------------------------------------------------------------
Next, we will compute the slopes. We will include the post option so that we can compute the differences in slopes using the lincom command.
margins, dydx(socst) at(grp=(1 2 3 4)) noatlegend post
Average marginal effects Number of obs = 200
Model VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : socst
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
socst |
_at |
1 | .4110007 .0650009 6.32 0.000 .2836012 .5384002
2 | .4615521 .0593735 7.77 0.000 .3451821 .577922
3 | .4763817 .0535655 8.89 0.000 .3713952 .5813681
4 | .5073413 .0519691 9.76 0.000 .4054838 .6091988
------------------------------------------------------------------------------
/* slope 1 vs slope 2 */
lincom 2._at-1._at
( 1) - [socst]1bn._at + [socst]2._at = 0
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .0505514 .0318924 1.59 0.113 -.0119566 .1130594
------------------------------------------------------------------------------
/* slope 1 vs slope 3 */
lincom 3._at-1._at
( 1) - [socst]1bn._at + [socst]3._at = 0
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .065381 .0302781 2.16 0.031 .006037 .124725
------------------------------------------------------------------------------
/* slope 1 cs slope 4 */
lincom 4._at-1._at
( 1) - [socst]1bn._at + [socst]4._at = 0
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .0963406 .0320259 3.01 0.003 .0335709 .1591103
------------------------------------------------------------------------------
The values computed by the lincom commands have the same values as the “interaction” coefficients in the regression model we ran.
A plot of the model looks like this.
You will need to decide from looking at the plot whether this is truly the type of model you are interested in. If the above model is very different from what you expected then you may have run a mispecified model.
Example 2.3
This time we will run an “interaction” only model.
regress write i.grp#c.socst
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 4, 195) = 31.73
Model | 7048.83282 4 1762.2082 Prob > F = 0.0000
Residual | 10830.0422 195 55.5386779 R-squared = 0.3943
-------------+------------------------------ Adj R-squared = 0.3818
Total | 17878.875 199 89.843593 Root MSE = 7.4524
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
grp#c.socst |
1 | .4110007 .0650009 6.32 0.000 .2828056 .5391958
2 | .4615521 .0593735 7.77 0.000 .3444554 .5786487
3 | .4763817 .0535655 8.89 0.000 .3707396 .5820238
4 | .5073413 .0519691 9.76 0.000 .4048477 .6098349
|
_cons | 28.30563 2.891027 9.79 0.000 22.60393 34.00733
------------------------------------------------------------------------------
This example has exactly the same fit (overall F, degrees of freedom and R2) as the previous example where we dropped the grp term. Instead of a three degree of freedom “interaction” Stata give us a four degree of freedom term in which the coefficient are the slopes within each cell.
Case 3: Continuous by continuous interaction
Let’s look at a “full” model using math and socst as predictors of read.
regress read c.math##c.socst
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 78.61
Model | 11424.7622 3 3808.25406 Prob > F = 0.0000
Residual | 9494.65783 196 48.4421318 R-squared = 0.5461
-------------+------------------------------ Adj R-squared = 0.5392
Total | 20919.42 199 105.122714 Root MSE = 6.96
--------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
math | -.1105123 .2916338 -0.38 0.705 -.6856552 .4646307
socst | -.2200442 .2717539 -0.81 0.419 -.7559812 .3158928
|
c.math#c.socst | .0112807 .0052294 2.16 0.032 .0009677 .0215938
|
_cons | 37.84271 14.54521 2.60 0.010 9.157506 66.52792
--------------------------------------------------------------------------------
estimates store m1
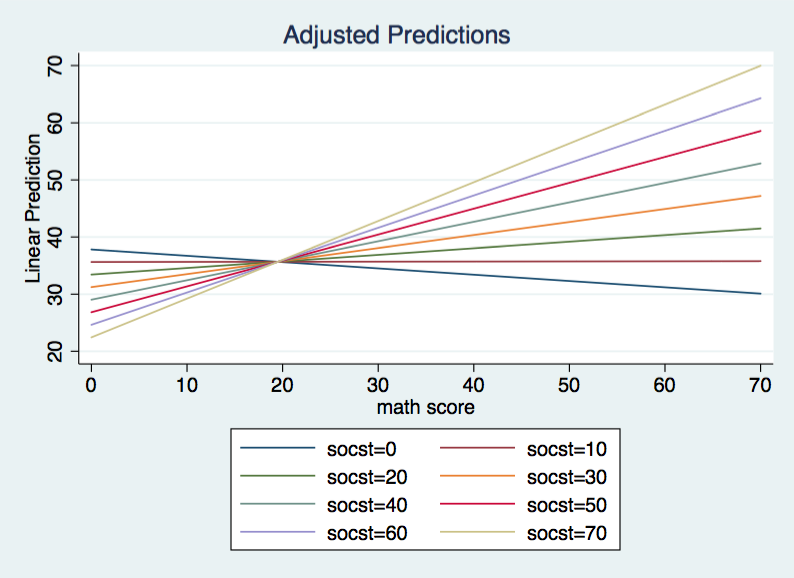
The overall F is 78.61 with 3 and 196 degrees of freedom for the model and an R2 of .5461. The intercept is 37.84271 when both math and socst equal zero. For each unit change in socst the slope of read on math increases by .0112807. Here is what the graph of this model looks when plotted over the range of 0 to 70 for both variables.
One way to think about this model is that there is a regression line for each value of socst. and these regression lines differ in both intercepts and slopes although they all intersect when math equals 19.51.
Example 3.1
Next, we will rerun the regression leaving the main effect for socst out of the model.
regress read c.math c.math#c.socst
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 2, 197) = 117.80
Model | 11393.0014 2 5696.50068 Prob > F = 0.0000
Residual | 9526.41864 197 48.357455 R-squared = 0.5446
-------------+------------------------------ Adj R-squared = 0.5400
Total | 20919.42 199 105.122714 Root MSE = 6.954
--------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
math | .1097745 .1049659 1.05 0.297 -.0972266 .3167757
|
c.math#c.socst | .0071334 .0010534 6.77 0.000 .0050559 .0092108
|
_cons | 26.3823 3.349592 7.88 0.000 19.77664 32.98796
--------------------------------------------------------------------------------
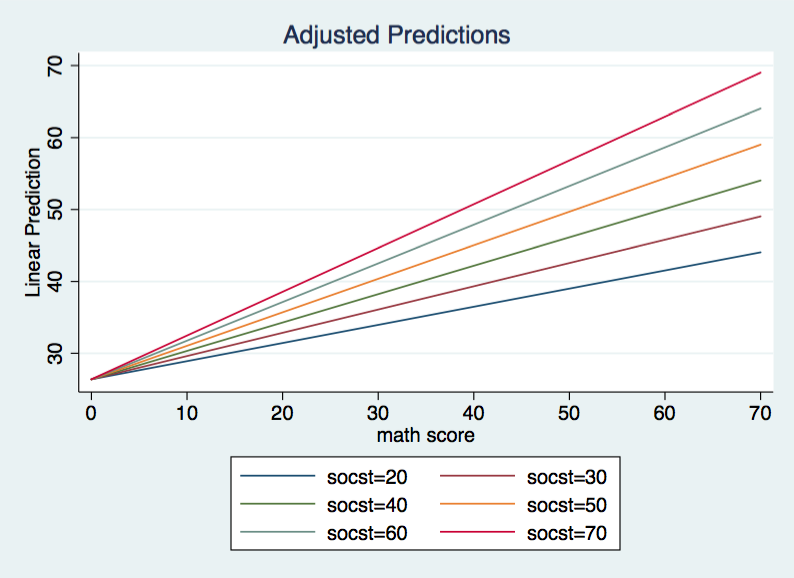
Now the overall F is 117.80 with 2 and 197 degrees of freedom for the model and an R2 of .5446. Let’s jump straight to the graph of this model.
Again, we have a model with different slopes for different values of socst. However, this time each regression line has the same intercept, 26.3823. The researcher needs to decide whether this model makes theoretical sense. If the researcher concludes that the model does make theoretical sense then it is possible to test whether the data can support the model with a common intercept. Basically, we will test to see if the model without socst fits significantly worse than the “full” model. We will do this using the lrtest command.
lrtest m1 . Likelihood-ratio test LR chi2(1) = 0.67 (Assumption: . nested in m1) Prob > chi2 = 0.4138
This test is equivalent to testing the coefficient for socst in the “full” model.
estimates restore m1
test socst
( 1) socst = 0
F( 1, 196) = 0.66
Prob > F = 0.4191
The tests above support the hypothesis that the model without socst does not fit the data significantly worse than the “full” model.
If instead of dropping socst we had dropped math the graph of the model would have looked very similar. The degrees of freedom would be be the same and the overall F and R2 would have been close. Both the intercept and “interaction” coefficient are also different, but not in any noticeable way. The same thing happens when we drop both math and socst. The graph is similar and there are small differences in the overall F and R2. The model with only the “interaction” term has 1 and 198 degrees of freedom.
The most likely reason that these three model appear so similar is that when the “interaction” is in the model neither predictor is significant. Further both math and socst are scaled similarly with nearly equal means and standard deviations.
Concluding remarks
When you drop one or both predictors from a model with an interaction term, one of two things can happen. 1) The model remains the same but the coefficient are reparameterizations of the original estimates. This situation occurs with categorical variables because Stata adds additional degrees of freedom to the “interaction” term so that overall the degrees of freedom and fit of the model do not change. Or, 2) The model changes, such that, it is no longer the same model at all. This occurs with continuous predictors and results in a decrease in the model degrees of freedom as well as a substantial change in the meaning of the coefficients.