This page shows an example of an ordered logistic regression analysis with footnotes explaining the output. The data were collected on 200 high school students and are scores on various tests, including science, math, reading and social studies. The outcome measure in this analysis is socio-economic status (ses)- low, medium and high- from which we are going to see what relationships exist with science test scores (science), social science test scores (socst) and gender (female). Our response variable, ses, is going to be treated as ordinal under the assumption that the levels of ses status have a natural ordering (low to high), but the distances between adjacent levels are unknown. The first half of this page interprets the coefficients in terms of ordered log-odds (logits) and the second half interprets the coefficients in terms of proportional odds.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2, clear
ologit ses science socst female
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -195.01878
Iteration 2: log likelihood = -194.80294
Iteration 3: log likelihood = -194.80235
Ordered logit estimates Number of obs = 200
LR chi2(3) = 31.56
Prob > chi2 = 0.0000
Log likelihood = -194.80235 Pseudo R2 = 0.0749
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
science | .0300201 .0165861 1.81 0.070 -.0024882 .0625283
socst | .0531819 .015271 3.48 0.000 .0232513 .0831126
female | -.4823977 .2796939 -1.72 0.085 -1.030588 .0657922
-------------+----------------------------------------------------------------
_cut1 | 2.754675 .869481 (Ancillary parameters)
_cut2 | 5.10548 .9295388
------------------------------------------------------------------------------
Iteration Loga
Iteration 0: log likelihood = -210.58254 Iteration 1: log likelihood = -195.01878 Iteration 2: log likelihood = -194.80294 Iteration 3: log likelihood = -194.80235
a. This is a listing of the log likelihoods at each iteration. Remember that ordered logistic regression, like binary and multinomial logistic regression, uses maximum likelihood estimation, which is an iterative procedure. The first iteration (called iteration 0) is the log likelihood of the “null” or “empty” model; that is, a model with no predictors. At the next iteration, the predictor(s) are included in the model. At each iteration, the log likelihood increases because the goal is to maximize the log likelihood. When the difference between successive iterations is very small, the model is said to have “converged”, the iterating stops, and the results are displayed. For more information on this process for binary outcomes, see Regression Models for Categorical and Limited Dependent Variables by J. Scott Long (pages 52-61).
Model Summary
Ordered logit estimates Number of obsc = 200
LR chi2(3)d = 31.56
Prob > chi2e = 0.0000
Log likelihood = -194.80235b Pseudo R2f = 0.0749
b. Log Likelihood – This is the log likelihood of the fitted model. It is used in the Likelihood Ratio Chi-Square test of whether all predictors’ regression coefficients in the model are simultaneously zero and in tests of nested models.
c. Number of obs – This is the number of observations used in the ordered logistic regression. It may be less than the number of cases in the dataset if there are missing values for some variables in the equation. By default, Stata does a listwise deletion of incomplete cases.
d. LR chi2(3) – This is the Likelihood Ratio (LR) Chi-Square test that at least one of the predictors’ regression coefficient is not equal to zero in the model. The number in the parenthesis indicates the degrees of freedom of the Chi-Square distribution used to test the LR Chi-Square statistic and is defined by the number of predictors in the model. The LR Chi-Square statistic can be calculated by -2*( L(null model) – L(fitted model)) = -2*((-210.583) – (-194.802)) = 31.560, where L(null model) is from the log likelihood with just the response variable in the model (Iteration 0) and L(fitted model) is the log likelihood from the final iteration (assuming the model converged) with all the parameters.
e. Prob > chi2 – This is the probability of getting a LR test statistic as extreme as, or more so, than the observed under the null hypothesis; the null hypothesis is that all of the regression coefficients in the model are equal to zero. In other words, this is the probability of obtaining this chi-square statistic (31.56) if there is in fact no effect of the predictor variables. This p-value is compared to a specified alpha level, our willingness to accept a type I error, which is typically set at 0.05 or 0.01. The small p-value from the LR test, <0.00001, would lead us to conclude that at least one of the regression coefficients in the model is not equal to zero. The parameter of the Chi-Square distribution used to test the null hypothesis is defined by the degrees of freedom in the prior line, chi2(3).
f. Pseudo R2 – This is McFadden’s pseudo R-squared. Logistic regression does not have an equivalent to the R-squared that is found in OLS regression; however, many people have tried to come up with one. There are a wide variety of pseudo R-squared statistics which can give contradictory conclusions. Because this statistic does not mean what R-squared means in OLS regression (the proportion of variance for the response variable explained by the predictors), we suggest interpreting this statistic with great caution.
Parameter Estimates
------------------------------------------------------------------------------
sesg| Coef.h Std. Err.i zj P>|z|j [95% Conf. Interval]k
-------------+----------------------------------------------------------------
science | .0300201 .0165861 1.81 0.070 -.0024882 .0625283
socst | .0531819 .015271 3.48 0.000 .0232513 .0831126
female | -.4823977 .2796939 -1.72 0.085 -1.030588 .0657922
-------------+----------------------------------------------------------------
_cut1 | 2.754675 .869481 (Ancillary parameters)
_cut2 | 5.10548 .9295388
------------------------------------------------------------------------------
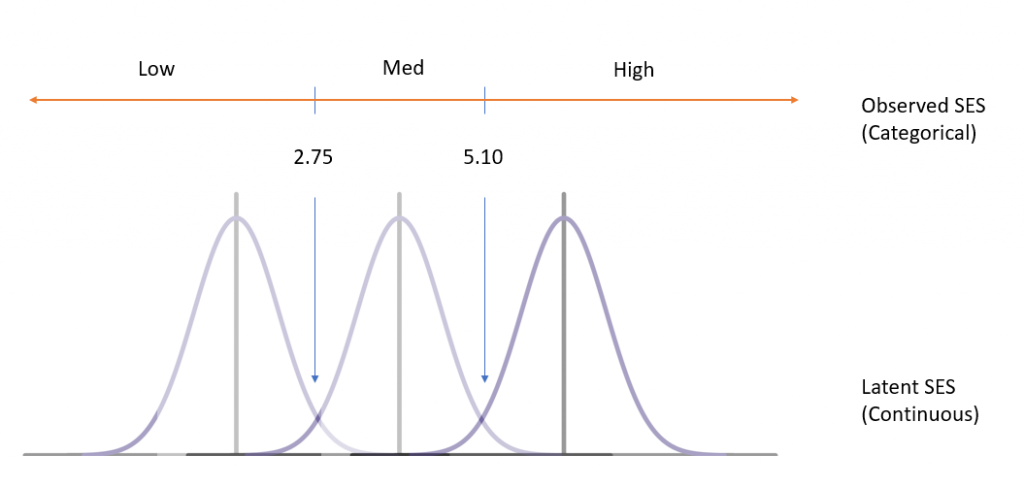
g. ses – This is the response variable in the ordered logistic regression. Underneath ses are the predictors in the models and the cut points for the adjacent levels of the latent response variable. The diagram below represents the observed categorical SES mapped to the latent continuous SES. Those who receive a latent score less than 2.75 are classified as “Low SES”, those who receive a latent score between 2.75 and 5.10 are classified as “Middle SES” and those greater than 5.10 are classified as “High SES”.
h. Coef. – These are the ordered log-odds (logit) regression coefficients. Standard interpretation of the ordered logit coefficient is that for a one unit increase in the predictor, the response variable level is expected to change by its respective regression coefficient in the ordered log-odds scale while the other variables in the model are held constant. Interpretation of the ordered logit estimates is not dependent on the ancillary parameters; the ancillary parameters are used to differentiate the adjacent levels of the response variable. However, since the ordered logit model estimates one equation over all levels of the dependent variable, a concern is whether our one-equation model is valid or a more flexible model is required. We can test this hypothesis with the test for proportional odds test (a.k.a. Brant test of parallel regression assumption). This test can be downloaded by typing search spost9 in the command line and using the brant command (see How can I use the search command to search for programs and get additional help? for more information about using search).
science – This is the ordered log-odds estimate for a one unit increase in science score on the expected ses level given the other variables are held constant in the model. If a subject were to increase his science score by one point, his ordered log-odds of being in a higher ses category would increase by 0.03 while the other variables in the model are held constant.
socst – This is the ordered log-odds estimate for a one unit increase in socst score on the expected ses level given the other variables are held constant in the model. A one unit increase in socst test scores would result in a 0.0532 unit increase in the ordered log-odds of being in a higher ses category while the other variables in the model are held constant.
female – This is the ordered log-odds estimate of comparing females to males on expected ses given the other variables are held constant in the model. The ordered logit for females being in a higher ses category is 0.4824 less than males when the other variables in the model are held constant.
Ancillary parameters – These refer to the cutpoints (a.k.a. thresholds) used to differentiate the adjacent levels of the response variable. A threshold can then be defined to be points on the latent variable, a continuous unobservable mechanism/phenomena, that result in the different observed values on the proxy variable (the levels of our dependent variable used to measure the latent variable).
_cut1 – This is the estimated cutpoint on the latent variable used to differentiate low ses from middle and high ses when values of the predictor variables are evaluated at zero. Subjects that had a value of 2.75 or less on the underlying latent variable that gave rise to our ses variable would be classified as low ses given they were male (the variable female evaluated at zero) and had zero science and socst test scores.
_cut2 – This is the estimated cutpoint on the latent variable used to differentiate low and middle ses from high ses when values of the predictor variables are evaluated at zero. Subjects that had a value of 5.11 or greater on the underlying latent variable that gave rise to our ses variable would be classified as high ses given they were male and had zero science and socst test scores. Subjects that had a value between 2.75 and 5.11 on the underlying latent variable would be classified as middle ses.
i. Std. Err. – These are the standard errors of the individual regression coefficients. They are used in both the calculation of the z test statistic, superscript j, and the confidence interval of the regression coefficient, superscript k.
j. z and P>|z| – These are the test statistics and p-value, respectively, for the null hypothesis that an individual predictor’s regression coefficient is zero given that the rest of the predictors are in the model. The test statistic z is the ratio of the Coef. to the Std. Err. of the respective predictor. The z value follows a standard normal distribution which is used to test against a two-sided alternative hypothesis that the Coef. is not equal to zero. The probability that a particular z test statistic is as extreme as, or more so, than what has been observed under the null hypothesis is defined by P>|z|.
The z test statistic for the predictor science (0.030/0.017) is 1.81 with an associated p-value of 0.070. If we set our alpha level to 0.05, we would fail to reject the null hypothesis and conclude that the regression coefficient for science has not been found to be statistically different from zero in estimating ses given socst and female are in the model.
The z test statistic for the predictor socst (0.053/0.015) is 3.48 with an associated p-value of <0.0001. If we again set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for socst has been found to be statistically different from zero in estimating ses given that science and female are in the model. The interpretation for a dichotomous variable such as female, parallels that of a continuous variable: the observed difference between males and females on ses status was not found to be statistically significant at the 0.05 level when controlling for socst and science (p=0.085).
k. [95% Conf. Interval] – This is the Confidence Interval (CI) for an individual regression coefficient given the other predictors are in the model. For a given predictor with a level of 95% confidence, we’d say that we are 95% confident that the “true” population regression coefficient lies in between the lower and upper limit of the interval. It is calculated as the Coef. ± (zα/2)*(Std.Err.), where zα/2 is a critical value on the standard normal distribution. The CI is equivalent to the z test statistic: if the CI includes zero, we’d fail to reject the null hypothesis that a particular regression coefficient is zero given the other predictors are in the model. An advantage of a CI is that it is illustrative; it provides a range where the “true” parameter may lie.
Odds Ratio Interpretation
The following is the interpretation of the ordered logistic regression in terms of proportional odds ratios and can be obtained by specifying the or option. This part of the interpretation applies to the output below.
ologit ses science socst female, or
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -195.01878
Iteration 2: log likelihood = -194.80294
Iteration 3: log likelihood = -194.80235
Ordered logit estimates Number of obs = 200
LR chi2(3) = 31.56
Prob > chi2 = 0.0000
Log likelihood = -194.80235 Pseudo R2 = 0.0749
------------------------------------------------------------------------------
ses | Odds Ratioa Std. Err. z P>|z| [95% Conf. Interval]b
-------------+----------------------------------------------------------------
science | 1.030475 .0170916 1.81 0.070 .9975149 1.064525
socst | 1.054622 .0161052 3.48 0.000 1.023524 1.086664
female | .6173015 .1726554 -1.72 0.085 .3567972 1.068005
------------------------------------------------------------------------------
a. Odds Ratio – These are the proportional odds ratios for the ordered logit model (a.k.a. proportional odds model) shown earlier. They can be obtained by exponentiating the ordered logit coefficients, ecoef., or by specifying the or option. Recall that ordered logit model estimates a single equation (regression coefficients) over the levels of the dependent variable. Now, if we view the change in levels in a cumulative sense and interpret the coefficients in odds, we are comparing the people who are in groups greater than k versus those who are in groups less than or equal to k, where k is the level of the response variable. The interpretation would be that for a one unit change in the predictor variable, the odds for cases in a group that is greater than k versus less than or equal to k are the proportional odds times larger. For a general discussion of OR, we refer to the following Stata FAQ for binary logistic regression: How do I interpret odds ratios in logistic regression?
science – This is the proportional odds ratio for a one unit increase in science score on ses level given that the other variables in the model are held constant. Thus, for a one unit increase in science test score, the odds of high ses versus the combined middle and low ses categories are 1.03 times greater, given the other variables are held constant in the model. Likewise, for a one unit increase in science test score, the odds of the combined high and middle ses versus low ses are 1.03 times greater, given the other variables are held constant.
socst – This is the proportional odds ratio for a one unit increase in socst score on ses level given that the other variables in the model are held constant. Thus, for a one unit increase in socst test score, the odds of high ses versus the combined middle and low ses are 1.05 times greater, given the other variables are held constant in the model. Likewise, for a one unit increase in socst test score, the odds of the combined high and middle ses versus low ses are 1.05 times greater, given the other variables are held constant.
female – This is the proportional odds ratio of comparing females to males on ses given the other variables in the model are held constant. For females, the odds of high ses versus the combined middle and low ses are 0.6173 times lower than for males, given the other variables are held constant. Likewise, the odds of the combined categories of high and middle ses versus low ses is 0.6173 times lower for females compared to males, given the other variables are held constant in the model.
b. [95% Conf. Interval] – This is the CI for the proportional odds ratio given the other predictors are in the model. For a given predictor with a level of 95% confidence, we’d say that we are 95% confident that the “true” population proportional odds ratio lies between the lower and upper limit of the interval. The CI is equivalent to the z test statistic: if the CI includes one (not zero, because we are working with odds ratios), we’d fail to reject the null hypothesis that a particular regression coefficient is one given the other predictors are in the model. An advantage of a CI is that it is illustrative; it provides a range where the “true” proportional odds ratio may lie.