This page shows an example of zero-inflated negative binomial regression analysis with footnotes explaining the output in Stata. The data collected were academic information on 316 students at two different schools. The response variable is days absent during the school year (daysabs). We explore its relationship with math standardized test scores (mathnce), language standardized test scores (langnce), and gender (female).
As assumed for a negative binomial model, our response variable is a count variable and the variance of the response variable is greater than the mean of the response variable. Sometimes when analyzing a response variable that is a count variable, the number of zeroes may seem excessive. With the example dataset in mind, consider the processes that could lead to a response variable value of zero. A student might be absent zero days during the school year if he never gets sick and never skips school. Another student might be absent zero days during the school year because her parents insist she go to school every day, regardless of illness or desire to skip school. These two students will look identical in the response variable, but they have arrived at the same outcome through two different processes. The first student could have been absent during the school year (had he become ill or opted to skip school), but was not. The second student was certain to be absent zero days. The second student will be referred to from this point forward as a “certain zero”. Thus, the number of zeroes may be inflated and the number of students absent for zero days cannot be explained in the same manner as the number of students that were absent for more than zero days. Some students were absent zero days for the same reasons other students were absent one, two, or three days (health and truancy) and while some students were absent zero days for a different set of reasons.
A standard negative binomial model would not distinguish between these two processes, but a zero-inflated model allows for and accommodates this complication. When analyzing a dataset with an excessive number of outcome zeros and two possible processes that arrive at a zero outcome, a zero-inflated model should be considered. We can look at summary statistics to try to gauge if the data are over-dispersed and a histogram of the response variable to see if the number of zeros is excessive. (If two processes generated the zeroes in the response variable, but there is not an excessive number of zeroes, a zero-inflated model may or may not be used.)
use https://stats.idre.ucla.edu/stat/stata/notes/lahigh, clear
generate female = (gender == 1)
summarize daysabs
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
daysabs | 316 5.810127 7.449003 0 45
From here, we can see that the variance of our outcome (the standard deviation squared) is larger than the mean.
histogram daysabs, discrete freq
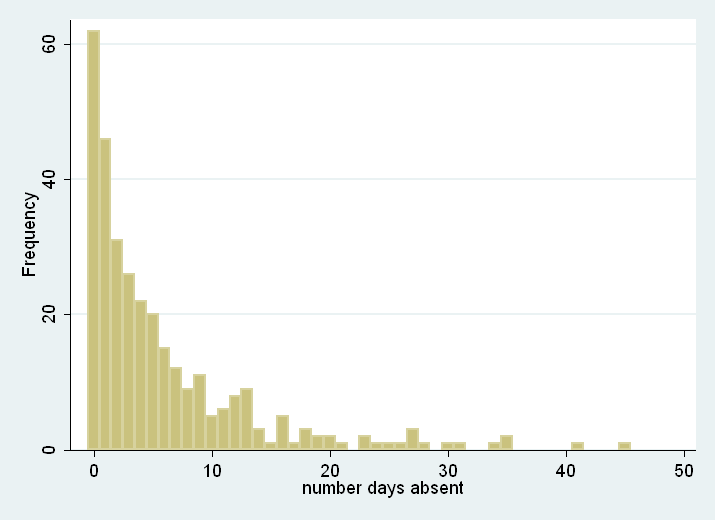
While zero is the most common number of days absent, it is difficult to see from this histogram if the number of zeroes is in excess of what we would expect from a negative binomial model. Thus, we can run a zero-inflated negative binomial model and test whether it better predicts our response variable than a standard negative binomial model.
The zero-inflated negative binomial regression generates two separate models and then combines them. First, a logit model is generated for the “certain zero” cases described above, predicting whether or not a student would be in this group. Then, a negative binomial model is generated predicting the counts for those students who are not certain zeros. Finally, the two models are combined. When running zero-inflated negative binomial in Stata, you must specify both models: first the count model, then the model predicting the certain zeros. In this example, we are predicting count with mathnce, langnce and female, and predicting the certain zeros with mathnce and langnce.
zinb daysabs mathnce langnce female, inflate(mathnce langnce)
Fitting constant-only model:
Iteration 0: log likelihood = -989.38831
Iteration 1: log likelihood = -898.75216
Iteration 2: log likelihood = -890.9426
Iteration 3: log likelihood = -890.11078
Iteration 4: log likelihood = -890.0709
Iteration 5: log likelihood = -890.07088
Fitting full model:
Iteration 0: log likelihood = -890.07088
Iteration 1: log likelihood = -881.59732
Iteration 2: log likelihood = -880.80421
Iteration 3: log likelihood = -880.77785
Iteration 4: log likelihood = -880.77656
Iteration 5: log likelihood = -880.77656
Zero-inflated negative binomial regression Number of obs = 316
Inflation model: logit Nonzero obs = 254
Zero obs = 62
LR chi2(3) = 18.59
Log likelihood = -880.7766 Prob > chi2 = 0.0003
------------------------------------------------------------------------------
daysabs | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
daysabs |
mathnce | -.0011483 .0050248 -0.23 0.819 -.0109967 .0087001
langnce | -.014174 .0058023 -2.44 0.015 -.0255463 -.0028018
female | .423556 .1403317 3.02 0.003 .1485109 .698601
_cons | 2.274443 .2113109 10.76 0.000 1.860281 2.688604
-------------+----------------------------------------------------------------
inflate |
mathnce | .0371789 .0598117 0.62 0.534 -.0800499 .1544076
langnce | .0078224 .0900147 0.09 0.931 -.1686031 .1842479
_cons | -6.588474 4.472095 -1.47 0.141 -15.35362 2.176671
-------------+----------------------------------------------------------------
/lnalpha | .2132175 .1359407 1.57 0.117 -.0532214 .4796564
-------------+----------------------------------------------------------------
alpha | 1.237654 .1682475 .94817 1.615519
------------------------------------------------------------------------------
Iteration History
Fitting constant-only model:a Iteration 0: log likelihood = -989.38831 Iteration 1: log likelihood = -898.75216 Iteration 2: log likelihood = -890.9426 Iteration 3: log likelihood = -890.11078 Iteration 4: log likelihood = -890.0709 Iteration 5: log likelihood = -890.07088 Fitting full model:b Iteration 0: log likelihood = -890.07088 Iteration 1: log likelihood = -881.59732 Iteration 2: log likelihood = -880.80421 Iteration 3: log likelihood = -880.77785 Iteration 4: log likelihood = -880.77656 Iteration 5: log likelihood = -880.77656
a. Fitting constant-only model – This is a listing of the log likelihoods at each iteration for the logistic model predicting whether or not a student is a certain zero. Remember that logistic regression uses maximum likelihood estimation, which is an iterative procedure. The first iteration (called Iteration 0) is the log likelihood of the “null” or “empty” model; that is, a model with intercept only model for the count model and intercept set to zero for inflated model or logistic model. At the next iteration (called Iteration 1), the variables specified for predicting certain zeroes are included in the model. In this example, the predictors for the constant-only model are mathnce and langnce. At each iteration, the log likelihood increases because the goal is to maximize the log likelihood. When the difference between successive iterations is very small, the model is said to have “converged” and the iterating stops. For more information on this process for binary outcomes, see Regression Models for Categorical and Limited Dependent Variables by J. Scott Long (page 52-61).
b. Fitting full model – This is a listing of the log likelihoods at each iteration for the full model, combining the constant-only model with the count model. Again, the fitting of this model is an iterative procedure. Note that the log likelihood of Iteration 0 for the full model is equal to the log likelihood at which the constant-only model had converged. This illustrates that the full model begins with the fitted constant-only model stopped and improves on it with the count model.
Model Summary
Zero-inflated negative binomial regression Number of obse = 316 Nonzero obsf = 254 Zero obsg = 62 Inflation modelc = logit LR chi2(3)h = 18.59 Log likelihoodd = -880.7766 Prob > chi2i = 0.0003
c. Inflation model – This indicates that the inflated model is a logit model, predicting a latent binary outcome: whether or not a student is a certain zero. This also informs the interpretation of the parameter estimates.
d. Log Likelihood – This is the log likelihood of the fitted full model. It is used in the Likelihood Ratio Chi-Square test of whether all predictors’ regression coefficients in the count model are simultaneously zero.
e. Number of obs – This is the number of observations in the dataset for which all of the response and predictor variables are non-missing.
f. Nonzero obs – This is the number of observations in the dataset for which the response variable is not equal to zero.
g. Zero obs – This is the number of observations in the dataset for which the response variable is equal to zero.
h. LR chi2(3) – This is the Likelihood Ratio (LR) Chi-Square test that at least one of the predictors’ regression coefficient in the count model is not equal to zero. The number in the parentheses indicates the degrees of freedom of the Chi-Square distribution used to test the LR Chi-Square statistic and is defined by the number of predictors in the model (3). The LR Chi-Square statistic can be calculated by -2*( L(null model of full model) – L(fitted model of full model)) = -2*((-890.07088) – (-880.77656)) = 18.59.
i. Prob > chi2 – This is the probability of getting a LR test statistic as extreme as, or more so, than the observed statistic under the null hypothesis; the null hypothesis is that is that all of the regression coefficients for count model are simultaneously equal to zero. In other words, this is the probability of obtaining this chi-square statistic (18.59) or one more extreme if there is in fact no effect of the predictor variables in the count model. This p-value is compared to a specified alpha level, our willingness to accept a type I error, which is typically set at 0.05 or 0.01. The small p-value from the LR test, 0.0003, would lead us to conclude that at least one of the regression coefficients in the model is not equal to zero. The parameter of the chi-square distribution used to test the null hypothesis is defined by the degrees of freedom in the prior line, chi2(3).
Parameter Estimates
------------------------------------------------------------------------------ | Coef.l Std. Err.m zn P>|z|o [95% Conf. Interval]p -------------+---------------------------------------------------------------- daysabsj | mathnce | -.0011483 .0050248 -0.23 0.819 -.0109967 .0087001 langnce | -.014174 .0058023 -2.44 0.015 -.0255463 -.0028018 female | .423556 .1403317 3.02 0.003 .1485109 .698601 _cons | 2.274443 .2113109 10.76 0.000 1.860281 2.688604 -------------+---------------------------------------------------------------- inflatek | mathnce | .0371789 .0598117 0.62 0.534 -.0800499 .1544076 langnce | .0078224 .0900147 0.09 0.931 -.1686031 .1842479 _cons | -6.588474 4.472095 -1.47 0.141 -15.35362 2.176671 -------------+---------------------------------------------------------------- /lnalphaq| .2132175 .1359407 1.57 0.117 -.0532214 .4796564 -------------+---------------------------------------------------------------- alphar| 1.237654 .1682475 .94817 1.615519 ------------------------------------------------------------------------------
j. daysabs – This is the response variable predicted by the full model.
k. inflate – This portion of the output refers to the logistic model predicting whether or not a student is a certain zero.
l. Coef. – These are the regression coefficients. The coefficients in the daysabs section of the output are interpreted as you would interpret coefficients from a standard negative binomial model: the expected number of days absent changes by exp(Coef.) for each unit increase in the corresponding predictor.
Predicting Days Absent for Students Not in the “Certain Zero” Group
mathnce – If a subject were to increase his mathnce score by one point, the expected number of days absent in a year would decrease by a factor of exp(-.0011483) = 0.99885236 while holding all other variables in the model constant. Thus, the higher a student’s mathnce score, the fewer predicted days absent.
langnce – If a subject were to increase his langnce score by one point, the expected number of days absent in a year would decrease by a factor of exp(-.014174) = 0.98592598 while holding all other variables in the model constant. Thus, the higher a student’s langnce score, the fewer predicted days absent.
female – The expected number of days absent in a year for a female student is exp(0.423556) = 1.5273833 times the expected number of days in a year for a male student while holding all other variables in the model constant. If a female student and male student are not certain zeros and have identical mathnce and langnce scores, the expected number of days absent for the female student would be 1.5273833 times the expected number of days absent for the male student.
_cons – If all of the predictor variables in the model are evaluated at zero, the predicted number of days absent would be calculated as exp(_cons) = exp(2.274443). For males (the variable female evaluated at zero) with zero mathnce and langnce scores, the predicted number of days absent would be 9.7225021. This may seem very high, considering the mean number of days absent is less than 6, but note that evaluating mathnce and langnce at zero is out of the range of plausible scores.
Predicting Membership in the “Certain Zero” Group
mathnce – If a subject were to increase his mathnce score by one point, the odds that he would be in the “Certain Zero” group would increase by a factor of exp(0.0371789) = 1.0378787. In other words, the higher a student’s mathnce score, the more likely the student is a certain zero.
langnce – If a subject were to increase his langnce score by one point, the odds that he would be in the “Certain Zero” group would increase by a factor of exp(0.0078224) = 1.0078531. In other words, the higher a student’s langnce score, the more likely the student is a certain zero.
_cons – If all of the predictor variables in the model are evaluated at zero, the odds of being in the “Certain Zero” group is exp(-6.588474) = .00137614. This means that the predicted odds of a student with mathnce and langnce scores of zero being a certain zero are .00137614 (though remember that evaluating mathnce and langnce at zero is out of the range of plausible scores).
m. Std. Err. – These are the standard errors of the individual regression coefficients for the two models. They are used in both the calculation of the z test statistic, superscript n, and the confidence interval of the regression coefficient, superscript p.
n. z – This is the test statistic z is the ratio of the Coef. to the Std. Err. of the respective predictor. The z value follows a standard normal distribution which is used to test against a two-sided alternative hypothesis that the Coef. is not equal to zero.
o. P>|z| – This is the probability the z test statistic (or a more extreme test statistic) would be observed under the null hypothesis that a particular predictor’s regression coefficient is zero, given that the rest of the predictors are in the model. For a given alpha level, P>|z| determine whether or not the null hypothesis can be rejected. If P>|z| is less than alpha, then the null hypothesis can be rejected and the parameter estimate is considered significant at that alpha level.
Predicting Days Absent for Students Not in the “Certain Zero” Group
mathnce – The z test statistic for the predictor mathnce is (-0.0011483/0.0050248) = -0.23 with an associated p-value of 0.819. If we set our alpha level to 0.05, we would fail to reject the null hypothesis and conclude that the regression coefficient for mathnce has not been found to be statistically different from zero given langnce and female are in the model.
langnce –The z test statistic for the predictor langnce is (-0.014174/0.0058023) = -2.44 with an associated p-value of 0.015. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for langnce has been found to be statistically different from zero given mathnce and female are in the model.
female – The z test statistic for the predictor female is (0.423556/0.1403317) = 3.02 with an associated p-value of 0.003. If we again set our alpha level to 0.05, we would reject the null hypothesis and conclude that the difference between males and females has been found to be statistically different given that mathnce and langnce are in the model.
_cons – The z test statistic for the intercept, _cons, is (2.274443/0.2113109) = 10.76 with an associated p-value of < 0.001. If we set our alpha level at 0.05, we would reject the null hypothesis and conclude that _cons has been found to be statistically different from zero given mathnce, langnce and female are in the model and evaluated at zero.
Predicting Membership in the “Certain Zero” Group
mathnce – The z test statistic for the predictor mathnce is (0.0371789/0.0598117) = 0.62 with an associated p-value of 0.534. If we again set our alpha level to 0.05, we would fail to reject the null hypothesis and conclude that the regression coefficient for mathnce has not been found to be statistically different from zero given langnce is in the model.
langnce – The z test statistic for the predictor langnce is (0.0078224/0.0900147) = 0.09 with an associated p-value of 0.931. If we set our alpha level to 0.05, we would fail to reject the null hypothesis and conclude that the regression coefficient for langnce has not been found to be statistically different from zero given mathnce is in the model.
_cons -The z test statistic for the intercept, _cons, is (-6.588474/4.472095) = -1.47 with an associated p-value of 0.141. With an alpha level of 0.05, we would fail to reject the null hypothesis and conclude that _cons has not been found to be statistically different from zero given mathnce and langnce are in the model and evaluated at zero.
p. [95% Conf. Interval] – This is the Confidence Interval (CI) for an individual coefficient given that the other predictors are in the model. For a given predictor with a level of 95% confidence, we’d say that we are 95% confident that the “true” coefficient lies between the lower and upper limit of the interval. It is calculated as the Coef. (zα/2)*(Std.Err.), where zα/2 is a critical value on the standard normal distribution. The CI is equivalent to the z test statistic: if the CI includes zero, we’d fail to reject the null hypothesis that a particular regression coefficient is zero given the other predictors are in the model. An advantage of a CI is that it is illustrative; it provides a range where the “true” parameter may lie.
q. /lnalpha – This is the natural log of alpha (the dispersion parameter). If the dispersion parameter is zero, log(dispersion parameter) = -infinity. If this is true, then a Poisson model would be appropriate. We can see the 95% confidence interval for /lnalpha that the value is not -infinity. This is confirmed by the 95% confidence interval about the estimate of alpha that does not contain zero.
r. alpha – This is the dispersion parameter of the count model.
For more information
In cases where there is a question as to which count model to use, the countfit command is helpful for comparing the range of count models. You can download countfit from within Stata by typing search countfit (see How can I used the search command to search for programs and get additional help? for more information about using search).
In times past, the Vuong test had been used to test whether a zero-inflated negative binomial model or a negative binomial model (without the zero-inflation) was a better fit for the data. However, this test is no longer considered valid. Please see The Misuse of The Vuong Test For Non-Nested Models to Test for Zero-Inflation by Paul Wilson for further information.
