This page shows an example of zero-truncated negative binomial regression analysis with footnotes
explaining the output in Stata. The dataset used for this example relates to
hospital stays and contains 1,493 observations. The variable stay gives
the length
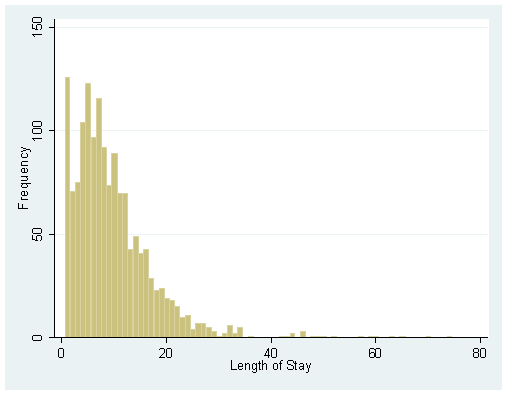
We may be interested in predicting the length of a stay. Stays are measured in days, so we can consider stay as a count variable. However, each stay in the dataset is at least one day–a record would not appear in the dataset if a patient had not gone to the hospital (considered a one-day stay). It would be impossible to have a stay of zero days and be included in the dataset. Thus, stay is zero-truncated. A zero-truncated model allows us to predict stay with this constraint. A negative binomial is appropriate when we are modeling an over-dispersed count variable: that is, a count variable with a variance that is greater than its mean. As we can see from the summary below, the standard deviation of stay is 8.132908. Thus, the variance of stay is (8.132908)2=66.144193, which is significantly larger than the mean of stay, 9.728734.
use https://stats.idre.ucla.edu/stat/stata/dae/ztp, clear
summarize
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
stay | 1493 9.728734 8.132908 1 74
age | 1493 5.233758 1.669273 1 9
hmo | 1493 .1600804 .3668034 0 1
died | 1493 .3429337 .4748486 0 1
histogram stay, discrete freq
Here, we will run a zero-truncated negative binomial model predicting length of stay with patients’ age category, whether or not they are HMO insured, and whether or not they died during the hospital visit. To do this in Stata, we first list our response variable (stay), followed by our predictors (age, hmo and died).
ztnb stay age hmo died
Fitting Zero-truncated poisson model:
Iteration 0: log likelihood = -6908.7992
Iteration 1: log likelihood = -6908.7991
Fitting constant-only model:
Iteration 0: log likelihood = -4817.852
Iteration 1: log likelihood = -4778.7604
Iteration 2: log likelihood = -4770.8734
Iteration 3: log likelihood = -4770.848
Iteration 4: log likelihood = -4770.848
Fitting full model:
Iteration 0: log likelihood = -4755.5912
Iteration 1: log likelihood = -4755.2798
Iteration 2: log likelihood = -4755.2796
Zero-truncated negative binomial regression Number of obs = 1493
LR chi2(3) = 31.14
Dispersion = mean Prob > chi2 = 0.0000
Log likelihood = -4755.2796 Pseudo R2 = 0.0033
------------------------------------------------------------------------------
stay | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | -.0156929 .013107 -1.20 0.231 -.0413822 .0099964
hmo | -.1470576 .0592161 -2.48 0.013 -.263119 -.0309962
died | -.2177714 .0461605 -4.72 0.000 -.3082442 -.1272985
_cons | 2.408328 .071982 33.46 0.000 2.267245 2.54941
-------------+----------------------------------------------------------------
/lnalpha | -.5686389 .0551506 -.6767321 -.4605457
-------------+----------------------------------------------------------------
alpha | .5662957 .0312316 .5082753 .6309393
------------------------------------------------------------------------------
Likelihood-ratio test of alpha=0: chibar2(01) = 4307.04 Prob>=chibar2 = 0.000
Iteration Historya
Fitting Zero-truncated poisson model: Iteration 0: log likelihood = -6908.7992 Iteration 1: log likelihood = -6908.7991 Fitting constant-only model: Iteration 0: log likelihood = -4817.852 Iteration 1: log likelihood = -4778.7604 Iteration 2: log likelihood = -4770.8734 Iteration 3: log likelihood = -4770.848 Iteration 4: log likelihood = -4770.848 Fitting full model: Iteration 0: log likelihood = -4755.5912 Iteration 1: log likelihood = -4755.2798 Iteration 2: log likelihood = -4755.2796
a. Iteration History – This is a listing of the log likelihoods at each iteration. Remember that negative binomial regression uses maximum likelihood estimation, which is an iterative procedure. The first iteration (called Iteration 0) is the log likelihood of the "null" or "empty" model; that is, a model with no predictors. At the next iteration (called Iteration 1), the specified predictors are included in the model. In this example, the predictors are age, hmo and died. At each iteration, the log likelihood increases because the goal is to maximize the log likelihood. When the difference between successive iterations is very small, the model is said to have "converged" and the iterating stops. For more information on this process for binary outcomes, see Regression Models for Categorical and Limited Dependent Variables by J. Scott Long (page 52-61).
Model Summary
Zero-truncated negative binomial regression Number of obsd = 1493
LR chi2(3)e = 31.14
Dispersionb = mean Prob > chi2f = 0.0000
Log likelihoodc = -4755.2796 Pseudo R2g = 0.0033
b. Dispersion – This refers to the method used in modeling the over-dispersion. The default method is mean dispersion.
c. Log likelihood – This is the log likelihood of the fitted model. It is used in the Likelihood Ratio Chi-Square test of whether all predictors’ regression coefficients in the model are simultaneously zero.
d. Number of obs – This is the number of observations in the dataset for which all of the response and predictor variables are non-missing.
e. LR chi2(3) – This is the Likelihood Ratio (LR) Chi-Square test that at least one of the predictors’ regression coefficient is not equal to zero. The number in the parentheses indicates the degrees of freedom of the Chi-Square distribution used to test the LR Chi-Square statistic and is defined by the number of predictors in the model (3).
f. Prob > chi2 – This is the probability of getting a LR test statistic as extreme as, or more so, than the observed statistic under the null hypothesis; the null hypothesis is that all of the regression coefficients across both models are simultaneously equal to zero. In other words, this is the probability of obtaining this chi-square statistic (31.14) or one more extreme if there is in fact no effect of the predictor variables. This p-value is compared to a specified alpha level, our willingness to accept a type I error, which is typically set at 0.05 or 0.01. The small p-value from the LR test, <0.0001, would lead us to conclude that at least one of the regression coefficients in the model is not equal to zero. The parameter of the chi-square distribution used to test the null hypothesis is defined by the degrees of freedom in the prior line, chi2(3).
g. Pseudo R2 – This is McFadden’s pseudo R-squared. Negative binomial regression does not have an equivalent to the R-squared that is found in OLS regression; however, many people have tried to come up with one. There are a wide variety of pseudo-R-square statistics. Because this statistic does not mean what R-square means in OLS regression (the proportion of variance of the response variable explained by the predictors), we suggest interpreting this statistic with great caution. For more information on pseudo R-squareds, see What are Pseudo R-Squareds?.
Parameter Estimates
------------------------------------------------------------------------------
stayh| Coef.i Std. Err.j zk P>|z|l [95% Conf. Interval]m
-------------+----------------------------------------------------------------
age | -.0156929 .013107 -1.20 0.231 -.0413822 .0099964
hmo | -.1470576 .0592161 -2.48 0.013 -.263119 -.0309962
died | -.2177714 .0461605 -4.72 0.000 -.3082442 -.1272985
_cons | 2.408328 .071982 33.46 0.000 2.267245 2.54941
-------------+----------------------------------------------------------------
/lnalphan| -.5686389 .0551506 -.6767321 -.4605457
-------------+----------------------------------------------------------------
alphao| .5662957 .0312316 .5082753 .6309393
------------------------------------------------------------------------------
Likelihood-ratio test of alpha=0:p chibar2(01) = 4307.04 Prob>=chibar2 = 0.000
h. stay – This is the response variable used in the model. Because it is a count variable that cannot be zero, we are using a zero-truncated negative binomial model.
i. Coef. – These are the regression coefficients. These coefficients are interpreted as you would interpret coefficients from a standard negative binomial model: the expected number of days absent changes by exp(Coef.) for each unit increase in the corresponding predictor.
age – A one-unit increase in age group results in the expected length of the stay to decrease by a factor of exp(-0.0156929) = 0.98442959 while holding all other variables in the model constant. Thus, if two patients have the same values for hmo and died (for example, both died while in the hospital and both were insured by HMOs) and one fell into age group 4 and the other into age group 5, the patient in age group 5 would have a predicted hospital stay of 0.98442959 times that of the patient in age group 4. This means age decreases the length of stay when controlling for hmo and died.
hmo – A patient insured by an HMO (hmo = 1) has an expected length of the stay equal to exp(-0.1470576) = 0.86324425 that of a patient not insured by an HMO (hmo = 0) while holding all other variables in the model constant. Thus, if two patients have the same values for age and died (for example, both died while in the hospital and both were in age group 8) and one was insured by an HMO and one was not, the patient insured by an HMO would have a predicted hospital stay of 0.86324425 times that of the patient not insured by an HMO. This means hmo decreases the length of stay when controlling for age and died.
died – A patient who died while in the hospital (died = 1) has an expected length of the stay equal to exp(-.2177714) = 0.80430929 that of a patient who did not die while in the hospital (died = 0) while holding all other variables in the model constant. Thus, if two patients have the same values for age and hmo (for example, both were in age group 8 and both were insured by an HMO) and one died while in the hospital and one did not, then the patient who died would have a predicted hospital stay of 0.80430929 times that of the patient who did not die. This means died decreases the length of stay when controlling for age and hmo.
_cons – If all of the predictor variables in the model are evaluated at zero, the predicted length of the hospital stay would be calculated as exp(_cons) = exp(2.408328) = 11.115361 days. This is the predicted length of a hospital stay for a patient who did not die in the hospital, is not insured by an HMO, and has an age value of zero. However, note that this value is outside of the possible age range.
j. Std. Err. – These are the standard errors of the individual regression coefficients. They are used in both the calculation of the z test statistic, superscript k, and the confidence interval of the regression coefficient, superscript m.
k. z – The test statistic z is the ratio of the Coef. to the Std. Err. of the respective predictor. The z value follows a standard normal distribution which is used to test against a two-sided alternative hypothesis that the Coef. is not equal to zero.
l. P>|z| – This is the probability the z test statistic (or a more extreme test statistic) would be observed under the null hypothesis that a particular predictor’s regression coefficient is zero, given that the rest of the predictors are in the model. For a given alpha level, P>|z| determines whether or not the null hypothesis can be rejected. If P>|z| is less than alpha, then the null hypothesis can be rejected and the parameter estimate is considered statistically significant at that alpha level.
age – The z test statistic for the predictor age is (-0.0156929/0.013107) = -1.20 with an associated p-value of 0.231. If we set our alpha level to 0.05, we would fail to reject the null hypothesis and conclude that the regression coefficient for age has not been found to be statistically different from zero given hmo and died are in the model.
hmo – The z test statistic for the predictor hmo is (-0.1470576/0.0592161) = -2.48 with an associated p-value of 0.013. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for hmo has been found to be statistically different from zero given age and died are in the model.
died – The z test statistic for the predictor died is (-0.2177714/0.0461605) = -4.72 with an associated p-value of <0.001. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for died has been found to be statistically different from zero given hmo and age are in the model.
_cons – The z test statistic for the intercept, _cons, is (2.408328/0.071982) = 33.46 with an associated p-value of < 0.001. If we set our alpha level at 0.05, we would reject the null hypothesis and conclude that _cons has been found to be statistically different from zero given age, hmo and died are in the model and evaluated at zero.
m. [95% Conf. Interval] – This is the Confidence Interval (CI) for an individual coefficient given that the other predictors are in the model. For a given predictor with a level of 95% confidence, we’d say that we are 95% confident that the "true" coefficient lies between the lower and upper limit of the interval. It is calculated as the Coef. (zα/2)*(Std.Err.), where zα/2 is a critical value on the standard normal distribution. The CI is equivalent to the z test statistic: if the CI includes zero, we’d fail to reject the null hypothesis that a particular regression coefficient is zero given the other predictors are in the model. An advantage of a CI is that it is illustrative; it provides a range where the "true" parameter may lie.
n. /lnalpha – This is the natural log of alpha (the dispersion parameter). If the log of the dispersion parameter is zero, then a Poisson model would be appropriate.
o. alpha – This is the dispersion parameter of the count model.
p. Likelihood-ratio test of alpha = 0 – This is the likelihood-ratio chi-square test that the dispersion parameter alpha is equal to zero. The test statistic is negative two times the difference of the log-likelihood from the poisson model and the negative binomial model, -2[-6908.7992 -(-4755.2796)] = 4307.04 with an associated p-value of <0.0001. The large test statistic would suggest that the response variable is over-dispersed and is not sufficiently described by the simpler poisson distribution.