Data: wide versus long
Repeated measures data comes in two different formats: 1) wide or 2) long. In the wide format each subject appears once with the repeated measures in the same observation. For data in the long format there is one observation for each time period for each subject. Here is an example of data in the wide format for four time periods.
id y1 y2 y3 y4 1 3.5 4.5 7.5 7.5 2 6.5 5.5 8.5 8.5
In the above y1 is the response variable at time one. In long form the data look like this.
id time y 1 1 3.5 1 2 4.5 1 3 7.5 1 4 7.5 2 1 6.5 2 2 5.5 2 3 8.5 2 4 8.5
Note that time is an explicit variable with long form data. This format is called person-period data by some researchers.
Stata analyzes repeated measures for both anova and for linear mixed models in long form. On the other hand, SAS and SPSS usually analyze repeated measure anova in wide form. However, both SAS and SPSS require the use long data mixed models.
The example dataset
Our example dataset is cleverly called repeated_measures and can be downloaded with the following command.
use https://stats.idre.ucla.edu/stat/data/repeated_measures, clear
There are a total of eight subjects measured at four time points each. These data are in wide format where y1 is the response at time 1, y2 is the response at time 2, and so on. The subjects are divided into two groups of four subjects using the the variable trt. Here are the basic descriptive statistics at each of the four time points combined and broken out by treatment group.
summarize y1-y4
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
y1 | 8 3 1.690309 1 6.5
y2 | 8 3.75 1.101946 2 5.5
y3 | 8 6.5 1.253566 5 8.5
y4 | 8 9.25 1.101946 7.5 11
tabstat y1-y4, by(trt) stat(n mean sd var)
Summary statistics: N, mean, sd, variance
by categories of: trt
trt | y1 y2 y3 y4
---------+----------------------------------------
1 | 4 4 4 4
| 4.25 4.5 7.5 8.5
| 1.5 .8164966 .8164966 .8164966
| 2.25 .6666667 .6666667 .6666667
---------+----------------------------------------
2 | 4 4 4 4
| 1.75 3 5.5 10
| .5 .8164966 .5773503 .8164966
| .25 .6666667 .3333333 .6666667
---------+----------------------------------------
Total | 8 8 8 8
| 3 3.75 6.5 9.25
| 1.690309 1.101946 1.253566 1.101946
| 2.857143 1.214286 1.571429 1.214286
--------------------------------------------------
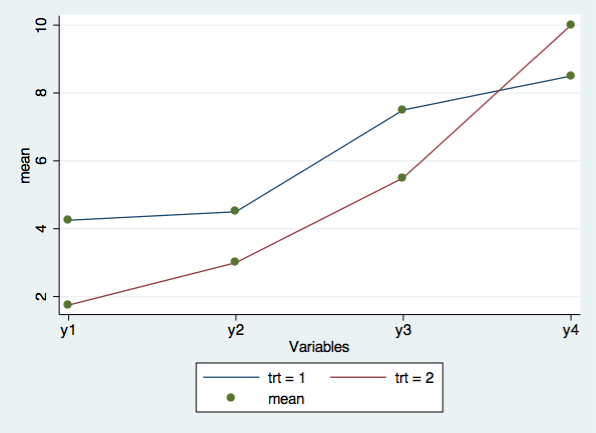
Next, we will graph the eight cell means with the user written command, profileplot. You can download this command by typing search profileplot is the Stata command window.
profileplot y1-y4, by(trt)
Now, let’s look at the correlation and covariance matrices of the responses over time.
correlate y1-y4
(obs=8)
| y1 y2 y3 y4
-------------+------------------------------------
y1 | 1.0000
y2 | 0.8820 1.0000
y3 | 0.9102 0.8273 1.0000
y4 | -0.5752 -0.6471 -0.5171 1.0000
correlate y1-y4, cov
(obs=8)
| y1 y2 y3 y4
-------------+------------------------------------
y1 | 2.85714
y2 | 1.64286 1.21429
y3 | 1.92857 1.14286 1.57143
y4 | -1.07143 -.785714 -.714286 1.21429
Repeated measure anova assumes the within-subject covariance structure is compound symmetric. The covariance matrix above does not appear to have compound symmetry. We will discuss within-subject covariance in greater detail later in the presentation.
Reshape from wide to long
Now that we have looked at some of the descriptive statistics we can reshape the data into long form using the reshape command. The i() option gives the variable that identifies the subject while the j() option creates a new variable that indicates the time period.
reshape long y, i(id) j(time)
(note: j = 1 2 3 4)
Data wide -> long
-----------------------------------------------------------------------------
Number of obs. 8 -> 32
Number of variables 6 -> 4
j variable (4 values) -> time
xij variables:
y1 y2 ... y4 -> y
-----------------------------------------------------------------------------
list, sep(4)
+-----------------------+
| id time trt y |
|-----------------------|
1. | 1 1 1 3.5 |
2. | 1 2 1 4.5 |
3. | 1 3 1 7.5 |
4. | 1 4 1 7.5 |
|-----------------------|
5. | 2 1 1 6.5 |
6. | 2 2 1 5.5 |
7. | 2 3 1 8.5 |
8. | 2 4 1 8.5 |
|-----------------------|
9. | 3 1 1 3.5 |
10. | 3 2 1 4.5 |
11. | 3 3 1 7.5 |
12. | 3 4 1 9.5 |
|-----------------------|
13. | 4 1 1 3.5 |
14. | 4 2 1 3.5 |
15. | 4 3 1 6.5 |
16. | 4 4 1 8.5 |
|-----------------------|
17. | 5 1 2 1 |
18. | 5 2 2 2 |
19. | 5 3 2 5 |
20. | 5 4 2 10 |
|-----------------------|
21. | 6 1 2 2 |
22. | 6 2 2 3 |
23. | 6 3 2 6 |
24. | 6 4 2 10 |
|-----------------------|
25. | 7 1 2 2 |
26. | 7 2 2 4 |
27. | 7 3 2 5 |
28. | 7 4 2 9 |
|-----------------------|
29. | 8 1 2 2 |
30. | 8 2 2 3 |
31. | 8 3 2 6 |
32. | 8 4 2 11 |
+-----------------------+
Now that we have reshaped the data we can move on to repeated measures anova.
Repeated measures anova
In anova parlance this design has both between-subject and within-subject effects, i.e., it is a mixed effects model. In particular this design is sometimes referred to as a split-plot factorial analysis of variance. In Stata, with the data in long form, we need to specify the error terms for both the between-subject and within-subject effects.
In general, the rule is that there is one single error term for all of the between-subject effects and a separate error term for each of the within-subject factors and for the interaction of within-subject factors.
Our model is relatively straight forward with only two error terms. The between-subject effect is treatment (trt) and its error term is subject nested in treatment (id | trt). The within-subject factor time time. Its error term is the residual error for the model.
Repeated measures anova have an assumption that the within-subject covariance structure is compound symmetric, also known as, exchangeable. With compound symmetry the variances at each time are expected to be equal and all of the covariances are expected to be equal to one another. If the within-subject covariance structure is not compound symmetric then the p-values obtained from the repeated measures anova may not accurately reflect the “true” probabilities. Stata lets you take the lack of compound symmetry into account by including the repeated() option in the anova command which computes p-values for conservative F-tests.
We will discuss covariance structures in greater depth later in the presentation.
Here is the anova command for our data.
anova y trt / id|trt time trt#time, repeated(time)
Number of obs = 32 R-squared = 0.9624
Root MSE = .712 Adj R-squared = 0.9352
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 233.375 13 17.9519231 35.41 0.0000
|
trt | 10.125 1 10.125 6.48 0.0438
id|trt | 9.375 6 1.5625
-----------+----------------------------------------------------
time | 194.5 3 64.8333333 127.89 0.0000
trt#time | 19.375 3 6.45833333 12.74 0.0001
|
Residual | 9.125 18 .506944444
-----------+----------------------------------------------------
Total | 242.5 31 7.82258065
Between-subjects error term: id|trt
Levels: 8 (6 df)
Lowest b.s.e. variable: id
Covariance pooled over: trt (for repeated variable)
Repeated variable: time
Huynh-Feldt epsilon = 0.9432
Greenhouse-Geisser epsilon = 0.5841
Box's conservative epsilon = 0.3333
------------ Prob > F ------------
Source | df F Regular H-F G-G Box
-----------+----------------------------------------------------
time | 3 127.89 0.0000 0.0000 0.0000 0.0000
trt#time | 3 12.74 0.0001 0.0002 0.0019 0.0118
Residual | 18
----------------------------------------------------------------
The treatment-by-time interaction is significant as are the two main-effects for treatment and time. The output includes the p-values for three different conservative F-tests: 1) Huynh-Feldt, 2) Greenhouse-Geisser and 3) Box’s conservative F. These values are indicators of the p-value is even if the data do not meet the compound symmetry assumption. We can view the pooled within-subject covariance matrix by listing the Srep matrix.
matrix list e(Srep)
symmetric e(Srep)[4,4]
c1 c2 c3 c4
r1 1.25
r2 .66666667 .66666667
r3 .58333333 .33333333 .5
r4 0 -.16666667 .16666667 .66666667
Inspection of the pooled within-subject covariance matrix casts doubt on the validity of the compound symmetry assumption. Fortunately, the p-values for the conservative F-test still indicate significant effects for the trt#time interaction and the time main effect.
Tests of simple effects
Since the treatment-by-time interaction is significant we should try to explain the interaction. One way to do this is through the use of test of simple effects. We will begin by looking at the effect of time at each treatment level.
The effect of time at each treatment
The simple effect of time has three degrees of freedom for each level of the treatment for a total of six degrees of freedom. This test of simple effects will use the residual error for the model as its error term. We will use the contrast command to do the test of simple effects.
contrast time@trt, effect
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df F P>F
-------------+----------------------------------
time@trt |
1 | 3 35.96 0.0000
2 | 3 104.67 0.0000
Joint | 6 70.32 0.0000
|
Residual | 18
------------------------------------------------
--------------------------------------------------------------------------------
| Contrast Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
time@trt |
(2 vs base) 1 | .25 .5034602 0.50 0.626 -.8077307 1.307731
(2 vs base) 2 | 1.25 .5034602 2.48 0.023 .1922693 2.307731
(3 vs base) 1 | 3.25 .5034602 6.46 0.000 2.192269 4.307731
(3 vs base) 2 | 3.75 .5034602 7.45 0.000 2.692269 4.807731
(4 vs base) 1 | 4.25 .5034602 8.44 0.000 3.192269 5.307731
(4 vs base) 2 | 8.25 .5034602 16.39 0.000 7.192269 9.307731
--------------------------------------------------------------------------------
Pairwise follow ups
Since each of the tests of simple effects involves four time points will follow up with pairwise comparisons using the margins command with the pwcompare option.
margins time, at(trt=1) pwcompare(effects) noestimcheck
Pairwise comparisons of predictive margins
Expression : Linear prediction, predict()
at : trt = 1
------------------------------------------------------------------------------
| Delta-method Unadjusted Unadjusted
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time |
2 vs 1 | .25 .5034602 0.50 0.619 -.736764 1.236764
3 vs 1 | 3.25 .5034602 6.46 0.000 2.263236 4.236764
4 vs 1 | 4.25 .5034602 8.44 0.000 3.263236 5.236764
3 vs 2 | 3 .5034602 5.96 0.000 2.013236 3.986764
4 vs 2 | 4 .5034602 7.95 0.000 3.013236 4.986764
4 vs 3 | 1 .5034602 1.99 0.047 .013236 1.986764
------------------------------------------------------------------------------
margins time, at(trt=2) pwcompare(effects) noestimcheck
Pairwise comparisons of predictive margins
Expression : Linear prediction, predict()
at : trt = 2
------------------------------------------------------------------------------
| Delta-method Unadjusted Unadjusted
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time |
2 vs 1 | 1.25 .5034602 2.48 0.013 .263236 2.236764
3 vs 1 | 3.75 .5034602 7.45 0.000 2.763236 4.736764
4 vs 1 | 8.25 .5034602 16.39 0.000 7.263236 9.236764
3 vs 2 | 2.5 .5034602 4.97 0.000 1.513236 3.486764
4 vs 2 | 7 .5034602 13.90 0.000 6.013236 7.986764
4 vs 3 | 4.5 .5034602 8.94 0.000 3.513236 5.486764
------------------------------------------------------------------------------
Anova with pooled error term
The tests of treatment at each tie point require the use of the pooled error. That is, pooling id | trt and the residual error. This is easily accomplished by removing id | trt from the anova command. Note that the residual degrees of freedom is now 24.
anova y trt##time
Number of obs = 32 R-squared = 0.9237
Root MSE = .877971 Adj R-squared = 0.9015
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 224 7 32 41.51 0.0000
|
trt | 10.125 1 10.125 13.14 0.0014
time | 194.5 3 64.8333333 84.11 0.0000
trt#time | 19.375 3 6.45833333 8.38 0.0006
|
Residual | 18.5 24 .770833333
-----------+----------------------------------------------------
Total | 242.5 31 7.82258065
The effect of treatment at each time
Now we can run the simple effects of treatment at each time, again using the contrast command. Since there are two levels of treatment at each time point there are a total of four degrees of freedom. Since each test is one degree of freedom, we do not have to do any follow up tests.
contrast trt@time, effect
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df F P>F
-------------+----------------------------------
trt@time |
1 | 1 16.22 0.0005
2 | 1 5.84 0.0237
3 | 1 10.38 0.0036
4 | 1 5.84 0.0237
Joint | 4 9.57 0.0001
|
Residual | 24
------------------------------------------------
--------------------------------------------------------------------------------
| Contrast Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
trt@time |
(2 vs base) 1 | -2.5 .6208194 -4.03 0.000 -3.781308 -1.218692
(2 vs base) 2 | -1.5 .6208194 -2.42 0.024 -2.781308 -.2186918
(2 vs base) 3 | -2 .6208194 -3.22 0.004 -3.281308 -.7186918
(2 vs base) 4 | 1.5 .6208194 2.42 0.024 .2186918 2.781308
--------------------------------------------------------------------------------
Graph of interaction
A graph of the interaction is always useful. We will use the margins command and marginsplot to produce the plot.
margins trt#time
Adjusted predictions Number of obs = 32
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
trt#time |
1 1 | 4.25 .4389856 9.68 0.000 3.389604 5.110396
1 2 | 4.5 .4389856 10.25 0.000 3.639604 5.360396
1 3 | 7.5 .4389856 17.08 0.000 6.639604 8.360396
1 4 | 8.5 .4389856 19.36 0.000 7.639604 9.360396
2 1 | 1.75 .4389856 3.99 0.000 .8896041 2.610396
2 2 | 3 .4389856 6.83 0.000 2.139604 3.860396
2 3 | 5.5 .4389856 12.53 0.000 4.639604 6.360396
2 4 | 10 .4389856 22.78 0.000 9.139604 10.8604
------------------------------------------------------------------------------
marginsplot, x(time)
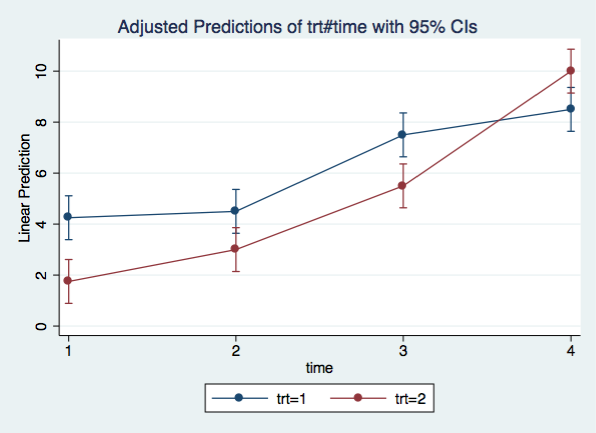
Disadvantages of repeated measures anova
Repeated measures anova suffers from several disadvantages among which are,
- does not allow unequal observations within subject
- user must determine correct error term for each effect
- assumes compound symmetry/exchangeable covariance structure
Repeated measures mixed model
An alternative to repeated measures anova is to run the analysis as a repeated measures mixed model. We will do this using the xtmixed command. Note that we do not have to specify the error terms, we only need to specify the name of the variable on which the data are repeated, in this case id. Here is what the mixed command looks like. Note, we use the reml option so the the results will be comparable to the anova results.
mixed y trt##time || id:, reml
Performing EM optimization ...
Performing gradient-based optimization:
Iteration 0: Log restricted-likelihood = -34.824381
Iteration 1: Log restricted-likelihood = -34.824379
Computing standard errors ...
Mixed-effects REML regression Number of obs = 32
Group variable: id Number of groups = 8
Obs per group:
min = 4
avg = 4.0
max = 4
Wald chi2(7) = 428.37
Log restricted-likelihood = -34.824379 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
2.trt | -2.5 .6208193 -4.03 0.000 -3.716783 -1.283217
|
time |
2 | .25 .5034603 0.50 0.619 -.736764 1.236764
3 | 3.25 .5034603 6.46 0.000 2.263236 4.236764
4 | 4.25 .5034603 8.44 0.000 3.263236 5.236764
|
trt#time |
2 2 | 1 .7120004 1.40 0.160 -.3954951 2.395495
2 3 | .5 .7120004 0.70 0.483 -.8954951 1.895495
2 4 | 4 .7120004 5.62 0.000 2.604505 5.395495
|
_cons | 4.25 .4389855 9.68 0.000 3.389604 5.110396
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects parameters | Estimate Std. err. [95% conf. interval]
-----------------------------+------------------------------------------------
id: Identity |
var(_cons) | .2638887 .2294499 .0480071 1.450562
-----------------------------+------------------------------------------------
var(Residual) | .5069445 .1689815 .2637707 .9743036
------------------------------------------------------------------------------
LR test vs. linear model: chibar2(01) = 3.30 Prob >= chibar2 = 0.0346
In addition to the estimates of the fixed effects we get two random effects. These are the variance of the intercepts and the residual variance which correspond to the between-subject and within-subject variances respectively.
The mixed command produces estimates for each term in the model individually. To get joint tests (multi degree of freedom) of the interaction and main effects we will use the contrast command.
contrast trt##time
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df chi2 P>chi2
-------------+----------------------------------
y |
trt | 1 6.48 0.0109
|
time | 3 383.67 0.0000
|
trt#time | 3 38.22 0.0000
------------------------------------------------
Graph of interaction
Let’s graph the interaction using the same margins and marginsplot commands as before.
margins trt#time
Adjusted predictions Number of obs = 32
Expression : Linear prediction, fixed portion, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
trt#time |
1 1 | 4.25 .4389855 9.68 0.000 3.389604 5.110396
1 2 | 4.5 .4389855 10.25 0.000 3.639604 5.360396
1 3 | 7.5 .4389855 17.08 0.000 6.639604 8.360396
1 4 | 8.5 .4389855 19.36 0.000 7.639604 9.360396
2 1 | 1.75 .4389855 3.99 0.000 .8896042 2.610396
2 2 | 3 .4389855 6.83 0.000 2.139604 3.860396
2 3 | 5.5 .4389855 12.53 0.000 4.639604 6.360396
2 4 | 10 .4389855 22.78 0.000 9.139604 10.8604
------------------------------------------------------------------------------
marginsplot, x(time)
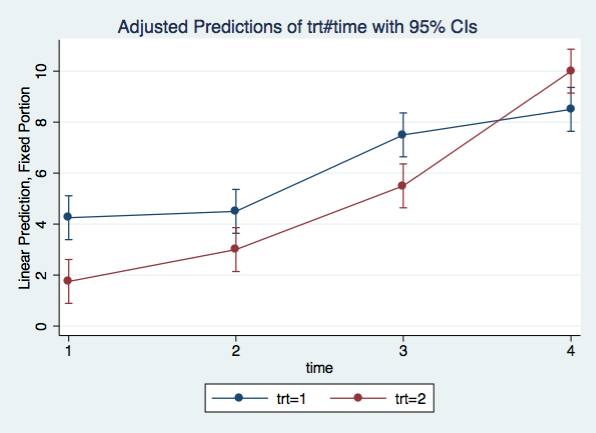
Test of simple effects
Once again, we can use tests of simple effects to understand the significant interaction.
time at each treatment
contrast time@trt, effect
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df chi2 P>chi2
-------------+----------------------------------
y |
time@trt |
1 | 3 107.88 0.0000
2 | 3 314.01 0.0000
Joint | 6 421.89 0.0000
------------------------------------------------
--------------------------------------------------------------------------------
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
---------------+----------------------------------------------------------------
y |
time@trt |
(2 vs base) 1 | .25 .5034603 0.50 0.619 -.736764 1.236764
(2 vs base) 2 | 1.25 .5034603 2.48 0.013 .263236 2.236764
(3 vs base) 1 | 3.25 .5034603 6.46 0.000 2.263236 4.236764
(3 vs base) 2 | 3.75 .5034603 7.45 0.000 2.763236 4.736764
(4 vs base) 1 | 4.25 .5034603 8.44 0.000 3.263236 5.236764
(4 vs base) 2 | 8.25 .5034603 16.39 0.000 7.263236 9.236764
--------------------------------------------------------------------------------
Since each of these tests of simple effects uses three degrees of freedom, we will followup using pairwise comparisons.
margins time, at(trt=1) pwcompare(effects)
Pairwise comparisons of adjusted predictions
Expression : Linear prediction, fixed portion, predict()
at : trt = 1
------------------------------------------------------------------------------
| Delta-method Unadjusted Unadjusted
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time |
2 vs 1 | .25 .5034603 0.50 0.619 -.736764 1.236764
3 vs 1 | 3.25 .5034603 6.46 0.000 2.263236 4.236764
4 vs 1 | 4.25 .5034603 8.44 0.000 3.263236 5.236764
3 vs 2 | 3 .5034603 5.96 0.000 2.013236 3.986764
4 vs 2 | 4 .5034603 7.95 0.000 3.013236 4.986764
4 vs 3 | 1 .5034603 1.99 0.047 .013236 1.986764
------------------------------------------------------------------------------
margins time, at(trt=2) pwcompare(effects)
Pairwise comparisons of adjusted predictions
Expression : Linear prediction, fixed portion, predict()
at : trt = 2
------------------------------------------------------------------------------
| Delta-method Unadjusted Unadjusted
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
time |
2 vs 1 | 1.25 .5034603 2.48 0.013 .263236 2.236764
3 vs 1 | 3.75 .5034603 7.45 0.000 2.763236 4.736764
4 vs 1 | 8.25 .5034603 16.39 0.000 7.263236 9.236764
3 vs 2 | 2.5 .5034603 4.97 0.000 1.513236 3.486764
4 vs 2 | 7 .5034603 13.90 0.000 6.013236 7.986764
4 vs 3 | 4.5 .5034603 8.94 0.000 3.513236 5.486764
------------------------------------------------------------------------------
treatment at each time
contrast trt@time, effect
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df chi2 P>chi2
-------------+----------------------------------
y |
trt@time |
1 | 1 16.22 0.0001
2 | 1 5.84 0.0157
3 | 1 10.38 0.0013
4 | 1 5.84 0.0157
Joint | 4 44.70 0.0000
------------------------------------------------
--------------------------------------------------------------------------------
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
---------------+----------------------------------------------------------------
y |
trt@time |
(2 vs base) 1 | -2.5 .6208193 -4.03 0.000 -3.716783 -1.283217
(2 vs base) 2 | -1.5 .6208193 -2.42 0.016 -2.716783 -.2832165
(2 vs base) 3 | -2 .6208193 -3.22 0.001 -3.216783 -.7832165
(2 vs base) 4 | 1.5 .6208193 2.42 0.016 .2832165 2.716783
--------------------------------------------------------------------------------
Post-hoc test of trends
Another way of looking at these results would be to look at the trend over time for each of the two groups. We do this by using the p. contrast operator which gives use coefficients of orthogonal polynomials. We keep the @ operator that we used in the tests of simple effects to give the results by treatment.
contrast p.time@trt, effect
Contrasts of marginal linear predictions
Margins : asbalanced
--------------------------------------------------
| df chi2 P>chi2
---------------+----------------------------------
y |
time@trt |
(linear) 1 | 1 97.87 0.0000
(linear) 2 | 1 292.96 0.0000
(quadratic) 1 | 1 1.11 0.2922
(quadratic) 2 | 1 20.84 0.0000
(cubic) 1 | 1 8.90 0.0028
(cubic) 2 | 1 0.22 0.6376
Joint | 6 421.89 0.0000
--------------------------------------------------
--------------------------------------------------------------------------------
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
---------------+----------------------------------------------------------------
y |
time@trt |
(linear) 1 | 1.760904 .1780001 9.89 0.000 1.41203 2.109777
(linear) 2 | 3.046643 .1780001 17.12 0.000 2.697769 3.395516
(quadratic) 1 | .1875 .1780001 1.05 0.292 -.1613738 .5363738
(quadratic) 2 | .8125 .1780001 4.56 0.000 .4636262 1.161374
(cubic) 1 | -.5310661 .1780001 -2.98 0.003 -.8799399 -.1821924
(cubic) 2 | .0838525 .1780001 0.47 0.638 -.2650212 .4327263
--------------------------------------------------------------------------------
The results show a significant linear trend for both treatment 1 and treatment 2. Treatment 2 has a significant quadratic trend while treatment 1 has a significant cubic trend.
Post-hoc test of partial interaction
Yet another alternative is to look at the partial interactions between treatment and time. We are going to look at the two treatments and two time points for each test. To understand our tests of partial interaction it helps to view the graph of the interaction. The first test looks at the two lines between time 1 and time 2. The next test looks at the lines between time 2 and time 3. And, the final test looks at the two lines between time 3 and time 4. For each of the partial interactions we are testing if the interaction among the four cells is significant. The way to set up the tests of partial interaction is to use the a. (adjacent) contrast operator along with the # for interaction. The explanation is much more complex than the concept.
contrast a.time#trt
Contrasts of marginal linear predictions
Margins : asbalanced
-----------------------------------------------------
| df chi2 P>chi2
------------------+----------------------------------
y |
time#trt |
(1 vs 2) (joint) | 1 1.97 0.1602
(2 vs 3) (joint) | 1 0.49 0.4825
(3 vs 4) (joint) | 1 24.16 0.0000
Joint | 3 38.22 0.0000
-----------------------------------------------------
The results indicate that there is no interaction between time 1 and time 2 or between time 2 and time 3. However, there is an interaction between times 3 and 4.
Within-subject covariance structures
We stated earlier that we would get back to the topic of within-subject covariance structures. So, let’s look at several of the possible within-subject covariance structures.
Independence
This covariance structure treats the repeated effects as being totally independent, just as if the design were between-subjects.
σ2 0 σ2 0 0 σ2 0 0 0 σ2
Compound symmetry/exchangeable
Repeated measures anova assumes that the within-subject covariance structure has compound symmetry. There is a single variance (σ2) for all 3 of the time points and there is a single covariance (σ1) for each of the pairs of trials. This is illustrated below. Stata calls this covariance structure exchangeable.
σ2 σ1 σ2 σ1 σ1 σ2 σ1 σ1 σ1 σ2
Unstructured
For the unstructured covariance each time point has its own variance (e.g. σ12 is the variance of time 1) and each pair of time points has its own covariance (e.g., σ21 is the covariance of time 1 and time 2). This is the type of covariance structure is found multivariate analysis of variance (manova).
σ12 σ21 σ22 σ31 σ32 σ32 σ41 σ42 σ43 σ42
The downside to using unstructured covariance is the larger number of parameters being estimated.
Autoregressive
Another common covariance structure which is frequently observed in repeated measures data is an autoregressive structure, which recognizes that observations which are more proximate are more correlated than measures that are more distant. Below is an example of an autoregressive 1 covariance matrix.
σ2 σr σ2 σr2 σr σ2 σr3 σr2 σr σ2
It is also possible to have autoregressive 2 or 3 type structures. In addition to the covariance structures shown above, Stata also offers the following covariance structures: moving average, banded, toeplitz and exponential.
Example with unstructured covariance
After inspecting our within-subject covariance matrix, we have decided to use unstructured within-subject covariance.
mixed y trt##time || id:, noconst residuals(unstr, t(time)) reml
Obtaining starting values by EM:
Performing gradient-based optimization:
Iteration 0: log restricted-likelihood = -36.476305 (not concave)
Iteration 1: log restricted-likelihood = -32.170858 (not concave)
Iteration 2: log restricted-likelihood = -30.790578
Iteration 3: log restricted-likelihood = -30.075124
Iteration 4: log restricted-likelihood = -29.820951
Iteration 5: log restricted-likelihood = -29.819621
Iteration 6: log restricted-likelihood = -29.81962
Computing standard errors:
Mixed-effects REML regression Number of obs = 32
Group variable: id Number of groups = 8
Obs per group: min = 4
avg = 4.0
max = 4
Wald chi2(7) = 247.94
Log restricted-likelihood = -29.81962 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
2.trt | -2.5 .7905694 -3.16 0.002 -4.049487 -.9505125
|
time |
2 | .25 .3818814 0.65 0.513 -.4984737 .9984737
3 | 3.25 .3818812 8.51 0.000 2.501527 3.998473
4 | 4.25 .6922186 6.14 0.000 2.893276 5.606724
|
trt#time |
2 2 | 1 .5400618 1.85 0.064 -.0585017 2.058502
2 3 | .5 .5400616 0.93 0.355 -.5585013 1.558501
2 4 | 4 .978945 4.09 0.000 2.081303 5.918697
|
_cons | 4.25 .559017 7.60 0.000 3.154347 5.345653
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: (empty) |
-----------------------------+------------------------------------------------
Residual: Unstructured |
var(e1) | 1.25 .721688 .4031515 3.875713
var(e2) | .6666668 .3849007 .215014 2.067049
var(e3) | .4999998 .2886746 .1612609 1.550281
var(e4) | .6666667 .3849003 .2150142 2.067047
cov(e1,e2) | .6666666 .4614796 -.2378169 1.57115
cov(e1,e3) | .5833333 .4010976 -.2028035 1.36947
cov(e1,e4) | 1.76e-08 .372678 -.7304354 .7304354
cov(e2,e3) | .3333334 .2721656 -.2001015 .8667682
cov(e2,e4) | -.1666667 .2805416 -.7165181 .3831847
cov(e3,e4) | .1666665 .245327 -.3141656 .6474986
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(9) = 13.31 Prob > chi2 = 0.1489
Note: The reported degrees of freedom assumes the null hypothesis is not on the boundary of
the parameter space. If this is not true, then the reported test is conservative.
Here is the joint (multi-degree of freedom) test for the interaction.
contrast time#trt, effect
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df chi2 P>chi2
-------------+----------------------------------
y |
trt#time | 3 35.58 0.0000
------------------------------------------------
tests of simple effects: trt@time
Since the interaction is statistically significant we will follow up with a test of simple effects of time at each treatment.
contrast time@trt, effect
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df chi2 P>chi2
-------------+----------------------------------
y |
time@trt |
1 | 3 100.99 0.0000
2 | 3 146.96 0.0000
Joint | 6 247.94 0.0000
------------------------------------------------
--------------------------------------------------------------------------------
| Contrast Std. Err. z P>|z| [95% Conf. Interval]
---------------+----------------------------------------------------------------
y |
time@trt |
(2 vs base) 1 | .25 .3818814 0.65 0.513 -.4984737 .9984737
(2 vs base) 2 | 1.25 .3818814 3.27 0.001 .5015263 1.998474
(3 vs base) 1 | 3.25 .3818812 8.51 0.000 2.501527 3.998473
(3 vs base) 2 | 3.75 .3818812 9.82 0.000 3.001527 4.498473
(4 vs base) 1 | 4.25 .6922186 6.14 0.000 2.893276 5.606724
(4 vs base) 2 | 8.25 .6922186 11.92 0.000 6.893276 9.606724
--------------------------------------------------------------------------------
Growth models
Linear growth model
It is also possible to treat time as a continuous variable, in which case, the model would be considered to be a linear growth model. To simplify the interpretation of the intercept we are going to start time at zero instead of one. We do this by creating a new variable ctime which is time – 1. We need to let mixed know that we are treating ctime as continuous by using the c. prefix.
Note, when using a mixed model it is not necessary for each subject to be measured at the same time points although in our case they are all measured at the same four time points.
Here is our linear growth model.
generate ctime = time - 1
mixed y trt##c.ctime || id:
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -46.500622
Iteration 1: log likelihood = -46.470323
Iteration 2: log likelihood = -46.470167
Iteration 3: log likelihood = -46.470167
Computing standard errors:
Mixed-effects ML regression Number of obs = 32
Group variable: id Number of groups = 8
Obs per group: min = 4
avg = 4.0
max = 4
Wald chi2(3) = 199.80
Log likelihood = -46.470167 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
2.trt | -2.85 .6161878 -4.63 0.000 -4.057706 -1.642294
ctime | 1.575 .2276465 6.92 0.000 1.128821 2.021179
|
trt#c.ctime |
2 | 1.15 .3219408 3.57 0.000 .5190076 1.780992
|
_cons | 3.825 .4357106 8.78 0.000 2.971023 4.678977
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Identity |
var(_cons) | .0338535 .1644761 2.48e-06 462.531
-----------------------------+------------------------------------------------
var(Residual) | 1.036459 .2991998 .5886153 1.825041
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 0.05 Prob >= chibar2 = 0.4149
As you can see the interaction term is still statistically significant. You need to be careful about interpreting trt and ctime as main effects in the anova sense. The ctime coefficient is the slope of y on ctime in the reference group. While the coefficient for trt is the difference in the two groups when ctime is zero.
Simple slopes
We can use the margins command with the dydx option to get the slopes of each of the two treatment groups. Note that the slope for trt 1 is the same as the coefficient for ctime above.
margins trt, dydx(ctime)
Average marginal effects Number of obs = 32
Expression : Linear prediction, fixed portion, predict()
dy/dx w.r.t. : ctime
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ctime |
trt |
1 | 1.575 .2276465 6.92 0.000 1.128821 2.021179
2 | 2.725 .2276465 11.97 0.000 2.278821 3.171179
------------------------------------------------------------------------------
We can also test the difference in the slopes using the margins command with reference group coding using the r. contrast operator. It is not really necessary to do this because we already know that the difference in slopes is significant from the interaction term above. In fact, if you take the z-value for the interaction (3.57) and square it (12.7449), you get the chi-square shown below to within rounding error.
margins r.trt, dydx(ctime)
Contrasts of average marginal effects
Expression : Linear prediction, fixed portion, predict()
dy/dx w.r.t. : ctime
------------------------------------------------
| df chi2 P>chi2
-------------+----------------------------------
ctime |
trt | 1 12.76 0.0004
------------------------------------------------
--------------------------------------------------------------
| Contrast Delta-method
| dy/dx Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
ctime |
trt |
(2 vs 1) | 1.15 .3219408 .5190076 1.780992
--------------------------------------------------------------
Graphing the interaction
We can visualize the simple slopes by graphing the interaction using a variation of margins with the at() option along with the marginsplot command.
margins trt, at(ctime=(0(1)3)) vsquish
Adjusted predictions Number of obs = 32
Expression : Linear prediction, fixed portion, predict()
1._at : ctime = 0
2._at : ctime = 1
3._at : ctime = 2
4._at : ctime = 3
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at#trt |
1 1 | 3.825 .4357106 8.78 0.000 2.971023 4.678977
1 2 | .975 .4357106 2.24 0.025 .121023 1.828977
2 1 | 5.4 .2935946 18.39 0.000 4.824565 5.975435
2 2 | 3.7 .2935946 12.60 0.000 3.124565 4.275435
3 1 | 6.975 .2935946 23.76 0.000 6.399565 7.550435
3 2 | 6.425 .2935946 21.88 0.000 5.849565 7.000435
4 1 | 8.55 .4357106 19.62 0.000 7.696023 9.403977
4 2 | 9.15 .4357106 21.00 0.000 8.296023 10.00398
------------------------------------------------------------------------------
marginsplot, x(ctime)
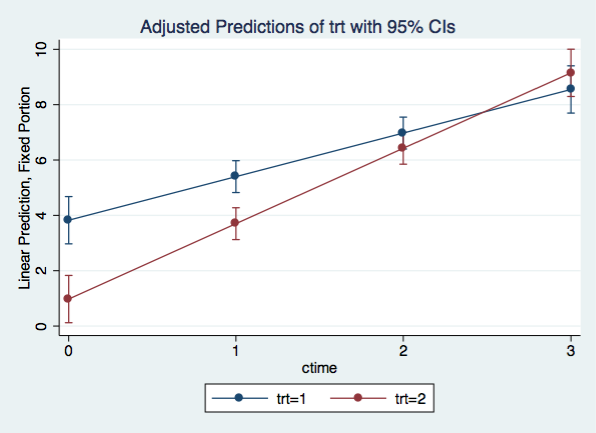
Quadratic growth model
We do not have to restrict ourselves to a linear relation over time. We can easily include a quadratic effect by repeating c.ctime term in our model.
mixed y trt##c.ctime##c.ctime || id:
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -39.356298
Iteration 1: log likelihood = -39.356273
Iteration 2: log likelihood = -39.356273
Computing standard errors:
Mixed-effects ML regression Number of obs = 32
Group variable: id Number of groups = 8
Obs per group: min = 4
avg = 4.0
max = 4
Wald chi2(5) = 373.88
Log likelihood = -39.356273 Prob > chi2 = 0.0000
-------------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
--------------------+----------------------------------------------------------------
2.trt | -2.225 .5890715 -3.78 0.000 -3.379559 -1.070441
ctime | 1.0125 .5923778 1.71 0.087 -.1485391 2.173539
|
trt#c.ctime |
2 | -.725 .8377487 -0.87 0.387 -2.366957 .9169573
|
c.ctime#c.ctime | .1875 .1892281 0.99 0.322 -.1833804 .5583804
|
trt#c.ctime#c.ctime |
2 | .625 .267609 2.34 0.020 .100496 1.149504
|
_cons | 4.0125 .4165364 9.63 0.000 3.196104 4.828896
-------------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Identity |
var(_cons) | .1497396 .1522079 .0204223 1.097916
-----------------------------+------------------------------------------------
var(Residual) | .5729167 .1653868 .3253649 1.008816
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 1.71 Prob >= chibar2 = 0.0958
Graphing the quadratic model
We can graph the quadratic model using the same margins and marginsplot commands that we used for the linear model
margins trt, at(ctime=(0(1)3)) vsquish
Adjusted predictions Number of obs = 32
Expression : Linear prediction, fixed portion, predict()
1._at : ctime = 0
2._at : ctime = 1
3._at : ctime = 2
4._at : ctime = 3
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at#trt |
1 1 | 4.0125 .4165364 9.63 0.000 3.196104 4.828896
1 2 | 1.7875 .4165364 4.29 0.000 .9711036 2.603896
2 1 | 5.2125 .3408973 15.29 0.000 4.544354 5.880646
2 2 | 2.8875 .3408973 8.47 0.000 2.219354 3.555646
3 1 | 6.7875 .3408973 19.91 0.000 6.119354 7.455646
3 2 | 5.6125 .3408973 16.46 0.000 4.944354 6.280646
4 1 | 8.7375 .4165364 20.98 0.000 7.921104 9.553896
4 2 | 9.9625 .4165364 23.92 0.000 9.146104 10.7789
------------------------------------------------------------------------------
marginsplot, x(ctime)
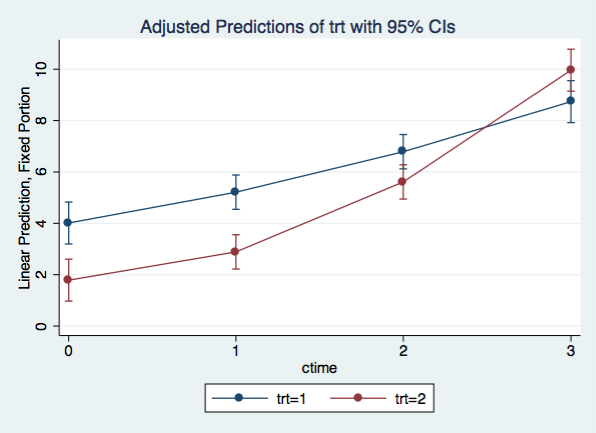
Cubic growth model
If we add an additional ctime to our quadratic growth model, we get a cubic growth model.
mixed y trt##c.ctime##c.ctime##c.ctime || id:
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log likelihood = -34.436022
Iteration 1: log likelihood = -34.436022
Computing standard errors:
Mixed-effects ML regression Number of obs = 32
Group variable: id Number of groups = 8
Obs per group: min = 4
avg = 4.0
max = 4
Wald chi2(7) = 571.16
Log likelihood = -34.436022 Prob > chi2 = 0.0000
---------------------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
----------------------------+----------------------------------------------------------------
2.trt | -2.5 .5376454 -4.65 0.000 -3.553766 -1.446234
ctime | -2.708333 1.182953 -2.29 0.022 -5.026879 -.3897881
|
trt#c.ctime |
2 | 3.583333 1.672948 2.14 0.032 .3044152 6.862251
|
c.ctime#c.ctime | 3.75 1.045514 3.59 0.000 1.700831 5.799169
|
trt#c.ctime#c.ctime |
2 | -3.5 1.47858 -2.37 0.018 -6.397963 -.6020372
|
c.ctime#c.ctime#c.ctime | -.7916667 .2297971 -3.45 0.001 -1.242061 -.3412726
|
trt#c.ctime#c.ctime#c.ctime |
2 | .9166667 .3249822 2.82 0.005 .2797133 1.55362
|
_cons | 4.25 .3801727 11.18 0.000 3.504875 4.995125
---------------------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Identity |
var(_cons) | .1979168 .1490322 .0452401 .8658471
-----------------------------+------------------------------------------------
var(Residual) | .3802083 .1097567 .215924 .6694872
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 4.41 Prob >= chibar2 = 0.0179
Graphing the cubic model
margins trt, at(ctime=(0(1)3)) vsquish
Adjusted predictions Number of obs = 32
Expression : Linear prediction, fixed portion, predict()
1._at : ctime = 0
2._at : ctime = 1
3._at : ctime = 2
4._at : ctime = 3
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at#trt |
1 1 | 4.25 .3801727 11.18 0.000 3.504875 4.995125
1 2 | 1.75 .3801727 4.60 0.000 1.004875 2.495125
2 1 | 4.5 .3801727 11.84 0.000 3.754875 5.245125
2 2 | 3 .3801727 7.89 0.000 2.254875 3.745125
3 1 | 7.5 .3801727 19.73 0.000 6.754875 8.245125
3 2 | 5.5 .3801727 14.47 0.000 4.754875 6.245125
4 1 | 8.5 .3801727 22.36 0.000 7.754875 9.245125
4 2 | 10 .3801727 26.30 0.000 9.254875 10.74512
------------------------------------------------------------------------------
marginsplot, x(ctime)
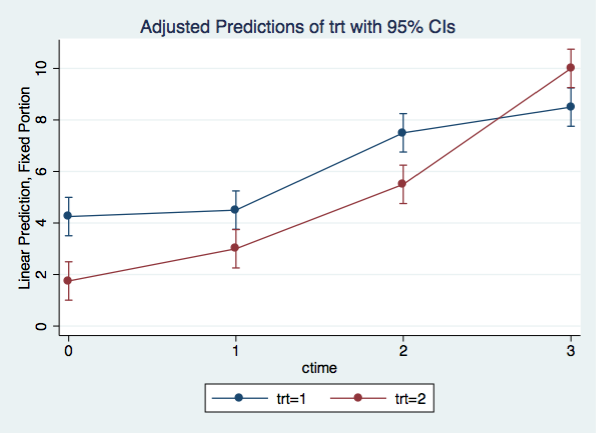
Slopes for each treatment and time point
With a slight variation to the margins command, we can get the slopes for each treatment group at each time point.
margins trt, dydx(ctime) at(ctime=(0(1)3)) vsquish
Conditional marginal effects Number of obs = 32
Expression : Linear prediction, fixed portion, predict()
dy/dx w.r.t. : ctime
1._at : ctime = 0
2._at : ctime = 1
3._at : ctime = 2
4._at : ctime = 3
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ctime |
_at#trt |
1 1 | -2.708333 1.182953 -2.29 0.022 -5.026879 -.3897881
1 2 | .875 1.182953 0.74 0.459 -1.443545 3.193545
2 1 | 2.416667 .3633411 6.65 0.000 1.704531 3.128802
2 2 | 1.75 .3633411 4.82 0.000 1.037864 2.462136
3 1 | 2.791667 .3633411 7.68 0.000 2.079531 3.503802
3 2 | 3.375 .3633411 9.29 0.000 2.662864 4.087136
4 1 | -1.583333 1.182953 -1.34 0.181 -3.901879 .7352119
4 2 | 5.75 1.182953 4.86 0.000 3.431455 8.068545
------------------------------------------------------------------------------
You will note that for treatment 2 the slopes just keep getting steeper and steeper, while for treatment 1, the slopes go up and then back down.
Advantages and disadvantages of mixed models
There are both advantages and disadvantages to using mixed models but on the whole mixed models are more flexible and have more advantages than disadvantages.
Advantages
- automatically computes correct standard errors for each effect
- allows unbalance or missing observations within-subject
- allows unequal time intervals
- allows various within-subject covariance structures
- allows time to be treated as categorical or continuous
Disadvantages
- mixed reports results as chi-square; the p-values are appropriate for large samples and are biased downwards in small samples