The purpose of this seminar is to give users an introduction to analyzing multinomial logistic models using Stata. In addition to the built-in Stata commands we will be demonstrating the use of a number on user-written ado’s, in particular, listcoef, fitstat, prchange, prtab, etc. To find out more about these programs or to download them type search followed by the program name in the Stata command window (example: search listcoef). Or, you can download the complete spostado package by typing the following in the Stata command window:
net from http://www.indiana.edu/~jslsoc/stata/ net install spostado
These add-on programs ease the running and interpretation of ordinal logistic models.
Binary Response Variable Example
Let’s begin with an example using a binary response variable. We will see that the results of an multinomial logistic model are exactly the same as for a traditional logistic model.
use https://stats.idre.ucla.edu/stat/stata/seminars/stata_BeyondBinaryLogistic/honors2, clear
logit honors female
Iteration 0: log likelihood = -115.64441
Iteration 1: log likelihood = -113.68907
Iteration 2: log likelihood = -113.67691
Iteration 3: log likelihood = -113.6769
Logit estimates Number of obs = 200
LR chi2(1) = 3.94
Prob > chi2 = 0.0473
Log likelihood = -113.6769 Pseudo R2 = 0.0170
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | .6513707 .3336752 1.95 0.051 -.0026207 1.305362
_cons | -1.400088 .2631619 -5.32 0.000 -1.915876 -.8842998
------------------------------------------------------------------------------
mlogit honors female
Iteration 0: log likelihood = -115.64441
Iteration 1: log likelihood = -113.68907
Iteration 2: log likelihood = -113.67691
Iteration 3: log likelihood = -113.6769
Multinomial logistic regression Number of obs = 200
LR chi2(1) = 3.94
Prob > chi2 = 0.0473
Log likelihood = -113.6769 Pseudo R2 = 0.0170
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1 |
female | .6513707 .3336752 1.95 0.051 -.0026207 1.305362
_cons | -1.400088 .2631619 -5.32 0.000 -1.915876 -.8842998
------------------------------------------------------------------------------
(Outcome honors==0 is the comparison group)
predict p0 p1
(option p assumed; predicted probabilities)
list female honors p0 p1 in 1/20, nolabel
+---------------------------------------+
| female honors p0 p1 |
|---------------------------------------|
1. | 1 0 .6788991 .3211009 |
2. | 0 0 .8021978 .1978022 |
3. | 0 0 .8021978 .1978022 |
4. | 1 1 .6788991 .3211009 |
5. | 1 1 .6788991 .3211009 |
|---------------------------------------|
6. | 0 0 .8021978 .1978022 |
7. | 1 0 .6788991 .3211009 |
8. | 1 0 .6788991 .3211009 |
9. | 1 0 .6788991 .3211009 |
10. | 1 0 .6788991 .3211009 |
|---------------------------------------|
11. | 1 1 .6788991 .3211009 |
12. | 0 0 .8021978 .1978022 |
13. | 0 0 .8021978 .1978022 |
14. | 1 0 .6788991 .3211009 |
15. | 1 0 .6788991 .3211009 |
|---------------------------------------|
16. | 1 0 .6788991 .3211009 |
17. | 0 0 .8021978 .1978022 |
18. | 1 0 .6788991 .3211009 |
19. | 1 1 .6788991 .3211009 |
20. | 1 0 .6788991 .3211009 |
+---------------------------------------+
3-Category Response Variable Example
codebook prog
prog type of program
----------------------------------------------------------------------------------------------------------
type: numeric (float)
label: sel
range: [1,3] units: 1
unique values: 3 missing .: 0/200
tabulation: Freq. Numeric Label
45 1 general
105 2 academic
50 3 vocation
mlogit prog honors
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -196.10509
Iteration 2: log likelihood = -196.02441
Iteration 3: log likelihood = -196.02417
Multinomial logistic regression Number of obs = 200
LR chi2(2) = 16.15
Prob > chi2 = 0.0003
Log likelihood = -196.02417 Pseudo R2 = 0.0396
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
honors | -1.206168 .4577753 -2.63 0.008 -2.103391 -.3089452
_cons | -.5368011 .2042068 -2.63 0.009 -.937039 -.1365632
-------------+----------------------------------------------------------------
vocation |
honors | -1.506922 .479347 -3.14 0.002 -2.446425 -.5674196
_cons | -.3901976 .1952227 -2.00 0.046 -.772827 -.0075682
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
mlogit, rrr /* relative risk ratios */
Multinomial logistic regression Number of obs = 200
LR chi2(2) = 16.15
Prob > chi2 = 0.0003
Log likelihood = -196.02417 Pseudo R2 = 0.0396
------------------------------------------------------------------------------
prog | RRR Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
honors | .2993421 .1370314 -2.63 0.008 .1220419 .734221
-------------+----------------------------------------------------------------
vocation |
honors | .2215909 .1062189 -3.14 0.002 .0866026 .5669866
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
Next, we look at some of the Long & Freese utilities.
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: honors (sd= .44)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.30075 0.502 0.615 1.3509 1.1423
general -academic | -1.20617 -2.635 0.008 0.2993 0.5865
vocation-general | -0.30075 -0.502 0.615 0.7403 0.8754
vocation-academic | -1.50692 -3.144 0.002 0.2216 0.5134
academic-general | 1.20617 2.635 0.008 3.3407 1.7052
academic-vocation | 1.50692 3.144 0.002 4.5128 1.9478
----------------------------------------------------------------
listcoef, percent
mlogit (N=200): Percentage Change in the Odds of prog
Variable: honors (sd= .44)
Odds comparing|
Group 1 vs Group 2| b z P>|z| % %StdX
------------------+---------------------------------------------
general -vocation | 0.30075 0.502 0.615 35.1 14.2
general -academic | -1.20617 -2.635 0.008 -70.1 -41.4
vocation-general | -0.30075 -0.502 0.615 -26.0 -12.5
vocation-academic | -1.50692 -3.144 0.002 -77.8 -48.7
academic-general | 1.20617 2.635 0.008 234.1 70.5
academic-vocation | 1.50692 3.144 0.002 351.3 94.8
----------------------------------------------------------------
fitstat, saving(M1)
Measures of Fit for mlogit of prog
Log-Lik Intercept Only: -204.097 Log-Lik Full Model: -196.024
D(196): 392.048 LR(2): 16.145
Prob > LR: 0.000
McFadden's R2: 0.040 McFadden's Adj R2: 0.020
Maximum Likelihood R2: 0.078 Cragg & Uhler's R2: 0.089
Count R2: 0.525 Adj Count R2: 0.000
AIC: 2.000 AIC*n: 400.048
BIC: -646.422 BIC': -5.548
prchange
mlogit: Changes in Predicted Probabilities for prog
honors
Avg|Chg| general vocation academic
0->1 .20836007 -.12642793 -.18611217 .31254011
general vocation academic
Pr(y|x) .2260426 .24168304 .53227437
honors
x= .265
sd(x)= .442441
prtab honors
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
----------------------
honors | Prediction
----------+-----------
0 | 0.2585
1 | 0.1321
----------------------
Predicted probability of outcome 3 (vocation)
----------------------
honors | Prediction
----------+-----------
0 | 0.2993
1 | 0.1132
----------------------
Predicted probability of outcome 2 (academic)
----------------------
honors | Prediction
----------+-----------
0 | 0.4422
1 | 0.7547
----------------------
honors
x= .265
predict p1 p2 p3
(option p assumed; predicted probabilities)
list honors prog p1 p2 p3 in 1/20, nolabel
+------------------------------------------------+
| honors prog p1 p2 p3 |
|------------------------------------------------|
1. | 0 1 .2585034 .4421769 .2993197 |
2. | 0 3 .2585034 .4421769 .2993197 |
3. | 0 1 .2585034 .4421769 .2993197 |
4. | 0 3 .2585034 .4421769 .2993197 |
5. | 0 2 .2585034 .4421769 .2993197 |
|------------------------------------------------|
6. | 0 2 .2585034 .4421769 .2993197 |
7. | 0 1 .2585034 .4421769 .2993197 |
8. | 0 2 .2585034 .4421769 .2993197 |
9. | 0 1 .2585034 .4421769 .2993197 |
10. | 0 2 .2585034 .4421769 .2993197 |
|------------------------------------------------|
11. | 0 3 .2585034 .4421769 .2993197 |
12. | 1 2 .1320755 .754717 .1132075 |
13. | 1 2 .1320755 .754717 .1132075 |
14. | 1 2 .1320755 .754717 .1132075 |
15. | 0 2 .2585034 .4421769 .2993197 |
|------------------------------------------------|
16. | 0 1 .2585034 .4421769 .2993197 |
17. | 0 2 .2585034 .4421769 .2993197 |
18. | 0 1 .2585034 .4421769 .2993197 |
19. | 1 2 .1320755 .754717 .1132075 |
20. | 0 1 .2585034 .4421769 .2993197 |
+------------------------------------------------+
drop p1 p2 p3
An Example Using a Continuous Predictor
mlogit prog science
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -196.49276
Iteration 2: log likelihood = -196.32825
Iteration 3: log likelihood = -196.32807
Multinomial logistic regression Number of obs = 200
LR chi2(2) = 15.54
Prob > chi2 = 0.0004
Log likelihood = -196.32807 Pseudo R2 = 0.0381
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
science | -.0151248 .0188094 -0.80 0.421 -.0519906 .021741
_cons | -.0437733 1.010225 -0.04 0.965 -2.023778 1.936231
-------------+----------------------------------------------------------------
vocation |
science | -.0708203 .0189509 -3.74 0.000 -.1079633 -.0336774
_cons | 2.837688 .956162 2.97 0.003 .9636445 4.711731
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
test science
( 1) [general]science = 0
( 2) [vocation]science = 0
chi2( 2) = 14.16
Prob > chi2 = 0.0008
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: science (sd= 9.9)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.05570 2.540 0.011 1.0573 1.7357
general -academic | -0.01512 -0.804 0.421 0.9850 0.8609
vocation-general | -0.05570 -2.540 0.011 0.9458 0.5761
vocation-academic | -0.07082 -3.737 0.000 0.9316 0.4960
academic-general | 0.01512 0.804 0.421 1.0152 1.1615
academic-vocation | 0.07082 3.737 0.000 1.0734 2.0161
----------------------------------------------------------------
fitstat, using(M1)
Measures of Fit for mlogit of prog
Current Saved Difference
Model: mlogit mlogit
N: 200 200 0
Log-Lik Intercept Only: -204.097 -204.097 0.000
Log-Lik Full Model: -196.328 -196.024 -0.304
D: 392.656(196) 392.048(196) 0.608(0)
LR: 15.537(2) 16.145(2) 0.608(0)
Prob > LR: 0.000 0.000 .
McFadden's R2: 0.038 0.040 -0.001
McFadden's Adj R2: 0.018 0.020 -0.001
Maximum Likelihood R2: 0.075 0.078 -0.003
Cragg & Uhler's R2: 0.086 0.089 -0.003
Count R2: 0.545 0.525 0.020
Adj Count R2: 0.042 0.000 0.042
AIC: 2.003 2.000 0.003
AIC*n: 400.656 400.048 0.608
BIC: -645.814 -646.422 0.608
BIC': -4.941 -5.548 0.608
Difference of 0.608 in BIC' provides weak support for saved model.
Note: p-value for difference in LR is only valid if models are nested.
predict p1 p2 p3
(option p assumed; predicted probabilities)
list science prog p1 p2 p3 in 1/20, nolabel
+-------------------------------------------------+
| science prog p1 p2 p3 |
|-------------------------------------------------|
1. | 47 1 .2258013 .480244 .2939547 |
2. | 63 3 .2356738 .6384762 .1258499 |
3. | 58 1 .2371181 .5956004 .1672814 |
4. | 53 3 .2346923 .5465702 .2187374 |
5. | 53 2 .2346923 .5465702 .2187374 |
|-------------------------------------------------|
6. | 63 2 .2356738 .6384762 .1258499 |
7. | 53 1 .2346923 .5465702 .2187374 |
8. | 39 2 .203372 .3832462 .4133818 |
9. | 58 1 .2371181 .5956004 .1672814 |
10. | 50 2 .2311026 .5143352 .2545622 |
|-------------------------------------------------|
11. | 53 3 .2346923 .5465702 .2187374 |
12. | 63 2 .2356738 .6384762 .1258499 |
13. | 61 2 .2366667 .6220615 .1412718 |
14. | 55 2 .2361734 .5669116 .196915 |
15. | 31 2 .1711333 .2857407 .5431261 |
|-------------------------------------------------|
16. | 50 1 .2311026 .5143352 .2545622 |
17. | 50 2 .2311026 .5143352 .2545622 |
18. | 58 1 .2371181 .5956004 .1672814 |
19. | 55 2 .2361734 .5669116 .196915 |
20. | 53 1 .2346923 .5465702 .2187374 |
+-------------------------------------------------+
sort science
twoway connect p1 p2 p3 science, msym(i i i)
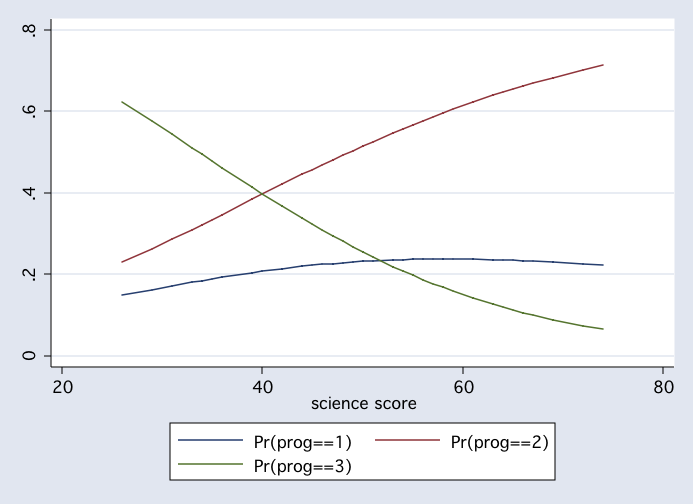 summarize p1 p2 p3
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
p1 | 200 .225 .0166541 .1483478 .2371181
p2 | 200 .525 .1044329 .2296548 .7127639
p3 | 200 .25 .119155 .0644656 .6219974
drop p1 p2 p3
summarize p1 p2 p3
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
p1 | 200 .225 .0166541 .1483478 .2371181
p2 | 200 .525 .1044329 .2296548 .7127639
p3 | 200 .25 .119155 .0644656 .6219974
drop p1 p2 p3
Here are some more of the Long & Freeze utilities.
prchange
mlogit: Changes in Predicted Probabilities for prog
science
Avg|Chg| general vocation academic
Min->Max .37168786 .07442269 -.55753179 .4831091
-+1/2 .00786675 .00113033 -.01180014 .01066977
-+sd/2 .07776304 .01132315 -.11664455 .10532141
MargEfct .00786688 .00113019 -.01180032 .01067013
general vocation academic
Pr(y|x) .23351446 .23203561 .53444993
science
x= 51.85
sd(x)= 9.90089
prtab science
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
----------------------
science |
score | Prediction
----------+-----------
26 | 0.1483
29 | 0.1621
31 | 0.1711
33 | 0.1799
34 | 0.1841
35 | 0.1882
36 | 0.1922
39 | 0.2034
40 | 0.2068
42 | 0.2131
44 | 0.2188
45 | 0.2213
46 | 0.2236
47 | 0.2258
48 | 0.2278
49 | 0.2295
50 | 0.2311
51 | 0.2325
53 | 0.2347
54 | 0.2355
55 | 0.2362
56 | 0.2367
57 | 0.2370
58 | 0.2371
59 | 0.2371
61 | 0.2367
63 | 0.2357
64 | 0.2350
65 | 0.2342
66 | 0.2333
67 | 0.2323
69 | 0.2299
72 | 0.2259
74 | 0.2228
----------------------
Predicted probability of outcome 3 (vocation)
----------------------
science |
score | Prediction
----------+-----------
26 | 0.6220
29 | 0.5752
31 | 0.5431
33 | 0.5106
34 | 0.4943
35 | 0.4780
36 | 0.4617
39 | 0.4134
40 | 0.3976
42 | 0.3666
44 | 0.3366
45 | 0.3220
46 | 0.3078
47 | 0.2940
48 | 0.2804
49 | 0.2673
50 | 0.2546
51 | 0.2422
53 | 0.2187
54 | 0.2076
55 | 0.1969
56 | 0.1866
57 | 0.1767
58 | 0.1673
59 | 0.1582
61 | 0.1413
63 | 0.1258
64 | 0.1187
65 | 0.1119
66 | 0.1054
67 | 0.0993
69 | 0.0879
72 | 0.0731
74 | 0.0645
----------------------
Predicted probability of outcome 2 (academic)
----------------------
science |
score | Prediction
----------+-----------
26 | 0.2297
29 | 0.2627
31 | 0.2857
33 | 0.3095
34 | 0.3216
35 | 0.3338
36 | 0.3461
39 | 0.3832
40 | 0.3956
42 | 0.4203
44 | 0.4446
45 | 0.4567
46 | 0.4685
47 | 0.4802
48 | 0.4918
49 | 0.5032
50 | 0.5143
51 | 0.5253
53 | 0.5466
54 | 0.5569
55 | 0.5669
56 | 0.5767
57 | 0.5863
58 | 0.5956
59 | 0.6047
61 | 0.6221
63 | 0.6385
64 | 0.6463
65 | 0.6539
66 | 0.6613
67 | 0.6685
69 | 0.6821
72 | 0.7011
74 | 0.7128
----------------------
science
x= 51.85
mlogtest, combine lrcomb
**** Wald tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 6.449 1 0.011
general-academic | 0.647 1 0.421
vocation-academic | 13.966 1 0.000
-------------------------------------------
**** LR tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 6.776 1 0.009
general-academic | 0.646 1 0.421
vocation-academic | 15.326 1 0.000
-------------------------------------------
tabstat science, by(prog)
Summary for variables: science
by categories of: prog (type of program)
prog | mean
---------+----------
general | 52.44444
academic | 53.8
vocation | 47.22
---------+----------
Total | 51.85
A Two Predictor Example
mlogit prog science honors, nolog
Multinomial logistic regression Number of obs = 200
LR chi2(4) = 25.11
Prob > chi2 = 0.0000
Log likelihood = -191.54213 Pseudo R2 = 0.0615
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
science | .0065831 .0204231 0.32 0.747 -.0334454 .0466117
honors | -1.260566 .4881122 -2.58 0.010 -2.217248 -.3038836
_cons | -.8718198 1.060829 -0.82 0.411 -2.951007 1.207367
-------------+----------------------------------------------------------------
vocation |
science | -.0530555 .0203973 -2.60 0.009 -.0930334 -.0130776
honors | -1.010628 .5178674 -1.95 0.051 -2.02563 .004373
_cons | 2.171415 .9955349 2.18 0.029 .2202025 4.122628
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
test science
( 1) [general]science = 0
( 2) [vocation]science = 0
chi2( 2) = 8.39
Prob > chi2 = 0.0151
test honors
( 1) [general]honors = 0
( 2) [vocation]honors = 0
chi2( 2) = 8.88
Prob > chi2 = 0.0118
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: science (sd= 9.9)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.05964 2.537 0.011 1.0615 1.8048
general -academic | 0.00658 0.322 0.747 1.0066 1.0673
vocation-general | -0.05964 -2.537 0.011 0.9421 0.5541
vocation-academic | -0.05306 -2.601 0.009 0.9483 0.5914
academic-general | -0.00658 -0.322 0.747 0.9934 0.9369
academic-vocation | 0.05306 2.601 0.009 1.0545 1.6910
----------------------------------------------------------------
Variable: honors (sd= .44)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | -0.24994 -0.390 0.696 0.7788 0.8953
general -academic | -1.26057 -2.583 0.010 0.2835 0.5725
vocation-general | 0.24994 0.390 0.696 1.2839 1.1169
vocation-academic | -1.01063 -1.952 0.051 0.3640 0.6395
academic-general | 1.26057 2.583 0.010 3.5274 1.7467
academic-vocation | 1.01063 1.952 0.051 2.7473 1.5638
----------------------------------------------------------------
fitstat, using(M1)
Measures of Fit for mlogit of prog
Current Saved Difference
Model: mlogit mlogit
N: 200 200 0
Log-Lik Intercept Only: -204.097 -204.097 0.000
Log-Lik Full Model: -191.542 -196.024 4.482
D: 383.084(194) 392.048(196) 8.964(2)
LR: 25.109(4) 16.145(2) 8.964(2)
Prob > LR: 0.000 0.000 0.011
McFadden's R2: 0.062 0.040 0.022
McFadden's Adj R2: 0.032 0.020 0.012
Maximum Likelihood R2: 0.118 0.078 0.040
Cragg & Uhler's R2: 0.136 0.089 0.046
Count R2: 0.540 0.525 0.015
Adj Count R2: 0.032 0.000 0.032
AIC: 1.975 2.000 -0.025
AIC*n: 395.084 400.048 -4.964
BIC: -644.789 -646.422 1.633
BIC': -3.916 -5.548 1.633
Difference of 1.633 in BIC' provides weak support for saved model.
Note: p-value for difference in LR is only valid if models are nested.
mlogtest, combine lrcomb
**** Wald tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 6.671 2 0.036
general-academic | 7.042 2 0.030
vocation-academic | 16.139 2 0.000
-------------------------------------------
**** LR tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 7.039 2 0.030
general-academic | 8.175 2 0.017
vocation-academic | 19.387 2 0.000
-------------------------------------------
prtab science honors
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
--------------------------
science | honors
score | 0 1
----------+---------------
26 | 0.1340 0.0724
29 | 0.1494 0.0785
31 | 0.1600 0.0825
33 | 0.1708 0.0866
34 | 0.1763 0.0886
35 | 0.1818 0.0906
36 | 0.1874 0.0926
39 | 0.2041 0.0985
40 | 0.2097 0.1004
42 | 0.2209 0.1042
44 | 0.2320 0.1079
45 | 0.2375 0.1097
46 | 0.2429 0.1116
47 | 0.2484 0.1133
48 | 0.2537 0.1151
49 | 0.2590 0.1168
50 | 0.2643 0.1186
51 | 0.2695 0.1203
53 | 0.2796 0.1236
54 | 0.2846 0.1252
55 | 0.2895 0.1268
56 | 0.2943 0.1284
57 | 0.2991 0.1300
58 | 0.3038 0.1315
59 | 0.3083 0.1330
61 | 0.3172 0.1360
63 | 0.3258 0.1389
64 | 0.3300 0.1403
65 | 0.3341 0.1417
66 | 0.3381 0.1431
67 | 0.3420 0.1445
69 | 0.3496 0.1472
72 | 0.3604 0.1511
74 | 0.3672 0.1536
--------------------------
Predicted probability of outcome 3 (vocation)
--------------------------
science | honors
score | 0 1
----------+---------------
26 | 0.5960 0.4133
29 | 0.5556 0.3747
31 | 0.5281 0.3499
33 | 0.5005 0.3257
34 | 0.4867 0.3140
35 | 0.4729 0.3025
36 | 0.4591 0.2913
39 | 0.4183 0.2590
40 | 0.4049 0.2488
42 | 0.3785 0.2292
44 | 0.3528 0.2107
45 | 0.3402 0.2019
46 | 0.3279 0.1933
47 | 0.3158 0.1850
48 | 0.3039 0.1770
49 | 0.2923 0.1693
50 | 0.2810 0.1619
51 | 0.2699 0.1547
53 | 0.2486 0.1411
54 | 0.2384 0.1346
55 | 0.2285 0.1285
56 | 0.2188 0.1225
57 | 0.2095 0.1169
58 | 0.2004 0.1114
59 | 0.1917 0.1062
61 | 0.1750 0.0963
63 | 0.1596 0.0873
64 | 0.1522 0.0831
65 | 0.1452 0.0791
66 | 0.1384 0.0752
67 | 0.1319 0.0716
69 | 0.1197 0.0647
72 | 0.1032 0.0555
74 | 0.0933 0.0501
--------------------------
Predicted probability of outcome 2 (academic)
--------------------------
science | honors
score | 0 1
----------+---------------
26 | 0.2700 0.5143
29 | 0.2951 0.5468
31 | 0.3119 0.5676
33 | 0.3287 0.5877
34 | 0.3370 0.5974
35 | 0.3453 0.6069
36 | 0.3535 0.6161
39 | 0.3776 0.6425
40 | 0.3854 0.6508
42 | 0.4006 0.6666
44 | 0.4152 0.6814
45 | 0.4223 0.6884
46 | 0.4292 0.6951
47 | 0.4358 0.7016
48 | 0.4423 0.7079
49 | 0.4486 0.7138
50 | 0.4547 0.7196
51 | 0.4606 0.7251
53 | 0.4717 0.7354
54 | 0.4770 0.7401
55 | 0.4820 0.7447
56 | 0.4868 0.7491
57 | 0.4914 0.7532
58 | 0.4958 0.7571
59 | 0.5000 0.7608
61 | 0.5077 0.7677
63 | 0.5146 0.7738
64 | 0.5178 0.7766
65 | 0.5207 0.7792
66 | 0.5235 0.7817
67 | 0.5261 0.7840
69 | 0.5307 0.7881
72 | 0.5365 0.7934
74 | 0.5395 0.7962
--------------------------
science honors
x= 51.85 .265
Categorical Predictor Example
tabulate ses, gen(ses)
ses | Freq. Percent Cum.
------------+-----------------------------------
low | 47 23.50 23.50
middle | 95 47.50 71.00
high | 58 29.00 100.00
------------+-----------------------------------
Total | 200 100.00
mlogit prog ses1 ses2, nolog
Multinomial logistic regression Number of obs = 200
LR chi2(4) = 16.78
Prob > chi2 = 0.0021
Log likelihood = -195.70519 Pseudo R2 = 0.0411
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
ses1 | 1.368595 .5000526 2.74 0.006 .3885097 2.34868
ses2 | .7519877 .4556845 1.65 0.099 -.1411374 1.645113
_cons | -1.540445 .367316 -4.19 0.000 -2.260371 -.8205189
-------------+----------------------------------------------------------------
vocation |
ses1 | 1.332227 .5501167 2.42 0.015 .2540182 2.410436
ses2 | 1.441557 .470796 3.06 0.002 .5188139 2.3643
_cons | -1.791759 .4082444 -4.39 0.000 -2.591904 -.9916151
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
test ses1 ses2
( 1) [general]ses1 = 0
( 2) [vocation]ses1 = 0
( 3) [general]ses2 = 0
( 4) [vocation]ses2 = 0
chi2( 4) = 15.67
Prob > chi2 = 0.0035
Final Model: Three Predictors
mlogit prog science honors ses1 ses2, nolog
Multinomial logistic regression Number of obs = 200
LR chi2(8) = 37.66
Prob > chi2 = 0.0000
Log likelihood = -185.26706 Pseudo R2 = 0.0923
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
science | .0196812 .0213451 0.92 0.357 -.0221545 .0615168
honors | -1.254872 .5053887 -2.48 0.013 -2.245416 -.2643289
ses1 | 1.323819 .5279468 2.51 0.012 .2890618 2.358575
ses2 | .5173172 .4725885 1.09 0.274 -.4089392 1.443574
_cons | -2.146701 1.201467 -1.79 0.074 -4.501532 .2081308
-------------+----------------------------------------------------------------
vocation |
science | -.052548 .0215222 -2.44 0.015 -.0947306 -.0103653
honors | -.8064186 .5309991 -1.52 0.129 -1.847158 .2343204
ses1 | .8638298 .5844485 1.48 0.139 -.2816682 2.009328
ses2 | 1.167853 .4932099 2.37 0.018 .2011791 2.134526
_cons | 1.280312 1.133052 1.13 0.258 -.9404289 3.501053
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
test science
( 1) [general]science = 0
( 2) [vocation]science = 0
chi2( 2) = 9.28
Prob > chi2 = 0.0097
test honors
( 1) [general]honors = 0
( 2) [vocation]honors = 0
chi2( 2) = 7.25
Prob > chi2 = 0.0267
test ses1 ses2
( 1) [general]ses1 = 0
( 2) [vocation]ses1 = 0
( 3) [general]ses2 = 0
( 4) [vocation]ses2 = 0
chi2( 4) = 9.88
Prob > chi2 = 0.0424
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: science (sd= 9.9)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.07223 2.905 0.004 1.0749 2.0445
general -academic | 0.01968 0.922 0.357 1.0199 1.2151
vocation-general | -0.07223 -2.905 0.004 0.9303 0.4891
vocation-academic | -0.05255 -2.442 0.015 0.9488 0.5944
academic-general | -0.01968 -0.922 0.357 0.9805 0.8229
academic-vocation | 0.05255 2.442 0.015 1.0540 1.6825
----------------------------------------------------------------
Variable: honors (sd= .44)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | -0.44845 -0.684 0.494 0.6386 0.8200
general -academic | -1.25487 -2.483 0.013 0.2851 0.5740
vocation-general | 0.44845 0.684 0.494 1.5659 1.2195
vocation-academic | -0.80642 -1.519 0.129 0.4465 0.6999
academic-general | 1.25487 2.483 0.013 3.5074 1.7423
academic-vocation | 0.80642 1.519 0.129 2.2399 1.4287
----------------------------------------------------------------
Variable: ses1 (sd= .43)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.45999 0.688 0.491 1.5841 1.2159
general -academic | 1.32382 2.507 0.012 3.7577 1.7554
vocation-general | -0.45999 -0.688 0.491 0.6313 0.8224
vocation-academic | 0.86383 1.478 0.139 2.3722 1.4437
academic-general | -1.32382 -2.507 0.012 0.2661 0.5697
academic-vocation | -0.86383 -1.478 0.139 0.4215 0.6927
----------------------------------------------------------------
Variable: ses2 (sd= .5)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | -0.65054 -1.083 0.279 0.5218 0.7220
general -academic | 0.51732 1.095 0.274 1.6775 1.2956
vocation-general | 0.65054 1.083 0.279 1.9166 1.3850
vocation-academic | 1.16785 2.368 0.018 3.2151 1.7944
academic-general | -0.51732 -1.095 0.274 0.5961 0.7718
academic-vocation | -1.16785 -2.368 0.018 0.3110 0.5573
----------------------------------------------------------------
fitstat, using(M1)
Measures of Fit for mlogit of prog
Current Saved Difference
Model: mlogit mlogit
N: 200 200 0
Log-Lik Intercept Only: -204.097 -204.097 0.000
Log-Lik Full Model: -185.267 -196.024 10.757
D: 370.534(190) 392.048(196) 21.514(6)
LR: 37.659(8) 16.145(2) 21.514(6)
Prob > LR: 0.000 0.000 0.001
McFadden's R2: 0.092 0.040 0.053
McFadden's Adj R2: 0.043 0.020 0.023
Maximum Likelihood R2: 0.172 0.078 0.094
Cragg & Uhler's R2: 0.197 0.089 0.108
Count R2: 0.575 0.525 0.050
Adj Count R2: 0.105 0.000 0.105
AIC: 1.953 2.000 -0.048
AIC*n: 390.534 400.048 -9.514
BIC: -636.146 -646.422 10.276
BIC': 4.727 -5.548 10.276
Difference of 10.276 in BIC' provides very strong support for saved model.
Note: p-value for difference in LR is only valid if models are nested.
prchange, x(honors=1 ses1=0 ses2=1)
mlogit: Changes in Predicted Probabilities for prog
science
Avg|Chg| general vocation academic
Min->Max .31191427 .13955039 -.46787138 .32832104
-+1/2 .0064501 .00306802 -.00967517 .00660712
-+sd/2 .06380373 .03033344 -.0957056 .06537217
MargEfct .00645018 .00306807 -.00967527 .0066072
honors
Avg|Chg| general vocation academic
0->1 .15676552 -.132423 -.1027253 .23514825
ses1
Avg|Chg| general vocation academic
0->1 .1669159 .14041305 .10996082 -.25037384
ses2
Avg|Chg| general vocation academic
0->1 .11027237 .0266413 .13876726 -.16540855
general vocation academic
Pr(y|x) .10382493 .22670016 .6694749
science honors ses1 ses2
x= 51.85 1 0 1
sd(x)= 9.90089 .442441 .425063 .500628
prtab science honors, x(ses1=0 ses2=1)
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
--------------------------
science | honors
score | 0 1
----------+---------------
26 | 0.0765 0.0387
29 | 0.0897 0.0445
31 | 0.0994 0.0486
33 | 0.1098 0.0530
34 | 0.1153 0.0553
35 | 0.1209 0.0576
36 | 0.1267 0.0600
39 | 0.1450 0.0674
40 | 0.1514 0.0700
42 | 0.1647 0.0753
44 | 0.1784 0.0808
45 | 0.1855 0.0836
46 | 0.1927 0.0865
47 | 0.1999 0.0893
48 | 0.2073 0.0923
49 | 0.2147 0.0952
50 | 0.2222 0.0982
51 | 0.2298 0.1012
53 | 0.2451 0.1074
54 | 0.2528 0.1105
55 | 0.2605 0.1136
56 | 0.2683 0.1168
57 | 0.2761 0.1200
58 | 0.2838 0.1233
59 | 0.2916 0.1265
61 | 0.3072 0.1331
63 | 0.3226 0.1398
64 | 0.3303 0.1432
65 | 0.3380 0.1466
66 | 0.3456 0.1500
67 | 0.3532 0.1535
69 | 0.3682 0.1604
72 | 0.3903 0.1710
74 | 0.4048 0.1782
--------------------------
Predicted probability of outcome 3 (vocation)
--------------------------
science | honors
score | 0 1
----------+---------------
26 | 0.6898 0.5465
29 | 0.6517 0.5059
31 | 0.6251 0.4787
33 | 0.5976 0.4517
34 | 0.5836 0.4382
35 | 0.5694 0.4248
36 | 0.5551 0.4116
39 | 0.5116 0.3725
40 | 0.4970 0.3598
42 | 0.4678 0.3350
44 | 0.4387 0.3111
45 | 0.4242 0.2994
46 | 0.4099 0.2880
47 | 0.3957 0.2769
48 | 0.3817 0.2660
49 | 0.3678 0.2554
50 | 0.3541 0.2451
51 | 0.3407 0.2350
53 | 0.3145 0.2158
54 | 0.3018 0.2066
55 | 0.2893 0.1976
56 | 0.2772 0.1890
57 | 0.2654 0.1807
58 | 0.2538 0.1726
59 | 0.2426 0.1648
61 | 0.2212 0.1501
63 | 0.2011 0.1364
64 | 0.1915 0.1300
65 | 0.1823 0.1238
66 | 0.1734 0.1179
67 | 0.1649 0.1122
69 | 0.1488 0.1015
72 | 0.1270 0.0871
74 | 0.1140 0.0786
--------------------------
Predicted probability of outcome 2 (academic)
--------------------------
science | honors
score | 0 1
----------+---------------
26 | 0.2338 0.4149
29 | 0.2586 0.4496
31 | 0.2755 0.4727
33 | 0.2926 0.4953
34 | 0.3012 0.5065
35 | 0.3097 0.5176
36 | 0.3182 0.5284
39 | 0.3434 0.5600
40 | 0.3516 0.5701
42 | 0.3675 0.5896
44 | 0.3829 0.6081
45 | 0.3903 0.6170
46 | 0.3974 0.6255
47 | 0.4044 0.6338
48 | 0.4111 0.6417
49 | 0.4175 0.6494
50 | 0.4237 0.6567
51 | 0.4295 0.6637
53 | 0.4405 0.6769
54 | 0.4455 0.6830
55 | 0.4501 0.6887
56 | 0.4545 0.6942
57 | 0.4586 0.6993
58 | 0.4623 0.7042
59 | 0.4658 0.7087
61 | 0.4716 0.7168
63 | 0.4763 0.7238
64 | 0.4781 0.7268
65 | 0.4797 0.7296
66 | 0.4810 0.7321
67 | 0.4819 0.7344
69 | 0.4830 0.7381
72 | 0.4827 0.7418
74 | 0.4812 0.7432
--------------------------
science honors ses1 ses2
x= 51.85 .265 0 1
