You can view movies of this seminar via the links below.
The purpose of this seminar is to give users an introduction to analyzing multinomial logistic models using Stata. In addition to the built-in Stata commands we will be demonstrating the use of a number on user-written ado’s, in particular, listcoef, fitstat, prchange, prtab, etc. To find out more about these programs or to download them type search followed by the program name in the Stata command window (example: search listcoef). These add-on programs ease the running and interpretation of ordinal logistic models.
Binary Response Variable Example
Let’s begin with an example using a binary response variable. We will see that the results of an multinomial logistic model are exactly the same as for a traditional logistic model.
use https://stats.idre.ucla.edu/stat/stata/seminars/stata_BeyondBinaryLogistic/honors, clear
logit honors female
Iteration 0: log likelihood = -115.64441
Iteration 1: log likelihood = -113.68907
Iteration 2: log likelihood = -113.67691
Iteration 3: log likelihood = -113.6769
Logit estimates Number of obs = 200
LR chi2(1) = 3.94
Prob > chi2 = 0.0473
Log likelihood = -113.6769 Pseudo R2 = 0.0170
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | .6513707 .3336752 1.95 0.051 -.0026207 1.305362
_cons | -1.400088 .2631619 -5.32 0.000 -1.915876 -.8842998
------------------------------------------------------------------------------
mlogit honors female
Iteration 0: log likelihood = -115.64441
Iteration 1: log likelihood = -113.68907
Iteration 2: log likelihood = -113.67691
Iteration 3: log likelihood = -113.6769
Multinomial logistic regression Number of obs = 200
LR chi2(1) = 3.94
Prob > chi2 = 0.0473
Log likelihood = -113.6769 Pseudo R2 = 0.0170
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1 |
female | .6513707 .3336752 1.95 0.051 -.0026207 1.305362
_cons | -1.400088 .2631619 -5.32 0.000 -1.915876 -.8842998
------------------------------------------------------------------------------
(Outcome honors==0 is the comparison group)
predict p0 p1
(option p assumed; predicted probabilities)
list female honors p0 p1 in 1/20, nolabel
+---------------------------------------+
| female honors p0 p1 |
|---------------------------------------|
1. | 1 0 .6788991 .3211009 |
2. | 0 0 .8021978 .1978022 |
3. | 0 0 .8021978 .1978022 |
4. | 1 1 .6788991 .3211009 |
5. | 1 1 .6788991 .3211009 |
|---------------------------------------|
6. | 0 0 .8021978 .1978022 |
7. | 1 0 .6788991 .3211009 |
8. | 1 0 .6788991 .3211009 |
9. | 1 0 .6788991 .3211009 |
10. | 1 0 .6788991 .3211009 |
|---------------------------------------|
11. | 1 1 .6788991 .3211009 |
12. | 0 0 .8021978 .1978022 |
13. | 0 0 .8021978 .1978022 |
14. | 1 0 .6788991 .3211009 |
15. | 1 0 .6788991 .3211009 |
|---------------------------------------|
16. | 1 0 .6788991 .3211009 |
17. | 0 0 .8021978 .1978022 |
18. | 1 0 .6788991 .3211009 |
19. | 1 1 .6788991 .3211009 |
20. | 1 0 .6788991 .3211009 |
+---------------------------------------+
3-Category Response Variable Example
use https://stats.idre.ucla.edu/stat/stata/seminars/stata_BeyondBinaryLogistic/hsb2, clear
(highschool and beyond (200 cases))
codebook prog
prog type of program
----------------------------------------------------------------------------------------------------------
type: numeric (float)
label: sel
range: [1,3] units: 1
unique values: 3 missing .: 0/200
tabulation: Freq. Numeric Label
45 1 general
105 2 academic
50 3 vocation
mlogit prog female
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -204.07028
Iteration 2: log likelihood = -204.07028
Multinomial logistic regression Number of obs = 200
LR chi2(2) = 0.05
Prob > chi2 = 0.9739
Log likelihood = -204.07028 Pseudo R2 = 0.0001
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
female | -.076764 .3574964 -0.21 0.830 -.7774441 .6239161
_cons | -.8056252 .2624798 -3.07 0.002 -1.320076 -.2911742
-------------+----------------------------------------------------------------
vocation |
female | -.0499528 .345012 -0.14 0.885 -.7261638 .6262583
_cons | -.7146534 .2544698 -2.81 0.005 -1.213405 -.2159018
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
mlogit, rrr /* relative risk ratios */
Multinomial logistic regression Number of obs = 200
LR chi2(2) = 0.05
Prob > chi2 = 0.9739
Log likelihood = -204.07028 Pseudo R2 = 0.0001
------------------------------------------------------------------------------
prog | RRR Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
female | .9261084 .3310804 -0.21 0.830 .4595791 1.866222
-------------+----------------------------------------------------------------
vocation |
female | .9512744 .3282011 -0.14 0.885 .4837612 1.870598
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
Next, we look at some of the Long & Freese utilities.
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: female (sd= .5)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | -0.02681 -0.065 0.948 0.9735 0.9867
general -academic | -0.07676 -0.215 0.830 0.9261 0.9624
vocation-general | 0.02681 0.065 0.948 1.0272 1.0135
vocation-academic | -0.04995 -0.145 0.885 0.9513 0.9754
academic-general | 0.07676 0.215 0.830 1.0798 1.0391
academic-vocation | 0.04995 0.145 0.885 1.0512 1.0253
----------------------------------------------------------------
listcoef, percent
mlogit (N=200): Percentage Change in the Odds of prog
Variable: female (sd= .5)
Odds comparing|
Group 1 vs Group 2| b z P>|z| % %StdX
------------------+---------------------------------------------
general -vocation | -0.02681 -0.065 0.948 -2.6 -1.3
general -academic | -0.07676 -0.215 0.830 -7.4 -3.8
vocation-general | 0.02681 0.065 0.948 2.7 1.3
vocation-academic | -0.04995 -0.145 0.885 -4.9 -2.5
academic-general | 0.07676 0.215 0.830 8.0 3.9
academic-vocation | 0.04995 0.145 0.885 5.1 2.5
----------------------------------------------------------------
fitstat
Measures of Fit for mlogit of prog
Log-Lik Intercept Only: -204.097 Log-Lik Full Model: -204.070
D(196): 408.141 LR(2): 0.053
Prob > LR: 0.974
McFadden's R2: 0.000 McFadden's Adj R2: -0.019
Maximum Likelihood R2: 0.000 Cragg & Uhler's R2: 0.000
Count R2: 0.525 Adj Count R2: 0.000
AIC: 2.081 AIC*n: 416.141
BIC: -630.330 BIC': 10.544
prchange
mlogit: Changes in Predicted Probabilities for prog
female
Avg|Chg| general vocation academic
0->1 .01041771 -.01058574 -.00504084 .01562655
general vocation academic
Pr(y|x) .22496811 .25002041 .52501148
female
x= .545
sd(x)= .49922
prtab female
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
----------------------
female | Prediction
----------+-----------
male | 0.2308
female | 0.2202
----------------------
Predicted probability of outcome 3 (vocation)
----------------------
female | Prediction
----------+-----------
male | 0.2527
female | 0.2477
----------------------
Predicted probability of outcome 2 (academic)
----------------------
female | Prediction
----------+-----------
male | 0.5165
female | 0.5321
----------------------
female
x= .545
predict p1 p2 p3
(option p assumed; predicted probabilities)
list female prog p1 p2 p3 in 1/20, nolabel
+------------------------------------------------+
| female prog p1 p2 p3 |
|------------------------------------------------|
1. | 0 1 .2307692 .5164835 .2527473 |
2. | 1 3 .2201835 .5321101 .2477064 |
3. | 0 1 .2307692 .5164835 .2527473 |
4. | 0 3 .2307692 .5164835 .2527473 |
5. | 0 2 .2307692 .5164835 .2527473 |
|------------------------------------------------|
6. | 0 2 .2307692 .5164835 .2527473 |
7. | 0 1 .2307692 .5164835 .2527473 |
8. | 0 2 .2307692 .5164835 .2527473 |
9. | 0 1 .2307692 .5164835 .2527473 |
10. | 0 2 .2307692 .5164835 .2527473 |
|------------------------------------------------|
11. | 0 3 .2307692 .5164835 .2527473 |
12. | 0 2 .2307692 .5164835 .2527473 |
13. | 0 2 .2307692 .5164835 .2527473 |
14. | 0 2 .2307692 .5164835 .2527473 |
15. | 0 2 .2307692 .5164835 .2527473 |
|------------------------------------------------|
16. | 0 1 .2307692 .5164835 .2527473 |
17. | 0 2 .2307692 .5164835 .2527473 |
18. | 0 1 .2307692 .5164835 .2527473 |
19. | 0 2 .2307692 .5164835 .2527473 |
20. | 0 1 .2307692 .5164835 .2527473 |
+------------------------------------------------+
drop p1 p2 p3
An Example Using a Continuous Predictor
mlogit prog read
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -185.28771
Iteration 2: log likelihood = -184.59416
Iteration 3: log likelihood = -184.58662
Iteration 4: log likelihood = -184.58661
Multinomial logistic regression Number of obs = 200
LR chi2(2) = 39.02
Prob > chi2 = 0.0000
Log likelihood = -184.58661 Pseudo R2 = 0.0956
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
read | -.0703559 .0200906 -3.50 0.000 -.1097328 -.0309791
_cons | 2.874114 1.054187 2.73 0.006 .8079463 4.940282
-------------+----------------------------------------------------------------
vocation |
read | -.1164723 .0223442 -5.21 0.000 -.1602662 -.0726784
_cons | 5.189645 1.116495 4.65 0.000 3.001355 7.377934
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: read (sd= 10)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.04612 1.924 0.054 1.0472 1.6045
general -academic | -0.07036 -3.502 0.000 0.9321 0.4861
vocation-general | -0.04612 -1.924 0.054 0.9549 0.6232
vocation-academic | -0.11647 -5.213 0.000 0.8901 0.3030
academic-general | 0.07036 3.502 0.000 1.0729 2.0572
academic-vocation | 0.11647 5.213 0.000 1.1235 3.3009
----------------------------------------------------------------
fitstat
Measures of Fit for mlogit of prog
Log-Lik Intercept Only: -204.097 Log-Lik Full Model: -184.587
D(196): 369.173 LR(2): 39.020
Prob > LR: 0.000
McFadden's R2: 0.096 McFadden's Adj R2: 0.076
Maximum Likelihood R2: 0.177 Cragg & Uhler's R2: 0.204
Count R2: 0.585 Adj Count R2: 0.126
AIC: 1.886 AIC*n: 377.173
BIC: -669.297 BIC': -28.423
predict p1 p2 p3
(option p assumed; predicted probabilities)
list read prog p1 p2 p3 in 1/20, nolabel
+----------------------------------------------+
| read prog p1 p2 p3 |
|----------------------------------------------|
1. | 57 1 .2063555 .6427623 .1508822 |
2. | 68 3 .1220411 .8242286 .0537303 |
3. | 44 1 .2793571 .3486395 .3720033 |
4. | 63 3 .1585986 .7534682 .0879332 |
5. | 47 2 .2702068 .4164652 .3133279 |
|----------------------------------------------|
6. | 44 2 .2793571 .3486395 .3720033 |
7. | 50 1 .2555427 .4864202 .2580371 |
8. | 34 2 .2681388 .1655863 .5662749 |
9. | 63 1 .1585986 .7534682 .0879332 |
10. | 57 2 .2063555 .6427623 .1508822 |
|----------------------------------------------|
11. | 60 3 .182365 .7015224 .1161126 |
12. | 57 2 .2063555 .6427623 .1508822 |
13. | 73 2 .091319 .8767558 .0319252 |
14. | 54 2 .229263 .5782328 .1925042 |
15. | 45 2 .2769624 .3708454 .3521922 |
|----------------------------------------------|
16. | 42 1 .2821275 .3058806 .4119919 |
17. | 47 2 .2702068 .4164652 .3133279 |
18. | 57 1 .2063555 .6427623 .1508822 |
19. | 68 2 .1220411 .8242286 .0537303 |
20. | 55 1 .2218377 .6002877 .1778745 |
+----------------------------------------------+
sort read
scatter p1 p2 p3 read, connect(l l l) msym(i i i)
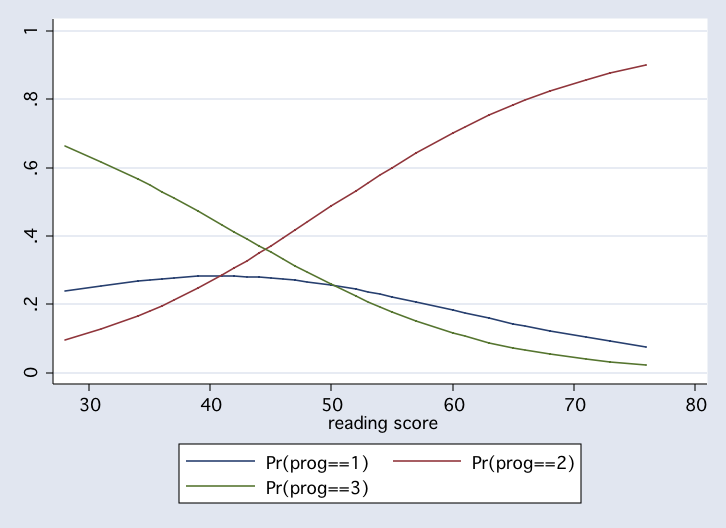summarize p1 p2 p3
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
p1 | 200 .225 .0582549 .0759783 .2825051
p2 | 200 .525 .2033302 .0966327 .9008916
p3 | 200 .25 .1509281 .0231301 .6647014
list read p1 p2 p3 if p1>p2
+---------------------------------------+
| read p1 p2 p3 |
|---------------------------------------|
1. | 28 .2386659 .0966327 .6647014 |
2. | 31 .2547603 .1273887 .617851 |
3. | 34 .2681388 .1655863 .5662749 |
4. | 34 .2681388 .1655863 .5662749 |
5. | 34 .2681388 .1655863 .5662749 |
|---------------------------------------|
6. | 34 .2681388 .1655863 .5662749 |
7. | 34 .2681388 .1655863 .5662749 |
8. | 34 .2681388 .1655863 .5662749 |
9. | 35 .2717949 .1800783 .5481268 |
10. | 36 .2749785 .1954673 .5295542 |
|---------------------------------------|
11. | 36 .2749785 .1954673 .5295542 |
12. | 36 .2749785 .1954673 .5295542 |
13. | 37 .2776492 .2117517 .5105991 |
14. | 37 .2776492 .2117517 .5105991 |
15. | 39 .2813043 .2469546 .4717411 |
|---------------------------------------|
16. | 39 .2813043 .2469546 .4717411 |
17. | 39 .2813043 .2469546 .4717411 |
18. | 39 .2813043 .2469546 .4717411 |
19. | 39 .2813043 .2469546 .4717411 |
20. | 39 .2813043 .2469546 .4717411 |
|---------------------------------------|
21. | 39 .2813043 .2469546 .4717411 |
22. | 39 .2813043 .2469546 .4717411 |
+---------------------------------------+
list read prog p1 p2 p3 if p1>p2 & p1>p3
drop p1 p2 p3
Here are some more of the Long & Freeze utilities.
prchange
mlogit: Changes in Predicted Probabilities for prog
read
Avg|Chg| general vocation academic
Min->Max .53617262 -.16268767 -.64157127 .80425891
-+1/2 .01529801 -.00669396 -.01625305 .02294701
-+sd/2 .15414272 -.06625439 -.1649597 .23121408
MargEfct .0153006 -.00669624 -.01625465 .02295089
general vocation academic
Pr(y|x) .24166824 .22017884 .53815293
read
x= 52.23
sd(x)= 10.2529
prtab read
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
----------------------
reading |
score | Prediction
----------+-----------
28 | 0.2387
31 | 0.2548
34 | 0.2681
35 | 0.2718
36 | 0.2750
37 | 0.2776
39 | 0.2813
41 | 0.2825
42 | 0.2821
43 | 0.2811
44 | 0.2794
45 | 0.2770
46 | 0.2739
47 | 0.2702
48 | 0.2659
50 | 0.2555
52 | 0.2432
53 | 0.2364
54 | 0.2293
55 | 0.2218
57 | 0.2064
60 | 0.1824
61 | 0.1744
63 | 0.1586
65 | 0.1434
66 | 0.1361
68 | 0.1220
71 | 0.1028
73 | 0.0913
76 | 0.0760
----------------------
Predicted probability of outcome 3 (vocation)
----------------------
reading |
score | Prediction
----------+-----------
28 | 0.6647
31 | 0.6179
34 | 0.5663
35 | 0.5481
36 | 0.5296
37 | 0.5106
39 | 0.4717
41 | 0.4320
42 | 0.4120
43 | 0.3920
44 | 0.3720
45 | 0.3522
46 | 0.3326
47 | 0.3133
48 | 0.2944
50 | 0.2580
52 | 0.2239
53 | 0.2079
54 | 0.1925
55 | 0.1779
57 | 0.1509
60 | 0.1161
61 | 0.1060
63 | 0.0879
65 | 0.0725
66 | 0.0657
68 | 0.0537
71 | 0.0394
73 | 0.0319
76 | 0.0231
----------------------
Predicted probability of outcome 2 (academic)
----------------------
reading |
score | Prediction
----------+-----------
28 | 0.0966
31 | 0.1274
34 | 0.1656
35 | 0.1801
36 | 0.1955
37 | 0.2118
39 | 0.2470
41 | 0.2855
42 | 0.3059
43 | 0.3270
44 | 0.3486
45 | 0.3708
46 | 0.3935
47 | 0.4165
48 | 0.4397
50 | 0.4864
52 | 0.5329
53 | 0.5557
54 | 0.5782
55 | 0.6003
57 | 0.6428
60 | 0.7015
61 | 0.7196
63 | 0.7535
65 | 0.7841
66 | 0.7983
68 | 0.8242
71 | 0.8577
73 | 0.8768
76 | 0.9009
----------------------
read
x= 52.23
mlogtest, combine lrcomb
**** Wald tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 3.703 1 0.054
general-academic | 12.264 1 0.000
vocation-academic | 27.172 1 0.000
-------------------------------------------
**** LR tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 3.838 1 0.050
general-academic | 13.660 1 0.000
vocation-academic | 35.553 1 0.000
-------------------------------------------
A Two Predictor Example
mlogit prog read female
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -185.12283
Iteration 2: log likelihood = -184.41244
Iteration 3: log likelihood = -184.40469
Iteration 4: log likelihood = -184.40469
Multinomial logistic regression Number of obs = 200
LR chi2(4) = 39.38
Prob > chi2 = 0.0000
Log likelihood = -184.40469 Pseudo R2 = 0.0965
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
read | -.0712123 .0202062 -3.52 0.000 -.1108158 -.0316089
female | -.1834744 .3726879 -0.49 0.623 -.9139293 .5469805
_cons | 3.019251 1.096285 2.75 0.006 .8705724 5.16793
-------------+----------------------------------------------------------------
vocation |
read | -.1172833 .0224395 -5.23 0.000 -.161264 -.0733026
female | -.193847 .3800557 -0.51 0.610 -.9387425 .5510486
_cons | 5.33822 1.156404 4.62 0.000 3.07171 7.60473
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: read (sd= 10)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.04607 1.922 0.055 1.0471 1.6038
general -academic | -0.07121 -3.524 0.000 0.9313 0.4818
vocation-general | -0.04607 -1.922 0.055 0.9550 0.6235
vocation-academic | -0.11728 -5.227 0.000 0.8893 0.3004
academic-general | 0.07121 3.524 0.000 1.0738 2.0754
academic-vocation | 0.11728 5.227 0.000 1.1244 3.3284
----------------------------------------------------------------
Variable: female (sd= .5)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.01037 0.025 0.980 1.0104 1.0052
general -academic | -0.18347 -0.492 0.623 0.8324 0.9125
vocation-general | -0.01037 -0.025 0.980 0.9897 0.9948
vocation-academic | -0.19385 -0.510 0.610 0.8238 0.9078
academic-general | 0.18347 0.492 0.623 1.2014 1.0959
academic-vocation | 0.19385 0.510 0.610 1.2139 1.1016
----------------------------------------------------------------
fitstat
Measures of Fit for mlogit of prog
Log-Lik Intercept Only: -204.097 Log-Lik Full Model: -184.405
D(194): 368.809 LR(4): 39.384
Prob > LR: 0.000
McFadden's R2: 0.096 McFadden's Adj R2: 0.067
Maximum Likelihood R2: 0.179 Cragg & Uhler's R2: 0.205
Count R2: 0.590 Adj Count R2: 0.137
AIC: 1.904 AIC*n: 380.809
BIC: -659.064 BIC': -18.191
mlogtest, combine lrcomb
**** Wald tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 3.697 2 0.157
general-academic | 12.455 2 0.002
vocation-academic | 27.333 2 0.000
-------------------------------------------
**** LR tests for combining outcome categories
Ho: All coefficients except intercepts associated with given pair
of outcomes are 0 (i.e., categories can be collapsed).
Categories tested | chi2 df P>chi2
------------------+------------------------
general-vocation | 3.833 2 0.147
general-academic | 13.916 2 0.001
vocation-academic | 35.841 2 0.000
-------------------------------------------
prtab read female
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.2406 0.2381
31 | 0.2577 0.2535
34 | 0.2723 0.2659
35 | 0.2764 0.2692
36 | 0.2801 0.2719
37 | 0.2833 0.2742
39 | 0.2881 0.2769
41 | 0.2905 0.2771
42 | 0.2907 0.2762
43 | 0.2902 0.2746
44 | 0.2890 0.2724
45 | 0.2872 0.2694
46 | 0.2846 0.2659
47 | 0.2814 0.2617
48 | 0.2775 0.2569
50 | 0.2678 0.2457
52 | 0.2559 0.2327
53 | 0.2492 0.2257
54 | 0.2422 0.2183
55 | 0.2347 0.2107
57 | 0.2191 0.1951
60 | 0.1944 0.1712
61 | 0.1861 0.1633
63 | 0.1696 0.1479
65 | 0.1536 0.1331
66 | 0.1459 0.1261
68 | 0.1310 0.1127
71 | 0.1105 0.0944
73 | 0.0981 0.0836
76 | 0.0816 0.0692
--------------------------
Predicted probability of outcome 3 (vocation)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.6731 0.6593
31 | 0.6279 0.6113
34 | 0.5780 0.5585
35 | 0.5603 0.5399
36 | 0.5422 0.5209
37 | 0.5237 0.5016
39 | 0.4857 0.4619
41 | 0.4466 0.4216
42 | 0.4268 0.4013
43 | 0.4069 0.3810
44 | 0.3870 0.3609
45 | 0.3672 0.3410
46 | 0.3475 0.3213
47 | 0.3281 0.3020
48 | 0.3090 0.2831
50 | 0.2720 0.2470
52 | 0.2370 0.2133
53 | 0.2204 0.1975
54 | 0.2045 0.1825
55 | 0.1893 0.1682
57 | 0.1612 0.1420
60 | 0.1246 0.1085
61 | 0.1139 0.0989
63 | 0.0947 0.0817
65 | 0.0782 0.0670
66 | 0.0709 0.0606
68 | 0.0580 0.0494
71 | 0.0426 0.0361
73 | 0.0345 0.0291
76 | 0.0250 0.0210
--------------------------
Predicted probability of outcome 2 (academic)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.0863 0.1026
31 | 0.1144 0.1352
34 | 0.1497 0.1756
35 | 0.1632 0.1909
36 | 0.1776 0.2071
37 | 0.1929 0.2243
39 | 0.2262 0.2612
41 | 0.2630 0.3013
42 | 0.2826 0.3225
43 | 0.3029 0.3444
44 | 0.3240 0.3667
45 | 0.3456 0.3896
46 | 0.3678 0.4128
47 | 0.3905 0.4363
48 | 0.4135 0.4600
50 | 0.4602 0.5073
52 | 0.5071 0.5540
53 | 0.5303 0.5768
54 | 0.5533 0.5992
55 | 0.5759 0.6211
57 | 0.6198 0.6629
60 | 0.6810 0.7203
61 | 0.7000 0.7378
63 | 0.7357 0.7705
65 | 0.7682 0.7998
66 | 0.7833 0.8133
68 | 0.8110 0.8379
71 | 0.8469 0.8695
73 | 0.8673 0.8873
76 | 0.8934 0.9098
--------------------------
read female
x= 52.23 .545
Categorical Predictor Example
tabulate ses, gen(ses)
ses | Freq. Percent Cum.
------------+-----------------------------------
low | 47 23.50 23.50
middle | 95 47.50 71.00
high | 58 29.00 100.00
------------+-----------------------------------
Total | 200 100.00
mlogit prog ses1 ses2
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -195.82855
Iteration 2: log likelihood = -195.70541
Iteration 3: log likelihood = -195.70519
Multinomial logistic regression Number of obs = 200
LR chi2(4) = 16.78
Prob > chi2 = 0.0021
Log likelihood = -195.70519 Pseudo R2 = 0.0411
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
ses1 | 1.368595 .5000526 2.74 0.006 .3885097 2.34868
ses2 | .7519877 .4556845 1.65 0.099 -.1411374 1.645113
_cons | -1.540445 .367316 -4.19 0.000 -2.260371 -.8205189
-------------+----------------------------------------------------------------
vocation |
ses1 | 1.332227 .5501167 2.42 0.015 .2540182 2.410436
ses2 | 1.441557 .470796 3.06 0.002 .5188139 2.3643
_cons | -1.791759 .4082444 -4.39 0.000 -2.591904 -.9916151
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
test ses1 ses2
( 1) [general]ses1 = 0
( 2) [vocation]ses1 = 0
( 3) [general]ses2 = 0
( 4) [vocation]ses2 = 0
chi2( 4) = 15.67
Prob > chi2 = 0.0035
Final Model: Three Predictors
mlogit prog read female ses1 ses2
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -180.65991
Iteration 2: log likelihood = -179.41794
Iteration 3: log likelihood = -179.38722
Iteration 4: log likelihood = -179.38719
Multinomial logistic regression Number of obs = 200
LR chi2(8) = 49.42
Prob > chi2 = 0.0000
Log likelihood = -179.38719 Pseudo R2 = 0.1211
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
read | -.0622009 .020823 -2.99 0.003 -.1030132 -.0213887
female | -.2907466 .3827223 -0.76 0.447 -1.040869 .4593754
ses1 | 1.053428 .5290998 1.99 0.046 .0164118 2.090445
ses2 | .5927571 .4697164 1.26 0.207 -.3278702 1.513384
_cons | 2.057293 1.205372 1.71 0.088 -.3051927 4.419779
-------------+----------------------------------------------------------------
vocation |
read | -.1153246 .0235584 -4.90 0.000 -.1614982 -.069151
female | -.2128803 .3916879 -0.54 0.587 -.9805745 .5548139
ses1 | .7672021 .6016694 1.28 0.202 -.4120482 1.946452
ses2 | 1.222412 .50843 2.40 0.016 .2259076 2.218917
_cons | 4.415091 1.272291 3.47 0.001 1.921447 6.908735
------------------------------------------------------------------------------
(Outcome prog==academic is the comparison group)
test ses1 ses2
( 1) [general]ses1 = 0
( 2) [vocation]ses1 = 0
( 3) [general]ses2 = 0
( 4) [vocation]ses2 = 0
chi2( 4) = 9.88
Prob > chi2 = 0.0424
listcoef
mlogit (N=200): Factor Change in the Odds of prog
Variable: read (sd= 10)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.05312 2.117 0.034 1.0546 1.7240
general -academic | -0.06220 -2.987 0.003 0.9397 0.5285
vocation-general | -0.05312 -2.117 0.034 0.9483 0.5800
vocation-academic | -0.11532 -4.895 0.000 0.8911 0.3065
academic-general | 0.06220 2.987 0.003 1.0642 1.8922
academic-vocation | 0.11532 4.895 0.000 1.1222 3.2622
----------------------------------------------------------------
Variable: female (sd= .5)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | -0.07787 -0.181 0.856 0.9251 0.9619
general -academic | -0.29075 -0.760 0.447 0.7477 0.8649
vocation-general | 0.07787 0.181 0.856 1.0810 1.0396
vocation-academic | -0.21288 -0.543 0.587 0.8083 0.8992
academic-general | 0.29075 0.760 0.447 1.3374 1.1562
academic-vocation | 0.21288 0.543 0.587 1.2372 1.1121
----------------------------------------------------------------
Variable: ses1 (sd= .43)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | 0.28623 0.435 0.663 1.3314 1.1294
general -academic | 1.05343 1.991 0.046 2.8675 1.5648
vocation-general | -0.28623 -0.435 0.663 0.7511 0.8854
vocation-academic | 0.76720 1.275 0.202 2.1537 1.3856
academic-general | -1.05343 -1.991 0.046 0.3487 0.6390
academic-vocation | -0.76720 -1.275 0.202 0.4643 0.7217
----------------------------------------------------------------
Variable: ses2 (sd= .5)
Odds comparing|
Group 1 vs Group 2| b z P>|z| e^b e^bStdX
------------------+---------------------------------------------
general -vocation | -0.62966 -1.070 0.285 0.5328 0.7296
general -academic | 0.59276 1.262 0.207 1.8090 1.3455
vocation-general | 0.62966 1.070 0.285 1.8770 1.3706
vocation-academic | 1.22241 2.404 0.016 3.3954 1.8441
academic-general | -0.59276 -1.262 0.207 0.5528 0.7432
academic-vocation | -1.22241 -2.404 0.016 0.2945 0.5423
----------------------------------------------------------------
fitstat
Measures of Fit for mlogit of prog
Log-Lik Intercept Only: -204.097 Log-Lik Full Model: -179.387
D(190): 358.774 LR(8): 49.419
Prob > LR: 0.000
McFadden's R2: 0.121 McFadden's Adj R2: 0.072
Maximum Likelihood R2: 0.219 Cragg & Uhler's R2: 0.252
Count R2: 0.600 Adj Count R2: 0.158
AIC: 1.894 AIC*n: 378.774
BIC: -647.906 BIC': -7.032
prchange
mlogit: Changes in Predicted Probabilities for prog
read
Avg|Chg| general vocation academic
Min->Max .52036717 -.12611925 -.65443153 .78055075
-+1/2 .01433793 -.00555836 -.01594852 .02150691
-+sd/2 .14485034 -.0548842 -.16239132 .2172755
MargEfct .01433996 -.00556038 -.01594956 .02150994
female
Avg|Chg| general vocation academic
0->1 .0420265 -.0426095 -.02043028 .06303972
ses1
Avg|Chg| general vocation academic
0->1 .1515191 .16208567 .065193 -.22727865
ses2
Avg|Chg| general vocation academic
0->1 .14467938 .04344329 .17357577 -.21701908
general vocation academic
Pr(y|x) .24157889 .20947559 .54894555
read female ses1 ses2
x= 52.23 .545 .235 .475
sd(x)= 10.2529 .49922 .425063 .500628
prtab read female, x(ses1=0 ses2=1)
mlogit: Predicted probabilities for prog
Predicted probability of outcome 1 (general)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.1699 0.1566
31 | 0.1884 0.1730
34 | 0.2064 0.1885
35 | 0.2122 0.1933
36 | 0.2177 0.1979
37 | 0.2230 0.2021
39 | 0.2327 0.2097
41 | 0.2409 0.2156
42 | 0.2443 0.2178
43 | 0.2472 0.2196
44 | 0.2496 0.2208
45 | 0.2514 0.2214
46 | 0.2527 0.2215
47 | 0.2533 0.2211
48 | 0.2533 0.2200
50 | 0.2515 0.2163
52 | 0.2471 0.2104
53 | 0.2441 0.2067
54 | 0.2405 0.2027
55 | 0.2364 0.1982
57 | 0.2268 0.1882
60 | 0.2097 0.1715
61 | 0.2034 0.1656
63 | 0.1903 0.1536
65 | 0.1768 0.1416
66 | 0.1700 0.1356
68 | 0.1565 0.1239
71 | 0.1369 0.1073
73 | 0.1245 0.0971
76 | 0.1072 0.0830
--------------------------
Predicted probability of outcome 3 (vocation)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.7616 0.7589
31 | 0.7200 0.7146
34 | 0.6727 0.6639
35 | 0.6556 0.6456
36 | 0.6379 0.6267
37 | 0.6196 0.6071
39 | 0.5814 0.5662
41 | 0.5411 0.5235
42 | 0.5204 0.5016
43 | 0.4994 0.4795
44 | 0.4781 0.4572
45 | 0.4567 0.4348
46 | 0.4352 0.4125
47 | 0.4137 0.3903
48 | 0.3924 0.3684
50 | 0.3502 0.3256
52 | 0.3095 0.2848
53 | 0.2899 0.2654
54 | 0.2709 0.2467
55 | 0.2525 0.2288
57 | 0.2178 0.1954
60 | 0.1717 0.1518
61 | 0.1579 0.1390
63 | 0.1329 0.1159
65 | 0.1110 0.0961
66 | 0.1012 0.0873
68 | 0.0838 0.0717
71 | 0.0625 0.0530
73 | 0.0511 0.0431
76 | 0.0375 0.0314
--------------------------
Predicted probability of outcome 2 (academic)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.0685 0.0845
31 | 0.0915 0.1124
34 | 0.1209 0.1476
35 | 0.1322 0.1611
36 | 0.1444 0.1755
37 | 0.1574 0.1908
39 | 0.1860 0.2241
41 | 0.2180 0.2609
42 | 0.2353 0.2806
43 | 0.2534 0.3010
44 | 0.2722 0.3221
45 | 0.2918 0.3437
46 | 0.3121 0.3660
47 | 0.3330 0.3886
48 | 0.3543 0.4116
50 | 0.3983 0.4582
52 | 0.4433 0.5048
53 | 0.4660 0.5279
54 | 0.4886 0.5506
55 | 0.5111 0.5730
57 | 0.5554 0.6164
60 | 0.6187 0.6767
61 | 0.6387 0.6954
63 | 0.6768 0.7305
65 | 0.7121 0.7624
66 | 0.7287 0.7771
68 | 0.7597 0.8044
71 | 0.8006 0.8397
73 | 0.8244 0.8599
76 | 0.8553 0.8857
--------------------------
read female ses1 ses2
x= 52.23 .545 0 1