The purpose of this seminar is to give users an introduction to analyzing ordinal logistic models using Stata. In addition to the built-in Stata commands we will be demonstrating the use of a number on user-written ado’s, in particular, gologit, listcoef, fitstat, prchange, prtab, etc. To find out more about these programs or to download them type search followed by the program name in the Stata command window (example: search gologit). These add-on programs ease the running and interpretation of ordinal logistic models.
Binary Response Variable Example
Let’s begin with an example using a binary response variable. We will see that the results of an ordinal logistic model are the same as for a traditional logistic model with the exception that there is a cut point instead of a constant.
use http://www.gseis.ucla.edu/courses/data/honors, clear
logit honors female
Iteration 0: log likelihood = -115.64441
Iteration 1: log likelihood = -113.68907
Iteration 2: log likelihood = -113.67691
Iteration 3: log likelihood = -113.6769
Logit estimates Number of obs = 200
LR chi2(1) = 3.94
Prob > chi2 = 0.0473
Log likelihood = -113.6769 Pseudo R2 = 0.0170
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | .6513707 .3336752 1.95 0.051 -.0026207 1.305362
_cons | -1.400088 .2631619 -5.32 0.000 -1.915876 -.8842998
------------------------------------------------------------------------------
ologit honors female
Iteration 0: log likelihood = -115.64441
Iteration 1: log likelihood = -113.68907
Iteration 2: log likelihood = -113.67691
Iteration 3: log likelihood = -113.6769
Ordered logit estimates Number of obs = 200
LR chi2(1) = 3.94
Prob > chi2 = 0.0473
Log likelihood = -113.6769 Pseudo R2 = 0.0170
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | .6513707 .3336752 1.95 0.051 -.0026207 1.305362
-------------+----------------------------------------------------------------
_cut1 | 1.400088 .2631619 (Ancillary parameter)
------------------------------------------------------------------------------
predict p0 p1
(option p assumed; predicted probabilities)
list female honors p0 p1 in 1/20, nolabel
+---------------------------------------+
| female honors p0 p1 |
|---------------------------------------|
1. | 1 0 .6788991 .3211009 |
2. | 0 0 .8021978 .1978022 |
3. | 0 0 .8021978 .1978022 |
4. | 1 1 .6788991 .3211009 |
5. | 1 1 .6788991 .3211009 |
|---------------------------------------|
6. | 0 0 .8021978 .1978022 |
7. | 1 0 .6788991 .3211009 |
8. | 1 0 .6788991 .3211009 |
9. | 1 0 .6788991 .3211009 |
10. | 1 0 .6788991 .3211009 |
|---------------------------------------|
11. | 1 1 .6788991 .3211009 |
12. | 0 0 .8021978 .1978022 |
13. | 0 0 .8021978 .1978022 |
14. | 1 0 .6788991 .3211009 |
15. | 1 0 .6788991 .3211009 |
|---------------------------------------|
16. | 1 0 .6788991 .3211009 |
17. | 0 0 .8021978 .1978022 |
18. | 1 0 .6788991 .3211009 |
19. | 1 1 .6788991 .3211009 |
20. | 1 0 .6788991 .3211009 |
+---------------------------------------+
3-Category Response Variable Example
use http://www.gseis.ucla.edu/courses/data/hsb2, clear
(highschool and beyond (200 cases))
codebook ses
----------------------------------------------------------------------------------------------------------
ses (unlabeled)
----------------------------------------------------------------------------------------------------------
type: numeric (float)
label: sl
range: [1,3] units: 1
unique values: 3 missing .: 0/200
tabulation: Freq. Numeric Label
47 1 low
95 2 middle
58 3 high
ologit ses female
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -209.07664
Iteration 2: log likelihood = -209.07448
Ordered logit estimates Number of obs = 200
LR chi2(1) = 3.02
Prob > chi2 = 0.0824
Log likelihood = -209.07448 Pseudo R2 = 0.0072
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -.4631078 .267655 -1.73 0.084 -.9877019 .0614863
-------------+----------------------------------------------------------------
_cut1 | -1.439902 .2274731 (Ancillary parameters)
_cut2 | .6611402 .2049573
------------------------------------------------------------------------------
The omodel command by Rory Wolfe and Bill Gould is used to test the proportional odds assumption.
omodel logit ses female
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -209.07664
Iteration 2: log likelihood = -209.07448
Ordered logit estimates Number of obs = 200
LR chi2(1) = 3.02
Prob > chi2 = 0.0824
Log likelihood = -209.07448 Pseudo R2 = 0.0072
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -.4631078 .267655 -1.73 0.084 -.9877019 .0614863
-------------+----------------------------------------------------------------
_cut1 | -1.439902 .2274731 (Ancillary parameters)
_cut2 | .6611402 .2049573
------------------------------------------------------------------------------
Approximate likelihood-ratio test of proportionality of odds
across response categories:
chi2(1) = 1.67
Prob > chi2 = 0.1966
The gologit command by Vincent Kang Fu of UCLA performs a generalized ordinal logistic regression. This command shows the underlying multiequation nature of ordinal logistic models.
gologit ses female
Iteration 0: Log Likelihood = -210.58254
Iteration 1: Log Likelihood = -208.2693
Iteration 2: Log Likelihood = -208.24309
Iteration 3: Log Likelihood = -208.24309
Iteration 4: Log Likelihood = -208.24309
Generalized Ordered Logit Estimates Number of obs = 200
Model chi2(2) = 4.68
Prob > chi2 = 0.0964
Log Likelihood = -208.2430884 Pseudo R2 = 0.0111
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mleq1 |
female | -.7446136 .3522238 -2.11 0.035 -1.43496 -.0542677
_cons | 1.622683 .2825324 5.74 0.000 1.06893 2.176437
-------------+----------------------------------------------------------------
mleq2 |
female | -.2548923 .3124013 -0.82 0.415 -.8671875 .357403
_cons | -.7598386 .2249706 -3.38 0.001 -1.200773 -.3189042
------------------------------------------------------------------------------
test [mleq1=mleq2]
( 1) [mleq1]female - [mleq2]female = 0
chi2( 1) = 1.62
Prob > chi2 = 0.2025
Let’s rerun the original ologit model.
ologit ses female
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -209.07664
Iteration 2: log likelihood = -209.07448
Ordered logit estimates Number of obs = 200
LR chi2(1) = 3.02
Prob > chi2 = 0.0824
Log likelihood = -209.07448 Pseudo R2 = 0.0072
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -.4631078 .267655 -1.73 0.084 -.9877019 .0614863
-------------+----------------------------------------------------------------
_cut1 | -1.439902 .2274731 (Ancillary parameters)
_cut2 | .6611402 .2049573
------------------------------------------------------------------------------
Next, we look at some of the Long & Freese utilities.
listcoef
ologit (N=200): Factor Change in Odds
Odds of: >m vs <=m ---------------------------------------------------------------------- ses | b z P>|z| e^b e^bStdX SDofX
-------------+--------------------------------------------------------
female | -0.46311 -1.730 0.084 0.6293 0.7936 0.4992
----------------------------------------------------------------------
listcoef, percent
ologit (N=200): Percentage Change in Odds
Odds of: >m vs <=m ---------------------------------------------------------------------- ses | b z P>|z| % %StdX SDofX
-------------+--------------------------------------------------------
female | -0.46311 -1.730 0.084 -37.1 -20.6 0.4992
----------------------------------------------------------------------
fitstat
Measures of Fit for ologit of ses
Log-Lik Intercept Only: -210.583 Log-Lik Full Model: -209.074
D(197): 418.149 LR(1): 3.016
Prob > LR: 0.082
McFadden's R2: 0.007 McFadden's Adj R2: -0.007
Maximum Likelihood R2: 0.015 Cragg & Uhler's R2: 0.017
McKelvey and Zavoina's R2: 0.016
Variance of y*: 3.343 Variance of error: 3.290
Count R2: 0.475 Adj Count R2: 0.000
AIC: 2.121 AIC*n: 424.149
BIC: -625.620 BIC': 2.282
prchange
ologit: Changes in Predicted Probabilities for ses
female
Avg|Chg| low middle high
0->1 .06350623 .0819678 .01329154 -.09525935
low middle high
Pr(y|x) .23370479 .48001799 .2862772
female
x= .545
sd(x)= .49922
prtab female
ologit: Predicted probabilities for ses
Predicted probability of outcome 1 (low)
----------------------
female | Prediction
----------+-----------
male | 0.1916
female | 0.2735
----------------------
Predicted probability of outcome 2 (middle)
----------------------
female | Prediction
----------+-----------
male | 0.4680
female | 0.4812
----------------------
Predicted probability of outcome 3 (high)
----------------------
female | Prediction
----------+-----------
male | 0.3405
female | 0.2452
----------------------
female
x= .545
predict p1 p2 p3
(option p assumed; predicted probabilities)
list female ses p1 p2 p3 in 1/20, nolabel
+-----------------------------------------------+
| female ses p1 p2 p3 |
|-----------------------------------------------|
1. | 0 1 .1915604 .467956 .3404835 |
2. | 1 2 .2735282 .4812476 .2452242 |
3. | 0 3 .1915604 .467956 .3404835 |
4. | 0 3 .1915604 .467956 .3404835 |
5. | 0 2 .1915604 .467956 .3404835 |
|-----------------------------------------------|
6. | 0 2 .1915604 .467956 .3404835 |
7. | 0 2 .1915604 .467956 .3404835 |
8. | 0 2 .1915604 .467956 .3404835 |
9. | 0 2 .1915604 .467956 .3404835 |
10. | 0 2 .1915604 .467956 .3404835 |
|-----------------------------------------------|
11. | 0 2 .1915604 .467956 .3404835 |
12. | 0 2 .1915604 .467956 .3404835 |
13. | 0 3 .1915604 .467956 .3404835 |
14. | 0 3 .1915604 .467956 .3404835 |
15. | 0 1 .1915604 .467956 .3404835 |
|-----------------------------------------------|
16. | 0 1 .1915604 .467956 .3404835 |
17. | 0 3 .1915604 .467956 .3404835 |
18. | 0 2 .1915604 .467956 .3404835 |
19. | 0 3 .1915604 .467956 .3404835 |
20. | 0 2 .1915604 .467956 .3404835 |
+-----------------------------------------------+
An Example Using a Continuous Predictor
drop p1 p2 p3
ologit ses read
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -201.46192
Iteration 2: log likelihood = -201.38992
Iteration 3: log likelihood = -201.38986
Ordered logit estimates Number of obs = 200
LR chi2(1) = 18.39
Prob > chi2 = 0.0000
Log likelihood = -201.38986 Pseudo R2 = 0.0437
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .0579174 .0138283 4.19 0.000 .0308145 .0850203
-------------+----------------------------------------------------------------
_cut1 | 1.755299 .7125267 (Ancillary parameters)
_cut2 | 3.986354 .7626725
------------------------------------------------------------------------------
listcoef
ologit (N=200): Factor Change in Odds
Odds of: >m vs <=m ---------------------------------------------------------------------- ses | b z P>|z| e^b e^bStdX SDofX
-------------+--------------------------------------------------------
read | 0.05792 4.188 0.000 1.0596 1.8109 10.2529
----------------------------------------------------------------------
fitstat
Measures of Fit for ologit of ses
Log-Lik Intercept Only: -210.583 Log-Lik Full Model: -201.390
D(197): 402.780 LR(1): 18.385
Prob > LR: 0.000
McFadden's R2: 0.044 McFadden's Adj R2: 0.029
Maximum Likelihood R2: 0.088 Cragg & Uhler's R2: 0.100
McKelvey and Zavoina's R2: 0.097
Variance of y*: 3.642 Variance of error: 3.290
Count R2: 0.500 Adj Count R2: 0.048
AIC: 2.044 AIC*n: 408.780
BIC: -640.989 BIC': -13.087
predict p1 p2 p3
(option p assumed; predicted probabilities)
list read ses p1 p2 p3 in 1/20, nolabel
+---------------------------------------------+
| read ses p1 p2 p3 |
|---------------------------------------------|
1. | 57 1 .1756661 .4892019 .3351319 |
2. | 68 2 .1012801 .4107109 .488009 |
3. | 44 3 .311511 .4966322 .1918568 |
4. | 63 3 .1308465 .4527512 .4164023 |
5. | 47 2 .2755154 .5042394 .2202452 |
|---------------------------------------------|
6. | 44 2 .311511 .4966322 .1918568 |
7. | 50 2 .2422159 .5062573 .2515268 |
8. | 34 2 .4467301 .4358573 .1174126 |
9. | 63 2 .1308465 .4527512 .4164023 |
10. | 57 2 .1756661 .4892019 .3351319 |
|---------------------------------------------|
11. | 60 2 .1519043 .4732097 .374886 |
12. | 57 2 .1756661 .4892019 .3351319 |
13. | 73 3 .0777966 .3620922 .5601112 |
14. | 54 3 .2022584 .5001549 .2975867 |
15. | 45 1 .2992269 .4997758 .2009973 |
|---------------------------------------------|
16. | 42 1 .3368798 .4885857 .1745345 |
17. | 47 3 .2755154 .5042394 .2202452 |
18. | 57 2 .1756661 .4892019 .3351319 |
19. | 68 3 .1012801 .4107109 .488009 |
20. | 55 2 .1930744 .4970924 .3098333 |
+---------------------------------------------+
sort read
scatter p1 p2 p3 read, connect(l l l) msym(i i i)
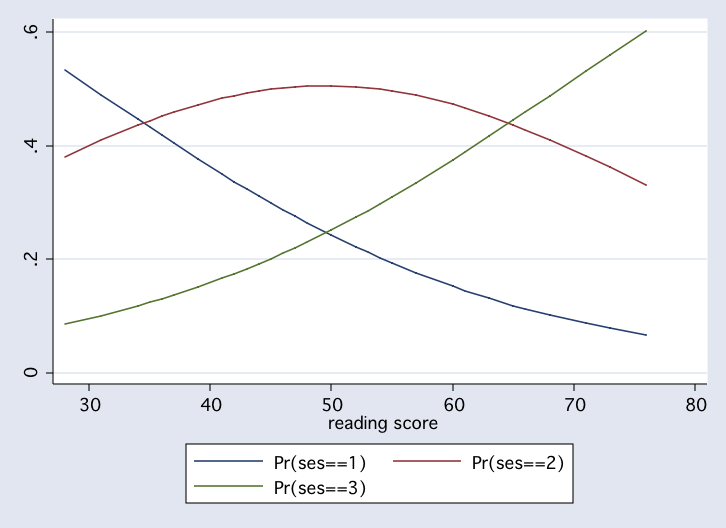list read ses p1 p2 p3 if p1>p2, nolabel
+---------------------------------------------+
| read ses p1 p2 p3 |
|---------------------------------------------|
1. | 28 1 .5333536 .3807395 .0859069 |
2. | 31 2 .4899665 .4094642 .1005692 |
3. | 34 2 .4467301 .4358573 .1174126 |
4. | 34 2 .4467301 .4358573 .1174126 |
5. | 34 2 .4467301 .4358573 .1174126 |
|---------------------------------------------|
6. | 34 3 .4467301 .4358573 .1174126 |
7. | 34 1 .4467301 .4358573 .1174126 |
8. | 34 1 .4467301 .4358573 .1174126 |
+---------------------------------------------+
list read ses p1 p2 p3 if p1>p2 & p1>p3, nolabel
+---------------------------------------------+
| read ses p1 p2 p3 |
|---------------------------------------------|
1. | 28 1 .5333536 .3807395 .0859069 |
2. | 31 2 .4899665 .4094642 .1005692 |
3. | 34 2 .4467301 .4358573 .1174126 |
4. | 34 2 .4467301 .4358573 .1174126 |
5. | 34 2 .4467301 .4358573 .1174126 |
|---------------------------------------------|
6. | 34 3 .4467301 .4358573 .1174126 |
7. | 34 1 .4467301 .4358573 .1174126 |
8. | 34 1 .4467301 .4358573 .1174126 |
+---------------------------------------------+
drop p1 p2 p3
Here are some more of the Long & Freeze utilities.
prchange
ologit: Changes in Predicted Probabilities for ses
read
Avg|Chg| low middle high
Min->Max .34431122 -.46714365 -.04932317 .51646684
-+1/2 .00772587 -.00991599 -.0016728 .01158881
-+sd/2 .07898068 -.10162368 -.01684734 .11847103
MargEfct .00772609 -.00991603 -.00167311 .01158914
low middle high
Pr(y|x) .21930437 .50408369 .27661195
read
x= 52.23
sd(x)= 10.2529
prtab read
ologit: Predicted probabilities for ses
Predicted probability of outcome 1 (low)
----------------------
reading |
score | Prediction
----------+-----------
28 | 0.5334
31 | 0.4900
34 | 0.4467
35 | 0.4325
36 | 0.4183
37 | 0.4043
39 | 0.3767
41 | 0.3499
42 | 0.3369
43 | 0.3241
44 | 0.3115
45 | 0.2992
46 | 0.2872
47 | 0.2755
48 | 0.2641
50 | 0.2422
52 | 0.2216
53 | 0.2118
54 | 0.2023
55 | 0.1931
57 | 0.1757
60 | 0.1519
61 | 0.1446
63 | 0.1308
65 | 0.1182
66 | 0.1123
68 | 0.1013
71 | 0.0865
73 | 0.0778
76 | 0.0662
----------------------
Predicted probability of outcome 2 (middle)
----------------------
reading |
score | Prediction
----------+-----------
28 | 0.3807
31 | 0.4095
34 | 0.4359
35 | 0.4440
36 | 0.4517
37 | 0.4591
39 | 0.4724
41 | 0.4837
42 | 0.4886
43 | 0.4929
44 | 0.4966
45 | 0.4998
46 | 0.5023
47 | 0.5042
48 | 0.5055
50 | 0.5063
52 | 0.5045
53 | 0.5026
54 | 0.5002
55 | 0.4971
57 | 0.4892
60 | 0.4732
61 | 0.4669
63 | 0.4528
65 | 0.4370
66 | 0.4285
68 | 0.4107
71 | 0.3821
73 | 0.3621
76 | 0.3314
----------------------
Predicted probability of outcome 3 (high)
----------------------
reading |
score | Prediction
----------+-----------
28 | 0.0859
31 | 0.1006
34 | 0.1174
35 | 0.1235
36 | 0.1300
37 | 0.1366
39 | 0.1509
41 | 0.1663
42 | 0.1745
43 | 0.1830
44 | 0.1919
45 | 0.2010
46 | 0.2105
47 | 0.2202
48 | 0.2304
50 | 0.2515
52 | 0.2740
53 | 0.2856
54 | 0.2976
55 | 0.3098
57 | 0.3351
60 | 0.3749
61 | 0.3886
63 | 0.4164
65 | 0.4448
66 | 0.4591
68 | 0.4880
71 | 0.5314
73 | 0.5601
76 | 0.6024
----------------------
read
x= 52.23
A Two Predictor Example
ologit ses read female
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -200.28305
Iteration 2: log likelihood = -200.18917
Iteration 3: log likelihood = -200.18906
Ordered logit estimates Number of obs = 200
LR chi2(2) = 20.79
Prob > chi2 = 0.0000
Log likelihood = -200.18906 Pseudo R2 = 0.0494
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .05714 .0138643 4.12 0.000 .0299665 .0843134
female | -.4195397 .2715105 -1.55 0.122 -.9516905 .1126111
-------------+----------------------------------------------------------------
_cut1 | 1.477402 .7343098 (Ancillary parameters)
_cut2 | 3.730551 .7791244
------------------------------------------------------------------------------
listcoef
ologit (N=200): Factor Change in Odds
Odds of: >m vs <=m ---------------------------------------------------------------------- ses | b z P>|z| e^b e^bStdX SDofX
-------------+--------------------------------------------------------
read | 0.05714 4.121 0.000 1.0588 1.7965 10.2529
female | -0.41954 -1.545 0.122 0.6573 0.8110 0.4992
----------------------------------------------------------------------
fitstat
Measures of Fit for ologit of ses
Log-Lik Intercept Only: -210.583 Log-Lik Full Model: -200.189
D(196): 400.378 LR(2): 20.787
Prob > LR: 0.000
McFadden's R2: 0.049 McFadden's Adj R2: 0.030
Maximum Likelihood R2: 0.099 Cragg & Uhler's R2: 0.112
McKelvey and Zavoina's R2: 0.108
Variance of y*: 3.690 Variance of error: 3.290
Count R2: 0.500 Adj Count R2: 0.048
AIC: 2.042 AIC*n: 408.378
BIC: -638.092 BIC': -10.190
prtab read female
ologit: Predicted probabilities for ses
Predicted probability of outcome 1 (low)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.4694 0.5737
31 | 0.4270 0.5314
34 | 0.3857 0.4885
35 | 0.3723 0.4743
36 | 0.3590 0.4601
37 | 0.3460 0.4459
39 | 0.3206 0.4179
41 | 0.2962 0.3904
42 | 0.2845 0.3769
43 | 0.2730 0.3635
44 | 0.2618 0.3504
45 | 0.2509 0.3375
46 | 0.2403 0.3249
47 | 0.2300 0.3125
48 | 0.2201 0.3003
50 | 0.2011 0.2769
52 | 0.1833 0.2546
53 | 0.1749 0.2439
54 | 0.1668 0.2335
55 | 0.1591 0.2234
57 | 0.1444 0.2042
60 | 0.1244 0.1778
61 | 0.1184 0.1696
63 | 0.1069 0.1541
65 | 0.0965 0.1398
66 | 0.0916 0.1330
68 | 0.0826 0.1204
71 | 0.0705 0.1034
73 | 0.0633 0.0933
76 | 0.0539 0.0798
--------------------------
Predicted probability of outcome 2 (middle)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.4244 0.3539
31 | 0.4494 0.3838
34 | 0.4709 0.4124
35 | 0.4772 0.4214
36 | 0.4830 0.4302
37 | 0.4883 0.4386
39 | 0.4973 0.4544
41 | 0.5040 0.4687
42 | 0.5065 0.4751
43 | 0.5084 0.4811
44 | 0.5097 0.4866
45 | 0.5103 0.4915
46 | 0.5104 0.4959
47 | 0.5098 0.4998
48 | 0.5086 0.5030
50 | 0.5044 0.5078
52 | 0.4979 0.5102
53 | 0.4937 0.5104
54 | 0.4890 0.5100
55 | 0.4838 0.5091
57 | 0.4719 0.5053
60 | 0.4505 0.4952
61 | 0.4426 0.4907
63 | 0.4257 0.4801
65 | 0.4076 0.4675
66 | 0.3982 0.4606
68 | 0.3788 0.4454
71 | 0.3487 0.4199
73 | 0.3282 0.4014
76 | 0.2977 0.3723
--------------------------
Predicted probability of outcome 3 (high)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.1062 0.0724
31 | 0.1236 0.0848
34 | 0.1433 0.0991
35 | 0.1505 0.1043
36 | 0.1580 0.1098
37 | 0.1657 0.1155
39 | 0.1821 0.1277
41 | 0.1998 0.1410
42 | 0.2090 0.1480
43 | 0.2187 0.1554
44 | 0.2286 0.1630
45 | 0.2388 0.1710
46 | 0.2493 0.1792
47 | 0.2602 0.1878
48 | 0.2713 0.1966
50 | 0.2945 0.2153
52 | 0.3188 0.2353
53 | 0.3313 0.2457
54 | 0.3441 0.2564
55 | 0.3571 0.2675
57 | 0.3838 0.2905
60 | 0.4250 0.3270
61 | 0.4391 0.3397
63 | 0.4674 0.3658
65 | 0.4959 0.3927
66 | 0.5102 0.4064
68 | 0.5387 0.4342
71 | 0.5809 0.4767
73 | 0.6084 0.5053
76 | 0.6484 0.5480
--------------------------
read female
x= 52.23 .545
3-Category Predictor Example
tabulate prog, gen(prog)
type of |
program | Freq. Percent Cum.
------------+-----------------------------------
general | 45 22.50 22.50
academic | 105 52.50 75.00
vocation | 50 25.00 100.00
------------+-----------------------------------
Total | 200 100.00
ologit ses prog1 prog2
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -204.59144
Iteration 2: log likelihood = -204.554
Iteration 3: log likelihood = -204.55398
Ordered logit estimates Number of obs = 200
LR chi2(2) = 12.06
Prob > chi2 = 0.0024
Log likelihood = -204.55398 Pseudo R2 = 0.0286
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog1 | -.180289 .382671 -0.47 0.638 -.9303103 .5697323
prog2 | .8500258 .3223129 2.64 0.008 .2183042 1.481747
-------------+----------------------------------------------------------------
_cut1 | -.8456498 .2679547 (Ancillary parameters)
_cut2 | 1.335285 .2806444
------------------------------------------------------------------------------
test prog1 prog2
( 1) prog1 = 0
( 2) prog2 = 0
chi2( 2) = 11.69
Prob > chi2 = 0.0029
I prefer to use the academic group as the reference group and so will use prog1 and prog2 in the model.
ologit ses prog1 prog3
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -204.59144
Iteration 2: log likelihood = -204.554
Iteration 3: log likelihood = -204.55398
Ordered logit estimates Number of obs = 200
LR chi2(2) = 12.06
Prob > chi2 = 0.0024
Log likelihood = -204.55398 Pseudo R2 = 0.0286
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog1 | -1.030315 .3479667 -2.96 0.003 -1.712317 -.3483126
prog3 | -.8500258 .3223129 -2.64 0.008 -1.481747 -.2183042
-------------+----------------------------------------------------------------
_cut1 | -1.695676 .2334022 (Ancillary parameters)
_cut2 | .4852592 .195606
------------------------------------------------------------------------------
test prog1 prog3
( 1) prog1 = 0
( 2) prog3 = 0
chi2( 2) = 11.69
Prob > chi2 = 0.0029
Our Final Model: Three Predictors
ologit ses read female prog1 prog3
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -197.79263
Iteration 2: log likelihood = -197.63977
Iteration 3: log likelihood = -197.63946
Ordered logit estimates Number of obs = 200
LR chi2(4) = 25.89
Prob > chi2 = 0.0000
Log likelihood = -197.63946 Pseudo R2 = 0.0615
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .0481912 .0149969 3.21 0.001 .0187979 .0775846
female | -.444623 .2725877 -1.63 0.103 -.9788851 .0896391
prog1 | -.7946682 .3597171 -2.21 0.027 -1.499701 -.0896357
prog3 | -.4294622 .3493735 -1.23 0.219 -1.114222 .2552972
-------------+----------------------------------------------------------------
_cut1 | .682197 .8619888 (Ancillary parameters)
_cut2 | 2.983569 .8891324
------------------------------------------------------------------------------
test prog1 prog3
( 1) prog1 = 0
( 2) prog3 = 0
chi2( 2) = 5.04
Prob > chi2 = 0.0803
listcoef
ologit (N=200): Factor Change in Odds
Odds of: >m vs <=m ---------------------------------------------------------------------- ses | b z P>|z| e^b e^bStdX SDofX
-------------+--------------------------------------------------------
read | 0.04819 3.213 0.001 1.0494 1.6390 10.2529
female | -0.44462 -1.631 0.103 0.6411 0.8009 0.4992
prog1 | -0.79467 -2.209 0.027 0.4517 0.7170 0.4186
prog3 | -0.42946 -1.229 0.219 0.6509 0.8299 0.4341
----------------------------------------------------------------------
fitstat
Measures of Fit for ologit of ses
Log-Lik Intercept Only: -210.583 Log-Lik Full Model: -197.639
D(194): 395.279 LR(4): 25.886
Prob > LR: 0.000
McFadden's R2: 0.061 McFadden's Adj R2: 0.033
Maximum Likelihood R2: 0.121 Cragg & Uhler's R2: 0.138
McKelvey and Zavoina's R2: 0.135
Variance of y*: 3.805 Variance of error: 3.290
Count R2: 0.520 Adj Count R2: 0.086
AIC: 2.036 AIC*n: 407.279
BIC: -632.595 BIC': -4.693
prchange
ologit: Changes in Predicted Probabilities for ses
read
Avg|Chg| low middle high
Min->Max .28959884 -.38608418 -.04831406 .43439826
-+1/2 .00633105 -.00808108 -.00141549 .00949657
-+sd/2 .06479194 -.082848 -.01433992 .09718789
MargEfct .00633115 -.00808108 -.00141564 .00949672
female
Avg|Chg| low middle high
0->1 .05885413 .07370418 .01457703 -.08828117
prog1
Avg|Chg| low middle high
0->1 .09951697 .14927547 -.00917467 -.14010078
prog3
Avg|Chg| low middle high
0->1 .05353026 .07640016 .00389522 -.08029538
low middle high
Pr(y|x) .21309914 .51698065 .2699202
read female prog1 prog3
x= 52.23 .545 .225 .25
sd(x)= 10.2529 .49922 .41863 .434099
prtab read female, x(prog1=0 prog3=0)
ologit: Predicted probabilities for ses
Predicted probability of outcome 1 (low)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.3391 0.4446
31 | 0.3075 0.4092
34 | 0.2776 0.3748
35 | 0.2681 0.3636
36 | 0.2587 0.3525
37 | 0.2496 0.3416
39 | 0.2320 0.3202
41 | 0.2152 0.2996
42 | 0.2072 0.2896
43 | 0.1994 0.2798
44 | 0.1918 0.2702
45 | 0.1845 0.2608
46 | 0.1773 0.2516
47 | 0.1704 0.2427
48 | 0.1637 0.2339
50 | 0.1509 0.2171
52 | 0.1390 0.2011
53 | 0.1333 0.1935
54 | 0.1278 0.1861
55 | 0.1226 0.1789
57 | 0.1126 0.1652
60 | 0.0989 0.1462
61 | 0.0947 0.1403
63 | 0.0868 0.1291
65 | 0.0794 0.1186
66 | 0.0760 0.1137
68 | 0.0695 0.1043
71 | 0.0607 0.0916
73 | 0.0554 0.0839
76 | 0.0483 0.0734
--------------------------
Predicted probability of outcome 2 (middle)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.4976 0.4442
31 | 0.5085 0.4645
34 | 0.5157 0.4821
35 | 0.5173 0.4873
36 | 0.5184 0.4922
37 | 0.5190 0.4966
39 | 0.5191 0.5045
41 | 0.5173 0.5107
42 | 0.5158 0.5132
43 | 0.5139 0.5153
44 | 0.5115 0.5169
45 | 0.5087 0.5181
46 | 0.5055 0.5189
47 | 0.5019 0.5193
48 | 0.4979 0.5192
50 | 0.4888 0.5176
52 | 0.4782 0.5144
53 | 0.4724 0.5121
54 | 0.4663 0.5094
55 | 0.4599 0.5063
57 | 0.4463 0.4988
60 | 0.4241 0.4848
61 | 0.4163 0.4795
63 | 0.4001 0.4677
65 | 0.3834 0.4548
66 | 0.3749 0.4479
68 | 0.3577 0.4334
71 | 0.3315 0.4101
73 | 0.3141 0.3937
76 | 0.2882 0.3683
--------------------------
Predicted probability of outcome 3 (high)
--------------------------
reading | female
score | male female
----------+---------------
28 | 0.1633 0.1112
31 | 0.1840 0.1263
34 | 0.2067 0.1431
35 | 0.2147 0.1491
36 | 0.2229 0.1553
37 | 0.2314 0.1618
39 | 0.2490 0.1753
41 | 0.2674 0.1896
42 | 0.2770 0.1972
43 | 0.2867 0.2049
44 | 0.2967 0.2129
45 | 0.3068 0.2210
46 | 0.3172 0.2295
47 | 0.3277 0.2381
48 | 0.3384 0.2469
50 | 0.3603 0.2653
52 | 0.3828 0.2845
53 | 0.3943 0.2944
54 | 0.4058 0.3045
55 | 0.4175 0.3148
57 | 0.4411 0.3360
60 | 0.4770 0.3690
61 | 0.4890 0.3802
63 | 0.5131 0.4032
65 | 0.5371 0.4266
66 | 0.5491 0.4384
68 | 0.5728 0.4623
71 | 0.6078 0.4983
73 | 0.6305 0.5224
76 | 0.6635 0.5583
--------------------------
read female prog1 prog3
x= 52.23 .545 0 0
Using linktest to test for model specification errors.
linktest
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -197.64558
Iteration 2: log likelihood = -197.49272
Iteration 3: log likelihood = -197.49241
Ordered logit estimates Number of obs = 200
LR chi2(2) = 26.18
Prob > chi2 = 0.0000
Log likelihood = -197.49241 Pseudo R2 = 0.0622
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_hat | .4784934 .9824955 0.49 0.626 -1.447162 2.404149
_hatsq | .1304895 .241209 0.54 0.589 -.3422715 .6032505
-------------+----------------------------------------------------------------
_cut1 | .2243895 .9347503 (Ancillary parameters)
_cut2 | 2.526304 .9591539
------------------------------------------------------------------------------
Here again is the test of proportional odds.
omodel logit ses read female prog1 prog3
Iteration 0: log likelihood = -210.58254
Iteration 1: log likelihood = -197.79263
Iteration 2: log likelihood = -197.63977
Iteration 3: log likelihood = -197.63946
Ordered logit estimates Number of obs = 200
LR chi2(4) = 25.89
Prob > chi2 = 0.0000
Log likelihood = -197.63946 Pseudo R2 = 0.0615
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .0481912 .0149969 3.21 0.001 .0187979 .0775846
female | -.444623 .2725877 -1.63 0.103 -.9788851 .0896391
prog1 | -.7946682 .3597171 -2.21 0.027 -1.499701 -.0896357
prog3 | -.4294622 .3493735 -1.23 0.219 -1.114222 .2552972
-------------+----------------------------------------------------------------
_cut1 | .682197 .8619888 (Ancillary parameters)
_cut2 | 2.983569 .8891324
------------------------------------------------------------------------------
Approximate likelihood-ratio test of proportionality of odds
across response categories:
chi2(4) = 6.46
Prob > chi2 = 0.1676
Let’s look at the generalized ordered logistic model.
gologit ses read female prog1 prog3
Iteration 0: Log Likelihood = -210.58254
Iteration 1: Log Likelihood = -194.98035
Iteration 2: Log Likelihood = -194.40757
Iteration 3: Log Likelihood = -194.40633
Iteration 4: Log Likelihood = -194.40633
Generalized Ordered Logit Estimates Number of obs = 200
Model chi2(8) = 32.35
Prob > chi2 = 0.0001
Log Likelihood = -194.4063269 Pseudo R2 = 0.0768
------------------------------------------------------------------------------
ses | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mleq1 |
read | .053024 .0209806 2.53 0.011 .0119028 .0941451
female | -.7215625 .3628111 -1.99 0.047 -1.432659 -.0104659
prog1 | -.6979021 .4224733 -1.65 0.099 -1.525934 .1301303
prog3 | .1012859 .4606329 0.22 0.826 -.8015381 1.00411
_cons | -.9279434 1.173037 -0.79 0.429 -3.227054 1.371167
-------------+----------------------------------------------------------------
mleq2 |
read | .0452445 .0176378 2.57 0.010 .0106751 .079814
female | -.2204975 .3273852 -0.67 0.501 -.8621607 .4211657
prog1 | -.745496 .4380499 -1.70 0.089 -1.604058 .113066
prog3 | -1.029291 .4782148 -2.15 0.031 -1.966575 -.0920073
_cons | -2.836412 1.042437 -2.72 0.007 -4.879551 -.7932731
------------------------------------------------------------------------------
test [mleq1=mleq2]
( 1) [mleq1]read - [mleq2]read = 0
( 2) [mleq1]female - [mleq2]female = 0
( 3) [mleq1]prog1 - [mleq2]prog1 = 0
( 4) [mleq1]prog3 - [mleq2]prog3 = 0
chi2( 4) = 5.91
Prob > chi2 = 0.2056