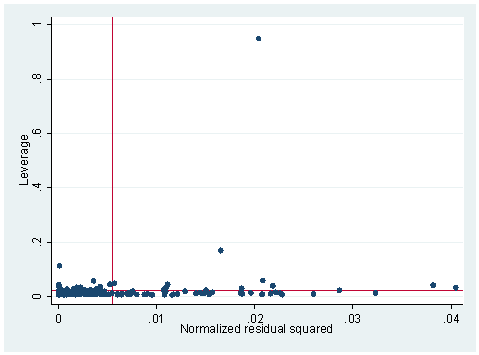
1. The following data set consists of measured weight, measured height, reported weight and reported height of some 200 people. We tried to build a model to predict measured weight by reported weight, reported height and measured height. We did an lvr2plot after the regression and here is what we have. Explain what you see in the graph and try to use other STATA commands to identify the problematic observation(s). What do you think the problem is and what is your solution?
use davis, clear regress measwt measht reptwt reptht Source | SS df MS Number of obs = 181 ---------+------------------------------ F( 3, 177) = 1640.88 Model | 40891.9594 3 13630.6531 Prob > F = 0.0000 Residual | 1470.3279 177 8.30693727 R-squared = 0.9653 ---------+------------------------------ Adj R-squared = 0.9647 Total | 42362.2873 180 235.346041 Root MSE = 2.8822 ------------------------------------------------------------------------------ measwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- measht | -.9607757 .0260189 -36.926 0.000 -1.012123 -.9094285 reptwt | 1.01917 .0240778 42.328 0.000 .971654 1.066687 reptht | .8184156 .0419658 19.502 0.000 .7355979 .9012334 _cons | 24.8138 4.888302 5.076 0.000 15.16695 34.46065 ------------------------------------------------------------------------------ lvr2plot
Answer:
lvr2plot is the leverage against residual squared plot. The upper left corner of the plot will be points that are high in leverage and the lower right corner will be points that are high in the absolute of residuals. The upper right portion will be those points that are both high in leverage and in the absolute of residuals. There is one point in this plot that stands out so much differently from any other point. There are many ways of figuring out what this point is. First of all, graphically, we can add an option in our lvr2plot command to see which observation is associated with the extreme point on the plot.
lvr2plot, ml(subject)
There are also numerical measures that we can deploy. Since it is obviously very high on leverage, we can first generate leverage and list the extreme ones.
predict l, leverage
hilo l measwt measht reptwt reptht subject, high show(5)
5 highest observations on l
l measwt measht reptwt reptht subject
0578113 65 187 67 188 40
0596073 102 185 107 185 54
1136993 76 197 75 200 19
1702566 119 180 124 178 21
9481246 166 57 56 163 12
The other way is to use Cook’s D since Cook’s D is the combination of leverage and residual.
predict c, cooksd
hilo c measwt measht reptwt reptht subject, high show(5)
5 highest observations on c
c measwt measht reptwt reptht subject
0619987 102 185 107 185 54
0628549 88 185 93 188 191
0779325 92 187 101 185 17
1808358 119 180 124 178 21
317.8551 166 57 56 163 12
We can also look at studentized residuals.
predict rstu, rstu
hilo rstu measwt measht reptwt reptht subject, show(5)
5 lowest and highest observations on rstu
rstu measwt measht reptwt reptht subject
-2.772892 88 185 93 188 191
-2.703085 92 187 101 185 17
-2.305224 84 183 90 183 111
-2.023018 53 169 52 175 83
-1.994573 102 185 107 185 54
rstu measwt measht reptwt reptht subject
2.030575 58 161 51 159 2
2.031815 75 172 70 169 59
2.176899 60 167 55 163 84
2.440577 60 172 55 168 187
10.67515 166 57 56 163 12
In all of the above, we see that subject 12 is a problematic point. Is it an entry error? Yes. Apparently for subject 12 the measured weight has been switched with measured height. We can be very much sure on this case. Therefore, we can switch them back. We then perform the same analysis again.
replace measwt=57 if subject==12
(1 real change made)
replace measht=166 if subject==12
(1 real change made)
list subject measwt measht reptwt reptht in 12/12
subject measwt measht reptwt reptht
12. 59 75 172 70 169
regress measwt measht reptwt reptht
Source | SS df MS Number of obs = 181
---------+------------------------------ F( 3, 177) = 2085.02
Model | 31551.0849 3 10517.0283 Prob > F = 0.0000
Residual | 892.804651 177 5.04409407 R-squared = 0.9725
---------+------------------------------ Adj R-squared = 0.9720
Total | 32443.8895 180 180.243831 Root MSE = 2.2459
------------------------------------------------------------------------------
measwt | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
measht | -.0364477 .088613 -0.411 0.681 -.2113216 .1384262
reptwt | .963793 .0194467 49.561 0.000 .9254157 1.00217
reptht | .0225427 .0811435 0.278 0.781 -.1375904 .1826759
_cons | 4.821849 4.242671 1.137 0.257 -3.550881 13.19458
------------------------------------------------------------------------------
We now see that both measured height and reported height are no longer significant predictors. This is because that the predictors are collinear to each other since we have corrected the entry error. Let’s do another regression with only reported weight as a single predictor. Notice that adjusted R-square is actually the highest among all the regression analysis we have done so far. This shows that data entry error could really distort the regression analysis sometimes.
regress measwt reptwt Source | SS df MS Number of obs = 181 ---------+------------------------------ F( 1, 179) = 6315.72 Model | 31549.7087 1 31549.7087 Prob > F = 0.0000 Residual | 894.180797 179 4.99542345 R-squared = 0.9724 ---------+------------------------------ Adj R-squared = 0.9723 Total | 32443.8895 180 180.243831 Root MSE = 2.235 ------------------------------------------------------------------------------ measwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- reptwt | .9569886 .0120419 79.472 0.000 .9332262 .9807509 _cons | 2.847071 .8081664 3.523 0.001 1.252311 4.44183 ------------------------------------------------------------------------------
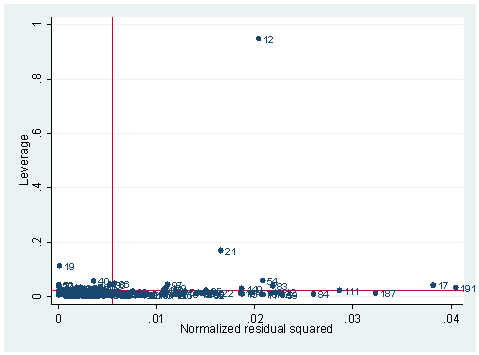
2. Continue with the first model we run in our last exercise. What measure and its corresponding STATA command would you use if you want to know how much change an observation would make on a predictor? For example, how much change would it be for the coefficient of predictor reptht if we omit observation 12 from our regression analysis? What are the other measures that you would use to assess the strength of an observation on regression? What are the commonly suggested cut-off values for them?
Answer: The measure that measures how much impact each observation has on a particular predictor is DFBETAs. The DFBETA for a predictor and for a particular observation is the difference between the regression coefficient calculated for all of the data and the regression coefficient calculated with the observation deleted, scaled by the standard error calculated with the observation deleted. The cut-off value for DFBETAs is 2/sqrt(n), where n is the number of observations. In our case, it will be the absolute value of DFBETAs greater than 2/sqrt(181)=.14866. From our list below, we can see we have several troublesome points with observation 12 the most troublesome one. For observation 12, the DFreptht is 24.25463. That means that including observation 12 in the regression, the regression coefficient for reptht will increase by about 24 times the standard error than the case with the observation excluded.
dfbeta DFmeasht: DFbeta(measht) DFreptwt: DFbeta(reptwt) DFreptht: DFbeta(reptht) hilo DFreptht measwt measht reptwt reptht subject, show(5) 5 lowest and highest observations on DFreptht DFreptht measwt measht reptwt reptht subject -.3410896 53 169 52 175 83 -.2115161 88 185 93 188 191 -.1834869 59 182 61 183 86 -.1629187 65 187 67 188 40 -.1510676 79 179 79 171 112 DFreptht measwt measht reptwt reptht subject 0904913 63 160 64 158 78 1255461 69 167 73 165 122 1791834 85 191 83 188 140 4119168 119 180 124 178 21 24.25463 166 57 56 163 12
DFBETAs are calculation intensive as it is for computed each predictor and each observation. DFITS and Cook’s D, on the other hand, are summary information of the influence (leverage and residual) and are much less computation intensive. For example, we can look at DFITS after the regression, similar to what we did in Exercise 1. The cut-off values of DFITS and Cook’s D is 2*sqrt(k/n) and 4/n respectively. Observations with DFITS or Cook’s D value greater than these cut-off values deserve further investigation.
3. The following data file is called bbwt.dta and it is from Weisberg’s Applied Regression Analysis. It consists of the body weights and brain weight of some 60 animals. We want to predict the brain weight by body weight, that is, a simple linear regression of brain weight against body weight. Show what you have to do to verify the linearity assumption. If you think that it violates the linearity assumption, show some possible remedies that you would consider.
use bbwt, clearregress brainwt bodywtSource | SS df MS Number of obs = 62 ---------+------------------------------ F( 1, 60) = 411.12 Model | 46067326.8 1 46067326.8 Prob > F = 0.0000 Residual | 6723217.18 60 112053.62 R-squared = 0.8726 ---------+------------------------------ Adj R-squared = 0.8705 Total | 52790543.9 61 865418.753 Root MSE = 334.74 ------------------------------------------------------------------------------ brainwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- bodywt | .9664599 .0476651 20.276 0.000 .8711155 1.061804 _cons | 91.00865 43.55574 2.089 0.041 3.884201 178.1331 ------------------------------------------------------------------------------
Answer: In general, we can use acprplot to verify the linearity assumption against a predictor. For example, we can do after the regression above the acprplot against our only predictor bodywt.
acprplot bodywt, mspline
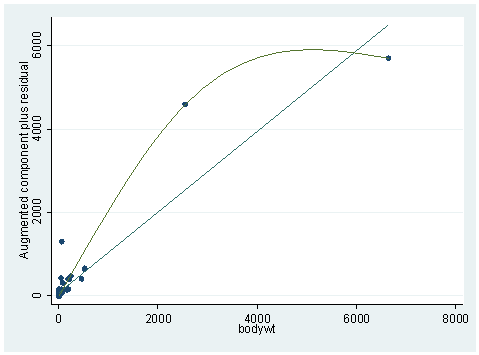
The graph does not look very linear. In our chapter, we did some logarithm transformations. We’ll try it here and the results are shown below. Notice the plot is much nicer this time. The adjusted R-square is also up by .05.
gen lbdwt=log(bodywt) gen lbrwt=log(brainwt) regress lbrwt lbdwt Source | SS df MS Number of obs = 62 ---------+------------------------------ F( 1, 60) = 697.42 Model | 336.188605 1 336.188605 Prob > F = 0.0000 Residual | 28.9226087 60 .482043478 R-squared = 0.9208 ---------+------------------------------ Adj R-squared = 0.9195 Total | 365.111213 61 5.98542973 Root MSE = .69429 ------------------------------------------------------------------------------ lbrwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- lbdwt | .7516861 .0284635 26.409 0.000 .6947507 .8086216 _cons | 2.134788 .0960432 22.227 0.000 1.942673 2.326903 ------------------------------------------------------------------------------ acprplot lbdwt, mspline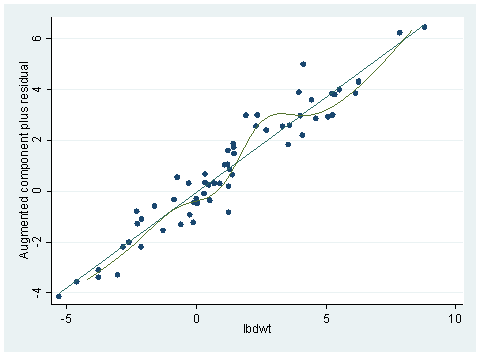
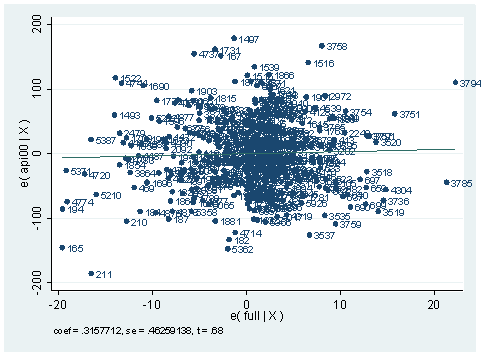
4. We did a regression analysis using data file elemapi in chapter 2. Continuing with the analysis we did, we did an avplot here. Explain what an avplot is and how you would interpret the avplot below. If full were put in the model, would it be a significant predictor?
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear regress api00 meals ell emerSource | SS df MS Number of obs = 400 ---------+------------------------------ F( 3, 396) = 673.00 Model | 6749782.75 3 2249927.58 Prob > F = 0.0000 Residual | 1323889.25 396 3343.15467 R-squared = 0.8360 ---------+------------------------------ Adj R-squared = 0.8348 Total | 8073672.00 399 20234.7669 Root MSE = 57.82 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- meals | -3.159189 .1497371 -21.098 0.000 -3.453568 -2.864809 ell | -.9098732 .1846442 -4.928 0.000 -1.272878 -.5468678 emer | -1.573496 .293112 -5.368 0.000 -2.149746 -.9972456 _cons | 886.7033 6.25976 141.651 0.000 874.3967 899.0098 ------------------------------------------------------------------------------avplot full, mlabel(snum)
Answer: A group of points can be jointly influential. An avplot is an attractive graphic method to present multiple influential points on a predictor. What we are looking for in an avplot are those points that can exert substantial change to the regression line. For example, in the plot above, the observation with school number 211 is very low at the left corner of the plot. Deleting it would flatten the regression line a lot, in other words, it would decrease the regression coefficient for variable full significantly. You can compare the regression that includes the variable full and the entire data set and the model without the observation with snum 211.
regress api00 meals ell emer full
Source | SS df MS Number of obs = 400
---------+------------------------------ F( 4, 395) = 504.18
Model | 6751342.63 4 1687835.66 Prob > F = 0.0000
Residual | 1322329.37 395 3347.66928 R-squared = 0.8362
---------+------------------------------ Adj R-squared = 0.8346
Total | 8073672.00 399 20234.7669 Root MSE = 57.859
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
meals | -3.156558 .1498877 -21.059 0.000 -3.451236 -2.861881
ell | -.8981675 .1855628 -4.840 0.000 -1.262982 -.5333532
emer | -1.225015 .58877 -2.081 0.038 -2.38253 -.0675008
full | .3157712 .4625914 0.683 0.495 -.5936778 1.22522
_cons | 855.0671 46.76702 18.284 0.000 763.1237 947.0105
------------------------------------------------------------------------------
regress api00 meals ell emer full if snum !=211
Source | SS df MS Number of obs = 399
---------+------------------------------ F( 4, 394) = 513.16
Model | 6715948.02 4 1678987.01 Prob > F = 0.0000
Residual | 1289106.10 394 3271.84289 R-squared = 0.8390
---------+------------------------------ Adj R-squared = 0.8373
Total | 8005054.12 398 20113.2013 Root MSE = 57.20
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
meals | -3.164431 .1482011 -21.352 0.000 -3.455795 -2.873067
ell | -.8930366 .1834563 -4.868 0.000 -1.253712 -.5323609
emer | -1.411583 .585001 -2.413 0.016 -2.561697 -.2614692
full | .1213333 .4613751 0.263 0.793 -.7857315 1.028398
_cons | 874.6425 46.64066 18.753 0.000 782.9468 966.3382
------------------------------------------------------------------------------
Of course, there are other points that are in similar nature as the observation with snum 211 shown in the avplot that are worth paying more attention to. On the other hand, if we look at the t-value on top of the avplot, it is only 68. The p-value corresponding to it will be the probability for t-distribution with degree of freedom being the total degree of freedom. :
di tprob(399, .683) 49500322
which is not significant. The equation on top of the avplot is actually the regression coefficient and its standard error if the variable were a predictor. In our regression which includes full and all the data, we see that coefficient for full is .3157712 and the standard error for it is .4625914. They are exactly the same as shown on top of the avplot.
5. The data set wage.dta is from a national sample of 6000 households with a male head earning less than $15,000 annually in 1966. The data were classified into 39 demographic groups for analysis. We tried to predict the average hours worked by average age of respondent and average yearly non-earned income.
use wage, clear regress HRS AGE NEINSource | SS df MS Number of obs = 39 ---------+------------------------------ F( 2, 36) = 39.72 Model | 107205.109 2 53602.5543 Prob > F = 0.0000 Residual | 48578.1222 36 1349.39228 R-squared = 0.6882 ---------+------------------------------ Adj R-squared = 0.6708 Total | 155783.231 38 4099.5587 Root MSE = 36.734 ------------------------------------------------------------------------------ HRS | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- AGE | -8.281632 1.603736 -5.164 0.000 -11.53416 -5.029104 NEIN | .4289202 .0484882 8.846 0.000 .3305816 .5272588 _cons | 2321.03 57.55038 40.330 0.000 2204.312 2437.748 ------------------------------------------------------------------------------
Both predictors are significant. Now if we add ASSET to our predictors list, neither NEIN nor ASSET is significant.
regress HRS AGE NEIN ASSETSource | SS df MS Number of obs = 39 ---------+------------------------------ F( 3, 35) = 25.83 Model | 107317.64 3 35772.5467 Prob > F = 0.0000 Residual | 48465.5908 35 1384.73117 R-squared = 0.6889 ---------+------------------------------ Adj R-squared = 0.6622 Total | 155783.231 38 4099.5587 Root MSE = 37.212 ------------------------------------------------------------------------------ HRS | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- AGE | -8.007181 1.88844 -4.240 0.000 -11.84092 -4.173443 NEIN | .3338277 .337171 0.990 0.329 -.3506658 1.018321 ASSET | .0044232 .015516 0.285 0.777 -.027076 .0359223 _cons | 2314.054 63.22636 36.600 0.000 2185.698 2442.411 ------------------------------------------------------------------------------
Can you explain why?
Answer: If we look at our data set more carefully, for example, we can do a describe at the beginning of regression analysis, we would notice that variable NEIN and ASSET are very closed related. Therefore, we would expect that these two variables are strongly correlated. We can also do a scatter plot to check on this. Here is what we have done:
describe NEIN ASSETstorage display value variable name type format label variable label ------------------------------------------------------------------------------- NEIN float %9.0g Average yearly non-earned income ASSET float %9.0g Average family asset holdings (Bank account, etc.) ($)twoway (scatter NEIN ASSET) (lfit NEIN ASSET)
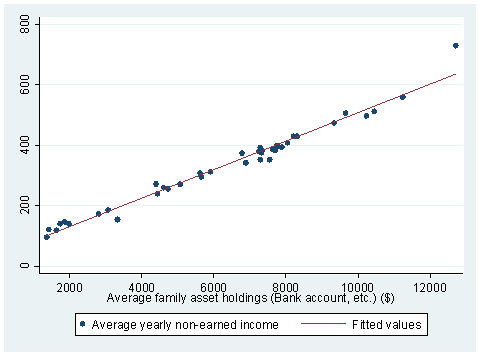
Another useful command introduced in this chapter is vif.
regress HRS AGE NEIN
(Output is shown above.)
vif
Variable | VIF 1/VIF
---------+----------------------
AGE | 1.29 0.774467
NEIN | 1.29 0.774467
---------+----------------------
Mean VIF | 1.29
regress HRS AGE NEIN ASSET
(Output is shown above.)
vif
Variable | VIF 1/VIF
---------+----------------------
NEIN | 60.84 0.016436
ASSET | 56.07 0.017836
AGE | 1.74 0.573178
---------+----------------------
Mean VIF | 39.55
So we see that in the first regression, there is no evidence of collinearity since the variance inflation factors are fairly small. But in the second regression analysis, the vif for NEIN and ASSET jumped up to around 60, which indicates strongly the appearance of collinearity among the predictors. The collinearity can also be detected by using the command collin.
collin NEIN ASSET AGE
Collinearity Diagnostics
SQRT Cond
Variable VIF VIF Tolerance Eigenval Index
-------------------------------------------------------------
NEIN 60.84 7.80 0.0164 2.2855 1.0000
ASSET 56.07 7.49 0.0178 0.7059 1.7994
AGE 1.74 1.32 0.5732 0.0086 16.3386
-------------------------------------------------------------
Mean VIF 39.55 Condition Number 16.3386
6. Continue to use the previous data set. This time we want to predict the average hourly wage by the average percent of white respondents. Carry out the regression analysis and list the STATA commands that you can use to check for heteroscedasticity. Explain the results of the test(s).
use wage, clear regress RATE RACE Source | SS df MS Number of obs = 31 ---------+------------------------------ F( 1, 29) = 22.82 Model | 2.16442894 1 2.16442894 Prob > F = 0.0000 Residual | 2.75013286 29 .094832168 R-squared = 0.4404 ---------+------------------------------ Adj R-squared = 0.4211 Total | 4.91456181 30 .163818727 Root MSE = .30795 ------------------------------------------------------------------------------ RATE | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- RACE | -.0142697 .0029869 -4.777 0.000 -.0203786 -.0081608 _cons | 3.367147 .1261571 26.690 0.000 3.109127 3.625168 ------------------------------------------------------------------------------ hettest Cook-Weisberg test for heteroscedasticity using fitted values of RATE Ho: Constant variance chi2(1) = 0.42 Prob > chi2 = 0.5186 whitetst (8 missing values generated) (8 missing values generated) White's general test statistic : .5617374 Chi-sq( 2) P-value = .7551rvfplot
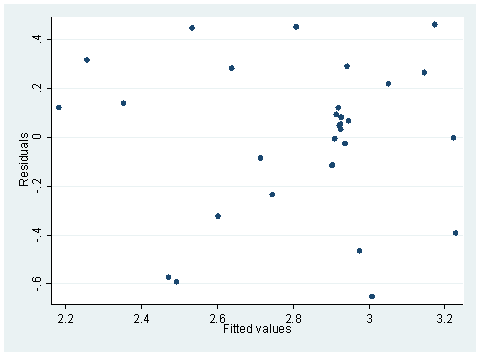
The hettest and whitetst are based on the null hypothesis that the variance is constant. Therefore, when the probability is large, we will accept the null hypothesis of constant variance. The rvfplot also shows that the variance across fitted values does not change a lot, as overall speaking we see a band of equal width. On the other hand, the regression below is different. Both hettest and whitetst are significant, indicating heteroscedasticity. This can also be seen from the rvfplot below, we see that the band is getting wider to the right.
regress RACE HRS Source | SS df MS Number of obs = 31 ---------+------------------------------ F( 1, 29) = 65.14 Model | 7355.07438 1 7355.07438 Prob > F = 0.0000 Residual | 3274.4589 29 112.912376 R-squared = 0.6919 ---------+------------------------------ Adj R-squared = 0.6813 Total | 10629.5333 30 354.317776 Root MSE = 10.626 ------------------------------------------------------------------------------ RACE | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- HRS | -.2801356 .0347093 -8.071 0.000 -.351124 -.2091472 _cons | 639.3401 74.53629 8.578 0.000 486.8963 791.7839 ------------------------------------------------------------------------------ hettest Cook-Weisberg test for heteroscedasticity using fitted values of RACE Ho: Constant variance chi2(1) = 6.60 Prob > chi2 = 0.0102 whitetst White's general test statistic : 7.889606 Chi-sq( 2) P-value = .0194 rvfplot
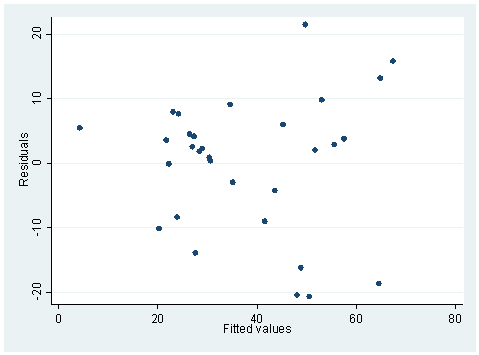
7. We have a data set that consists of volume, diameter and height of some objects. Someone did a regression of volume on diameter and height.
use tree, clear regress vol dia heightSource | SS df MS Number of obs = 31 ---------+------------------------------ F( 2, 28) = 254.97 Model | 7684.16254 2 3842.08127 Prob > F = 0.0000 Residual | 421.921306 28 15.0686181 R-squared = 0.9480 ---------+------------------------------ Adj R-squared = 0.9442 Total | 8106.08385 30 270.202795 Root MSE = 3.8818 ------------------------------------------------------------------------------ vol | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- dia | 4.708161 .2642646 17.816 0.000 4.166839 5.249482 height | .3392513 .1301512 2.607 0.014 .0726487 .6058538 _cons | -57.98766 8.638225 -6.713 0.000 -75.68226 -40.29306 ------------------------------------------------------------------------------
Explain what tests you can use to detect model specification errors and if there is any, your solution to correct it.
Answer: We can use linktest and ovtest to detect model specification errors.
linktest
Source | SS df MS Number of obs = 31
---------+------------------------------ F( 2, 28) = 594.19
Model | 7919.48998 2 3959.74499 Prob > F = 0.0000
Residual | 186.593864 28 6.66406657 R-squared = 0.9770
---------+------------------------------ Adj R-squared = 0.9753
Total | 8106.08385 30 270.202795 Root MSE = 2.5815
------------------------------------------------------------------------------
vol | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
_hat | .3606632 .1115454 3.233 0.003 .1321728 .5891537
_hatsq | .0094227 .0015856 5.942 0.000 .0061746 .0126707
_cons | 8.376438 1.729554 4.843 0.000 4.833608 11.91927
------------------------------------------------------------------------------
ovtest
Ramsey RESET test using powers of the fitted values of vol
Ho: model has no omitted variables
F(3, 25) = 11.54
Prob > F = 0.0001
For linktest we look for p-value for the square term and both the linktest and ovtest are significant indicating that our model is not specified correctly. It is actually easy to understand in this case, since we look for the relationship between volume, which is 3-dimensional and diameter and height, which are 1-dimensional. So it is reasonable to put in higher degree terms. One solution is to put the squared diameter term into our regression as shown below. Both the linktest and ovtest are no longer significant.
gen dia2=dia*dia regress vol dia dia2 height Source | SS df MS Number of obs = 31 ---------+------------------------------ F( 3, 27) = 383.20 Model | 7920.07197 3 2640.02399 Prob > F = 0.0000 Residual | 186.011883 27 6.889329 R-squared = 0.9771 ---------+------------------------------ Adj R-squared = 0.9745 Total | 8106.08385 30 270.202795 Root MSE = 2.6248 ------------------------------------------------------------------------------ vol | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- dia | -2.885077 1.309851 -2.203 0.036 -5.572669 -.1974846 dia2 | .2686224 .0459048 5.852 0.000 .1744335 .3628112 height | .3763873 .088232 4.266 0.000 .1953502 .5574244 _cons | -9.920417 10.07912 -0.984 0.334 -30.60105 10.76022 ------------------------------------------------------------------------------linktest Source | SS df MS Number of obs = 31 ---------+------------------------------ F( 2, 28) = 596.13 Model | 7920.08338 2 3960.04169 Prob > F = 0.0000 Residual | 186.00047 28 6.64287391 R-squared = 0.9771 ---------+------------------------------ Adj R-squared = 0.9754 Total | 8106.08385 30 270.202795 Root MSE = 2.5774 ------------------------------------------------------------------------------ vol | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- _hat | 1.004811 .1199563 8.376 0.000 .7590915 1.25053 _hatsq | -.0000621 .0015027 -0.041 0.967 -.0031403 .0030161 _cons | -.0727509 2.019028 -0.036 0.972 -4.208542 4.06304 ------------------------------------------------------------------------------ ovtest Ramsey RESET test using powers of the fitted values of vol Ho: model has no omitted variables F(3, 24) = 0.43 Prob > F = 0.7312