1. Using the elemapi2 data file ( use https://stats.idre.ucla.edu/stat/stata/examples/ara/elemapi2 ) convert the variable ell into 2 categories using the following coding, 0-25 on ell becomes 0, and 26-100 on ell becomes 1. Use this recoded version of ell to predict api00 and interpret the results.
Answer 1.
We first use the elemapi2 data file
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear
We convert ell into a 0/1 variable called ell_bin.
gen ell_bin = ell recode ell_bin 0/25 = 0 26/100=1 (398 changes made)
We tabulate ell_bin to see that the recoding looks OK.
tab ell_bin
ell_bin | Freq. Percent Cum.
------------+-----------------------------------
0 | 201 50.25 50.25
1 | 199 49.75 100.00
------------+-----------------------------------
Total | 400 100.00
We now include ell_bin in the regression model.
regress api00 ell_bin
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 1, 398) = 451.15
Model | 4289511.71 1 4289511.71 Prob > F = 0.0000
Residual | 3784160.29 398 9507.94043 R-squared = 0.5313
-------------+------------------------------ Adj R-squared = 0.5301
Total | 8073672.00 399 20234.7669 Root MSE = 97.509
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ell_bin | -207.114 9.750989 -21.24 0.000 -226.2838 -187.9441
_cons | 750.6617 6.877731 109.14 0.000 737.1405 764.1829
------------------------------------------------------------------------------
The coefficient for _cons represents the api scores for the schools where ell_bin is coded 0 (low number of English language learners). The coefficient for ell_bin represents the api scores for the schools with a high number of English language learners minus the api scores for the api scores for the schools with a low number of English language learners. When broken into these two categories, the schools with the high number of English language learners score 207 points lower on the api scores than schools with a low number of English language learners.
2. Convert the variable ell into 3 categories coding those scoring 0-14 on ell as 1, and those 15/41 as 2 and 42/100 as 3. Do an analysis predicting api00 from the ell variable converted to a 1/2/3 variable. Interpret the results.
Answer 2.
First we create the categorical variable called ell_cat.
generate ell_cat = ell recode ell_cat 0/14=1 15/41=2 42/100=3 (385 changes made)
We check the creation of ell_cat using the tabulate command below.
tabulate ell_cat
ell_cat | Freq. Percent Cum.
------------+-----------------------------------
1 | 136 34.00 34.00
2 | 129 32.25 66.25
3 | 135 33.75 100.00
------------+-----------------------------------
Total | 400 100.00
We use xi with the regress command to perform this analysis, and this creates two dummy codes with category 1 (low number of English language learners) as the reference category.
xi : regress api00 i.ell_cat
i.ell_cat _Iell_cat_1-3 (naturally coded; _Iell_cat_1 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 252.88
Model | 4523139.17 2 2261569.59 Prob > F = 0.0000
Residual | 3550532.82 397 8943.40762 R-squared = 0.5602
-------------+------------------------------ Adj R-squared = 0.5580
Total | 8073672.00 399 20234.7669 Root MSE = 94.57
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iell_cat_2 | -141.319 11.62278 -12.16 0.000 -164.1689 -118.4691
_Iell_cat_3 | -257.9758 11.48947 -22.45 0.000 -280.5636 -235.388
_cons | 780.2647 8.109276 96.22 0.000 764.3222 796.2072
------------------------------------------------------------------------------
The _cons represents the mean for the reference category, when ell_cat is coded 1. The coefficient for _Iell_cat_2 is the difference in the mean api score between the ell_cat=2 group and the reference group, ell_cat=1, and this difference is significant. The schools with a middle amount of English language learners score 141 points lower on their api score as compared to the schools with low amounts of English language learners. The coefficient for _Iell_cat_3 is the difference in the api scores for the ell_cat=3 group and the reference group, and this is significant as well. The schools with high amounts of English language learners score about 257 points lower than schools with low amounts of English language learners.
3. Do a regression analysis predicting api00 from yr_rnd and the ell variable converted to a 0/1 variable. Then create an interaction term and run the analysis again. Interpret the results of these analyses.
Answer 3.
We use the regress command to perform this analysis below.
regress api00 yr_rnd ell_bin
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 270.17
Model | 4654146.48 2 2327073.24 Prob > F = 0.0000
Residual | 3419525.51 397 8613.41439 R-squared = 0.5765
-------------+------------------------------ Adj R-squared = 0.5743
Total | 8073672.00 399 20234.7669 Root MSE = 92.808
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd | -77.6647 11.93665 -6.51 0.000 -101.1316 -54.19776
ell_bin | -182.082 10.04678 -18.12 0.000 -201.8335 -162.3304
_cons | 756.0712 6.598791 114.58 0.000 743.0982 769.0441
------------------------------------------------------------------------------
These results indicate that year round schools (yr_rnd=1) score about 77 points lower on the api test than non-year round schools (yr_rnd=0). Also, schools with high numbers of English language learners score about 182 points lower on the api test than the schools with low numbers of English language learners. Both of these effects are significant.
Now we include an interaction term in the analysis.
generate yr_ell = yr_rnd*ell_bin regress api00 yr_rnd ell_bin yr_ell
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 179.67
Model | 4654224.91 3 1551408.30 Prob > F = 0.0000
Residual | 3419447.09 396 8634.96739 R-squared = 0.5765
-------------+------------------------------ Adj R-squared = 0.5733
Total | 8073672.00 399 20234.7669 Root MSE = 92.925
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd | -75.49121 25.748 -2.93 0.004 -126.1111 -24.87135
ell_bin | -181.6966 10.84157 -16.76 0.000 -203.0109 -160.3824
yr_ell | -2.770387 29.06936 -0.10 0.924 -59.91995 54.37918
_cons | 755.9198 6.795314 111.24 0.000 742.5604 769.2792
------------------------------------------------------------------------------
The main effects of yr_rnd and ell_bin are still significant, but the interaction term yr_ell is not significant. This suggests that the effects we described in the analysis above are consistent across the levels of yr_rnd and ell_bin. In other words, we can say that the effect of ell_bin is much the same for the year round schools as for the non-year round schools.
We could also have run this analysis using the anova command, which can be much more convenient for models like these.
anova api00 yr_rnd ell_bin yr_rnd*ell_bin
Number of obs = 400 R-squared = 0.5765
Root MSE = 92.9245 Adj R-squared = 0.5733
Source | Partial SS df MS F Prob > F
---------------+----------------------------------------------------
Model | 4654224.91 3 1551408.30 179.67 0.0000
|
yr_rnd | 241566.044 1 241566.044 27.98 0.0000
ell_bin | 1370062.10 1 1370062.10 158.66 0.0000
yr_rnd*ell_bin | 78.4279246 1 78.4279246 0.01 0.9241
|
Residual | 3419447.09 396 8634.96739
---------------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
And we can use the adjust command to get the means for the cells. You can relate the coefficients from the regression model to the means below. For example, the _cons is the mean for the cell where all the variables are 0, and so forth.
adjust , by(yr_rnd ell_bin)
-----------------------------------------------------
Dependent variable: api00 Command: anova
-----------------------------------------------------
----------------------------
year |
round | ell_bin
school | 0 1
----------+-----------------
No | 755.92 574.223
Yes | 680.429 495.962
----------------------------
Key: Linear Prediction
4. Do a regression analysis predicting api00 from ell coded as 0/1 (from question 1) and some_col, and the interaction of these two variables. Interpret the results, including showing a graph of the results.
Answer 4.
Create an interaction and run the analysis
gen ell_col = ell_bin*some_col regress api00 ell_bin some_col ell_col
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 167.96
Model | 4520787.76 3 1506929.25 Prob > F = 0.0000
Residual | 3552884.24 396 8971.9299 R-squared = 0.5599
-------------+------------------------------ Adj R-squared = 0.5566
Total | 8073672.00 399 20234.7669 Root MSE = 94.72
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ell_bin | -291.6353 19.90341 -14.65 0.000 -330.7649 -252.5057
some_col | -1.443942 .5595276 -2.58 0.010 -2.543958 -.3439265
ell_col | 4.622981 .9174408 5.04 0.000 2.819317 6.426644
_cons | 784.5261 14.72533 53.28 0.000 755.5765 813.4757
------------------------------------------------------------------------------
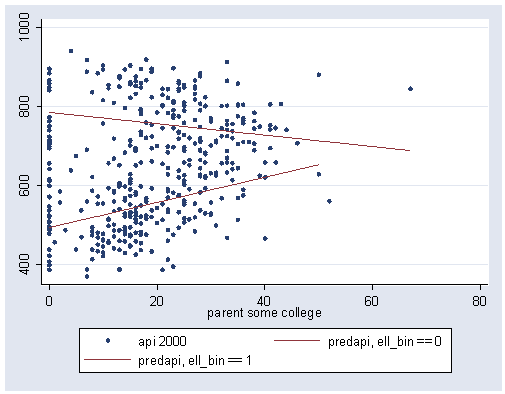
Make a graph to help in the interpretation.
predict predapi
separate predapi, by(ell_bin)
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------
predapi0 float %9.0g predapi, ell_bin == 0
predapi1 float %9.0g predapi, ell_bin == 1
graph twoway scatter api00 predapi0 predapi1 some_col, /// connect(i l l i) msymbol(o i i o) pstyle(p1 p2 p2 p1) sort
The graph helps us visually understand the interaction represented by ell_col. We can see that the regression lines between some_col and api00 are not parallel — specifically, the line for the schools with a low number of English language learners has a downward slope, and the line for the schools with a large number of English language learners has an upward slope. From the regression equation, we see that the slope of the line when ell_bin is 0 (low number of English language learners) is -1.44. This corresponds to the solid regression line we see in the above graph. The difference between the slopes for the schools with a high number of English language learners and the schools with a low number of English language learners is 4.62. In order to get the slopes for the schools with a high number of English language learners we would add 4.62 to -1.44 and that yields 3.18, so this is the slope for the line for the schools with the high number of English language learners. This corresponds to the dotted regression line that we see in the above graph.
5. Use the variable ell converted into 3 categories (from question 2) and predict api00 from ell in 3 categories, from some_col and the interaction. of these two variables. Interpret the results, including showing a graph.
We use the xi command with regress to perform the analysis looking at the effect of some_col and ell_cat and the interaction.
xi : regress api00 i.ell_cat*some_col
i.ell_cat _Iell_cat_1-3 (naturally coded; _Iell_cat_1 omitted)
i.ell_~t*some~l _IellXsome__# (coded as above)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 109.56
Model | 4696120.14 5 939224.028 Prob > F = 0.0000
Residual | 3377551.86 394 8572.46664 R-squared = 0.5817
-------------+------------------------------ Adj R-squared = 0.5763
Total | 8073672.00 399 20234.7669 Root MSE = 92.588
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iell_cat_2 | -199.7005 25.2889 -7.90 0.000 -249.4186 -149.9825
_Iell_cat_3 | -349.7611 23.60764 -14.82 0.000 -396.1738 -303.3484
some_col | -2.056112 .6695881 -3.07 0.002 -3.372524 -.7396998
_IellXsome~2 | 2.48773 1.003112 2.48 0.014 .5156074 4.459852
_IellXsome~3 | 5.112258 1.159782 4.41 0.000 2.832123 7.392393
_cons | 829.4451 17.87578 46.40 0.000 794.3012 864.5889
------------------------------------------------------------------------------
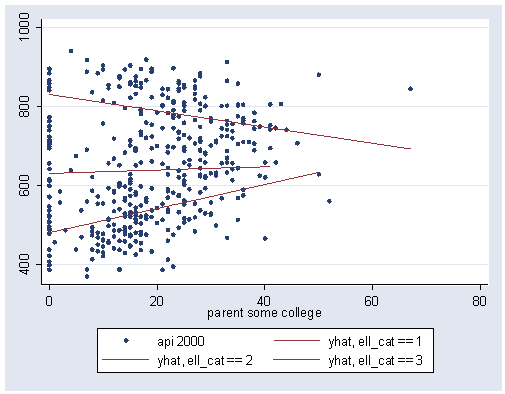
To help interpretation, lets make a graph of the predicted values.
predict yhat
(option xb assumed; fitted values)
separate yhat, by(ell_cat)
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------
yhat1 float %9.0g yhat, ell_cat == 1
yhat2 float %9.0g yhat, ell_cat == 2
yhat3 float %9.0g yhat, ell_cat == 3
graph twoway scatter api00 yhat1 yhat2 yhat3 some_col, /// connect(i l l l i) msymbol(o i i i o) pstyle(p1 p2 p2 p2 p1) sort
We can use the information in the graph and in the regression equation to help interpret these results. First looking at the graph, we see that the slopes of the three regression lines are not parallel. For the schools with a low number of English language learners (when ell_cat is 1) the regression line has a downward slope, for the schools with a middle number of English language learners (when ell_cat is 2) the regression line is pretty flat, and for the schools with a high number of English language learners (when ell_cat is 3) the regression line has an upward tilt. we can use the regression model to compute the exact slopes of all three of these regression lines. Since group 1 is the reference category the slope for that regression line is the slope for some_col, which is -2.05.
The coefficient for _IellXsome~2 (2.48) tells us how much we need to add to -2.05 to get the coefficient for the second group. when we add -2.05 to 2.48 we get .43, the slope for the second group. Because the coefficient _IellXsome~2 is significant we can say that the coefficient for group 1 is significantly different from group 2.
The coefficient for _IellXsome~3 (5.11) tells us how much we need to add to -2.05 to get the coefficient for the third group. when we add -2.05 to 5.11 we get 3.06, the slope for the third group. Because the coefficient _IellXsome~3 is significant we can say that the coefficient for group 1 is significantly different from group 3.