1. Use the crime data file that was used in chapter 2 (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/crime ) and look at a regression model predicting murder from pctmetro, poverty, pcths and single using OLS and make a avplots and a lvr2plot following the regression. Are there any states that look worrisome? Repeat this analysis using regression with robust standard errors and show avplots for the analysis. Repeat the analysis using robust regression and make a manually created lvr2plot. Also run the results using qreg. Compare the results of the different analyses. Look at the weights from the robust regression and comment on the weights.
Answer 1.
First, consider the OLS regression predicting murder from pctmetro,
poverty, pcths and single.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/crime , clear
(crime data from agresti & finlay - 1997)
regress murder pctmetro poverty pcths single
Source | SS df MS Number of obs = 51
-------------+------------------------------ F( 4, 46) = 37.90
Model | 4406.42207 4 1101.60552 Prob > F = 0.0000
Residual | 1336.89947 46 29.0630319 R-squared = 0.7672
-------------+------------------------------ Adj R-squared = 0.7470
Total | 5743.32154 50 114.866431 Root MSE = 5.391
------------------------------------------------------------------------------
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0682218 .0380637 1.79 0.080 -.0083964 .14484
poverty | .4380115 .3259862 1.34 0.186 -.2181648 1.094188
pcths | .0243003 .2220237 0.11 0.913 -.4226102 .4712109
single | 3.650532 .4982054 7.33 0.000 2.647697 4.653367
_cons | -45.31188 19.39747 -2.34 0.024 -84.35697 -6.266792
------------------------------------------------------------------------------
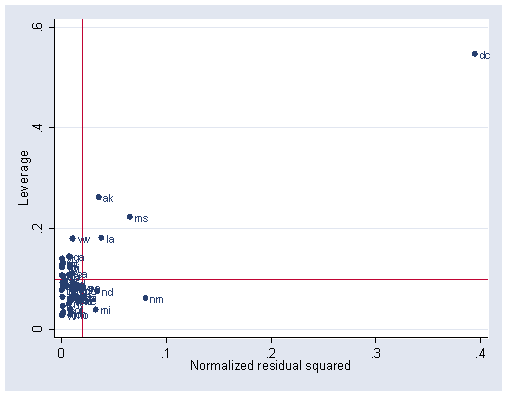
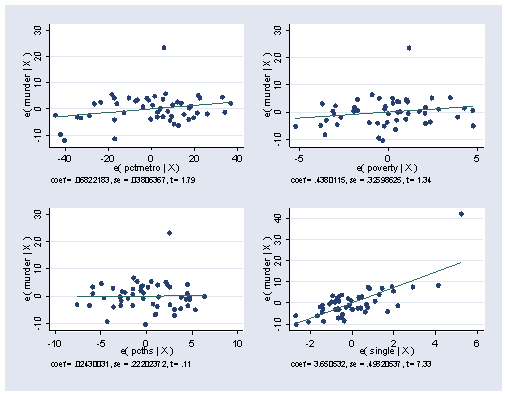
These results suggest that single is the only predictor significantly related to number of murders in a state. Let’s look at the lvr2plot for this analysis. Washington DC looks like it has both a very high leverage and a very high residual.
. lvr2plot, mlabel(state)
. avplots
Let’s consider the same analysis using robust standard errors. The results are largely the same, except that the p value for pctmetro fell from 0.08 to 0.049, which would then make it a significant predictor, however we would be somewhat skeptical of this particular result without further investigation.
regress murder pctmetro poverty pcths single, robust
Regression with robust standard errors Number of obs = 51
F( 4, 46) = 7.20
Prob > F = 0.0001
R-squared = 0.7672
Root MSE = 5.391
------------------------------------------------------------------------------
| Robust
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0682218 .0337517 2.02 0.049 .0002832 .1361604
poverty | .4380115 .2568971 1.71 0.095 -.0790955 .9551185
pcths | .0243003 .1841403 0.13 0.896 -.3463549 .3949556
single | 3.650532 1.152474 3.17 0.003 1.330723 5.970341
_cons | -45.31188 25.39531 -1.78 0.081 -96.42999 5.806231
------------------------------------------------------------------------------
Stata allows us to compute the residual for this analysis but will not allow us to compute the leverage (hat) value. So instead of showing a lvr2plot let’s look at the avplots for this analysis.
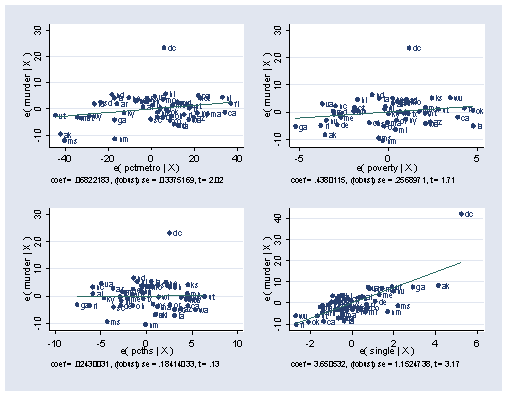
. avplots , mlabel(state)
As you can see, we still have an observation that sticks out from the rest, and this is Washington DC. This is especially pronounced for the lower right graph for single where DC would seem to have very strong leverage to influence the coefficient for single.
Now, let’s look at the analysis using robust regression and save the weights, calling them rrwt.
rreg murder pctmetro poverty pcths single, genwt(rrwt)
Huber iteration 1: maximum difference in weights = .44857261
Huber iteration 2: maximum difference in weights = .0399983
Biweight iteration 3: maximum difference in weights = .15321379
Biweight iteration 4: maximum difference in weights = .00973214
Robust regression estimates Number of obs = 50
F( 4, 45) = 35.25
Prob > F = 0.0000
------------------------------------------------------------------------------
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0535439 .0146555 3.65 0.001 .0240262 .0830615
poverty | .182561 .1259505 1.45 0.154 -.0711163 .4362383
pcths | -.2245853 .0863452 -2.60 0.013 -.3984936 -.0506771
single | 1.392942 .2355845 5.91 0.000 .9184503 1.867434
_cons | 2.888033 7.945302 0.36 0.718 -13.11463 18.89069
------------------------------------------------------------------------------
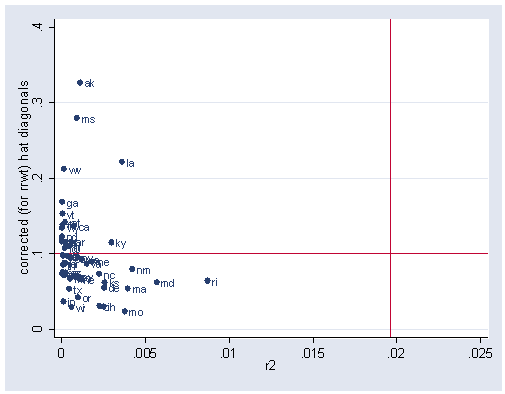
If you try the avplots command, this command is not available after rreg and the lvr2plot is not available either. But we can manually create the residual and hat values and create an lvr2plot of our own, see below.
predict r, r predict h, hat generate r2=r^2 sum r2 <output omitted> replace r2 = r2/r(sum) summarize r2 <output omitted> local rm = r(mean) summarize h <output omitted> local hm = r(mean) graph twoway scatter h r2 if state ~= "dc", yline(`hm') xline(`rm') mlabel(state) xlabel(0(.005).025)
As you see above, using the robust regression, none of the observations are jointly high in leverage and their residual values. Let’s recap the regress results and the rreg results below and compare them.
regress murder pctmetro poverty pcths single
Source | SS df MS Number of obs = 51
-------------+------------------------------ F( 4, 46) = 37.90
Model | 4406.42207 4 1101.60552 Prob > F = 0.0000
Residual | 1336.89947 46 29.0630319 R-squared = 0.7672
-------------+------------------------------ Adj R-squared = 0.7470
Total | 5743.32154 50 114.866431 Root MSE = 5.391
------------------------------------------------------------------------------
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0682218 .0380637 1.79 0.080 -.0083964 .14484
poverty | .4380115 .3259862 1.34 0.186 -.2181648 1.094188
pcths | .0243003 .2220237 0.11 0.913 -.4226102 .4712109
single | 3.650532 .4982054 7.33 0.000 2.647697 4.653367
_cons | -45.31188 19.39747 -2.34 0.024 -84.35697 -6.266792
------------------------------------------------------------------------------
rreg murder pctmetro poverty pcths single
Huber iteration 1: maximum difference in weights = .44857261
Huber iteration 2: maximum difference in weights = .0399983
Biweight iteration 3: maximum difference in weights = .15321379
Biweight iteration 4: maximum difference in weights = .00973214
Robust regression estimates Number of obs = 50
F( 4, 45) = 35.25
Prob > F = 0.0000
------------------------------------------------------------------------------
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0535439 .0146555 3.65 0.001 .0240262 .0830615
poverty | .182561 .1259505 1.45 0.154 -.0711163 .4362383
pcths | -.2245853 .0863452 -2.60 0.013 -.3984936 -.0506771
single | 1.392942 .2355845 5.91 0.000 .9184503 1.867434
_cons | 2.888033 7.945302 0.36 0.718 -13.11463 18.89069
------------------------------------------------------------------------------
The results are consistent for poverty and for single, where poverty was not significant in both analyses and single was significant in both analyses. However, the results for pctmetro and pcths were both not significant in the OLS analysis and were significant in the robust regression anlaysis.
Let’s look at the weights used in the robust regression to further understand why the results were so different. Note that the weight for dc is . meaning that it was eliminated from the analysis entirely (because it had such a high residual). Also, ri was weighted by less than half.
hilo rrwt state
10 lowest and highest observations on rrwt
rrwt state
46982663 ri
62949383 md
716977 nm
73472243 ma
74565543 mo
75750112 la
79708217 ky
82324958 ks
82552144 de
82728266 il
rrwt state
99592844 sd
99639177 pa
99799356 fl
99811845 vt
99838103 ga
99863411 nh
99981867 wy
99986937 nd
99991851 ok
dc
In our analyses in chapter 2 (involving different variables) we found dc to be a very serious outlier and decided that it should be excluded because it is not a state. If we investigated further into these variables we may reach the same conclusion and decide that dc should be excluded. If we did, we could try using OLS regression like this. These results are quite similar to the rreg results. The benefits of rreg is that it deals not only with the serious problems (like dc being a very bad outlier) but also minor problems as well.
regress murder pctmetro poverty pcths single if state != "dc"
Source | SS df MS Number of obs = 50
-------------+------------------------------ F( 4, 45) = 39.88
Model | 606.611746 4 151.652936 Prob > F = 0.0000
Residual | 171.137027 45 3.80304505 R-squared = 0.7800
-------------+------------------------------ Adj R-squared = 0.7604
Total | 777.748773 49 15.8724239 Root MSE = 1.9501
------------------------------------------------------------------------------
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0534333 .013795 3.87 0.000 .0256488 .0812178
poverty | .2237151 .1185554 1.89 0.066 -.0150679 .462498
pcths | -.1938711 .0812756 -2.39 0.021 -.3575685 -.0301737
single | 1.388337 .2217525 6.26 0.000 .9417051 1.83497
_cons | -.0044014 7.478803 -0.00 1.000 -15.06748 15.05868
------------------------------------------------------------------------------
Let’s try running the results using qreg and compare them with rreg.
qreg murder pctmetro poverty pcths single
Iteration 1: WLS sum of weighted deviations = 187.90652
Iteration 1: sum of abs. weighted deviations = 177.16784
Iteration 2: sum of abs. weighted deviations = 167.01302
Iteration 3: sum of abs. weighted deviations = 128.40282
Iteration 4: sum of abs. weighted deviations = 125.28249
Iteration 5: sum of abs. weighted deviations = 124.226
Iteration 6: sum of abs. weighted deviations = 122.93248
Iteration 7: sum of abs. weighted deviations = 122.6427
Iteration 8: sum of abs. weighted deviations = 122.40488
Iteration 9: sum of abs. weighted deviations = 122.03476
Iteration 10: sum of abs. weighted deviations = 122.03096
Median regression Number of obs = 51
Raw sum of deviations 235.3 (about 6.8000002)
Min sum of deviations 122.031 Pseudo R2 = 0.4814
------------------------------------------------------------------------------
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0527879 .0226177 2.33 0.024 .0072608 .098315
poverty | .0908506 .1831176 0.50 0.622 -.2777461 .4594473
pcths | -.2686652 .1284197 -2.09 0.042 -.5271606 -.0101697
single | 1.796151 .2859057 6.28 0.000 1.220652 2.371649
_cons | 3.524669 11.34322 0.31 0.757 -19.30806 26.35739
------------------------------------------------------------------------------
rreg murder pctmetro poverty pcths single
Huber iteration 1: maximum difference in weights = .44857261
Huber iteration 2: maximum difference in weights = .0399983
Biweight iteration 3: maximum difference in weights = .15321379
Biweight iteration 4: maximum difference in weights = .00973214
Robust regression estimates Number of obs = 50
F( 4, 45) = 35.25
Prob > F = 0.0000
------------------------------------------------------------------------------
murder | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
pctmetro | .0535439 .0146555 3.65 0.001 .0240262 .0830615
poverty | .182561 .1259505 1.45 0.154 -.0711163 .4362383
pcths | -.2245853 .0863452 -2.60 0.013 -.3984936 -.0506771
single | 1.392942 .2355845 5.91 0.000 .9184503 1.867434
_cons | 2.888033 7.945302 0.36 0.718 -13.11463 18.89069
------------------------------------------------------------------------------
While the coefficients do not always match up, the variables that were significant in the qreg are also significant in the rreg and likewise for the non-significant variables. Even though these techniques use different strategies for resisting the influence of very deviant observations, they both arrive at the same conclusions regarding which variables are significantly related to murder, although they do not always agree in the strength of the relationship, i.e. the size of the coefficients.
2. Using the elemapi2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 ) pretend that 550 is the lowest score that a school could achieve on api00, i.e., create a new variable with the api00 score and recode it such that any score of 550 or below becomes 550. Use meals, ell and emer to predict api scores using 1) OLS to predict the original api score (before recoding) 2) OLS to predict the recoded score where 550 was the lowest value, and 3) using tobit to predict the recoded api score indicating the lowest value is 550. Compare the results of these analyses.
Answer 2.
First, we will use the elemapi2 data file and create the recoded version
of the api score where the lowest value is 550. We will call this value api00x.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 , clear gen api00x = api00 replace api00x = 550 if api00 <= 550 (122 real changes made)
Analysis 1. Now, we will run an OLS regression on the un-recoded version of api.
regress api00 meals ell emer
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 673.00
Model | 6749782.75 3 2249927.58 Prob > F = 0.0000
Residual | 1323889.25 396 3343.15467 R-squared = 0.8360
-------------+------------------------------ Adj R-squared = 0.8348
Total | 8073672.00 399 20234.7669 Root MSE = 57.82
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meals | -3.159189 .1497371 -21.10 0.000 -3.453568 -2.864809
ell | -.9098732 .1846442 -4.93 0.000 -1.272878 -.5468678
emer | -1.573496 .293112 -5.37 0.000 -2.149746 -.9972456
_cons | 886.7033 6.25976 141.65 0.000 874.3967 899.0098
------------------------------------------------------------------------------
Analysis 2. Now, we run an OLS regression on the recoded version of api.
regress api00x meals ell emerSource | SS df MS Number of obs = 400 -------------+------------------------------ F( 3, 396) = 682.88 Model | 4567355.46 3 1522451.82 Prob > F = 0.0000 Residual | 882862.941 396 2229.45187 R-squared = 0.8380 -------------+------------------------------ Adj R-squared = 0.8368 Total | 5450218.40 399 13659.6952 Root MSE = 47.217 ------------------------------------------------------------------------------ api00x | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- meals | -3.010788 .1222786 -24.62 0.000 -3.251184 -2.770392 ell | -.3034092 .1507844 -2.01 0.045 -.5998472 -.0069713 emer | -.7484733 .2393616 -3.13 0.002 -1.219052 -.277895 _cons | 869.31 5.111854 170.06 0.000 859.2602 879.3597 ------------------------------------------------------------------------------
Analysis 3. And we use tobit to perform the analysis indicating that the lowest value possible was 550.
tobit api00x meals ell emer , ll(550)
Tobit estimates Number of obs = 400
LR chi2(3) = 660.74
Prob > chi2 = 0.0000
Log likelihood = -1581.8117 Pseudo R2 = 0.1728
------------------------------------------------------------------------------
api00x | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meals | -3.145065 .1595799 -19.71 0.000 -3.458792 -2.831337
ell | -.8633529 .212474 -4.06 0.000 -1.281068 -.4456381
emer | -1.470878 .3361215 -4.38 0.000 -2.131678 -.8100772
_cons | 885.2395 6.372871 138.91 0.000 872.7107 897.7683
-------------+----------------------------------------------------------------
_se | 57.12718 2.473494 (Ancillary parameter)
------------------------------------------------------------------------------
Obs. summary: 122 left-censored observations at api00x <=550 278 uncensored observations
First, let’s compare analysis 1 and 2. When the range in api was restricted in analysis 2, the size of the coefficients dropped due to the restriction in range of the api scores. For example, the coefficient for ell dropped from -.9 to -.3 and its significance level changed to 0.045 (nearly not significant from being quite significant). Let’s see how well the tobit analysis compensated for the restriction in range by comparing analysis #1 and #3. The coefficients are quite similar in these two analyses. The standard errors are slightly larger in the tobit analysis leading the t values to be somewhat smaller. Nevertheless, the tobit estimates are much more on target than the second OLS analysis on the recoded data.
3. Using the elemapi2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 ) pretend that only schools with api scores of 550 or higher were included in the sample. Use meals ell and emer to predict api scores using 1) OLS to predict api from the full set of observations, 2) OLS to predict api using just the observations with api scores of 550 or higher, and 3) using truncreg to predict api using just the observations where api is 550 or higher. Compare the results of these analyses.
Answer 3.
First, we use the elemapi2 data file and run the analysis on the complete
data.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear
Analysis 1 using all of the data.
regress api00 meals ell emer
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 673.00
Model | 6749782.75 3 2249927.58 Prob > F = 0.0000
Residual | 1323889.25 396 3343.15467 R-squared = 0.8360
-------------+------------------------------ Adj R-squared = 0.8348
Total | 8073672.00 399 20234.7669 Root MSE = 57.82
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meals | -3.159189 .1497371 -21.10 0.000 -3.453568 -2.864809
ell | -.9098732 .1846442 -4.93 0.000 -1.272878 -.5468678
emer | -1.573496 .293112 -5.37 0.000 -2.149746 -.9972456
_cons | 886.7033 6.25976 141.65 0.000 874.3967 899.0098
------------------------------------------------------------------------------
Now let’s keep just the schools with api scores of 550 or higher for the next 2 analyses.
keep if api00 >= 550
(122 observations deleted)
Analysis 2 using OLS on just the schools with api scores of 550 or higher.
regress api00 meals ell emer
Source | SS df MS Number of obs = 278
-------------+------------------------------ F( 3, 274) = 292.55
Model | 2268727.43 3 756242.478 Prob > F = 0.0000
Residual | 708297.044 274 2585.02571 R-squared = 0.7621
-------------+------------------------------ Adj R-squared = 0.7595
Total | 2977024.48 277 10747.3808 Root MSE = 50.843
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meals | -2.798288 .1600331 -17.49 0.000 -3.113339 -2.483238
ell | -.3584496 .2315111 -1.55 0.123 -.8142161 .0973169
emer | -.9417814 .3547208 -2.65 0.008 -1.640106 -.2434569
_cons | 868.222 5.880858 147.64 0.000 856.6446 879.7994
------------------------------------------------------------------------------
Analysis 3 using truncreg on just the schools with api scores of 550 or higher.
truncreg api00 meals ell emer , ll(550)
(note: 0 obs. truncated)
Fitting full model:
Iteration 0: log likelihood = -1467.4296
Iteration 1: log likelihood = -1460.6163
Iteration 2: log likelihood = -1460.3638
Iteration 3: log likelihood = -1460.3636
Iteration 4: log likelihood = -1460.3636
Truncated regression
Limit: lower = 550 Number of obs = 278
upper = +inf Wald chi2(3) = 634.48
Log likelihood = -1460.3636 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
api00 | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
eq1 |
meals | -2.90758 .1872438 -15.53 0.000 -3.274571 -2.540589
ell | -.8212468 .2983573 -2.75 0.006 -1.406016 -.2364771
emer | -1.446235 .4549632 -3.18 0.001 -2.337946 -.5545233
_cons | 879.4212 6.595712 133.33 0.000 866.4939 892.3486
-------------+----------------------------------------------------------------
sigma |
_cons | 53.34897 2.545858 20.96 0.000 48.35918 58.33876
------------------------------------------------------------------------------
Let’s first compare the results of analysis 1 with analysis 2. When the schools with api scores of less than 550 are omitted, the coefficient for ell drops from -.9 to .35 and becomes no longer statistically significant. The coefficients for meals and emer remain significant although they both drop as well.
Now, let’s compare analysis 3 using truncreg with the original OLS analysis of the complete data. In both of these analyses, all of the variables are significant and the coefficients are quite similar, although the standard errors are larger in the truncreg. The truncreg did a pretty good job of showing us what the coefficients were in the complete sample based just on the restricted sample.
4. Using the hsb2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/hsb2 ) predict read from science, socst, math and write. Use the testparm and test commands to test the equality of the coefficients for science, socst and math. Use cnsreg to estimate a model where these three parameters are equal.
Answer 4.
We start by using the hsb2 data file.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/hsb2 , clear
(highschool and beyond (200 cases))
We first run an ordinary regression predicting read from science, socst, math and write.
regress read science socst math write
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 4, 195) = 69.74
Model | 12312.7853 4 3078.19634 Prob > F = 0.0000
Residual | 8606.63466 195 44.136588 R-squared = 0.5886
-------------+------------------------------ Adj R-squared = 0.5801
Total | 20919.42 199 105.122714 Root MSE = 6.6435
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
science | .2736751 .064369 4.25 0.000 .1467263 .4006238
socst | .273267 .0574246 4.76 0.000 .160014 .38652
math | .3028976 .072581 4.17 0.000 .1597532 .446042
write | .1104172 .0713398 1.55 0.123 -.0302795 .2511139
_cons | 1.946078 3.087346 0.63 0.529 -4.142797 8.034954
------------------------------------------------------------------------------
We use the testparm command to test that the coefficients for science, socst and math are equal.
testparm science socst math, equal
( 1) - science + socst = 0.0
( 2) - science + math = 0.0
F( 2, 195) = 0.05
Prob > F = 0.9554
We can also use the test command to test that the coefficients for science, socst and math are equal.
test science=socst
( 1) science - socst = 0.0
F( 1, 195) = 0.00
Prob > F = 0.9964
test socst=math, accum
( 1) science - socst = 0.0
( 2) socst - math = 0.0
F( 2, 195) = 0.05
Prob > F = 0.9554
We now constrain these three coefficients to be equal.
constraint define 1 science = socst constraint define 2 socst = math
And we use cnsreg to estimate the model with these constraints in place.
cnsreg read science socst math write, c(1 2)
Constrained linear regression Number of obs = 200
F( 2, 197) = 140.80
Prob > F = 0.0000
Root MSE = 6.6113
( 1) science - socst = 0.0
( 2) socst - math = 0.0
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
science | .2828596 .0268291 10.54 0.000 .2299505 .3357687
socst | .2828596 .0268291 10.54 0.000 .2299505 .3357687
math | .2828596 .0268291 10.54 0.000 .2299505 .3357687
write | .1106022 .0708452 1.56 0.120 -.02911 .2503145
_cons | 2.012299 3.061703 0.66 0.512 -4.025622 8.05022
------------------------------------------------------------------------------
5. Using the elemapi2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 ) consider the following 2 regression equations.
api00 = meals ell emer api99 = meals ell emer
Estimate the coefficients for these predictors in predicting api00 and api99 taking into account the non-independence of the schools. Test the overall contribution of each of the predictors in jointly predicting api scores in these two years. Test whether the contribution of emer is the same for api00 and api99.
Answer 5.
First, let’s use the elemapi2 data file.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear
Next, let’s analysze these equations separately.
regress api00 meals ell emer
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 673.00
Model | 6749782.75 3 2249927.58 Prob > F = 0.0000
Residual | 1323889.25 396 3343.15467 R-squared = 0.8360
-------------+------------------------------ Adj R-squared = 0.8348
Total | 8073672.00 399 20234.7669 Root MSE = 57.82
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meals | -3.159189 .1497371 -21.10 0.000 -3.453568 -2.864809
ell | -.9098732 .1846442 -4.93 0.000 -1.272878 -.5468678
emer | -1.573496 .293112 -5.37 0.000 -2.149746 -.9972456
_cons | 886.7033 6.25976 141.65 0.000 874.3967 899.0098
------------------------------------------------------------------------------
regress api99 meals ell emer
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 716.31
Model | 7293890.24 3 2431296.75 Prob > F = 0.0000
Residual | 1344092.70 396 3394.17349 R-squared = 0.8444
-------------+------------------------------ Adj R-squared = 0.8432
Total | 8637982.94 399 21649.08 Root MSE = 58.26
------------------------------------------------------------------------------
api99 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meals | -3.412388 .1508754 -22.62 0.000 -3.709004 -3.115771
ell | -.793822 .1860477 -4.27 0.000 -1.159587 -.4280573
emer | -1.516305 .2953401 -5.13 0.000 -2.096936 -.9356748
_cons | 860.191 6.307343 136.38 0.000 847.7909 872.591
------------------------------------------------------------------------------
Now, let’s analyze them using sureg that takes into account the non-independence of these equations.
sureg (api00 api99 = meals ell emer)
Seemingly unrelated regression
----------------------------------------------------------------------
Equation Obs Parms RMSE "R-sq" chi2 P
----------------------------------------------------------------------
api00 400 3 57.53019 0.8360 2039.38 0.0000
api99 400 3 57.96751 0.8444 2170.651 0.0000
----------------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
api00 |
meals | -3.159189 .1489866 -21.20 0.000 -3.451197 -2.86718
ell | -.9098732 .1837186 -4.95 0.000 -1.269955 -.5497913
emer | -1.573496 .2916428 -5.40 0.000 -2.145105 -1.001886
_cons | 886.7033 6.228382 142.36 0.000 874.4959 898.9107
-------------+----------------------------------------------------------------
api99 |
meals | -3.412388 .1501191 -22.73 0.000 -3.706616 -3.11816
ell | -.793822 .1851151 -4.29 0.000 -1.156641 -.431003
emer | -1.516305 .2938597 -5.16 0.000 -2.09226 -.9403509
_cons | 860.191 6.275727 137.07 0.000 847.8908 872.4912
------------------------------------------------------------------------------
We can test the contribution of meals ell and emer as shown below.
test meals
( 1) [api00]meals = 0.0
( 2) [api99]meals = 0.0
chi2( 2) = 518.30
Prob > chi2 = 0.0000
test ell
( 1) [api00]ell = 0.0
( 2) [api99]ell = 0.0
chi2( 2) = 24.80
Prob > chi2 = 0.0000
test emer
( 1) [api00]emer = 0.0
( 2) [api99]emer = 0.0
chi2( 2) = 29.48
Prob > chi2 = 0.0000
We can test whether the coefficients for emer were the same in predicting api00 and api99 as shown below.
test [api00]emer = [api99]emer
( 1) [api00]emer - [api99]emer = 0.0
chi2( 1) = 0.21
Prob > chi2 = 0.6456
We can also test the contribution of meals ell and emer using more traditional multivariate tests using the mvreg and mvtest commands as shown below.
mvreg api00 api99 = meals ell emer
Equation Obs Parms RMSE "R-sq" F P
----------------------------------------------------------------------
api00 400 4 57.82002 0.8360 672.9954 0.0000
api99 400 4 58.25954 0.8444 716.3148 0.0000
------------------------------------------------------------------------------
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
api00 |
meals | -3.159189 .1497371 -21.10 0.000 -3.453568 -2.864809
ell | -.9098732 .1846442 -4.93 0.000 -1.272878 -.5468678
emer | -1.573496 .293112 -5.37 0.000 -2.149746 -.9972456
_cons | 886.7033 6.25976 141.65 0.000 874.3967 899.0098
-------------+----------------------------------------------------------------
api99 |
meals | -3.412388 .1508754 -22.62 0.000 -3.709004 -3.115771
ell | -.793822 .1860477 -4.27 0.000 -1.159587 -.4280573
emer | -1.516305 .2953401 -5.13 0.000 -2.096936 -.9356748
_cons | 860.191 6.307343 136.38 0.000 847.7909 872.591
------------------------------------------------------------------------------
Below we show the multivariate tests for meals ell and for emer.
mvtest meals
MULTIVARIATE TESTS OF SIGNIFICANCE
Multivariate Test Criteria and Exact F Statistics for
the Hypothesis of no Overall "meals" Effect(s)
S=1 M=0 N=196.5
Test Value F Num DF Den DF Pr > F
Wilks' Lambda 0.43558762 255.9105 2 395.0000 0.0000
Pillai's Trace 0.56441238 255.9105 2 395.0000 0.0000
Hotelling-Lawley Trace 1.29574936 255.9105 2 395.0000 0.0000
mvtest ell
MULTIVARIATE TESTS OF SIGNIFICANCE
Multivariate Test Criteria and Exact F Statistics for
the Hypothesis of no Overall "ell" Effect(s)
S=1 M=0 N=196.5
Test Value F Num DF Den DF Pr > F
Wilks' Lambda 0.94161436 12.2462 2 395.0000 0.0000
Pillai's Trace 0.05838564 12.2462 2 395.0000 0.0000
Hotelling-Lawley Trace 0.06200590 12.2462 2 395.0000 0.0000
mvtest emer
MULTIVARIATE TESTS OF SIGNIFICANCE
Multivariate Test Criteria and Exact F Statistics for
the Hypothesis of no Overall "emer" Effect(s)
S=1 M=0 N=196.5
Test Value F Num DF Den DF Pr > F
Wilks' Lambda 0.93136794 14.5537 2 395.0000 0.0000
Pillai's Trace 0.06863206 14.5537 2 395.0000 0.0000
Hotelling-Lawley Trace 0.07368952 14.5537 2 395.0000 0.0000