- Introduction
- Binary Logistic Regression
- Exact Logistic Regression
- Generalized Logits Model – Multinomial Logistic Regression
- Proportional Odds Model – Ordinal Logistic Regression
Introduction
Logistic regression describes the relationship between a categorical response variable and a set of predictor variables. A categorical response variable can be a binary variable, an ordinal variable or a nominal variable. Each type of categorical variables requires different techniques to model its relationship with the predictor variables. In this seminar, we illustrate how to perform different types of analyses using SAS proc logistic. For a binary response variable, such as a response to a yes-no question, a commonly used model is the logistic regression model. We also touch the surface of exact logistic regression, which is very useful when the sample size is too small or the events are too sparse. For a nominal response variable, such as Democrats, Republicans and Independents, we can fit a generalized logits model. For an ordinal response variable, such as low, medium and high, we can fit it to a proportional odds model.
Logistic Regression Models
In this section, we will use the High School and Beyond data set, hsb2 to describe what a logistic model is, how to perform a logistic regression model analysis and how to interpret the model. Our dependent variable is created as a dichotomous variable indicating if a student’s writing score is higher than or equal to 52. We call it hiwrite. The predictor variables will include prog, female and other test scores. Our data set has 200 observations.
data hsb2; set hsb2; hiwrite = write >=52; run;
proc means data = hsb2 mean std; run;
Variable Mean Std Dev ---------------------------------------- ID 100.5000000 57.8791845 FEMALE 0.5450000 0.4992205 RACE 3.4300000 1.0394722 SES 2.0550000 0.7242914 SCHTYP 1.1600000 0.3675260 PROG 2.0250000 0.6904772 READ 52.2300000 10.2529368 WRITE 52.7750000 9.4785860 MATH 52.6450000 9.3684478 SCIENCE 51.8500000 9.9008908 SOCST 52.4050000 10.7357935 hiwrite 0.6300000 0.4840159 ----------------------------------------
Let π be the probability of scoring higher than 51 in writing test. The odds is π/(1-π). For example, the overall probability of scoring higher than 51 is .63. The odds will be .63/(1-.63) = 1.703. A logistic regression model describes a linear relationship between the logit, which is the log of odds, and a set of predictors.
logit(π) = log(π/(1-π)) = α + β1*x1 + + … + βk*xk = α + x β
We can either interpret the model using the logit scale, or we can convert the log of odds back to the probability such that
β)).
The advantage of using the logit scale for interpretation is that the relationship between the logit and the predictors is a linear relationship. But sometimes it is easier to interpret the model in terms of probabilities. Then we have to keep in mind that the relationship between the probabilities and the predictors is not a linear relationship. For more details on odds ratio, please see our FAQ page on how to interpret odds ratios in logistic regression.
A Simple Model
Let’s consider the model where female is the only predictor. We will use this example to understand the concepts of odds and odds ratios and to understand how they are related to the parameter estimates.
proc logistic data = hsb2 ; model hiwrite (event='1') = female ; ods output ParameterEstimates = model_female; run;
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.0220 0.2097 0.0110 0.9165 FEMALE 1 0.9928 0.3016 10.8369 0.0010
Notice that we can specify which event to model using the event = option in the model statement. This is new in SAS 8.2. The other way of specifying that we want to model 1 as event instead of 0 is to use the descending option in the proc logistic statement. One thing that is worth noticing is the use of quotes in the option event = ‘1’. Even though, the variable hiwrite is a numeric variable, it is still necessary to surround 1 with a pair of quotes. It comes handy when the outcome variable is coded as a character variable. Using the ODS output statement, we created a data set called model_female containing the parameter estimates shown above. We can then use the data set to create the odds and odds ratio.
data model_fem; set model_female; o = exp(estimate); run; proc print data = model_fem; var variable estimate o; run;
Obs Variable Estimate o
1 Intercept 0.0220 1.02222 2 FEMALE 0.9928 2.69865
The intercept has a parameter estimate of .022. This is the estimated logit when female = 0, that is when the student is a male student. Therefore, the odds = exp(logit) = exp(.0220) = 1.02222 is the estimated odds for a male student to score 52 or higher in writing test. The coefficient for variable female is .9928. That means that for a one unit increase in female (that is changing from male to female) the expected change in log of odds is .9928. We can also interpret it in the scale of odds ratio. The odds for a male student is exp() = exp(.022) and the odds for a female student is exp(.022 + .9928*1). Therefore, taking the ratio of these two odds, we get the odds ratio for female versus male is exp(.9928) = 2.699.
In terms of probabilities, the probability for females to score 52 or higher on the writing test is exp(.022 + .9928) / (1 + exp(.022 + .9928)) = .734. The probability for males is exp(.022 )/(1 + exp(.022)) = .505.
With this simple example, we can actually compute the odds ratio from the 2×2 table of hiwrite*female.
proc freq data = hsb2; tables hiwrite*female /nocum nopercent; run;
hiwrite FEMALE
Frequency|
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
0 | 45 | 29 | 74
| 60.81 | 39.19 |
| 49.45 | 26.61 |
---------+--------+--------+
1 | 46 | 80 | 126
| 36.51 | 63.49 |
| 50.55 | 73.39 |
---------+--------+--------+
Total 91 109 200
For example, for males, the odds is 46/45 = 1.022, which is the exponentiated value of the intercept from the model. The odds ratio for females versus males is (80/29)/(46/45) = 2.699. It is usually written as a cross-product (45*80)/(29*46) = 2.699. This is the exponentiated value of the parameter estimate for variable female.
A Model with a Continuous Predictor and a Categorical Predictor
Let’s now take a look at a model with both a continuous variable math and a categorical variable female as predictors. We will focus on how to interpret the parameter estimate for the continuous variable.
proc logistic data = hsb2; model hiwrite (event='1') = female math; output out = m2 p = prob xbeta = logit; run;
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -10.3651 1.5535 44.5153 <.0001 FEMALE 1 1.6304 0.4052 16.1922 <.0001 MATH 1 0.1979 0.0293 45.5559 <.0001
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits
FEMALE 5.106 2.308 11.298 MATH 1.219 1.151 1.291
The interpretation for the parameter estimate of math is very similar to that for the categorical variable female. In terms of logit scale, we can say that for every unit increase in the math score, the logit will increase by .198, holding everything else constant. We can also say that for a one unit increase in math score, the odds of scoring 51 or higher in writing test increases by (1.219-1)*100% = 22%.
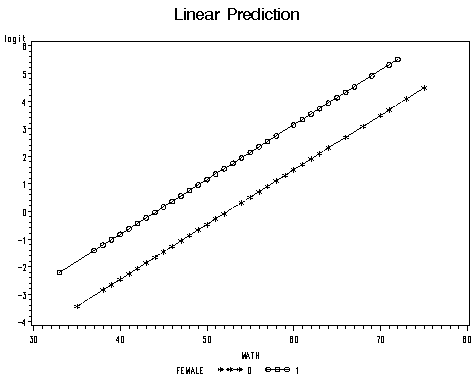
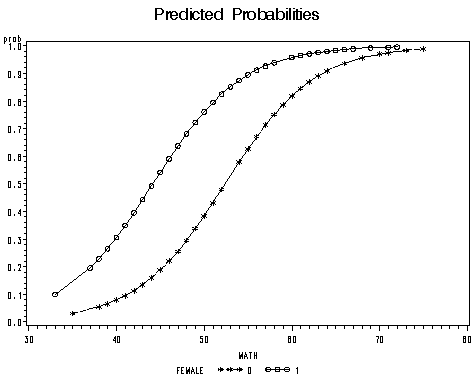
We used an output statement to create a data set containing the predicted probabilities based on the model. We can compare the linear predictions and the probabilities in terms of the math scores for the males and females.
proc sort data = m2; by math; run;
symbol1 i = join v=star l=32 c = black; symbol2 i = join v=circle l = 1 c=black; proc gplot data = m2; plot logit*math = female; plot prob*math = female; run; quit;
Sometimes, a one unit change may not be a desirable scale to use. We can ask SAS to give us odds ratio for different units of change. For example, it may make more sense to talk about change of every 5 units in math score. This can be done using units statement. We also include the option clodds = wald to the model statement so that the confidence interval will also be calculated for the odds ratio calculated in the unit statement. Of course, you can always manually compute the odds ratio for every 5 units change in math score as 1.219^5 = 2.69.
proc logistic data = hsb2 ;
model hiwrite (event='1') = female math /clodds=wald;
units math = 5;
run;
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits FEMALE 5.106 2.308 11.298 MATH 1.219 1.151 1.291
Wald Confidence Interval for Adjusted Odds Ratios
Effect Unit Estimate 95% Confidence Limits MATH 5.0000 2.689 2.018 3.584
Other Features of Proc Logistic
We will illustrate other features of proc logistic by using a model with more predictors. We will include categorical variables prog and female, continuous variables math and read. This model is merely for the purpose of demonstrating proc logistic, not really a model developed based on any theory.
proc logistic data = hsb2 ;
class prog (ref='1') /param = ref;
model hiwrite (event='1') = female read math prog ;
run;
Response Profile
Ordered Total Value hiwrite Frequency
1 0 74
2 1 126
Probability modeled is hiwrite=1.
Class Level Information
Design Class Value Variables
PROG 1 0 0
2 1 0
3 0 1
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -12.3140 2.0374 36.5311 <.0001 FEMALE 1 1.9576 0.4533 18.6541 <.0001 READ 1 0.1037 0.0298 12.1453 0.0005 MATH 1 0.1310 0.0329 15.8738 <.0001 PROG 2 1 0.2721 0.4889 0.3098 0.5778 PROG 3 1 -0.5776 0.5478 1.1116 0.2917
CLASS statement Notice that we have used the class statement for variable prog. SAS will create dummy variables for a categorical variable on-the-fly. There are various coding schemes from which to choose. The default coding for all the categorical variables in proc logistic is the effect coding. Here we changed it to dummy coding by using the param = ref option. We can specify the comparison group by using ref = option after the variable name. There are other coding schemes available, such as orthogonal polynomial coding scheme and reference cell coding. We can double check what coding scheme is used and which group is the reference group by looking at the Class Level Information part of the output.
CONTRAST statement
In the parameter estimates, we only see the comparison of level 2 vs. 1 and level 3 vs. 1 for variable prog. If we want to compare level 2 vs. level 3, we can use the contrast statement. Usually, contrast is done using less than full rank, reference cell coding as used in proc glm. We chose this type of coding by using param = glm option in the class statement. We also used estimate option at the end of contrast statement to get the estimate of the difference between group 1 and group 2. It is always a good idea to check the Class Level Information to see how the variable is coded so we know that the contrast statement gives us the expected contrast among groups.
proc logistic data = hsb2 ; class prog /param = glm ; model hiwrite (event='1') = female read math prog; contrast '1 vs 2 of prog' prog 1 -1 0 / estimate; run;
Class Level Information
Class Value Design Variables
PROG 1 1 0 0
2 0 1 0
3 0 0 1
Contrast Test Results
Wald Contrast DF Chi-Square Pr > ChiSq
1 vs 2 of prog 1 0.3098 0.5778
Contrast Rows Estimation and Testing Results
Standard Contrast Type Row Estimate Error Alpha Confidence Limits
1 vs 2 of prog PARM 1 -0.2721 0.4889 0.05 -1.2303 0.6861
Contrast Rows Estimation and Testing Results
Wald Contrast Type Row Chi-Square Pr > ChiSq
1 vs 2 of prog PARM 1 0.3098 0.5778
TEST Statement
The parameter estimates offers all the one degree of freedom test on each of the parameters. We can also test the combined effect of multiple parameters using the test statement. In the example below, we first tested on the joint effect of read and math. Next we tested on the hypothesis that the effect of read and math are the same.
proc logistic data = hsb2 ; class prog(ref='1') /param = ref; model hiwrite (event='1') = prog female read math; test_read_math: test read, math; test_equal: test read = math; run; Linear Hypotheses Testing Results
Wald Label Chi-Square DF Pr > ChiSq
test_read_math 37.2236 2 <.0001 test_equal 0.3041 1 0.5813
LACKFIT and RSQUARE Option
The Hosmer-Lemeshow test of goodness-of-fit can be performed by using the lackfit option after the model statement. This test divides subjects into deciles based on predicted probabilities, then computes a chi-square from observed and expected frequencies. It tests the null hypothesis that there is no difference between the observed and predicted values of the response variable. Therefore, when the test is not significant, as in this example, we can not reject the null hypothesis and say that the model fits the data well. We can also request the generalized R-square measure for the model by using rsquare option after the model statement. SAS gives the likelihood-based pseudo R-square measure and its rescaled measure. Categorical Data Analysis Using The SAS System, by M. Stokes, C. Davis and G. Koch offers more details on how the generalized R-square measures that you can request are constructed and how to interpret them.
proc logistic data = hsb2;
class prog(ref='1') /param = ref;
model hiwrite(event='1') = female prog read math / rsq lackfit;
run;
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 265.582 167.035
SC 268.881 186.825
-2 Log L 263.582 155.035
R-Square 0.4188 Max-rescaled R-Square 0.5720
Partition for the Hosmer and Lemeshow Test
hiwrite = 1 hiwrite = 0
Group Total Observed Expected Observed Expected
1 20 0 1.08 20 18.92
2 20 4 3.45 16 16.55
3 20 9 6.54 11 13.46
4 21 10 10.86 11 10.14
5 20 13 13.64 7 6.36
6 20 17 15.70 3 4.30
7 20 16 17.44 4 2.56
8 20 18 18.76 2 1.24
9 20 20 19.61 0 0.39
10 19 19 18.90 0 0.10
Hosmer and Lemeshow Goodness-of-Fit Test
Chi-Square DF Pr > ChiSq
5.2766 8 0.7276
Influence Statistics
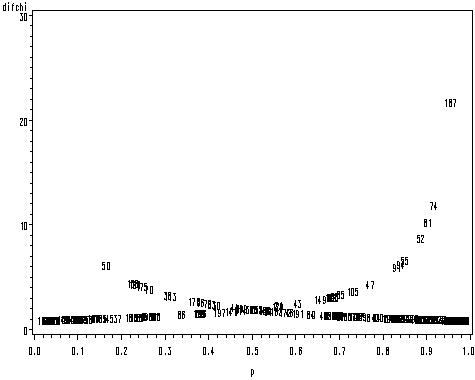
One important topic in logistic regression is regression diagnostics. Proc logistic can generate a lot of diagnostic measures for detecting outliers and influential data points for a binary outcome variable. These diagnostic measures can be requested by using the output statement. For example, we can request for residual deviance, the hat matrix diagonal and residual chi-squared deviance and the difference between chi-square goodness-of-fit when an observation is deleted. We can then plot these variables against the predicted values to investigate the influence of each point on the model. By using the pointlabel option in the symbol statement, we can see that the observation with id = 187 has the highest influence on the chi-square goodness-of-fit.
proc logistic data = hsb2 ;
class prog(ref='1') /param = ref;
model hiwrite(event='1') = female prog read math ;
output out=dinf prob=p resdev=dr h=pii reschi=pr difchisq=difchi;
run;
goptions reset = all;
symbol1 pointlabel = ("#id" h=1 ) value=none;
proc gplot data = dinf;
plot difchi*p;
run;
quit;
Scoring a New Data Set
There are situations where we want to produce predicted probabilities for a specific combination of the values of the predictors. For example, we may want to know the predicted probabilities for groups defined by female and prog when math and read are held at their grand means. Let’s first create a data set with the groups and grand means for math and read.
proc sql;
create table gdata as
select distinct female, (prog=2) as prog2,(prog=3) as prog3,
mean(read) as read, mean(math) as math
from hsb2;
quit;
proc print data = gdata;
run;
Obs FEMALE prog2 prog3 read math
1 0 0 0 52.23 52.645 2 0 0 1 52.23 52.645 3 0 1 0 52.23 52.645 4 1 0 0 52.23 52.645 5 1 0 1 52.23 52.645 6 1 1 0 52.23 52.645
We can use SAS proc score to generate the linear predicted values and then compute the odds or probabilities afterwards. Notice that the score procedure does not care what model we have run. It uses the estimated parameters to generate linear predictions. In our logistic regression case, the predicted values are therefore in the logit scale. In the output data set created by proc score, we have a variable called hiwrite. This is the new variable that proc score created for predicted values.
proc logistic data = hsb2 outest=mg; class prog(ref='1') /param = ref; model hiwrite(event='1') = female prog read math ; run; *Scoring the data set to get the linear predictions; proc score data=gdata score=mg out=gpred type=parms; var female prog2 prog3 read math; run; data gpred; set gpred; odds = exp(hiwrite); p_1 = odds /(1+odds); p_0 = 1 - p_1; run; proc print data = gpred; run;
Obs FEMALE prog2 prog3 read math hiwrite odds p_1 p_0
1 0 0 0 52.23 52.645 0.00012 1.00012 0.50003 0.49997 2 0 0 1 52.23 52.645 -0.57747 0.56132 0.35952 0.64048 3 0 1 0 52.23 52.645 0.27223 1.31289 0.56764 0.43236 4 1 0 0 52.23 52.645 1.95774 7.08332 0.87629 0.12371 5 1 0 1 52.23 52.645 1.38016 3.97552 0.79902 0.20098 6 1 1 0 52.23 52.645 2.22986 9.29856 0.90290 0.09710
Remarks: This process will be simplified with SAS 9.0 and above with the new statement score in proc logistic. The syntax one will use looks like the following:
proc sql; create table gdata1 as select distinct female, ses, mean(read) as read, mean(math) as math from hsb2; quit; proc logistic data = hsb2 outmodel=mg1; class prog(ref='1') /param = ref; model hiwrite(event='1') = female prog read math ; run; proc logistic inmodel=mg1; score data = gdata1 out=gpred1; run; proc print data = gpred1; run;
Exact Logistic Regression
All of the models we have inspected so far require large sample sizes. When the data sets are too small or when the event occurs very infrequently, the maximum likelihood method may not work or may not provide reliable estimates. Exact logistic regression provides a way to get around these difficulties. What it does is to enumerate the exact distributions of the parameters of interest, conditional on the remaining parameters. Here is a simple example from Performing Exact Logistic Regression with the SAS System. The data set has very small cells, with each cell having only 3 observations. Let’s run the exact logistic regression on this data set.
data dose; input dose deaths total; datalines; 0 0 3 1 0 3 2 0 3 3 0 3 4 1 3 5 2 3 ; run;
proc logistic data = dose desc;
model deaths/total = dose;
exact dose /estimate = both;
run;
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 18.220 12.072
SC 19.111 13.853
-2 Log L 16.220 8.072
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 8.1478 1 0.0043 Score 5.7943 1 0.0161 Wald 2.7249 1 0.0988
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -9.4745 5.5677 2.8958 0.0888 dose 1 2.0804 1.2603 2.7249 0.0988
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits dose 8.007 0.677 94.679
Exact Conditional Analysis
Conditional Exact Tests
--- p-Value ---
Effect Test Statistic Exact Mid
dose Score 5.4724 0.0245 0.0190
Probability 0.0110 0.0245 0.0190
Exact Parameter Estimates
95% Confidence Parameter Estimate Limits p-Value dose 1.8000 0.1157 5.8665 0.0245
Exact Odds Ratios
95% Confidence Parameter Estimate Limits p-Value dose 6.049 1.123 353.000 0.0245
Notice first of all that the syntax for model statement is slight different than we have seen so far. This is the syntax used for grouped data. That is we have frequencies of the events for each of the cells. This type of syntax works for both the maximum likelihood logistic regression and exact logistic regression. With estimate = both, we request that both the parameters and the odds ratios are being estimated.
Generalized Logits Model for Multinomial Logistic Models
Proc logistic also perform analysis on nominal response variables. Since the response variable no longer has the ordering, we can no longer fit a proportional odds model to our data. But we can fit a generalized logits model. This analysis can be done using proc catmod and that is how it is used to be done. SAS 8.2 added some new features to its proc logistic and now proc logistic does analysis on nominal responses with ease. In this section, we are going to use a data file called school used in Categorical Data Analysis Using The SAS System, by M. Stokes, C. Davis and G. Koch. We will illustrate what a generalized logits model is and how to perform an analysis using proc logistic.
data school; input school program style $ count; cards; 1 1 self 10 1 1 team 17 1 1 class 26 1 2 self 5 1 2 team 12 1 2 class 50 2 1 self 21 2 1 team 17 2 1 class 26 2 2 self 16 2 2 team 12 2 2 class 36 3 1 self 15 3 1 team 15 3 1 class 16 3 2 self 12 3 2 team 12 3 2 class 20 ; run;
In this data set, three different teaching styles have been implemented in teaching third grade math. School children in experimental learning settings were surveyed to determine which teaching styles they preferred. The response variable style takes three values: class, self and team. We want to determine the preference of students by their schools and programs. The programs are regular and after-school programs with 1 being regular and 2 being after-school.
In a generalized logit model, we will pick a particular category of responses as the baseline reference and compare every other category with the baseline response. In our example, we will choose team as the baseline category. Consider the probabilities:
class’, π2 = probability of ‘Preferring self‘, π3 = probability of ‘Preferring team‘.
The generalized logits are defined as
logit(θ2) = log(π2/π3).
The generalized logits model for our example is then defined as
βi,
where i = 1 and 2 indicating the two logits. This means that we allow two different sets of regression parameters, one for each logit.
We can calculate the generalized odds from the frequency table, similar to what we have done in the case of proportional odds model.
proc freq data = school; weight count; tables style /list chisq relrisk; ods output OneWayFreqs = test; run; data test1; set test; godds = frequency/85; run; proc print data = test1; var style frequency godds; run;
Obs style Frequency godds
1 class 174 2.04706 2 self 79 0.92941 3 team 85 1.00000
The other way of getting the same results is to run the generalized logits model. In SAS, we can simply use proc logistic with the link = glogit option.
proc logistic data = school order = internal; freq count; model style = /link = glogit ; ods output parameterestimates= odds; run; data odds1; set odds; odds = exp(estimate); run; proc print data = odds1; var response estimate odds; run;
Obs Response Estimate odds
1 class 0.7164 2.04706 2 self -0.0732 0.92941
Saturated Model Example
In this data set, there are three schools and two types of programs. That is, for each of the preference choices there are possible six cell counts. If we use both school and program and also include their interaction, we will use up all the degrees of freedom. That is we have a saturated model. This is the best model we can get, fitting each cell with its own parameter.
proc logistic data=school order = internal; freq count; class school program / order = data; model style = school program school*program /link = glogit scale = none aggregate; run;
The LOGISTIC Procedure
Model Information
Data Set WORK.SCHOOL Response Variable style Number of Response Levels 3 Number of Observations 18 Frequency Variable count Sum of Frequencies 338 Model generalized logit Optimization Technique Fisher's scoring
Response Profile
Ordered Total Value style Frequency
1 class 174
2 self 79
3 team 85
Logits modeled use style='team' as the reference category.
Class Level Information
Design Class Value Variables
school 1 1 0
2 0 1
3 -1 -1
program 1 1
2 -1
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Deviance and Pearson Goodness-of-Fit Statistics
Criterion Value DF Value/DF Pr > ChiSq
Deviance 0.0000 0 . . Pearson 0.0000 0 . .
Number of unique profiles: 6
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 699.404 689.156 SC 707.050 735.033 -2 Log L 695.404 665.156
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 30.2480 10 0.0008 Score 28.3738 10 0.0016 Wald 25.6828 10 0.0042
Type 3 Analysis of Effects
Wald Effect DF Chi-Square Pr > ChiSq
school 4 14.5522 0.0057 program 2 10.4815 0.0053 school*program 4 1.7439 0.7827
We have included most parts of the output from SAS, excluding the parameter estimates. The Deviance and Pearson Goodness-of-Fit Statistics output is new here. They were requested by using option scale = none aggregate. Because our model is saturated, the goodness-of-fit statistics are zero with zero degree of freedom. We also see that the default type of coding scheme, e.g. effect coding, that proc logistic has for categorical variables. We also see that the overall effect of the interaction of school and program is not significant. This leads us to a simpler model with only the main effect.
Model With Only Main Effect
proc logistic data=school order = internal; freq count; class school program /order = data; model style = school program /link = glogit scale = none aggregate; run;
Odds Ratio Estimates
Point 95% Wald Effect style Estimate Confidence Limits
school 1 vs 3 class 1.926 0.990 3.747 school 1 vs 3 self 0.517 0.228 1.175 school 2 vs 3 class 1.609 0.820 3.155 school 2 vs 3 self 1.276 0.620 2.626 program 1 vs 2 class 0.476 0.280 0.809 program 1 vs 2 self 1.005 0.538 1.877
We will focus on the interpretation of parameters. For example the odds ratio of class to team for program1 versus program 2 is .476. We can say that the odds for students in program 1 to choose class over team is .476 times the odds for students in program 2. Or we can say that the odds for students in program 1 to choose class over team is .524 times less than the odds for students in program 2. Similarly, we can say that the odds for students in school 1 to choose class over team is 1.926 times the odds for students in school 3. Or we can say that the odds for
students in school 1 to choose class over team is .926 times more than the odds for students in school 3. It is oftentimes easier to describe in terms of probabilities. We can use the output statement to generate these probabilities as shown below.
proc logistic data=school order = internal; freq count; class school program ; model style = school program / link = glogit; output out = smodel p=prob; run; proc freq data = smodel; where school = 1 or school = 2; format prob 5.4; tables school*program*_level_*prob /list nopercent nocum; run;
school program _LEVEL_ prob Frequency
--------------------------------------------------
1 1 class .5371 3
1 1 self .1580 3
1 1 team .3049 3
1 2 class .7095 3
1 2 self .0989 3
1 2 team .1917 3
2 1 class .3924 3
2 1 self .3409 3
2 1 team .2667 3
2 2 class .5764 3
2 2 self .2372 3
2 2 team .1864 3
Proportional Odds Model for Ordinal Logistic Models
The proportional odds model is also referred as the logit version of an ordinal regression model. It extends logistic regression to handle ordinal response variables. In this section, we are going to use SAS data set https://stats.idre.ucla.edu/wp-content/uploads/2016/02/ordwarm2.sas7bdat to illustrate what a proportional odds model is and how to perform a proportional odds model analysis.
Let’s first take a look at the data set. This data set is taken from Regression Models For Categorical Dependent Variables Using Stata by Long and Freese. Each subject in the data set was asked to evaluate the following statement: “A working mother can establish just as warm and secure of a relationship with her child as a mother who does not work”. The response is recoded in a variable called warm. It has four levels: 1 = Strongly Disagree (SD), 2 = Disagree (D), 3 = Agree (A) and 4 = Strongly Agree (SA). This will be the response variable in our analysis. Other variables in the data set include age, education level, gender of the subject, and other subject related variables.
options nocenter nodate label; proc contents data = ordwarm2; run;
The CONTENTS Procedure
Data Set Name: WORK.ORDWARM2 Observations: 2293
Member Type: DATA Variables: 10
-----Alphabetic List of Variables and Attributes-----
# Variable Type Len Pos Label ------------------------------------------------------------------------------ 2 age Num 3 8 Age in years 3 ed Num 3 11 Years of education 5 male Num 3 17 Gender: 1=male 0=female 4 prst Num 3 14 Occupational prestige 1 warm Num 8 0 Mom can have warm relations with child 8 warmlt2 Num 3 26 1=SD; 0=D,A,SA 9 warmlt3 Num 3 29 1=SD,D; 0=A,SA 10 warmlt4 Num 3 32 1=SD,D,A; 0=SA 7 white Num 3 23 Race: 1=white 0=not white 6 yr89 Num 3 20 Survey year: 1=1989 0=1977
We are interested in building up a model to describe the relationship between the response variable warm and some of the explanatory variables, such as the age, level of education and race. Let’s consider the probabilities
θ1 = π1, probability of ‘Strongly Disagree’, θ2 = π1 + π2, probability of ‘Strongly Disagree’ or ‘Disagree’, θ3 = π1 + π2 + π3, probability of ‘Not Strongly Agree’,
where π1 = probability of ‘Strongly Disagree’, π2 = probability of ‘Disagree’, π3 = probability of ‘Agree’, π4 = probability of ‘Strongly Agree’.
logit(θ1) = log( θ1/(1 – θ1)) = log(π1/(π2 + π3 + π4)), logit(θ2) = log( θ2/(1 – θ2)) = log((π1 + π2)/(π3 + π4)), logit(θ3) = log( θ3/(1 – θ3)) = log((π1 + π2 + π3))/π4).
Thus we allow the intercept to be different for different cumulative logit functions, but the effect of the explanatory variables will be the same across different logit functions. That is, we allow different αs for each of the cumulative odds, but only one set of βs for all the cumulative odds. This is the proportionality assumption and this is why this type model is called proportional odds model. Also notice that although this is a model in terms of cumulative odds, we can always recover the probabilities of each response category
as follows.
π2 = θ2 – θ1 π3 = θ3 – θ2 π4 = 1 – θ3
We can calculate the cumulative odds from the frequency table.
proc freq data = ordwarm2; table warm ; ods output onewayfreqs = test (keep = warm frequency cumfrequency); run; data test1; set test; if _n_ <=3 then odds = cumfrequency /(2293-cumfrequency); run; proc print data= test1; run;
Cum Obs warm Frequency Frequency odds
1 1 297 297 0.14880 2 2 723 1020 0.80126 3 3 856 1876 4.49880 4 4 417 2293 .
The other way of getting the same result is to run a proportional odds model with only the intercept as a predictor.
proc logistic data = ordwarm2 ; model warm = /link = clogit; ods output ParameterEstimates = model_based; run; data test2; set model_based; odds = exp(estimate); run; proc print data = test2 noobs; var variable estimate odds; run;
Variable Estimate odds
Intercept -1.9052 0.14880 Intercept -0.2216 0.80126 Intercept 1.5038 4.49880
An Example With Only Categorical Predictors
In SAS, a proportional odds model analysis can be performed using proc logistic with the option link = clogit. Here clogit stands for cumulative logit. In this example, we are going to use only categorical predictors, white (1=white 0=not white) and male (1=male 0=female), and we will focus more on the interpretation of the regression coefficients. Our model can be written as ) = αi + β1*white + β2*male, i = 1, 2, 3. The formula for the odds is shown in the table below. For example, we can see that the odds ratio for males versus females is exp(β2) and the odds ratio for the whites versus non-whites is exp(β1).
| Race Gender |
SD vs. all other choices |
SD and D vs. all other choices | SD, D and A vs. SA |
| White Male | exp(+ β1+ β2) | + β1+ β2) | + β1 + β2) |
| White Female | + β1) | + β1) | + β1) |
| Non-White Male | + β2) | + β2) | + β2) |
| None-White Female |
proc logistic data = ordwarm2 ; model warm = white male /link = clogit; run;
Response Profile
Ordered Total Value warm Frequency
1 1 297
2 2 723
3 3 856
4 4 417
Probabilities modeled are cumulated over the lower Ordered Values.
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 1 -2.5550 0.1277 400.0337 <.0001 Intercept 2 1 -0.8417 0.1159 52.7347 <.0001 Intercept 3 1 0.9326 0.1167 63.8455 <.0001 white 1 0.3422 0.1163 8.6594 0.0033 male 1 0.6450 0.0774 69.5178 <.0001
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits
white 1.408 1.121 1.769 male 1.906 1.638 2.218
From the output above, we can say that males have 1.906 times greater odds of somewhat disagreeing with the statement as females, no matter at what level.
A Example with a Continuous Predictor
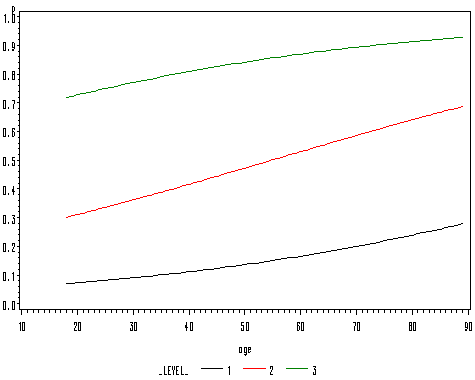
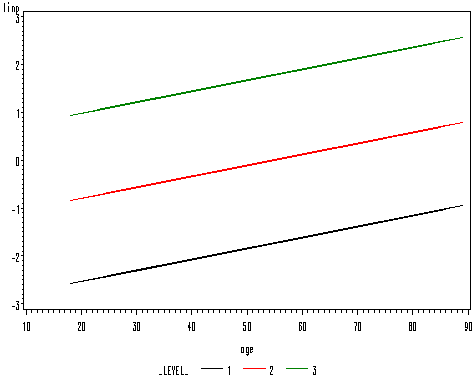
In this example, we are going to use a continuous predictor, age and show how to output the predicted values and how to graph them. The output statement below requests that SAS output predicted probabilities and the linear predictions and save them to a data set. Based on the proportionality assumption, we should expect that the lines for the linear predictions will be parallel to each other.
proc logistic data = ordwarm2 ; model warm = age /link = clogit; output out = pred p=p xbeta=linp; run;
proc sort data = pred; by age; run; goptions reset = all ; symbol i = join w=.4 ; proc gplot data = pred; plot p*age=_level_; plot linp*age=_level_; run; quit;
Another Example — Proportional Odds Assumption Test and Goodness of Fit
- Proportionality Assumption
In general, we can model the cumulative odds model in such as a way that each of the cumulative odds has its own regression model:
A proportional odds model simplifies the model so that the effects of the predictors are the same across different levels. This is the main assumption of the model. We need to test this assumption. That is, we need test the hypothesis that β1 = β2 = β3. SAS proc logistic performs a score test to test this hypothesis. Let’s look at the model with male and white as predictors again.
proc logistic data = ordwarm2 ; model warm = white male /link = clogit; run;
Score Test for the Proportional Odds Assumption
Chi-Square DF Pr > ChiSq 21.6592 4 0.0002
The p-value is really small, so we have to reject the null hypothesis of proportionality. The degrees of freedom is calculated as k*(r-2), where k is the number of predictors and r is the number of levels of response variables. In our example, we have two predictors and four levels of responses. It is not uncommon for a model not to satisfy the proportionality assumption (which is also called parallel regression assumption). When the test fails, other alternative models should be considered, such as multinomial logistic models.
- A Model with More Predictors
Now let’s take a look at a model where we use white, age and ed as our predictors. We also add options scale = none aggregate to get the goodness of fit tests. The deviance and Pearson tests compare the current model with the saturated model. This test being not significant tells us our model fits the data well.
proc logistic data = ordwarm2 ; model warm = white age ed /link = clogit scale=none aggregate; run;
Response Profile
Ordered Total Value warm Frequency
1 1 297
2 2 723
3 3 856
4 4 417
Probabilities modeled are cumulated over the lower Ordered Values.
Score Test for the Proportional Odds Assumption Chi-Square DF Pr > ChiSq 10.3962 6 0.1089
Deviance and Pearson Goodness-of-Fit Statistics
Criterion DF Value Value/DF Pr > ChiSq Deviance 2628 2523.3191 0.9602 0.9271 Pearson 2628 2588.2232 0.9849 0.7062
Number of unique profiles: 878
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 5997.541 5841.101 SC 6014.754 5875.526 -2 Log L 5991.541 5829.101
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 162.4403 3 <.0001
Score 157.6156 3 <.0001
Wald 157.7599 3 <.0001
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 1 -2.0393 0.2342 75.8321 <.0001 Intercept 2 1 -0.2698 0.2294 1.3829 0.2396 Intercept 3 1 1.5397 0.2318 44.1185 <.0001 white 1 0.4376 0.1176 13.8470 0.0002 age 1 0.0179 0.00241 54.8182 <.0001 ed 1 -0.0933 0.0129 52.6988 <.0001
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits
white 1.549 1.230 1.951 age 1.018 1.013 1.023 ed 0.911 0.888 0.934
Summary
This seminar illustrates how to perform binary logistic, exact logistic, multinomial logistic (generalized logits model) and ordinal logistic (proportional odds model) regression analysis using SAS proc logistic. It focuses on some new features of proc logistic available since SAS 8.1.
Some References:
Analysis of Categorical Dependent Variables with SAS and SPSS Performing Exact Logistic Regression with the SAS System SAS/STAT Software: Changes and Enhancements, Release 8.2