In previous sections we have shown how to estimate two types of measurement models, confirmatory factor models, and mixture models (e.g., latent class analysis). We have also shown how to estimate a path model, where relationships among observed variables are modeled. Structural equation models combine the two, using regression paths to estimate a model with a specific set of relationships among latent variables. Structural equation models typically imposes restrictions on the relationships between the latent variables, that is, only a subset of the possible paths between the latent variables are included.
Mplus version 5.2 was used for these examples.
1.0 A Structural Equation Model
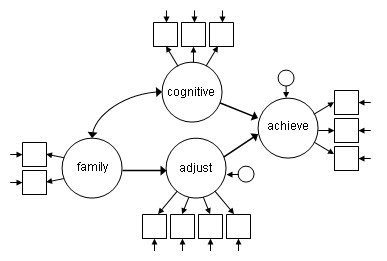
The following model continues from the example introduced in the confirmatory factor analysis page. The diagram below shows the model to be tested. Unlike a confirmatory factor analysis (CFA) model where all of the latent variables are allowed to covary, this model specifies a set of relationships among the latent variables some of these relationships are directional (i.e., regression paths) and some are not (i.e., covariances). The model also specifies that any covariance between cognitive and adjust is entirely through their relationships with other variables in the model.
In the model: command we use the keyword by to define the four latent variables as we did in the CFA. Below that the keyword on is used to specify that we want to predict achieve using cognitive and adjust (i.e., achieve on cog adjust;). The model also predicts adjust using family (adjust on family;). Notice that the model: command does not include a covariance between family and cognitive (i.e., family with cog;), although we could include this command, it is not necessary, as Mplus will include this covariance by default.
Title: A structural equation model Data: File is worland_data.dat ; Variable: Names are ppsych ses verbal vissp mem read arith spell motiv extra harm stabi; Model: family by ppsych ses; cog by verbal vissp mem; achieve by read arith spell; adjust by motiv extra harm stabi; achieve on cog adjust; adjust on family;
The abridged output for the above model is shown below.
<output omitted>
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 635.015
Degrees of Freedom 50
P-Value 0.0000
Chi-Square Test of Model Fit for the Baseline Model
Value 4124.707
Degrees of Freedom 66
P-Value 0.0000
CFI/TLI
CFI 0.856
TLI 0.810
Loglikelihood
H0 Value -6762.779
H1 Value -6445.272
Information Criteria
Number of Free Parameters 40
Akaike (AIC) 13605.559
Bayesian (BIC) 13774.143
Sample-Size Adjusted BIC 13647.180
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.153
90 Percent C.I. 0.142 0.164
Probability RMSEA <= .05 0.000
SRMR (Standardized Root Mean Square Residual)
Value 0.067
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
FAMILY BY
PPSYCH 1.000 0.000 999.000 999.000
SES -1.093 0.121 -9.055 0.000
COG BY
VERBAL 1.000 0.000 999.000 999.000
VISSP 0.844 0.045 18.772 0.000
MEM 0.969 0.044 21.798 0.000
ACHIEVE BY
READ 1.000 0.000 999.000 999.000
ARITH 0.836 0.034 24.715 0.000
SPELL 0.951 0.027 35.681 0.000
ADJUST BY
MOTIV 1.000 0.000 999.000 999.000
EXTRA 0.232 0.049 4.750 0.000
HARM 0.867 0.043 20.248 0.000
STABI 0.669 0.045 14.697 0.000
ACHIEVE ON
COG 0.892 0.050 17.692 0.000
ADJUST 0.139 0.040 3.485 0.000
ADJUST ON
FAMILY -1.183 0.135 -8.783 0.000
COG WITH
FAMILY -0.412 0.046 -9.019 0.000
Intercepts
PPSYCH 0.000 0.045 0.000 1.000
SES 0.000 0.045 0.000 1.000
VERBAL 0.000 0.045 0.000 1.000
VISSP 0.000 0.045 0.000 1.000
MEM 0.000 0.045 0.000 1.000
READ 0.000 0.045 0.000 1.000
ARITH 0.000 0.045 0.000 1.000
SPELL 0.000 0.045 0.000 1.000
MOTIV 0.000 0.045 0.000 1.000
EXTRA 0.000 0.045 0.000 1.000
HARM 0.000 0.045 0.000 1.000
STABI 0.000 0.045 0.000 1.000
Variances
FAMILY 0.252 0.049 5.119 0.000
COG 0.745 0.064 11.668 0.000
Residual Variances
PPSYCH 0.746 0.054 13.883 0.000
SES 0.697 0.052 13.467 0.000
VERBAL 0.253 0.025 10.255 0.000
VISSP 0.467 0.034 13.626 0.000
MEM 0.299 0.027 11.143 0.000
READ 0.096 0.014 6.855 0.000
ARITH 0.367 0.027 13.676 0.000
SPELL 0.183 0.016 11.458 0.000
MOTIV 0.107 0.032 3.346 0.001
EXTRA 0.950 0.061 15.700 0.000
HARM 0.328 0.033 10.039 0.000
STABI 0.600 0.042 14.252 0.000
ACHIEVE 0.170 0.022 7.845 0.000
ADJUST 0.539 0.053 10.170 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.316E-02
(ratio of smallest to largest eigenvalue)
In the output above in the MODEL RESULTS section, we first see the measurement portion of the model where the four latent variables are defined. The next section shows the structural portion of the model predicting achieve (ACHIEVE ON) and adjust (ADJUST ON). The coefficients shown under ACHIEVE ON are the coefficients from the latent variable achieve regressed on the latent variables cog and adjust, and can be interpreted as regression coefficients. The standard errors, the ratio of the coefficient to its standard error (i.e., a t- or z-value), and a p-value are also given for each structural coefficient. Below the regression results is the estimate of the covariance between the exogenous latent variables cog and family. The rest of the output is similar to the output for the measurement model except that rather than having a variance (listed under Variances) achieve and adjust now have residual variances (listed under Residual Variances) because they are being predicted by other variables in the model.
2.0 Including an Observed Variable in the Structural Model
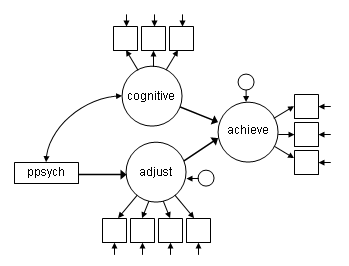
It is possible to include observed variables in the structural portion of the model. In the earlier models, the observed variables ses and ppsych, were used to estimate the latent variable family. In the current model the variable ses is removed from the model entirely, and the variable ppsych remains as a single observed variable predicting the latent variable adjust. The diagram below shows this model.
Removing ses from the model, and including ppsych as an observed variable requires three relatively small changes to the model. The first is that we have added the usevariables option in the variables: command, by default Mplus includes all variables in the dataset in the model. (Note that the names option tells Mplus the number, names, and order of the variables in the dataset, so we do not want to make any changes to it.) The usevariables option allows us to tell Mplus that we want to use a subset of the variables in our file. Since we only want to exclude ses, the usevariables option is followed by the names of all the variables in our dataset except ses. The second change is that we have removed the line in the model: command that was used to define the latent variable family because we no longer want to estimate that latent variable. The final change is that we now use ppsych to predict adjust (i.e., adjust on ppsych;)
Title: Adding an observed variable in the structural model; Data: File is worland_data.dat ; Variable: Names are ppsych ses verbal vissp mem read arith spell motiv extra harm stabi; Usevariables are ppsych verbal vissp mem read arith spell motiv extra harm stabi; Model: cog by verbal vissp mem; achieve by read arith spell; adjust by motiv extra harm stabi; achieve on cog adjust; adjust on ppsych;
The output for this model is shown below.
<output omitted>
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 729.459
Degrees of Freedom 41
P-Value 0.0000
Chi-Square Test of Model Fit for the Baseline Model
Value 3929.228
Degrees of Freedom 55
P-Value 0.0000
CFI/TLI
CFI 0.822
TLI 0.762
Loglikelihood
H0 Value -6198.772
H1 Value -5834.042
Information Criteria
Number of Free Parameters 34
Akaike (AIC) 12465.544
Bayesian (BIC) 12608.841
Sample-Size Adjusted BIC 12500.923
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.183
90 Percent C.I. 0.172 0.195
Probability RMSEA <= .05 0.000
SRMR (Standardized Root Mean Square Residual)
Value 0.153
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
COG BY
VERBAL 1.000 0.000 999.000 999.000
VISSP 0.865 0.046 18.821 0.000
MEM 0.963 0.046 20.863 0.000
ACHIEVE BY
READ 1.000 0.000 999.000 999.000
ARITH 0.836 0.034 24.686 0.000
SPELL 0.952 0.027 35.669 0.000
ADJUST BY
MOTIV 1.000 0.000 999.000 999.000
EXTRA 0.222 0.051 4.392 0.000
HARM 0.898 0.052 17.390 0.000
STABI 0.688 0.049 13.929 0.000
ACHIEVE ON
COG 0.859 0.046 18.691 0.000
ADJUST 0.216 0.035 6.116 0.000
ADJUST ON
PPSYCH -0.254 0.042 -6.008 0.000
PPSYCH WITH
COG -0.396 0.038 -10.362 0.000
Intercepts
VERBAL 0.000 0.041 0.000 1.000
VISSP 0.000 0.042 0.000 1.000
MEM 0.000 0.041 0.000 1.000
READ 0.000 0.038 0.000 1.000
ARITH 0.000 0.040 0.000 1.000
SPELL 0.000 0.039 0.000 1.000
MOTIV 0.000 0.043 0.000 1.000
EXTRA 0.000 0.045 0.000 1.000
HARM 0.000 0.043 0.000 1.000
STABI 0.000 0.044 0.000 1.000
Variances
COG 0.738 0.063 11.628 0.000
Residual Variances
VERBAL 0.260 0.026 9.912 0.000
VISSP 0.445 0.034 13.157 0.000
MEM 0.313 0.029 10.965 0.000
READ 0.097 0.014 6.852 0.000
ARITH 0.368 0.027 13.703 0.000
SPELL 0.181 0.016 11.385 0.000
MOTIV 0.136 0.041 3.323 0.001
EXTRA 0.955 0.061 15.671 0.000
HARM 0.303 0.039 7.826 0.000
STABI 0.589 0.043 13.851 0.000
ACHIEVE 0.170 0.022 7.740 0.000
ADJUST 0.798 0.070 11.388 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.145E-01
(ratio of smallest to largest eigenvalue)
The MODEL RESULTS section begins with the three (instead of four) latent variables in the model. In the structural (ON) portion of the output the coefficient for adjust regressed on ppsych is presented in the output the same way the coefficients for the latent predictor variables are reported. Below that, the covariance between ppsych and cog is shown under the heading PPSYCH WITH. The rest of the output is similar to the previous models.
You may have noticed that the mean and variance of ppsych are not included in the output, either on their own or as an intercept (mean) and residual variance. While Mplus estimates the covariance between the observed variable ppsych and the latent variable cog by default, it does not estimate the mean and variance of exogenous observed variables by default (the variances of latent exogenous variables are estimated by default). Explicitly including the covariance of ppsych and cog (ppsych with cog;), the mean of ppsych ([ppsych];), or the variance of ppsych (ppsych;) in the model: command will cause the mean and variance of ppsych to be estimated and included in the output. Note that the parameter estimates, as well as many fit indices (including the chi-square) and degrees of freedom will be the same with regardless of whether the mean and variance of ppsych are estimated, because the models are essentially the same. The one difference is that the the number of estimated parameters increases by two, this does not change the degrees of freedom though, because two additional pieces of information are included in the model which offsets the additional two parameters being estimated. Because the number of parameters being estimated changes, measures of model fit that are are calculated based on the number of estimated parameters, for example, AIC and BIC, will be different.
3.0 Additional Output
Above we have shown only the default output for each model, but a range of additional output can be requested using the Output: command. Below we show a few commonly used output options.
Sample Statistics
The input below is the same as the input for our first model except for the addition of the output: command. We use the sampstat; option to request that sample statistics (observed variable means, covariances and correlations) be included in the output.
Title:
Data:
File is worland_data.dat ;
Variable:
Names are
ppsych ses verbal vissp mem read arith spell motiv extra harm stabi;
Model:
family by ppsych ses;
cog by verbal vissp mem;
achieve by read arith spell;
adjust by motiv extra harm stabi;
achieve on cog adjust;
adjust on family;
Output:
sampstat;
Below we show the additional output provided by the sampstat; option (all other output has been omitted to save space). The "sample statistics" section shown below appears towards the top of the output file, after the "summary of analysis" and before the "tests of model fit".
SAMPLE STATISTICS
Means
PPSYCH SES VERBAL VISSP MEM
________ ________ ________ ________ ________
1 0.000 0.000 0.000 0.000 0.000
Means
READ ARITH SPELL MOTIV EXTRA
________ ________ ________ ________ ________
1 0.000 0.000 0.000 0.000 0.000
Means
HARM STABI
________ ________
1 0.000 0.000
Covariances
PPSYCH SES VERBAL VISSP MEM
________ ________ ________ ________ ________
PPSYCH 0.998
SES -0.419 0.998
VERBAL -0.429 0.499 0.998
VISSP -0.399 0.399 0.659 0.998
MEM -0.349 0.379 0.669 0.659 0.998
READ -0.389 0.429 0.778 0.559 0.729
ARITH -0.240 0.369 0.689 0.489 0.699
SPELL -0.309 0.329 0.629 0.479 0.719
MOTIV -0.250 0.249 0.489 0.319 0.579
EXTRA -0.140 0.170 0.180 0.090 0.170
HARM -0.249 0.259 0.419 0.249 0.459
STABI -0.160 0.180 0.329 0.269 0.349
Covariances
READ ARITH SPELL MOTIV EXTRA
________ ________ ________ ________ ________
READ 0.998
ARITH 0.729 0.998
SPELL 0.868 0.719 0.998
MOTIV 0.529 0.599 0.589 0.998
EXTRA 0.140 0.150 0.150 0.249 0.998
HARM 0.419 0.439 0.449 0.768 0.190
STABI 0.359 0.379 0.379 0.589 -0.289
Covariances
HARM STABI
________ ________
HARM 0.998
STABI 0.579 0.998
Correlations
PPSYCH SES VERBAL VISSP MEM
________ ________ ________ ________ ________
PPSYCH 1.000
SES -0.420 1.000
VERBAL -0.430 0.500 1.000
VISSP -0.400 0.400 0.660 1.000
MEM -0.350 0.380 0.670 0.660 1.000
READ -0.390 0.430 0.780 0.560 0.730
ARITH -0.240 0.370 0.690 0.490 0.700
SPELL -0.310 0.330 0.630 0.480 0.720
MOTIV -0.250 0.250 0.490 0.320 0.580
EXTRA -0.140 0.170 0.180 0.090 0.170
HARM -0.250 0.260 0.420 0.250 0.460
STABI -0.160 0.180 0.330 0.270 0.350
Correlations
READ ARITH SPELL MOTIV EXTRA
________ ________ ________ ________ ________
READ 1.000
ARITH 0.730 1.000
SPELL 0.870 0.720 1.000
MOTIV 0.530 0.600 0.590 1.000
EXTRA 0.140 0.150 0.150 0.250 1.000
HARM 0.420 0.440 0.450 0.770 0.190
STABI 0.360 0.380 0.380 0.590 -0.290
Correlations
HARM STABI
________ ________
HARM 1.000
STABI 0.580 1.000
Standardized Coefficients
Standardized coefficients, and, with some models, R2, can be obtained using the standardize option of the output: command. Mplus actually produces three forms of standardized coefficients, labeled, stdyx, stdy, and std. Using the standardize option requests all three, using these names as options one allows the user to request that only one (or two) sets of standardized estimates be printed. Below the output: command, is shown, the input file is otherwise unchanged.
Output: standardize;
or
Output: stdyx;
The abridged output (using standardize;) is shown below.
<output omitted>
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
FAMILY BY
PPSYCH 1.000 0.000 999.000 999.000
SES -1.093 0.121 -9.055 0.000
COG BY
VERBAL 1.000 0.000 999.000 999.000
VISSP 0.844 0.045 18.772 0.000
MEM 0.969 0.044 21.798 0.000
<output omitted>
STANDARDIZED MODEL RESULTS
STDYX Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
FAMILY BY
PPSYCH 0.502 0.042 11.913 0.000
SES -0.549 0.040 -13.780 0.000
COG BY
VERBAL 0.864 0.016 55.059 0.000
VISSP 0.729 0.024 30.279 0.000
MEM 0.837 0.018 47.624 0.000
ACHIEVE BY
READ 0.950 0.008 119.262 0.000
ARITH 0.795 0.019 42.875 0.000
SPELL 0.904 0.010 88.541 0.000
ADJUST BY
MOTIV 0.945 0.017 54.667 0.000
EXTRA 0.219 0.046 4.798 0.000
HARM 0.819 0.021 38.479 0.000
STABI 0.632 0.031 20.700 0.000
ACHIEVE ON
COG 0.811 0.032 25.571 0.000
ADJUST 0.138 0.040 3.454 0.001
ADJUST ON
FAMILY -0.629 0.036 -17.328 0.000
COG WITH
FAMILY -0.950 0.035 -26.824 0.000
Intercepts
PPSYCH 0.000 0.045 0.000 1.000
SES 0.000 0.045 0.000 1.000
VERBAL 0.000 0.045 0.000 1.000
VISSP 0.000 0.045 0.000 1.000
MEM 0.000 0.045 0.000 1.000
READ 0.000 0.045 0.000 1.000
ARITH 0.000 0.045 0.000 1.000
SPELL 0.000 0.045 0.000 1.000
MOTIV 0.000 0.045 0.000 1.000
EXTRA 0.000 0.045 0.000 1.000
HARM 0.000 0.045 0.000 1.000
STABI 0.000 0.045 0.000 1.000
Variances
FAMILY 1.000 0.000 999.000 999.000
COG 1.000 0.000 999.000 999.000
Residual Variances
PPSYCH 0.748 0.042 17.663 0.000
SES 0.698 0.044 15.959 0.000
VERBAL 0.253 0.027 9.331 0.000
VISSP 0.468 0.035 13.312 0.000
MEM 0.299 0.029 10.175 0.000
READ 0.097 0.015 6.385 0.000
ARITH 0.368 0.029 12.509 0.000
SPELL 0.183 0.018 9.929 0.000
MOTIV 0.107 0.033 3.289 0.001
EXTRA 0.952 0.020 47.669 0.000
HARM 0.328 0.035 9.410 0.000
STABI 0.601 0.039 15.588 0.000
ACHIEVE 0.189 0.025 7.645 0.000
ADJUST 0.605 0.046 13.249 0.000
STDY Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
FAMILY BY
PPSYCH 0.502 0.042 11.913 0.000
SES -0.549 0.040 -13.780 0.000
COG BY
VERBAL 0.864 0.016 55.059 0.000
VISSP 0.729 0.024 30.279 0.000
MEM 0.837 0.018 47.624 0.000
<output omitted>
STD Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
FAMILY BY
PPSYCH 0.502 0.049 10.238 0.000
SES -0.549 0.048 -11.423 0.000
COG BY
VERBAL 0.863 0.037 23.337 0.000
VISSP 0.729 0.040 18.177 0.000
MEM 0.836 0.038 22.142 0.000
<output omitted>
R-SQUARE
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value
PPSYCH 0.252 0.042 5.957 0.000
SES 0.302 0.044 6.890 0.000
VERBAL 0.747 0.027 27.529 0.000
VISSP 0.532 0.035 15.139 0.000
MEM 0.701 0.029 23.812 0.000
READ 0.903 0.015 59.631 0.000
ARITH 0.632 0.029 21.438 0.000
SPELL 0.817 0.018 44.271 0.000
MOTIV 0.893 0.033 27.333 0.000
EXTRA 0.048 0.020 2.399 0.016
HARM 0.672 0.035 19.240 0.000
STABI 0.399 0.039 10.350 0.000
Latent Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value
ACHIEVE 0.811 0.025 32.837 0.000
ADJUST 0.395 0.046 8.664 0.000
Modification Indices
It is necessary for every model makes certain assumptions, one common assumption is that a parameter is equal to a given value, often zero (e.g. saying there is no direct relationship between two variables). Modification indices can be used to help evaluate how reasonable these assumptions are by giving the researcher a sense of what happens when those assumptions are relaxed. Modification indices can be obtained using the modinces; option of the Output: command. Below we show only the Output: command, the input file remains otherwise unchanged. By default Mplus prints only those parameters with an MI greater than or equal to 10, other values can be requested by following the option name with a number in parentheses, for example, to get all parameters with an MI greater than or equal to 3.6, the option should read modindices(3.6);.
Output: modindices;
The modification indices are printed at the bottom of the output. The abridged output is shown below.
<output omitted>
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.316E-02
(ratio of smallest to largest eigenvalue)
MODEL MODIFICATION INDICES
NOTE: Modification indices for direct effects of observed dependent variables
regressed on covariates may not be included. To include these, request
MODINDICES (ALL).
Minimum M.I. value for printing the modification index 10.000
M.I. E.P.C. Std E.P.C. StdYX E.P.C.
BY Statements
FAMILY BY ARITH 25.687 -0.950 -0.476 -0.477
FAMILY BY SPELL 55.846 1.362 0.683 0.684
COG BY READ 12.217 0.389 0.336 0.337
COG BY ARITH 25.970 0.557 0.481 0.482
COG BY SPELL 60.405 -0.816 -0.704 -0.706
ACHIEVE BY PPSYCH 10.715 0.426 0.404 0.405
ACHIEVE BY VISSP 53.043 -0.863 -0.819 -0.820
ACHIEVE BY MEM 41.806 0.800 0.759 0.759
ADJUST BY VISSP 21.663 -0.230 -0.217 -0.217
ADJUST BY MEM 35.433 0.270 0.255 0.255
ADJUST BY READ 43.017 -0.225 -0.212 -0.213
ADJUST BY ARITH 30.444 0.236 0.223 0.223
ON/BY Statements
FAMILY ON ACHIEVE /
ACHIEVE BY FAMILY 15.997 0.389 0.735 0.735
FAMILY ON ADJUST /
ADJUST BY FAMILY 28.828 0.419 0.787 0.787
COG ON ACHIEVE /
ACHIEVE BY COG 16.642 0.715 0.786 0.786
COG ON ADJUST /
ADJUST BY COG 28.829 0.684 0.748 0.748
ACHIEVE ON FAMILY /
FAMILY BY ACHIEVE 10.038 2.206 1.166 1.166
ADJUST ON COG /
COG BY ADJUST 28.828 5.082 4.649 4.649
ADJUST ON ACHIEVE /
ACHIEVE BY ADJUST 36.036 5.334 5.362 5.362
WITH Statements
SES WITH PPSYCH 28.832 -0.208 -0.208 -0.289
VERBAL WITH SES 11.339 0.081 0.081 0.192
MEM WITH SES 10.444 -0.080 -0.080 -0.175
MEM WITH VERBAL 65.436 -0.185 -0.185 -0.675
MEM WITH VISSP 15.179 0.086 0.086 0.230
READ WITH VERBAL 48.870 0.088 0.088 0.564
READ WITH MEM 17.207 -0.054 -0.054 -0.316
ARITH WITH PPSYCH 16.778 0.103 0.103 0.197
ARITH WITH MEM 13.463 0.065 0.065 0.196
ARITH WITH READ 35.998 -0.100 -0.100 -0.531
SPELL WITH SES 12.813 -0.068 -0.068 -0.190
SPELL WITH VERBAL 60.337 -0.105 -0.105 -0.489
SPELL WITH MEM 26.201 0.072 0.072 0.307
SPELL WITH READ 44.080 0.143 0.143 1.080
MOTIV WITH SES 10.621 -0.074 -0.074 -0.272
MOTIV WITH MEM 19.099 0.069 0.069 0.385
MOTIV WITH READ 18.151 -0.048 -0.048 -0.475
MOTIV WITH ARITH 24.267 0.078 0.078 0.395
MOTIV WITH SPELL 12.809 0.044 0.044 0.317
EXTRA WITH MOTIV 33.374 0.158 0.158 0.494
HARM WITH MOTIV 11.320 -0.188 -0.188 -1.004
STABI WITH EXTRA 171.609 -0.458 -0.458 -0.606
STABI WITH HARM 20.922 0.132 0.132 0.298
ACHIEVE WITH FAMILY 10.039 0.054 0.261 0.261
ACHIEVE WITH COG 10.039 0.098 0.275 0.275
ADJUST WITH FAMILY 28.829 0.225 0.612 0.612
ADJUST WITH COG 28.829 0.369 0.582 0.582
ADJUST WITH ACHIEVE 10.028 1.004 3.317 3.317
Data Source
The data for these examples is based on a correlation matrix published in Worland et al. (1984). Although the correlation matrix would have been sufficient to specify these models, 500 cases were randomly drawn from the distribution described by the published correlation matrix. The models below do not necessarily match those specified in Worland et al. (1984), they are intended as examples only.
Worland, Julien, David G. Weeks, Cynthia L. Janes, and Barbara D. Strock (1984) Intelligence, classroom behavior, and academic achievement in children at high and low risk for psychopathology: A structural equation analysis. Journal of Abnormal Child Psychology Vol. 12, No. 3, pp. 437-454.