In this workshop, we will cover only some of what can be done with the PROCESS macro in SPSS. We will focus on mediation models. We will not cover moderation in any way. We will be using version 4.0 of the PROCESS macro. Much of the material in this workshop is based on Introduction to Mediation, Moderation and Conditional Process Analysis: A Regression-based Approach, Third Edition by Andrew F. Hayes (2022). The slides for this presentation are here.
Installing PROCESS
Let’s take a moment to look at the installation process. First, go to processmacro.org and then to the Downloads tab (at the top of the page). Download the zipped file, and then unzip the file. Next, read the Installing PROCESS custom dialog PDF. Finally, open and run the process.sps file. The custom dialog will remain installed as you open and close the SPSS program, but you must run the process.sps file each time you open SPSS and want to use the PROCESS macro. The instructions describe the installation process of the custom dialog based on the version of SPSS you are running; the execution of the process.sps file is the same in all versions of SPSS.
Simple mediation model with continuous predictor
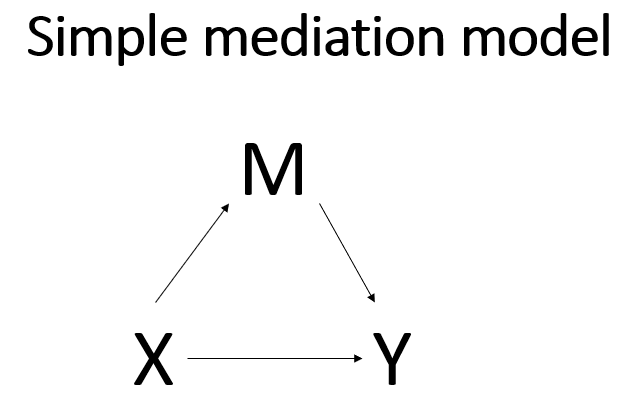
Like so much in statistics, the basics of mediation models depend on a good understanding of linear (OLS) regression. In a simple linear regression, we would have one continuous outcome and one predictor, perhaps a binary predictor or maybe a continuous predictor. The difference between a simple linear regression and a simple mediation analysis is the inclusion of a single (continuous) mediator to the model. Mathematically, the mediator acts like a covariate in the model. But conceptually, the mediator changes the simple regression model from a model that looks at the association of two variables to a model that tries to look at a causal relationship. Here is a conceptual diagram of a simple linear regression model:
We will assume that everyone is familiar linear regression.
In this model, we assume that there is a relationship between the predictor variable X and the outcome variable Y. The relationship may be correlational or causal or something else. There is no way to know the nature of the relationship from just the statistical model. The understanding of the relationship between X and Y comes from a thorough understanding of how the data were collected. In a simple mediation model, a third variable, called the mediator, M, is included in the model between X and Y.
The idea is that X now has two ways to influence Y. One way is direct, as in the simple regression model shown above. The second way is through M, the mediator. This is called the indirect effect. Of course, there is much more to mediation analysis than merely adding a variable to a regression model, and we will discuss some of those issues in this workshop. Because simple mediation analysis is based on linear regression, you can obtain much of the necessary output from a simple mediation analysis using a linear regression routine in your favorite statistical software program. However, other necessary parts of the output from a simple mediation analysis are difficult to get from regular regression output, so other routines are used. Some use structural equation modeling (SEM) routines. In this workshop, we will use a macro called PROCESS (version 4), which was written by Andrew F. Hayes. You can download this macro for free from processmacro.org . There are three versions of this macro: one for those who use SPSS, one for those who use SAS, and most recently, one for those who use R. Most of the documentation for the PROCESS macro can be found in Introduction to Mediation, Moderation and Conditional Process Analysis: A Regression-based Approach, Third Edition by Andrew F. Hayes (2022). Much of the content of this workshop is based on Part II of this book.
We will start off with the mechanics of how to run a simple mediation model, including the syntax for the PROCESS macro in SPSS. We will then discuss assumptions that we must test or explore in order to claim a causal relationship between the variables in the model. Finally, we will discuss models that have more than one mediator.
Let’s start with the simplest mediation model. This model has three continuous variables. Like a linear regression model, there is a predictor variable and an outcome variable. To make it a mediation model, we will add the mediator variable between the predictor and the outcome. The predictor variable (X) can be called the antecedent variable, because it occurs before either the mediator (M) or the outcome (Y). The outcome can be called the consequent variable, because it is believed to the consequence of the process the model describes. The mediator variable is both an antecedent variable (to the outcome) and a consequent variable (to the predictor).
The path from X to M is called a; the path from M to Y is called b; the path from X to Y is called c’. The indirect effect of X on Y through M is obtained by multiplying a and b. The total effect is the sum of the direct effect and the indirect effect. In other words, the total effect (called c) is (a * b) + c’. The fact that the indirect effect is obtained by multiplication has implications regarding the calculation of the standard error for this term.
For most of the tests given in the output of a mediation analysis, the normal theory approach is used. This approach makes some assumptions, and these assumptions are reasonable for these tests. However, there are at least two reasons to be concerned about using normal theory with indirect effects. First, it is known that the sampling distribution of a product term is (usually) not normal. Second, this approach may be lower in power than other approaches. There are several possible solutions for this, but the most commonly used solution is to calculate the confidence interval via bootstrap. In fact, bootstrapped confidence intervals are the default in PROCESS for the indirect effect.
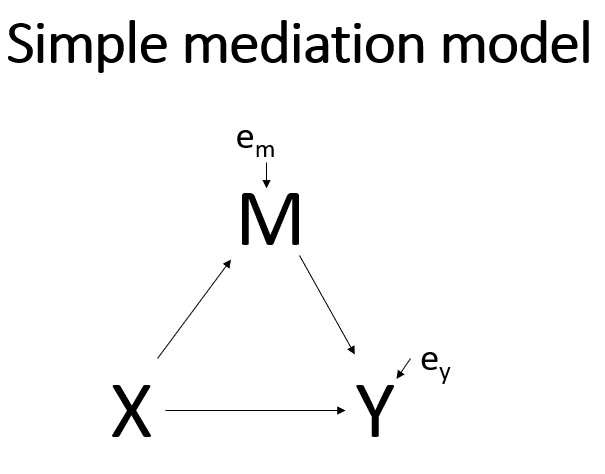
The diagram above is typically shown, but the diagram below is a little more accurate because it shows which variables have error terms associated with them.
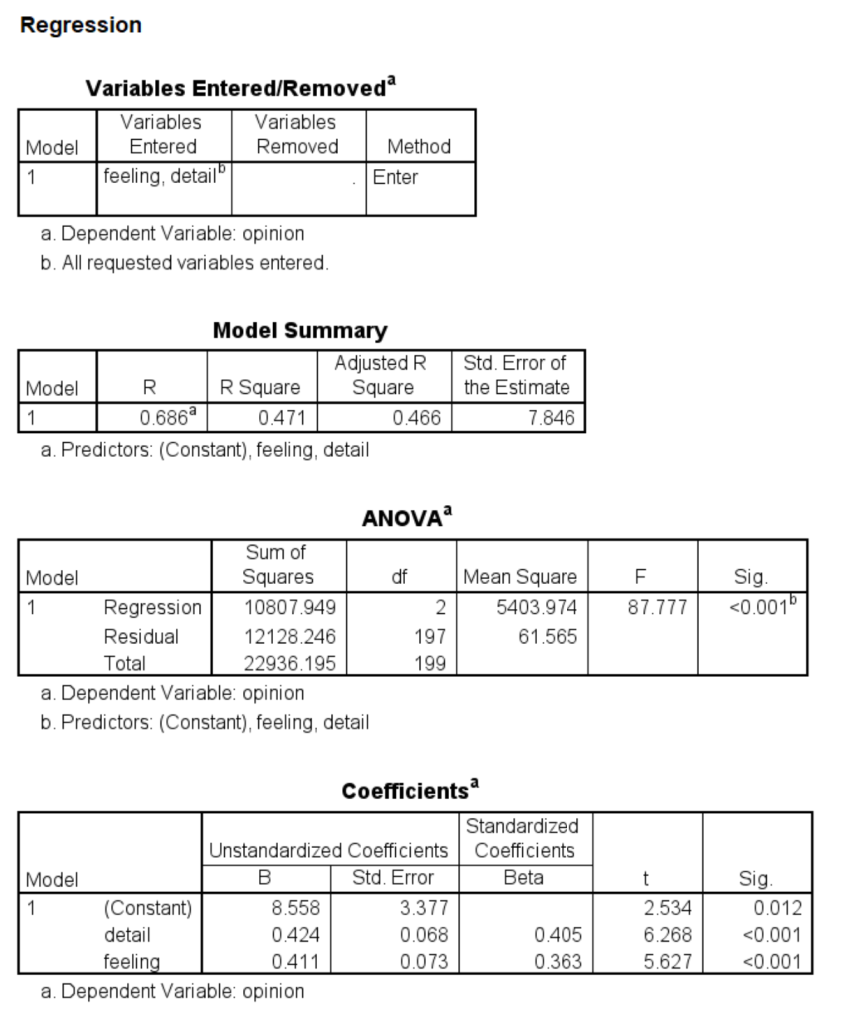
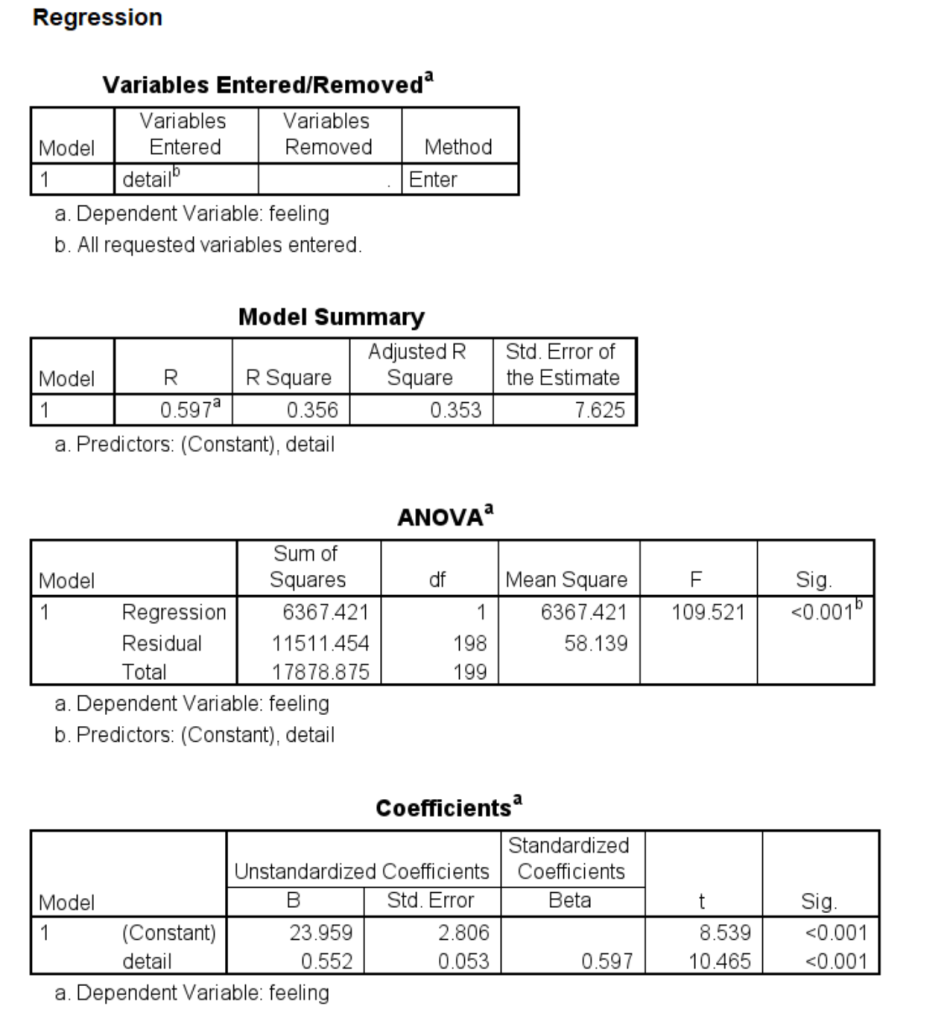
The outcome and mediator must be continuous when using the PROCESS macro; PROCESS checks for this and will not run if these variables are not continuous. The predictor may be continuous, binary or have multiple categories. In our first example, all of the variables in our simple mediation model will be continuous. We will use the hsbmediation data. This dataset contains 200 observations from a fictional study. In this fictional study, the researchers randomly assigned participants to receive information about senior living facilities. The amount of detail given to participants ranged from a little to quite a lot along a continuous scale. The variable is called detail in the dataset and is the predictor, or X, in the simple mediation model. The mediator (M) was a measure of feeling regarding senior living facilities (the variable feeling in the dataset), and the outcome (Y) was a measure of opinion strength regarding a proposed change to a law regarding senior living facilities (called opinion in the dataset).
If you want to run the model as two regressions, you could use this syntax:
regression dep = feeling /method = enter detail.
regression dep = opinion /method = enter detail feeling.
The PROCESS syntax looks like this:
process y = opinion /x = detail /m = feeling /model = 4/ seed = 30802022.
We give the name of the outcome variable on the y subcommand; the name of the predictor variable on the x subcommand, and the name of the mediator variable on the m subcommand. We must include the model number. The only place to get the model numbers is from Appendix A in Hayes’ book. We include the seed subcommand so that the results are exactly reproducible from one run to the next. Hayes recommends using the same seed for each analysis in your paper or research project.
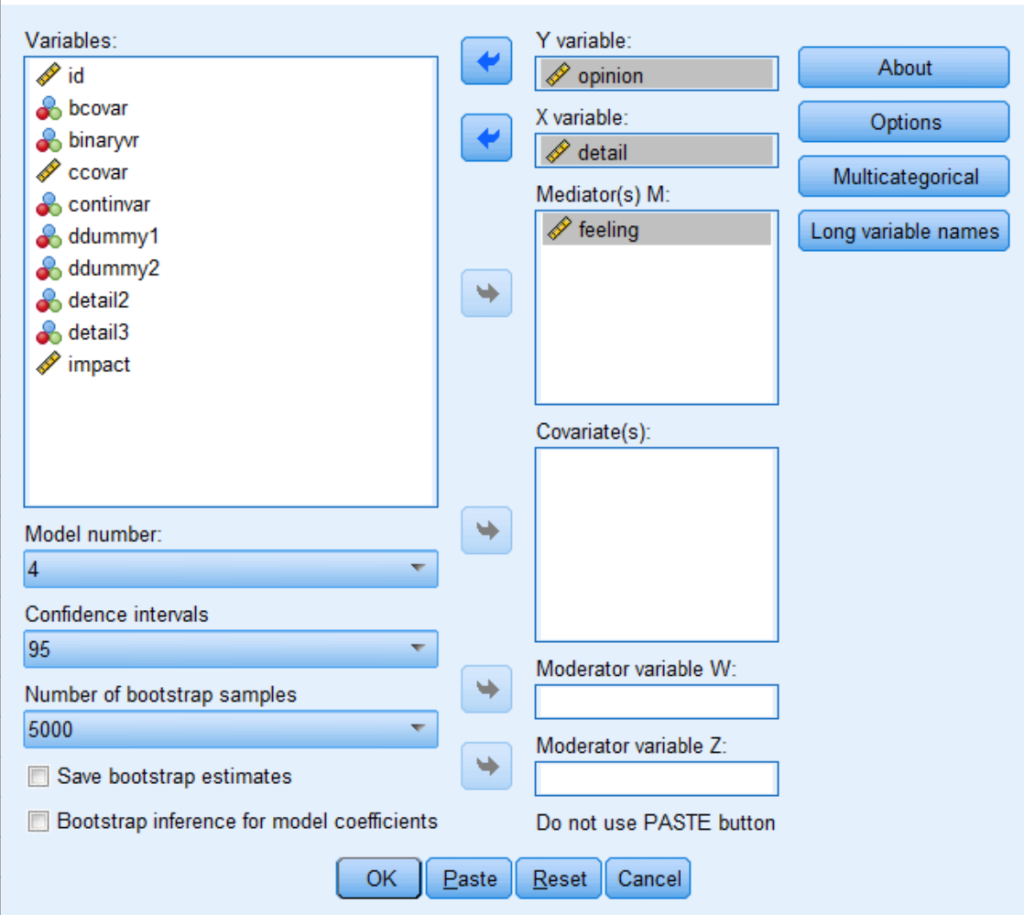
The point-and-click interface can also be used (if it has been installed). To access the dialog box, click on Analyze and then Regression and then PROCESS v4.0 by Andrew F. Hayes. Click the variables into the appropriate boxes so that it looks like this (do not forget to change the model number to 4).
The output is presented below. The output is the same whether syntax or point-and-click was used. We will go through each part of it now.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4 Part 1
Y : opinion
X : detail
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE: Part 2
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5968 .3561 58.1387 109.5213 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 23.9594 2.8057 8.5394 .0000 18.4265 29.4924
detail .5517 .0527 10.4652 .0000 .4477 .6557
**************************************************************************
OUTCOME VARIABLE: Part 3
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6865 .4712 61.5647 87.7772 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 8.5575 3.3773 2.5338 .0121 1.8972 15.2178
detail .4237 .0676 6.2676 .0000 .2904 .5571
feeling .4115 .0731 5.6265 .0000 .2673 .5557
****************** DIRECT AND INDIRECT EFFECTS OF X ON Y *****************
Direct effect of X on Y Part 4
Effect se t p LLCI ULCI
.4237 .0676 6.2676 .0000 .2904 .5571
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .2270 .0480 .1348 .3224
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output: Part 5
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
The first part of the output is important: It tells you what PROCESS used for the predictor, mediator and outcome, as well as the model number and number of observations used in the analysis. You should always check this first to ensure clear communication between you and PROCESS.
In part 2 of the output, the mediator is used as the outcome. There is only one predictor, which is the variable specified as X. The coefficient of the mediator on the predictor is the a path. It also matches the output from the first regression. A generic interpretation is that “… for two cases that are equal on M but differ by one unit on X, c’ is the estimated value of Y for the case with X = x minus the estimated value of Y for the case with X = x – 1.…the sign of c’ tells whether the case one unit higher on X is estimated to be higher (c’ = +) or lower (c’ = -) on Y. So a positive direct effect means that the case higher on X is estimated to be higher on Y, whereas a negative direct effect means that the case higher on X is estimated to be lower on Y. In the special case where X is dichotomous, with the two values of X differing by a single unit (e.g., X = 1 and X = 0), Y-hat can be interpreted as a group mean, …, meaning it estimates the difference between the two group means holding M constant. This is equivalent to what in analysis of covariance terms is called an adjusted mean difference” (page 85).
In part 3 of the output, Y is used as the outcome variable, and X and M are predictors. This output gives the b and c’ paths. It also matches the output from the second regression. The interpretation of b is the same as the interpretation of a, except that M is the antecedent instead of X, and Y is the outcome. “Two cases that differ by one unit on M but that are equal on X are estimated to differ by b units on Y” (page 86).
In part 4 of the output, we again see the total effect, along with the direct effect and the indirect effect. The total effect is 0.6508 = 0.4237 + 0.2270 (with a little rounding error). The indirect effect is simply a * b, or 0.5517*0.4115 = 0.2270. Notice that the CIs around this estimate are the bootstrapped CIs. Because they are bootstrapped CIs, the point estimate is not exactly in the center of the interval. Another definition of the indirect effect is ab = c – c’. “The indirect effect is the difference between the total effect of X on Y and the effect of X on Y controlling for M, the direct effect” (page 87).
Part 5 of the output of the output gives notes and errors. Of course, you want to review this section for anything problematic. The notes in this output give the level of confidence for all CIs presented in the output and the number of bootstrap samples for those CIs that were bootstrapped. In PROCESS, the default number of bootstrap samples is 5000. This can be changed, usually to a higher number.
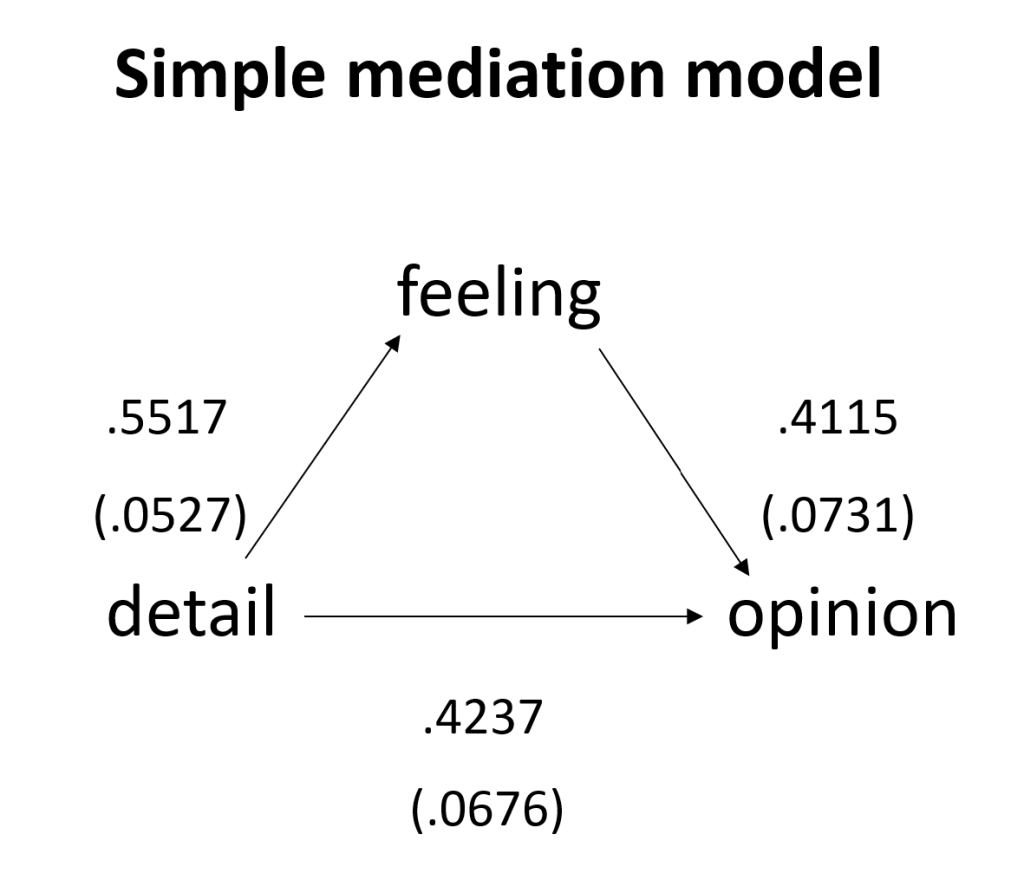
Making a diagram of the path model with the coefficients and standard errors is a good way to present the results. For this model, we might create something like:
Let’s confirm the calculations of the indirect and total effects. The indirect effect is the coefficient of the a path multiplied by the coefficient of the b path:0.5517*0.4115 = 0.2270 (which is what we see in the output). The total effect is the sum of direct effect and the indirect effect: 0.4237 + 0.2270 = 0.6507 (with a little rounding error). We do not see the total effect in the output above, but we probably want to include that. While it is easy enough to add the two numbers to get the total effect, we would like PROCESS to calculate the standard errors for us.
Adding Options
The total option
The total = 1 optional subcommand can be used to get additional information about the total effect.
process y = opinion /x = detail /m = feeling /model = 4 /total = 1 /seed = 30802022.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5968 .3561 58.1387 109.5213 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 23.9594 2.8057 8.5394 .0000 18.4265 29.4924
detail .5517 .0527 10.4652 .0000 .4477 .6557
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6865 .4712 61.5647 87.7772 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 8.5575 3.3773 2.5338 .0121 1.8972 15.2178
detail .4237 .0676 6.2676 .0000 .2904 .5571
feeling .4115 .0731 5.6265 .0000 .2673 .5557
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6215 .3862 71.0973 124.6031 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 18.4162 3.1027 5.9355 .0000 12.2976 24.5348
detail .6508 .0583 11.1626 .0000 .5358 .7657
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se t p LLCI ULCI
.6508 .0583 11.1626 .0000 .5358 .7657
Direct effect of X on Y
Effect se t p LLCI ULCI
.4237 .0676 6.2676 .0000 .2904 .5571
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .2270 .0480 .1348 .3224
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
The boot option
The boot = XXX optional subcommand can be used to change the number of bootstrapped samples used to calculate the standard error and confidence interval. Replace “XXX” with the desired number of samples. The default is 5000. In the example below, 10000 bootstrapped samples are requested.
process y = opinion /x = detail /m = feeling /model = 4 /boot = 10000 /seed = 30802022.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5968 .3561 58.1387 109.5213 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 23.9594 2.8057 8.5394 .0000 18.4265 29.4924
detail .5517 .0527 10.4652 .0000 .4477 .6557
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6865 .4712 61.5647 87.7772 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 8.5575 3.3773 2.5338 .0121 1.8972 15.2178
detail .4237 .0676 6.2676 .0000 .2904 .5571
feeling .4115 .0731 5.6265 .0000 .2673 .5557
****************** DIRECT AND INDIRECT EFFECTS OF X ON Y *****************
Direct effect of X on Y
Effect se t p LLCI ULCI
.4237 .0676 6.2676 .0000 .2904 .5571
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .2270 .0479 .1361 .3242
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
10000
------ END MATRIX -----
The stand option (AKA the scaling of the results)
Should the results be presented in the original metric of the variables used in the model, or should the coefficients be standardized? The answer is it depends: do you want to express the results in the original metrics of the variables, or do you want to express the results in terms of standard deviations? If the original metrics of the variables are meaningful, then there may be no need to standardize the results. If the metrics of the variables are arbitrary, then perhaps standardizing is a good idea. The results can be standardized without standardizing the variable before running the model, just as coefficients from a linear regression can be standardized without first standardizing the variables. When using the PROCESS macro, you can add the stand = 1 optional subcommand to get standardized coefficients.
process y = opinion /x = detail /m = feeling /total = 1/ model = 4/ seed = 30802022 /stand = 1.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5968 .3561 58.1387 109.5213 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 23.9594 2.8057 8.5394 .0000 18.4265 29.4924
detail .5517 .0527 10.4652 .0000 .4477 .6557
Standardized coefficients
coeff
detail .5968
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6865 .4712 61.5647 87.7772 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 8.5575 3.3773 2.5338 .0121 1.8972 15.2178
detail .4237 .0676 6.2676 .0000 .2904 .5571
feeling .4115 .0731 5.6265 .0000 .2673 .5557
Standardized coefficients
coeff
detail .4047
feeling .3633
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6215 .3862 71.0973 124.6031 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 18.4162 3.1027 5.9355 .0000 12.2976 24.5348
detail .6508 .0583 11.1626 .0000 .5358 .7657
Standardized coefficients
coeff
detail .6215
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se t p LLCI ULCI c_cs
.6508 .0583 11.1626 .0000 .5358 .7657 .6215
Direct effect of X on Y
Effect se t p LLCI ULCI c'_cs
.4237 .0676 6.2676 .0000 .2904 .5571 .4047
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .2270 .0480 .1348 .3224
Completely standardized indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .2168 .0432 .1302 .3016
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
Hayes is careful to note that fully standardized results make sense only when all of the variables in the model are continuous. He warns against standardizing the coefficients of binary predictors, as this may not make much sense substantively. In fact, if you request standardized coefficients and have specified a binary predictor variable (X), you will get only partially standardized results. A note to this effect will be given in the final part of the output. We will see an example of this in the next section.
The decimals option
The decimals optional subcommand can be added to alter the number of decimal places shown in the output. In the example below, the default number of decimal places is changed from four to two. Notice that the this change is using the type of format notation that would be used in SPSS to change the format of a numeric variable.
process y = opinion /x = detail /m = feeling /model = 4 /seed = 30802022 /decimals = f10.2.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.60 .36 58.14 109.52 1.00 198.00 .00
Model
coeff se t p LLCI ULCI
constant 23.96 2.81 8.54 .00 18.43 29.49
detail .55 .05 10.47 .00 .45 .66
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.69 .47 61.56 87.78 2.00 197.00 .00
Model
coeff se t p LLCI ULCI
constant 8.56 3.38 2.53 .01 1.90 15.22
detail .42 .07 6.27 .00 .29 .56
feeling .41 .07 5.63 .00 .27 .56
****************** DIRECT AND INDIRECT EFFECTS OF X ON Y *****************
Direct effect of X on Y
Effect se t p LLCI ULCI
.42 .07 6.27 .00 .29 .56
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .23 .05 .13 .32
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
Simple mediation model with binary predictor
Let’s modify this example just a little by using a binary predictor (X) instead of a continuous predictor. As you might expect, the syntax and interpretation will be the same.
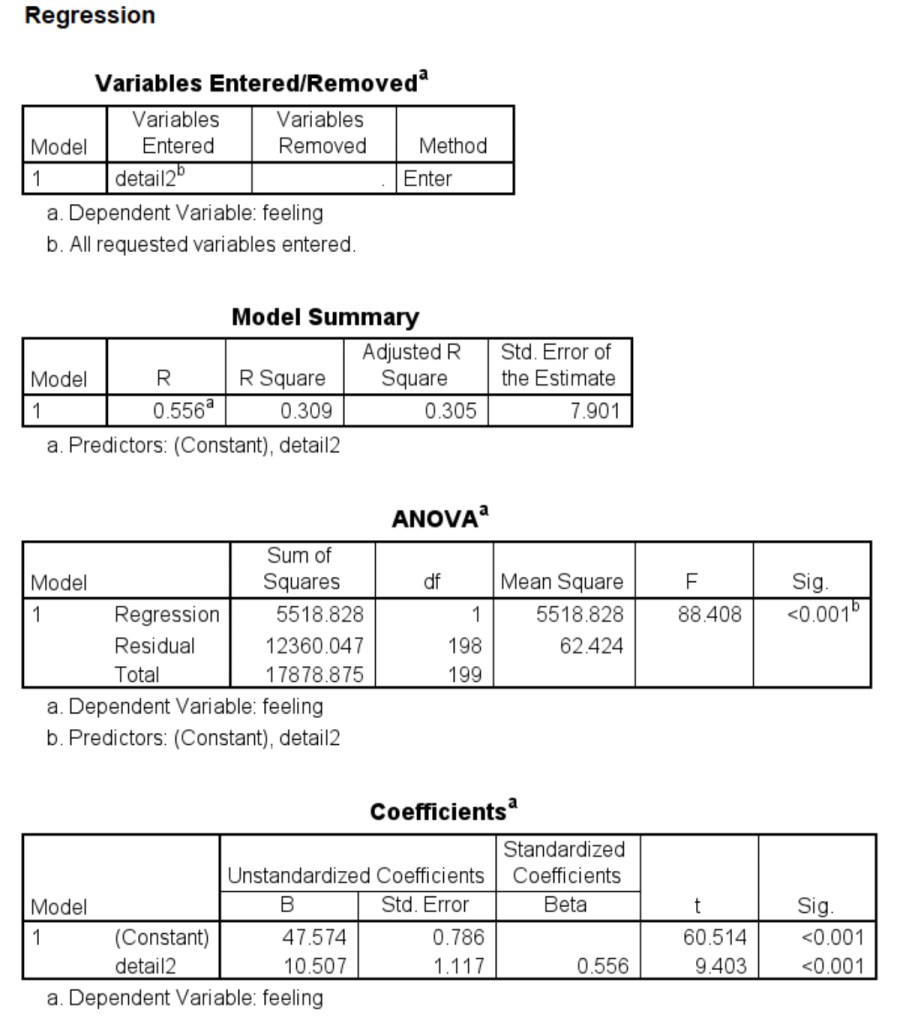
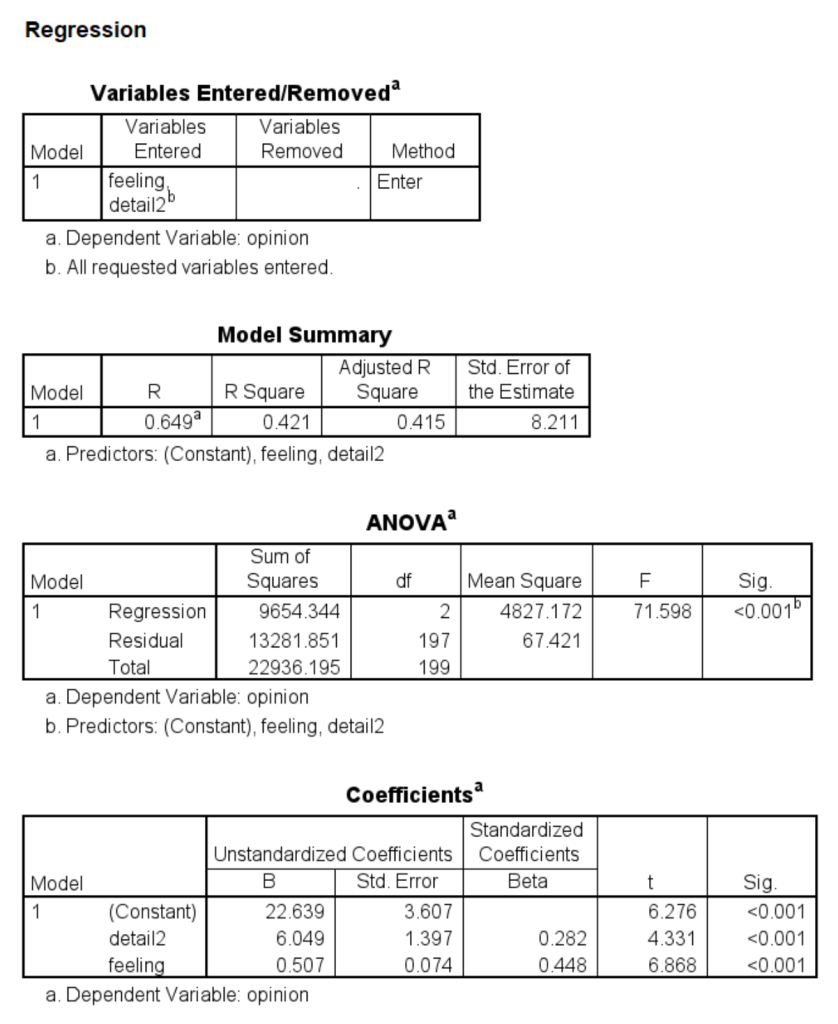
regression dep = feeling /method = enter detail2.
regression dep = opinion /method = enter detail2 feeling.
process y = opinion /x = detail2 /m = feeling /model = 4 /total = 1 /seed = 30802022.
Run MATRIX procedure:
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail2
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5556 .3087 62.4245 88.4081 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 47.5743 .7862 60.5139 .0000 46.0239 49.1246
detail2 10.5066 1.1174 9.4026 .0000 8.3030 12.7101
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6488 .4209 67.4206 71.5979 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 22.6388 3.6074 6.2757 .0000 15.5248 29.7529
detail2 6.0495 1.3967 4.3314 .0000 3.2951 8.8038
feeling .5073 .0739 6.8685 .0000 .3616 .6529
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.5313 .2822 83.1439 77.8615 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 46.7723 .9073 51.5506 .0000 44.9831 48.5615
detail2 11.3792 1.2896 8.8239 .0000 8.8361 13.9223
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se t p LLCI ULCI
11.3792 1.2896 8.8239 .0000 8.8361 13.9223
Direct effect of X on Y
Effect se t p LLCI ULCI
6.0495 1.3967 4.3314 .0000 3.2951 8.8038
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling 5.3298 1.0324 3.4409 7.4931
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
The interpretation of the results is the same as above. As stated on page 85, “In the special case where X is dichotomous, with the two values of X differing by a single unit (e.g., X = 1 and X = 0), Ŷ can be interpreted as a group mean, …, meaning c’ estimates the difference between the two group means holding M constant. This is equivalent to what in analysis of covariance terms is called an adjusted mean difference.”
Let’s add the stand = 1 optional subcommand to get standardized results and see what happens.
process y = opinion /x = detail2 /m = feeling / model = 4 /total = 1 /seed = 30802022 /stand = 1.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail2
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5556 .3087 62.4245 88.4081 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 47.5743 .7862 60.5139 .0000 46.0239 49.1246
detail2 10.5066 1.1174 9.4026 .0000 8.3030 12.7101
Standardized coefficients
coeff
detail2 1.1085
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6488 .4209 67.4206 71.5979 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 22.6388 3.6074 6.2757 .0000 15.5248 29.7529
detail2 6.0495 1.3967 4.3314 .0000 3.2951 8.8038
feeling .5073 .0739 6.8685 .0000 .3616 .6529
Standardized coefficients
coeff
detail2 .5635
feeling .4479
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.5313 .2822 83.1439 77.8615 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 46.7723 .9073 51.5506 .0000 44.9831 48.5615
detail2 11.3792 1.2896 8.8239 .0000 8.8361 13.9223
Standardized coefficients
coeff
detail2 1.0599
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se t p LLCI ULCI c_ps
11.3792 1.2896 8.8239 .0000 8.8361 13.9223 1.0599
Direct effect of X on Y
Effect se t p LLCI ULCI c'_ps
6.0495 1.3967 4.3314 .0000 3.2951 8.8038 .5635
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling 5.3298 1.0324 3.4409 7.4931
Partially standardized indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .4964 .0893 .3305 .6767
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
NOTE: Standardized coefficients for dichotomous or multicategorical X are in
partially standardized form.
------ END MATRIX -----
Simple mediation model with multicategorical predictor
Now let’s try using a predictor (X) that has three levels. It does not matter if the predictor variable is ordinal (has ordered categories) or if it is nominal, just as it does not matter in regression analysis. What does matter is how you code the categories. PROCESS offers a few different ways to code the categories of the predictor variable. Because indicator (AKA dummy) coding is so frequently used, we will use it in this example. PROCESS will make the dummy variables for you (but not add them to your dataset), so you do not need to create new variables before running this analysis. We will use the lowest-numbered category as our reference group. (Please see Regression for SPSS Chapter 5: Additional coding systems for categorical variables in regression analysis for more information on different types of coding systems.) In the syntax for PROCESS, the mcx = 1 optional subcommand is included to tell PROCESS that the predictor (X) has more than two categories and to use indicator (AKA dummy) coding. Unlike with the regression command in SPSS, we do not need to create the dummy variables before using PROCESS; PROCESS will do that for us (but the dummy variables are not added to the dataset, just as they are not when using the SPSS glm command).
PROCESS offers four different types of coding for categorical predictors; they are discussed below.
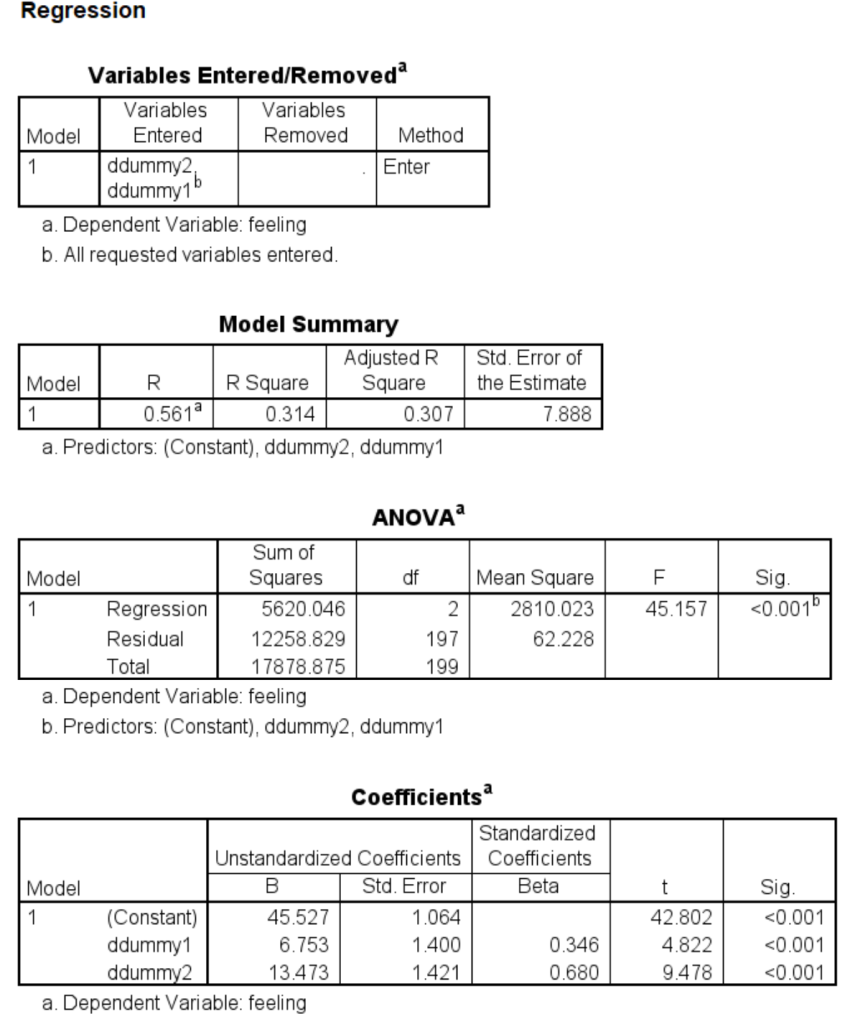
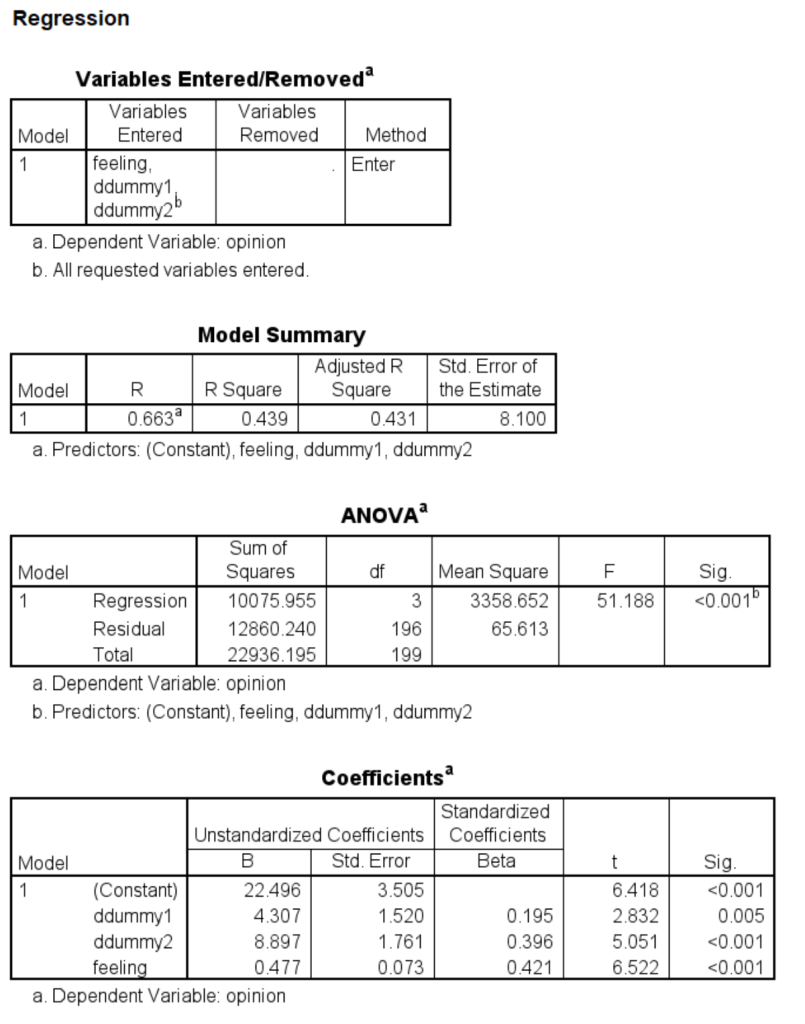
regression dep = feeling /method = enter ddummy1 ddummy2.
regression dep = opinion /method = enter ddummy1 ddummy2 feeling.
process y = opinion /x = detail3 /m = feeling /mcx = 1 /model = 4 /total = 1 /seed = 30802022.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4 Part 1
Y : opinion
X : detail3
M : feeling
Sample
Size: 200
Custom
Seed: 30802022
Coding of categorical X variable for analysis:
detail3 X1 X2
.000 .000 .000
1.000 1.000 .000
2.000 .000 1.000
**************************************************************************
OUTCOME VARIABLE: Part 2
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5607 .3143 62.2276 45.1572 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 45.5273 1.0637 42.8018 .0000 43.4296 47.6249
X1 6.7527 1.4004 4.8220 .0000 3.9910 9.5144
X2 13.4727 1.4214 9.4785 .0000 10.6696 16.2758
**************************************************************************
OUTCOME VARIABLE: Part 3
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6628 .4393 65.6135 51.1884 3.0000 196.0000 .0000
Model
coeff se t p LLCI ULCI
constant 22.4960 3.5053 6.4178 .0000 15.5831 29.4089
X1 4.3066 1.5205 2.8324 .0051 1.3080 7.3052
X2 8.8965 1.7612 5.0514 .0000 5.4232 12.3698
feeling .4771 .0732 6.5217 .0000 .3328 .6214
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE: Part 4
opinion
Model Summary
R R-sq MSE F df1 df2 p
.5636 .3176 79.4464 45.8501 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 44.2182 1.2019 36.7913 .0000 41.8480 46.5884
X1 7.5285 1.5823 4.7579 .0000 4.4080 10.6490
X2 15.3247 1.6061 9.5418 .0000 12.1574 18.4920
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Relative total effects of X on Y: Part 5
Effect se t p LLCI ULCI
X1 7.5285 1.5823 4.7579 .0000 4.4080 10.6490
X2 15.3247 1.6061 9.5418 .0000 12.1574 18.4920
Omnibus test of total effect of X on Y:
R2-chng F df1 df2 p
.3176 45.8501 2.0000 197.0000 .0000
----------
Relative direct effects of X on Y
Effect se t p LLCI ULCI
X1 4.3066 1.5205 2.8324 .0051 1.3080 7.3052
X2 8.8965 1.7612 5.0514 .0000 5.4232 12.3698
Omnibus test of direct effect of X on Y:
R2-chng F df1 df2 p
.0735 12.8516 2.0000 196.0000 .0000
----------
Relative indirect effects of X on Y
detail3 -> feeling -> opinion
Effect BootSE BootLLCI BootULCI
X1 3.2219 .8230 1.7287 4.9461
X2 6.4282 1.1885 4.1162 8.8586
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output: Part 6
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
Let’s put the coefficients and their standard errors on a diagram and then discuss the interpretation of the results.
Relative effects
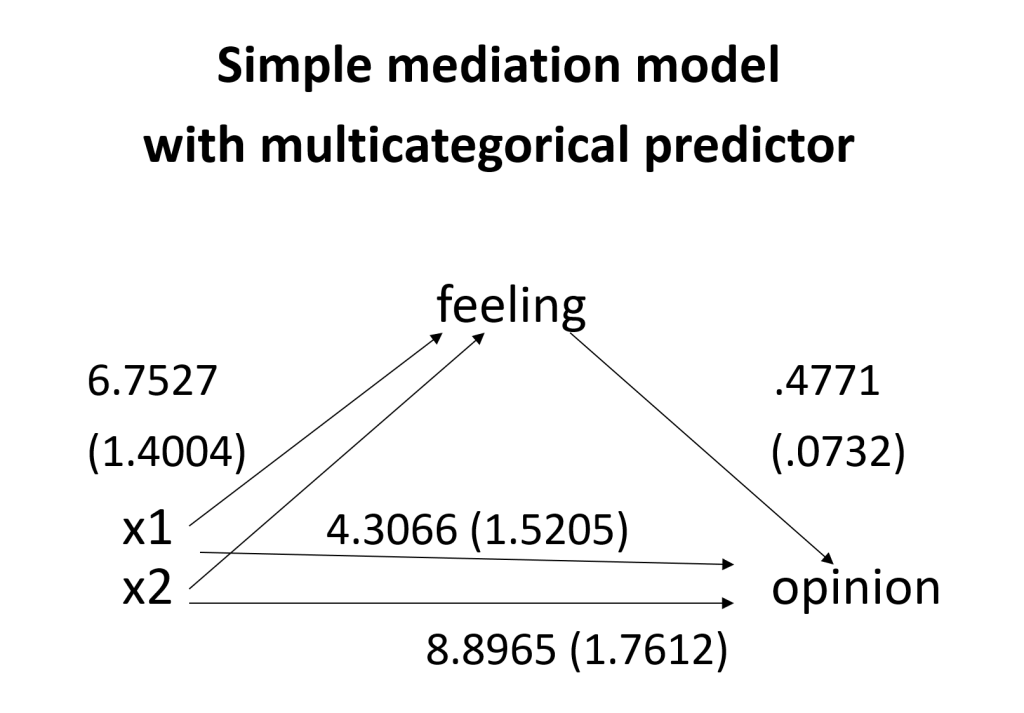
When there is more than one arrow from X to M, we now have relative effects. As in regression, we have coefficients for all but one of the categories of X. In this example, we used indicator (AKA dummy) coding. This is coding system is the one most commonly used with regression. The output shows the relative direct effects on X, the relative indirect effects on X, and the relative total effects on X. When interpreting relative effects, you need to remember which group (or category or level) of X is the reference group. In the example above, detail3 (X) is coded as 0, 1 and 2, with the group coded as 0 used as the reference group. The path for a1 is the mean of M1 – the mean of M0; the path for a2 is the mean of M2 – the mean of M0. The interpretation of the single coefficient from M to Y does not change even though there are multiple paths from X to M. Part 5 of the output gives the relative direct, relative indirect and relative total effects. Omnibus (AKA multi-degree-of-freedom) tests of these effects are also provided. These omnibus tests are used to determine if the overall effect is statistically significant.
PROCESS has four choices for coding systems: indicator (AKA dummy) (mcx = 1), sequential (mcx = 2), Helmert (mcx = 3) and effect coding (mcx = 4). You should choose which coding system to use based on the comparisons you wish to make. As in regression, the omnibus test will be the same regardless of which coding system you use, but the values of the coefficients will be different, and the associated p-values may be different as well (meaning that a coefficient may be statistically significant using one coding system and not statistically significant using a different coding system).
Let’s calculate the relative indirect effects and the relative total effects by hand. For the a1 path, 6.7527*0.4771 = 3.2217 (with rounding error). For the a2 path, 13.4727*0.4771 = 6.4278 (with rounding error). For the relative total effects, for the a1 path, we have 3.2217 + 4.3066 = 7.5283 (with rounding error). For the a2 path, we have 6.4278 + 8.8965 = 15.3243 (with rounding error).
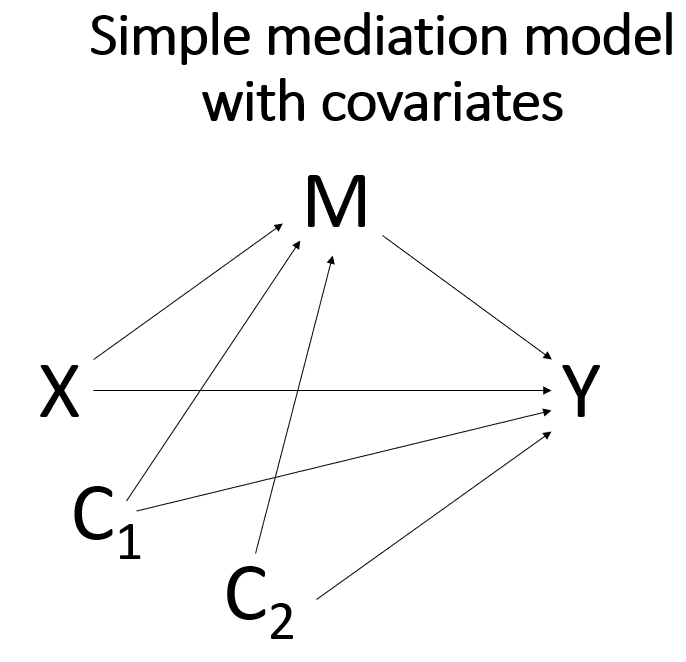
Simple mediation model with covariates
Covariates can be added to any mediation model. The covariates can be either continuous or binary. In the example below, we include two covariates, one continuous (the variable ccovar) and one binary (the variable bcovar). Notice that both covariates are added to both equations. This is necessary for the direct effect and indirect effect(s) to sum to the total effect.
Here is the diagram of the model.
process y = opinion /x = detail /m = feeling /model = 4 /total = 1 /cov = bcovar ccovar /seed = 30802022.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail
M : feeling
Covariates:
bcovar ccovar
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.7253 .5261 43.2323 72.5180 3.0000 196.0000 .0000
Model
coeff se t p LLCI ULCI
constant 11.8957 2.8628 4.1552 .0000 6.2497 17.5416
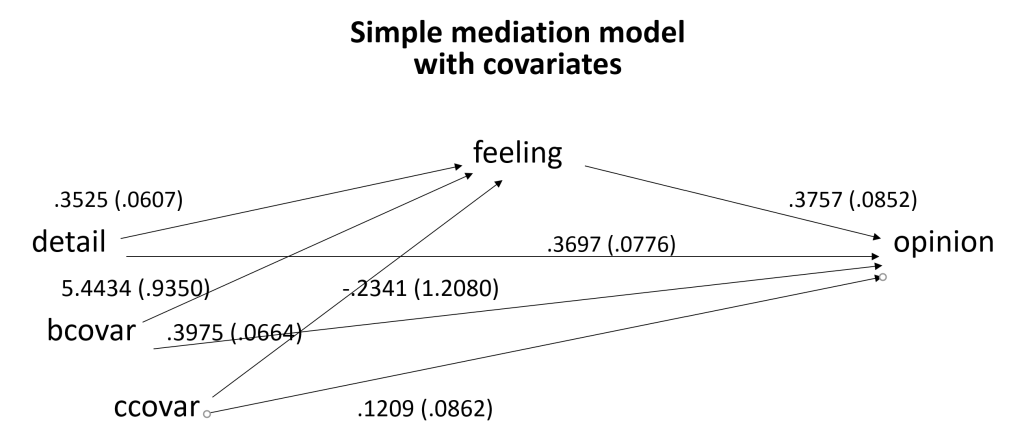
detail .3252 .0607 5.3551 .0000 .2055 .4450
bcovar 5.4434 .9350 5.8218 .0000 3.5994 7.2873
ccovar .3975 .0664 5.9858 .0000 .2665 .5284
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6906 .4769 61.5242 44.4499 4.0000 195.0000 .0000
Model
coeff se t p LLCI ULCI
constant 7.0291 3.5625 1.9731 .0499 .0032 14.0550
detail .3697 .0776 4.7656 .0000 .2167 .5227
feeling .3757 .0852 4.4097 .0000 .2077 .5438
bcovar -.2341 1.2080 -.1938 .8466 -2.6165 2.1484
ccovar .1209 .0862 1.4033 .1621 -.0490 .2908
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6517 .4248 67.3141 48.2446 3.0000 196.0000 .0000
Model
coeff se t p LLCI ULCI
constant 11.4989 3.5723 3.2189 .0015 4.4538 18.5439
detail .4919 .0758 6.4906 .0000 .3424 .6414
bcovar 1.8113 1.1667 1.5525 .1222 -.4896 4.1122
ccovar .2703 .0829 3.2616 .0013 .1068 .4337
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se t p LLCI ULCI
.4919 .0758 6.4906 .0000 .3424 .6414
Direct effect of X on Y
Effect se t p LLCI ULCI
.3697 .0776 4.7656 .0000 .2167 .5227
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .1222 .0356 .0580 .1965
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
The interpretation of the path coefficients is just the same as before, except that we now add “holding the covariates constant” to the discussion of the path coefficients. Below is the diagram with the coefficients and standard errors.
Simple mediation with covariates with robust standard errors
In the following example, we request robust standard errors. Robust standard errors often used when there is a question about meeting the assumption of homogeneity of variance. However, some authors use them in all analyses, just assuming that there are always at least minor violations of homogeneity of variance. There are five different types of robust standard errors available, and they are numbered from 0 to 4. (Definitions of these options are given in later section.) We use 4 in this example, but if you try it with other types of robust standard errors, you will likely see only a small change in the standard errors.
process y = opinion /x = detail /m = feeling /model = 4 /total = 1 /cov = bcovar ccovar /seed = 30802022 /hc = 4.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail
M : feeling
Covariates:
bcovar ccovar
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.7253 .5261 43.2323 97.9149 3.0000 196.0000 .0000
Model
coeff se(HC4) t p LLCI ULCI
constant 11.8957 2.5967 4.5811 .0000 6.7746 17.0167
detail .3252 .0593 5.4824 .0000 .2082 .4422
bcovar 5.4434 .9501 5.7293 .0000 3.5696 7.3171
ccovar .3975 .0641 6.1967 .0000 .2710 .5240
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.6906 .4769 61.5242 53.9715 4.0000 195.0000 .0000
Model
coeff se(HC4) t p LLCI ULCI
constant 7.0291 3.4393 2.0437 .0423 .2460 13.8122
detail .3697 .0761 4.8583 .0000 .2196 .5198
feeling .3757 .0909 4.1347 .0001 .1965 .5550
bcovar -.2341 1.1511 -.2033 .8391 -2.5043 2.0362
ccovar .1209 .0926 1.3052 .1934 -.0618 .3036
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.6517 .4248 67.3141 57.9148 3.0000 196.0000 .0000
Model
coeff se(HC4) t p LLCI ULCI
constant 11.4989 3.5004 3.2850 .0012 4.5956 18.4021
detail .4919 .0752 6.5396 .0000 .3436 .6402
bcovar 1.8113 1.1894 1.5228 .1294 -.5345 4.1571
ccovar .2703 .0838 3.2255 .0015 .1050 .4355
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se(HC4) t p LLCI ULCI
.4919 .0752 6.5396 .0000 .3436 .6402
Direct effect of X on Y
Effect se(HC4) t p LLCI ULCI
.3697 .0761 4.8583 .0000 .2196 .5198
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
feeling .1222 .0356 .0580 .1965
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
NOTE: A heteroscedasticity consistent standard error and covariance matrix estimator was used.
------ END MATRIX -----
Multiple predictor variables
The PROCESS macro only allows for a single predictor variable. However, sometimes you may want to have two or more predictor variables in your mediation model. This can be done in PROCESS with a little “trick”. The “trick” is to include the additional predictor variables as covariates. This may seem strange at first, but remember that predictors and covariates are the same thing (i.e., independent variables) in regression models. It is the same idea here. Should you run separate models for each predictor, or should you run a single that includes all of the predictors? The answer to that question depends on each individual research situation. Considerations include the research question to be addressed, the sample size, the number of tests that will results from each option (keeping an eye on the alpha inflation problem), etc.
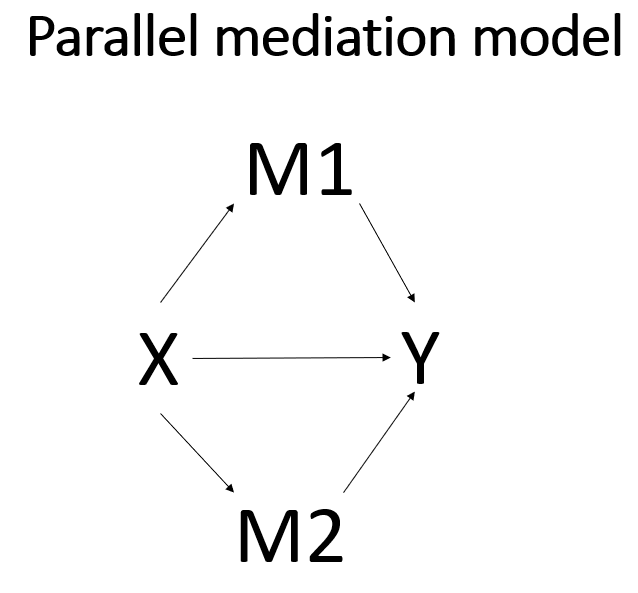
Parallel mediation
In a parallel mediation model, you have two (or more) mediators, both of which are between the predictor and outcome. We will continue to use the variable feeling as one mediator, and we will add the variable impact as the second mediator. In this example, there is no causal path between the two mediators, but one could be added if theory predicted a path to be there. Of course, now you have two sets of indirect effects: the indirect effect going through the first mediator, and the indirect effect going through the second mediator. In PROCESS, you simply add list all of the mediators on the m subcommand and use model 4. Below is a path diagram describing the model. Following that are the series of regression commands that could be run in SPSS to get the path coefficients. A few of the tables from each regression output have been omitted to save space.
regression /dep = feeling /method = enter detail.
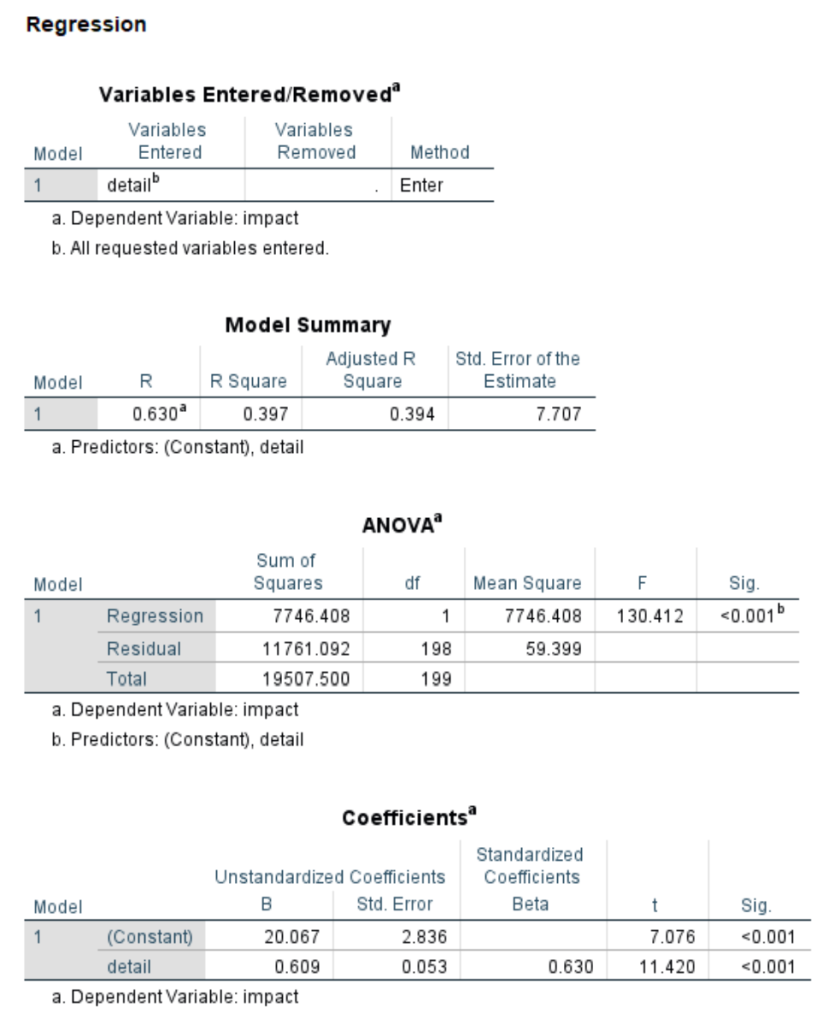
regression /dep = impact /method = enter detail.
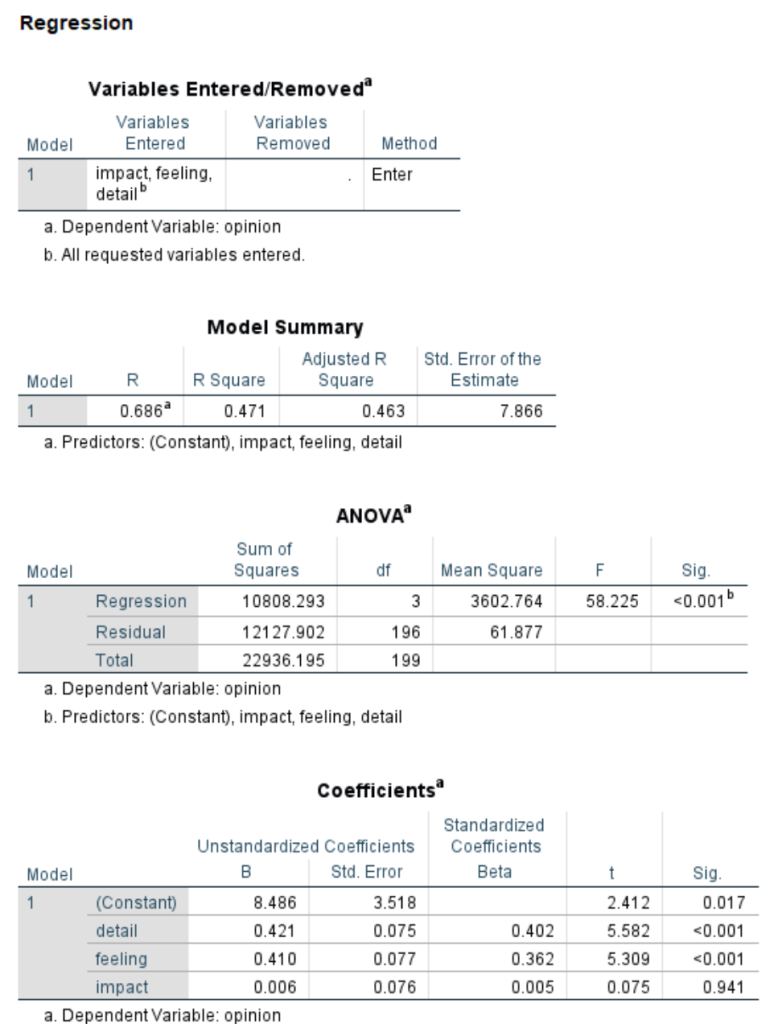
regression /dep = opinion /method = enter detail feeling impact.
The PROCESS command for this model is given below. Notice that we are still using model 4 but have listed more than one mediator on the m subcommand. In a parallel mediation model, the order in which the mediators are listed does not matter. We continue to use the total and seed optional subcommands.
process y = opinion /x = detail /m = feeling impact /total = 1 /model = 4 /seed = 30802022.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 4
Y : opinion
X : detail
M1 : feeling
M2 : impact
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5968 .3561 58.1387 109.5213 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 23.9594 2.8057 8.5394 .0000 18.4265 29.4924
detail .5517 .0527 10.4652 .0000 .4477 .6557
**************************************************************************
OUTCOME VARIABLE:
impact
Model Summary
R R-sq MSE F df1 df2 p
.6302 .3971 59.3995 130.4121 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 20.0670 2.8360 7.0758 .0000 14.4743 25.6596
detail .6085 .0533 11.4198 .0000 .5034 .7136
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6865 .4712 61.8771 58.2246 3.0000 196.0000 .0000
Model
coeff se t p LLCI ULCI
constant 8.4863 3.5180 2.4122 .0168 1.5482 15.4243
detail .4213 .0755 5.5825 .0000 .2724 .5701
feeling .4097 .0772 5.3089 .0000 .2575 .5619
impact .0057 .0763 .0746 .9406 -.1449 .1563
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6215 .3862 71.0973 124.6031 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 18.4162 3.1027 5.9355 .0000 12.2976 24.5348
detail .6508 .0583 11.1626 .0000 .5358 .7657
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se t p LLCI ULCI
.6508 .0583 11.1626 .0000 .5358 .7657
Direct effect of X on Y
Effect se t p LLCI ULCI
.4213 .0755 5.5825 .0000 .2724 .5701
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
TOTAL .2295 .0619 .1076 .3531
feeling .2260 .0491 .1317 .3237
impact .0035 .0503 -.0890 .1070
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
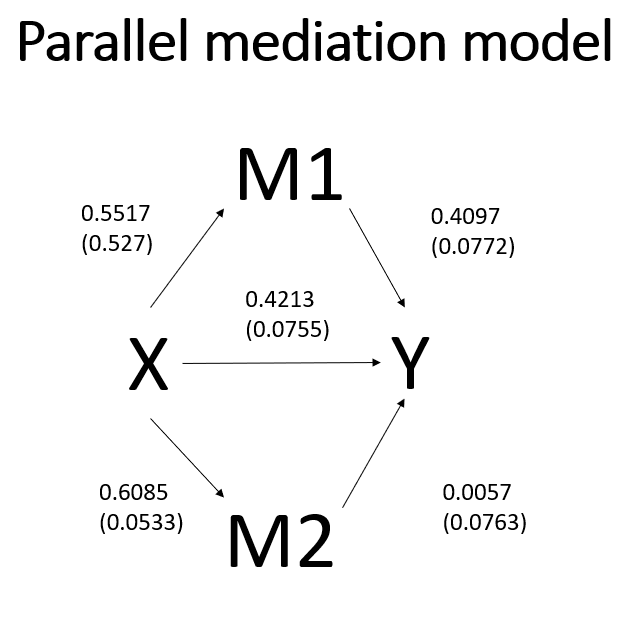
The interpretation of the path coefficients is the same as in previous models, except that now we include “holding both mediators constant” when discussing the direct effect or “holding the other mediator constant” when discussing one of the mediators. Looking at the second to last part of the output above, we see that we are given the total indirect effect, 0.2295, as well as the indirect effect via feeling, 0.2260, and the indirect effect via impact, 0.0035.
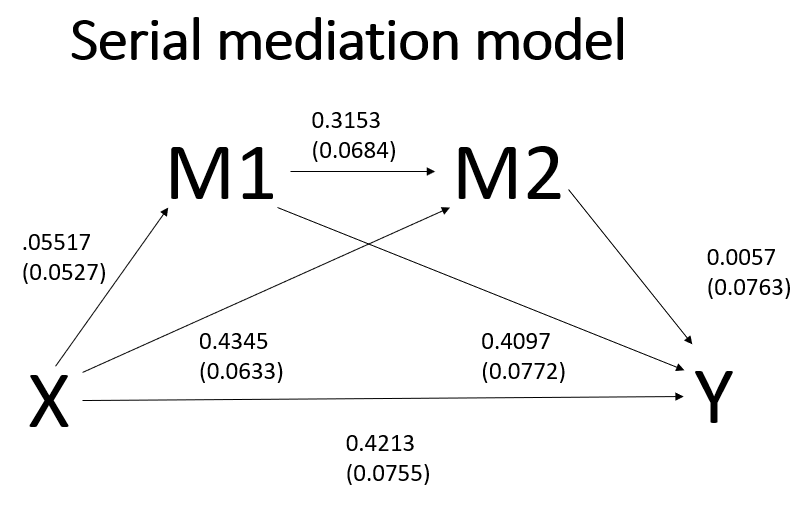
Serial mediation
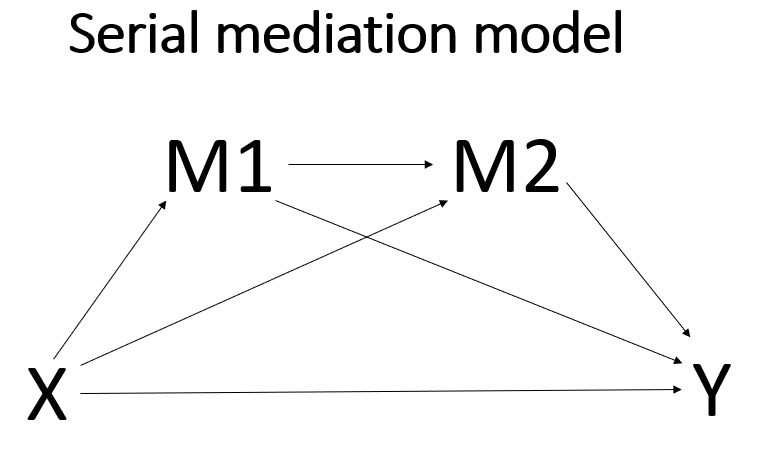
In a serial mediation model, the mediators are ordered between the predictor and the outcome. There may or may not be causal arrows between the mediators; that should be determined by theory. When specifying a serial mediation model, the order in which the mediators are listed on the m subcommand is important! The first mediator that you list is the first mediator in the model, the second mediator that you list is the second one in the model, and so on. PROCESS will allow up to six mediators in a single model, although there are few research situations (and datasets) that would allow for so many mediators.
process y = opinion /x = detail /m = feeling impact /total = 1 /contrast = 1 /model = 6 /seed = 30802022.
Run MATRIX procedure:
***************** PROCESS Procedure for SPSS Version 4.0 *****************
Written by Andrew F. Hayes, Ph.D. www.afhayes.com
Documentation available in Hayes (2022). www.guilford.com/p/hayes3
**************************************************************************
Model : 6
Y : opinion
X : detail
M1 : feeling
M2 : impact
Sample
Size: 200
Custom
Seed: 30802022
**************************************************************************
OUTCOME VARIABLE:
feeling
Model Summary
R R-sq MSE F df1 df2 p
.5968 .3561 58.1387 109.5213 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 23.9594 2.8057 8.5394 .0000 18.4265 29.4924
detail .5517 .0527 10.4652 .0000 .4477 .6557
**************************************************************************
OUTCOME VARIABLE:
impact
Model Summary
R R-sq MSE F df1 df2 p
.6751 .4558 53.8901 82.4933 2.0000 197.0000 .0000
Model
coeff se t p LLCI ULCI
constant 12.5114 3.1598 3.9596 .0001 6.2801 18.7428
detail .4345 .0633 6.8699 .0000 .3098 .5593
feeling .3153 .0684 4.6089 .0000 .1804 .4503
**************************************************************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6865 .4712 61.8771 58.2246 3.0000 196.0000 .0000
Model
coeff se t p LLCI ULCI
constant 8.4863 3.5180 2.4122 .0168 1.5482 15.4243
detail .4213 .0755 5.5825 .0000 .2724 .5701
feeling .4097 .0772 5.3089 .0000 .2575 .5619
impact .0057 .0763 .0746 .9406 -.1449 .1563
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
opinion
Model Summary
R R-sq MSE F df1 df2 p
.6215 .3862 71.0973 124.6031 1.0000 198.0000 .0000
Model
coeff se t p LLCI ULCI
constant 18.4162 3.1027 5.9355 .0000 12.2976 24.5348
detail .6508 .0583 11.1626 .0000 .5358 .7657
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se t p LLCI ULCI
.6508 .0583 11.1626 .0000 .5358 .7657
Direct effect of X on Y
Effect se t p LLCI ULCI
.4213 .0755 5.5825 .0000 .2724 .5701
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
TOTAL .2295 .0619 .1076 .3531
Ind1 .2260 .0491 .1317 .3237
Ind2 .0025 .0361 -.0656 .0760
Ind3 .0010 .0148 -.0255 .0335
(C1) .2235 .0671 .0895 .3532
(C2) .2250 .0544 .1190 .3334
(C3) .0015 .0228 -.0448 .0488
Specific indirect effect contrast definition(s):
(C1) Ind1 minus Ind2
(C2) Ind1 minus Ind3
(C3) Ind2 minus Ind3
Indirect effect key:
Ind1 detail -> feeling -> opinion
Ind2 detail -> impact -> opinion
Ind3 detail -> feeling -> impact -> opinion
*********************** ANALYSIS NOTES AND ERRORS ************************
Level of confidence for all confidence intervals in output:
95.0000
Number of bootstrap samples for percentile bootstrap confidence intervals:
5000
------ END MATRIX -----
Some of the subcommands available in PROCESS
y: outcome variable (must be either continuous or binary)
x: predictor variable (may be continuous, binary or multicategorical)
m: mediator(s) (must be continuous)
w: first moderator
z: second moderator
model: specify the model number (models numbers found in Appendix A of Introduction to Mediation, Moderation and Conditional Process Analysis: A Regression-based Approach, Third Edition by Andrew F. Hayes (2022).)
seed: allows user to set the seed so that analyses will replicate exactly
stand: = 1: gives standardized coefficients (or partially standardized coefficients if X is binary)
conf: allows user to set the confidence interval (default is 95% CIs)
cov: covariates to be included in all models (may be continuous or binary)
boot: allows user to set the number of bootstrapped samples (default is 5000)
modelbt: = 1: requests bootstrapped standard errors and confidence intervals for all model estimates
hc: = 0: HC0: Based on the original asymptotic or large sample robust, empirical, or “sandwich” estimator of the covariance matrix of the parameter estimates. The middle part of the sandwich contains squared OLS (ordinary least squares) or squared weighted WLS (weighted least squares) residuals.
= 1: HC1: A finite-sample modification of HC0, multiplying it by N/(N-p), where N is the sample size and p is the number of non-redundant parameters in the model.
= 2 HC2: A modification of HC0 that involves dividing the squared residual by 1-h, where h is the leverage for the case.
= 3: HC3: A modification of HC0 that approximates a jackknife estimator. Squared residuals are divided by the square of 1-h. This method is the default if ROBUST is specified without specifying a method.
= 4: HC4: A modification of HC0 that divides the squared residuals by 1-h to a power that varies according to h, N, and p, with an upper limit of 4. NOTE: These definitions are quoted from page 852 of the SPSS version 28 Command Syntax Reference.
decimals: controls the number of decimal places shown in the output; use SPSS formats, such as f10.2 for two decimal places; the default is four.
mcx: indicates that the X variable is multicategorical; = 1: indicator (AKA dummy) coding; = 2: sequential coding; = 3: Helmert coding; = 4: effect coding
mcw: indicates that the W variable is multicategorical; = 1: indicator (AKA dummy) coding; = 2: sequential coding; = 3: Helmert coding; = 4: effect coding
mcz: indicates that the Z variable is multicategorical; = 1: indicator (AKA dummy) coding; = 2: sequential coding; = 3: Helmert coding; = 4: effect coding
longname: variable names should be eight characters or less. If the variable names are longer than eight characters, use longname = 1. However, PROCESS still only looks at the first eight characters of the variable name. This will be problematic if two or more variable names have the same first eight characters.
effsize: (replace with stand in version 4 of the macro)
total: adds the total effect to the output.
normal: calculates the standard errors using normal theory (not recommended).
contrast: = 1: a test for the difference between their regression weights; = 2: a test for the difference of the absolute values of their regression weights, may be useful if you want to compare one positive indirect effect to a negative one in order to assess whether the positive one is (in absolute terms) significantly larger than the negative one.
matrices: = 1: shows the bmatrix
bmatrix: (FROM variables are columns, TO variables are rows) (BMATRIX: Paths freely estimated (1) and fixed to zero (0))
wmatrix: (paths moderated and not moderated by W) (FROM variables are columns, TO variables are rows)
zmatrix: (paths moderated and not moderated by Z) (FROM variables are columns, TO variables are rows)
Criteria for making causal claims
The criteria for making causal claims has changed greatly in the last 10-15 years. Gone are the days of Baron and Kenny and the causal steps approach. Hayes provides a thoughtful explanation of why this method, that was so widely used for 20 years, is no longer acceptable. The work of Judea Pearl and Tyler VanderWeele have been very influential in this change. A complete discussion of the current set of criteria needed to claim causality is beyond the scope of this workshop, but a few important points will be made. First, and perhaps most obvious, the predictor must precede the mediator which must precede the outcome in time. In other words, the cause must come before the effect. This means that cross-sectional data are usually inappropriate for mediation analysis, because all of the data (for X, M and Y) are collected at the same time, so there is no way to guarantee that the cause happened before the effect. Second, just because you used a particular variable as the mediator does not mean that it is the only mediator. Perhaps another variable is the real mediator, and the variable you are using is just correlated with the real mediator. Or perhaps a variable that is not in your model, and maybe not even in your dataset, causes both the mediator and the outcome. When thinking about experiments and causality, most researchers immediately think of randomly assigning subjects to experimental groups or conditions; however, such assignment does not mean that mediator causes the outcome.
In his paper Mediation Analysis: A Practitioner’s Guide (2015), VanderWeele lists four assumptions that need to be assessed so that the direct and indirect effects are interpretable.
- no confounding between X and Y
- no confounding between M and Y
- no confounding between X and M
- no confounding between M and Y that is itself affected by X.
As you can see, many of these assumptions are not testable using the dataset at hand, but rather must be made on a logical basis.
With respect to writing up a mediation analysis, please be sure to check on the current guidelines. They have changed quite a bit in the last few years, and they will probably continue to change for some time to come.