Chapter Outline
1.0 Introduction
1.1 A First Regression Analysis
1.2 Examining Data
1.3 Simple linear regression
1.4 Multiple regression
1.5 Transforming variables
1.6 Summary
1.7 For more information
1.0 Introduction
This web book is composed of three chapters covering a variety of topics about using SPSS for regression. We should emphasize that this book is about "data analysis" and that it demonstrates how SPSS can be used for regression analysis, as opposed to a book that covers the statistical basis of multiple regression. We assume that you have had at least one statistics course covering regression analysis and that you have a regression book that you can use as a reference (see the Regression With SPSS page and our Statistics Books for Loan page for recommended regression analysis books). This book is designed to apply your knowledge of regression, combine it with instruction on SPSS, to perform, understand and interpret regression analyses.
This first chapter will cover topics in simple and multiple regression, as well as the supporting tasks that are important in preparing to analyze your data, e.g., data checking, getting familiar with your data file, and examining the distribution of your variables. We will illustrate the basics of simple and multiple regression and demonstrate the importance of inspecting, checking and verifying your data before accepting the results of your analysis. In general, we hope to show that the results of your regression analysis can be misleading without further probing of your data, which could reveal relationships that a casual analysis could overlook.
In this chapter, and in subsequent chapters, we will be using a data file that was created by randomly sampling 400 elementary schools from the California Department of Education’s API 2000 dataset. This data file contains a measure of school academic performance as well as other attributes of the elementary schools, such as, class size, enrollment, poverty, etc.
You can access this data file over the web by clicking on elemapi.sav, or by visiting the Regression with SPSS page where you can download all of the data files used in all of the chapters of this book. The examples will assume you have stored your files in a folder called c:spssreg, but actually you can store the files in any folder you choose, but if you run these examples be sure to change c:spssreg to the name of the folder you have selected.
1.1 A First Regression Analysis
Let’s dive right in and perform a regression analysis using api00 as the outcome variable and the variables acs_k3, meals and full as predictors. These measure the academic performance of the school (api00), the average class size in kindergarten through 3rd grade (acs_k3), the percentage of students receiving free meals (meals) – which is an indicator of poverty, and the percentage of teachers who have full teaching credentials (full). We expect that better academic performance would be associated with lower class size, fewer students receiving free meals, and a higher percentage of teachers having full teaching credentials. Below, we use the regression command for running this regression. The /dependent subcommand indicates the dependent variable, and the variables following /method=enter are the predictors in the model. This is followed by the output of these SPSS commands.
get file = "c:spssregelemapi.sav". regression /dependent api00 /method=enter acs_k3 meals full.
| Model | Variables Entered | Variables Removed | Method |
|---|---|---|---|
| 1 | FULL, ACS_K3, MEALS(a) | . | Enter |
| a All requested variables entered. | |||
| b Dependent Variable: API00 | |||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
|---|---|---|---|---|
| 1 | .821(a) | .674 | .671 | 64.153 |
| a Predictors: (Constant), FULL, ACS_K3, MEALS | ||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|---|
| 1 | Regression | 2634884.261 | 3 | 878294.754 | 213.407 | .000(a) |
| Residual | 1271713.209 | 309 | 4115.577 | |||
| Total | 3906597.470 | 312 | ||||
| a Predictors: (Constant), FULL, ACS_K3, MEALS | ||||||
| b Dependent Variable: API00 | ||||||
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |||
|---|---|---|---|---|---|---|
| Model | B | Std. Error | Beta | |||
| 1 | (Constant) | 906.739 | 28.265 | 32.080 | .000 | |
| ACS_K3 | -2.682 | 1.394 | -.064 | -1.924 | .055 | |
| MEALS | -3.702 | .154 | -.808 | -24.038 | .000 | |
| FULL | .109 | .091 | .041 | 1.197 | .232 | |
| a Dependent Variable: API00 | ||||||
Let's focus on the three predictors, whether they are statistically significant and, if so, the direction of the relationship. The average class size (acs_k3, b=-2.682) is not significant (p=0.055), but only just so, and the coefficient is negative which would indicate that larger class sizes is related to lower academic performance -- which is what we would expect. Next, the effect of meals (b=-3.702, p=.000) is significant and its coefficient is negative indicating that the greater the proportion students receiving free meals, the lower the academic performance. Please note that we are not saying that free meals are causing lower academic performance. The meals variable is highly related to income level and functions more as a proxy for poverty. Thus, higher levels of poverty are associated with lower academic performance. This result also makes sense. Finally, the percentage of teachers with full credentials (full, b=0.109, p=.2321) seems to be unrelated to academic performance. This would seem to indicate that the percentage of teachers with full credentials is not an important factor in predicting academic performance -- this result was somewhat unexpected.
Should we take these results and write them up for publication? From these results, we would conclude that lower class sizes are related to higher performance, that fewer students receiving free meals is associated with higher performance, and that the percentage of teachers with full credentials was not related to academic performance in the schools. Before we write this up for publication, we should do a number of checks to make sure we can firmly stand behind these results. We start by getting more familiar with the data file, doing preliminary data checking, and looking for errors in the data.
1.2 Examining data
To get a better feeling for the contents of this file let's use display names to see the names of the variables in our data file.
display names. Currently Defined Variables SNUM API99 ELL ACS_K3 HSG GRAD_SCH FULL ENROLL DNUM GROWTH YR_RND ACS_46 SOME_COL AVG_ED EMER MEALCAT API00 MEALS MOBILITY NOT_HSG COL_GRAD
Next, we can use display labels to see the names and the labels associated with the variables in our data file. We can see that we have 21 variables and the labels describing each of the variables.
display labels.
List of variables on the working file
Name Position Label
SNUM 1 school number
DNUM 2 district number
API00 3 api 2000
API99 4 api 1999
GROWTH 5 growth 1999 to 2000
MEALS 6 pct free meals
ELL 7 english language learners
YR_RND 8 year round school
MOBILITY 9 pct 1st year in school
ACS_K3 10 avg class size k-3
ACS_46 11 avg class size 4-6
NOT_HSG 12 parent not hsg
HSG 13 parent hsg
SOME_COL 14 parent some college
COL_GRAD 15 parent college grad
GRAD_SCH 16 parent grad school
AVG_ED 17 avg parent ed
FULL 18 pct full credential
EMER 19 pct emer credential
ENROLL 20 number of students
MEALCAT 21 Percentage free meals in 3 categories
We will not go into all of the details about these variables. We have variables about academic performance in 2000 and 1999 and the change in performance, api00, api99 and growth respectively. We also have various characteristics of the schools, e.g., class size, parents education, percent of teachers with full and emergency credentials, and number of students.
Another way you can learn more about the data file is by using list cases to show some of the observations. For example, below we list cases to show the first five observations.
list /cases from 1 to 5.
The variables are listed in the following order:
LINE 1: SNUM DNUM API00 API99 GROWTH MEALS ELL YR_RND MOBILITY ACS_K3 ACS_46
LINE 2: NOT_HSG HSG SOME_COL COL_GRAD GRAD_SCH AVG_ED FULL EMER ENROLL
LINE 3: MEALCAT
SNUM: 906 41 693 600 93 67 9 0 11 16 22
NOT_HSG: 0 0 0 0 0 . 76.00 24 247
MEALCAT: 2
SNUM: 889 41 570 501 69 92 21 0 33 15 32
NOT_HSG: 0 0 0 0 0 . 79.00 19 463
MEALCAT: 3
SNUM: 887 41 546 472 74 97 29 0 36 17 25
NOT_HSG: 0 0 0 0 0 . 68.00 29 395
MEALCAT: 3
SNUM: 876 41 571 487 84 90 27 0 27 20 30
NOT_HSG: 36 45 9 9 0 1.91 87.00 11 418
MEALCAT: 3
SNUM: 888 41 478 425 53 89 30 0 44 18 31
NOT_HSG: 50 50 0 0 0 1.50 87.00 13 520
MEALCAT: 3
Number of cases read: 5 Number of cases listed: 5
This takes up lots of space on the page and is rather hard to read. Listing our data can be very helpful, but it is more helpful if you list just the variables you are interested in. Let's list the first 10 observations for the variables that we looked at in our first regression analysis.
list /variables api00 acs_k3 meals full /cases from 1 to 10.
API00 ACS_K3 MEALS FULL 693 16 67 76.00 570 15 92 79.00 546 17 97 68.00 571 20 90 87.00 478 18 89 87.00 858 20 . 100.00 918 19 . 100.00 831 20 . 96.00 860 20 . 100.00 737 21 29 96.00 Number of cases read: 10 Number of cases listed: 10
We see that among the first 10 observations, we have four missing values for meals. We should keep this in mind.
We can use the descriptives command with /var=all to get descriptive statistics for all of the variables, and pay special attention to the number of valid cases for meals.
descriptives /var=all.
Descriptive Statistics
N
Minimum
Maximum
Mean
Std. Deviation
SNUM
400
58
6072
2866.81
1543.811
DNUM
400
41
796
457.73
184.823
API00
400
369
940
647.62
142.249
API99
400
333
917
610.21
147.136
GROWTH
400
-69
134
37.41
25.247
MEALS
315
6
100
71.99
24.386
ELL
400
0
91
31.45
24.839
YR_RND
400
0
1
.23
.421
MOBILITY
399
2
47
18.25
7.485
ACS_K3
398
-21
25
18.55
5.005
ACS_46
397
20
50
29.69
3.841
NOT_HSG
400
0
100
21.25
20.676
HSG
400
0
100
26.02
16.333
SOME_COL
400
0
67
19.71
11.337
COL_GRAD
400
0
100
19.70
16.471
GRAD_SCH
400
0
67
8.64
12.131
AVG_ED
381
1.00
4.62
2.6685
.76379
FULL
400
.42
100.00
66.0568
40.29793
EMER
400
0
59
12.66
11.746
ENROLL
400
130
1570
483.47
226.448
MEALCAT
400
1
3
2.02
.819
Valid N (listwise)
295
We see that we have 400 observations for most of our variables, but some variables have missing values, like meals which has a valid N of 315. Note that when we did our original regression analysis the DF TOTAL was 312, implying only 313 of the observations were included in the analysis. But, the descriptives command suggests we have 400 observations in our data file.
Let's examine the output more carefully for the variables we used in our regression analysis above, namely api00, acs_k3, meals, full, and yr_rnd. For api00, we see that the values range from 369 to 940 and there are 400 valid values. For acs_k3, the average class size ranges from -21 to 25 and there are 2 missing values. An average class size of -21 sounds wrong, and later we will investigate this further. The variable meals ranges from 6% getting free meals to 100% getting free meals, so these values seem reasonable, but there are only 315 valid values for this variable. The percent of teachers being full credentialed ranges from .42 to 100, and all of the values are valid. The variable yr_rnd ranges from 0 to 1 (which makes sense since this is a dummy variable) and all values are valid.
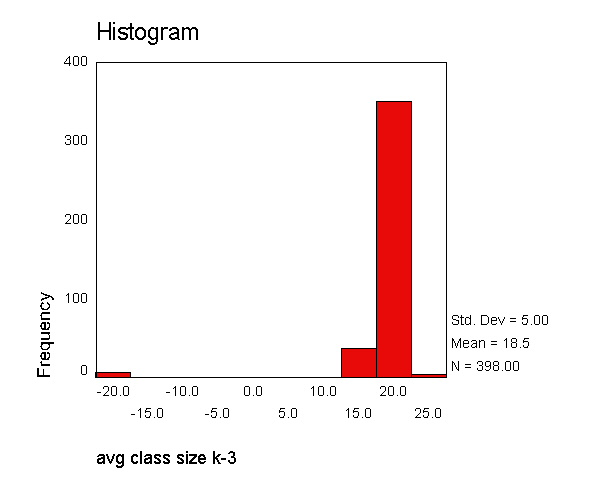
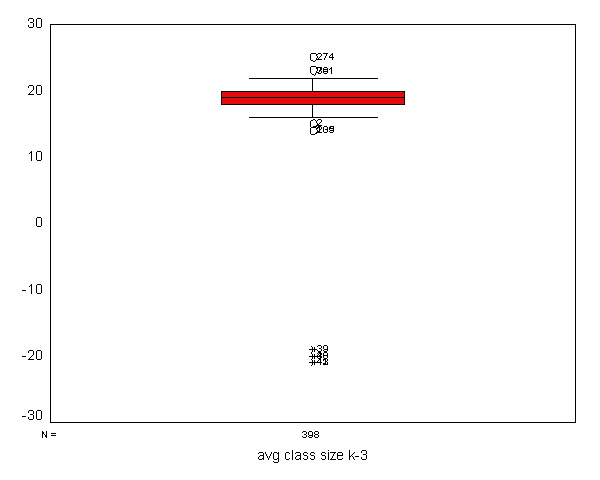
This has uncovered a number of peculiarities worthy of further examination. Let's start with getting more detailed summary statistics for acs_k3 using examine. We will use the histogram stem boxplot options to request a histogram, stem and leaf plot, and a boxplot.
examine /variables=acs_k3 /plot histogram stem boxplot .
| Cases | ||||||
|---|---|---|---|---|---|---|
| Valid | Missing | Total | ||||
| N | Percent | N | Percent | N | Percent | |
| ACS_K3 | 398 | 99.5% | 2 | .5% | 400 | 100.0% |
| Statistic | Std. Error | |||
|---|---|---|---|---|
| ACS_K3 | Mean | 18.55 | .251 | |
| 95% Confidence Interval for Mean | Lower Bound | 18.05 | ||
| Upper Bound | 19.04 | |||
| 5% Trimmed Mean | 19.13 | |||
| Median | 19.00 | |||
| Variance | 25.049 | |||
| Std. Deviation | 5.005 | |||
| Minimum | -21 | |||
| Maximum | 25 | |||
| Range | 46 | |||
| Interquartile Range | 2.00 | |||
| Skewness | -7.106 | .122 | ||
| Kurtosis | 53.014 | .244 | ||
avg class size k-3 Stem-and-Leaf Plot
Frequency Stem & Leaf
9.00 Extremes (=<15.0)
14.00 16 . 00000
.00 16 .
20.00 17 . 0000000
.00 17 .
64.00 18 . 000000000000000000000
.00 18 .
143.00 19 . 000000000000000000000000000000000000000000000000
.00 19 .
97.00 20 . 00000000000000000000000000000000
.00 20 .
40.00 21 . 0000000000000
.00 21 .
7.00 22 . 00
4.00 Extremes (>=23.0)
Stem width: 1
Each leaf: 3 case(s)
We see that the histogram and boxplot are effective in showing the schools with class sizes that are negative. The stem and leaf plot indicates that there are some "Extremes" that are less than 16, but it does not reveal how extreme these values are. Looking at the boxplot and histogram we see observations where the class sizes are around -21 and -20, so it seems as though some of the class sizes somehow became negative, as though a negative sign was incorrectly typed in front of them. Let's do a frequencies for class size to see if this seems plausible.
frequencies /var acs_k3.
| N | Valid | 398 |
|---|---|---|
| Missing | 2 |
| Frequency | Percent | Valid Percent | Cumulative Percent | ||
|---|---|---|---|---|---|
| Valid | -21 | 3 | .8 | .8 | .8 |
| -20 | 2 | .5 | .5 | 1.3 | |
| -19 | 1 | .3 | .3 | 1.5 | |
| 14 | 2 | .5 | .5 | 2.0 | |
| 15 | 1 | .3 | .3 | 2.3 | |
| 16 | 14 | 3.5 | 3.5 | 5.8 | |
| 17 | 20 | 5.0 | 5.0 | 10.8 | |
| 18 | 64 | 16.0 | 16.1 | 26.9 | |
| 19 | 143 | 35.8 | 35.9 | 62.8 | |
| 20 | 97 | 24.3 | 24.4 | 87.2 | |
| 21 | 40 | 10.0 | 10.1 | 97.2 | |
| 22 | 7 | 1.8 | 1.8 | 99.0 | |
| 23 | 3 | .8 | .8 | 99.7 | |
| 25 | 1 | .3 | .3 | 100.0 | |
| Total | 398 | 99.5 | 100.0 | ||
| Missing | System | 2 | .5 | ||
| Total | 400 | 100.0 | |||
Indeed, it seems that some of the class sizes somehow got negative signs put in front of them. Let's look at the school and district number for these observations to see if they come from the same district. Indeed, they all come from district 140.
compute filtvar = (acs_k3 < 0).
filter by filtvar.
list cases
/var snum dnum acs_k3.
filter off.
SNUM DNUM ACS_K3
600 140 -20
596 140 -19
611 140 -20
595 140 -21
592 140 -21
602 140 -21
Now, let's look at all of the observations for district 140.
compute filtvar = (dnum = 140). filter by filtvar. list cases /var snum dnum acs_k3. filter off.
SNUM DNUM ACS_K3
600 140 -20
596 140 -19
611 140 -20
595 140 -21
592 140 -21
602 140 -21
Number of cases read: 6 Number of cases listed: 6
All of the observations from district 140 seem to have this problem. When you find such a problem, you want to go back to the original source of the data to verify the values. We have to reveal that we fabricated this error for illustration purposes, and that the actual data had no such problem. Let's pretend that we checked with district 140 and there was a problem with the data there, a hyphen was accidentally put in front of the class sizes making them negative. We will make a note to fix this! Let's continue checking our data.
We recommend plotting all of these graphs for the variables you will be analyzing. We will omit, due to space considerations, showing these graphs for all of the variables. However, in examining the variables, the histogram for full seemed rather unusual. Up to now, we have not seen anything problematic with this variable, but look at the histogram for full below. It shows over 100 observations where the percent with a full credential that is much lower than all other observations. This is over 25% of the schools, and seems very unusual.
frequencies variables=full /format=notable /histogram .
| N | Valid | 400 |
|---|---|---|
| Missing | 0 |
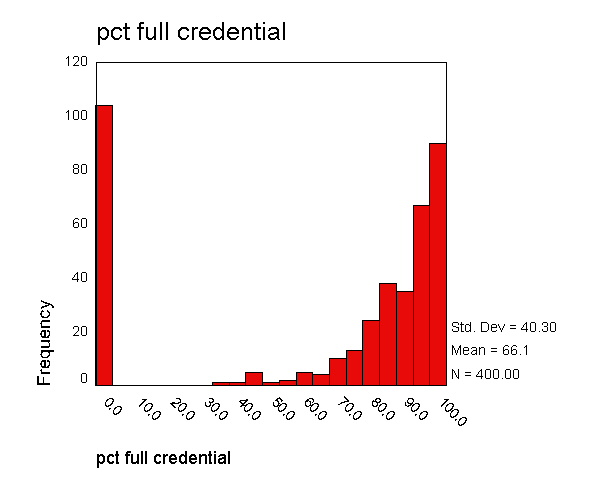
Let's look at the frequency distribution of full to see if we can understand this better. The values go from 0.42 to 1.0, then jump to 37 and go up from there. It appears as though some of the percentages are actually entered as proportions, e.g., 0.42 was entered instead of 42 or 0.96 which really should have been 96.
frequencies variables=full .
| N | Valid | 400 |
|---|---|---|
| Missing | 0 |
| Frequency | Percent | Valid Percent | Cumulative Percent | ||
|---|---|---|---|---|---|
| Valid | .42 | 1 | .3 | .3 | .3 |
| .45 | 1 | .3 | .3 | .5 | |
| .46 | 1 | .3 | .3 | .8 | |
| .47 | 1 | .3 | .3 | 1.0 | |
| .48 | 1 | .3 | .3 | 1.3 | |
| .50 | 3 | .8 | .8 | 2.0 | |
| .51 | 1 | .3 | .3 | 2.3 | |
| .52 | 1 | .3 | .3 | 2.5 | |
| .53 | 1 | .3 | .3 | 2.8 | |
| .54 | 1 | .3 | .3 | 3.0 | |
| .56 | 2 | .5 | .5 | 3.5 | |
| .57 | 2 | .5 | .5 | 4.0 | |
| .58 | 1 | .3 | .3 | 4.3 | |
| .59 | 3 | .8 | .8 | 5.0 | |
| .60 | 1 | .3 | .3 | 5.3 | |
| .61 | 4 | 1.0 | 1.0 | 6.3 | |
| .62 | 2 | .5 | .5 | 6.8 | |
| .63 | 1 | .3 | .3 | 7.0 | |
| .64 | 3 | .8 | .8 | 7.8 | |
| .65 | 3 | .8 | .8 | 8.5 | |
| .66 | 2 | .5 | .5 | 9.0 | |
| .67 | 6 | 1.5 | 1.5 | 10.5 | |
| .68 | 2 | .5 | .5 | 11.0 | |
| .69 | 3 | .8 | .8 | 11.8 | |
| .70 | 1 | .3 | .3 | 12.0 | |
| .71 | 1 | .3 | .3 | 12.3 | |
| .72 | 2 | .5 | .5 | 12.8 | |
| .73 | 6 | 1.5 | 1.5 | 14.3 | |
| .75 | 4 | 1.0 | 1.0 | 15.3 | |
| .76 | 2 | .5 | .5 | 15.8 | |
| .77 | 2 | .5 | .5 | 16.3 | |
| .79 | 3 | .8 | .8 | 17.0 | |
| .80 | 5 | 1.3 | 1.3 | 18.3 | |
| .81 | 8 | 2.0 | 2.0 | 20.3 | |
| .82 | 2 | .5 | .5 | 20.8 | |
| .83 | 2 | .5 | .5 | 21.3 | |
| .84 | 2 | .5 | .5 | 21.8 | |
| .85 | 3 | .8 | .8 | 22.5 | |
| .86 | 2 | .5 | .5 | 23.0 | |
| .90 | 3 | .8 | .8 | 23.8 | |
| .92 | 1 | .3 | .3 | 24.0 | |
| .93 | 1 | .3 | .3 | 24.3 | |
| .94 | 2 | .5 | .5 | 24.8 | |
| .95 | 2 | .5 | .5 | 25.3 | |
| .96 | 1 | .3 | .3 | 25.5 | |
| 1.00 | 2 | .5 | .5 | 26.0 | |
| 37.00 | 1 | .3 | .3 | 26.3 | |
| 41.00 | 1 | .3 | .3 | 26.5 | |
| 44.00 | 2 | .5 | .5 | 27.0 | |
| 45.00 | 2 | .5 | .5 | 27.5 | |
| 46.00 | 1 | .3 | .3 | 27.8 | |
| 48.00 | 1 | .3 | .3 | 28.0 | |
| 53.00 | 1 | .3 | .3 | 28.3 | |
| 57.00 | 1 | .3 | .3 | 28.5 | |
| 58.00 | 3 | .8 | .8 | 29.3 | |
| 59.00 | 1 | .3 | .3 | 29.5 | |
| 61.00 | 1 | .3 | .3 | 29.8 | |
| 63.00 | 2 | .5 | .5 | 30.3 | |
| 64.00 | 1 | .3 | .3 | 30.5 | |
| 65.00 | 1 | .3 | .3 | 30.8 | |
| 68.00 | 2 | .5 | .5 | 31.3 | |
| 69.00 | 3 | .8 | .8 | 32.0 | |
| 70.00 | 1 | .3 | .3 | 32.3 | |
| 71.00 | 3 | .8 | .8 | 33.0 | |
| 72.00 | 1 | .3 | .3 | 33.3 | |
| 73.00 | 2 | .5 | .5 | 33.8 | |
| 74.00 | 1 | .3 | .3 | 34.0 | |
| 75.00 | 4 | 1.0 | 1.0 | 35.0 | |
| 76.00 | 4 | 1.0 | 1.0 | 36.0 | |
| 77.00 | 2 | .5 | .5 | 36.5 | |
| 78.00 | 4 | 1.0 | 1.0 | 37.5 | |
| 79.00 | 3 | .8 | .8 | 38.3 | |
| 80.00 | 10 | 2.5 | 2.5 | 40.8 | |
| 81.00 | 4 | 1.0 | 1.0 | 41.8 | |
| 82.00 | 3 | .8 | .8 | 42.5 | |
| 83.00 | 9 | 2.3 | 2.3 | 44.8 | |
| 84.00 | 4 | 1.0 | 1.0 | 45.8 | |
| 85.00 | 8 | 2.0 | 2.0 | 47.8 | |
| 86.00 | 5 | 1.3 | 1.3 | 49.0 | |
| 87.00 | 12 | 3.0 | 3.0 | 52.0 | |
| 88.00 | 6 | 1.5 | 1.5 | 53.5 | |
| 89.00 | 5 | 1.3 | 1.3 | 54.8 | |
| 90.00 | 9 | 2.3 | 2.3 | 57.0 | |
| 91.00 | 8 | 2.0 | 2.0 | 59.0 | |
| 92.00 | 7 | 1.8 | 1.8 | 60.8 | |
| 93.00 | 12 | 3.0 | 3.0 | 63.8 | |
| 94.00 | 10 | 2.5 | 2.5 | 66.3 | |
| 95.00 | 17 | 4.3 | 4.3 | 70.5 | |
| 96.00 | 17 | 4.3 | 4.3 | 74.8 | |
| 97.00 | 11 | 2.8 | 2.8 | 77.5 | |
| 98.00 | 9 | 2.3 | 2.3 | 79.8 | |
| 100.00 | 81 | 20.3 | 20.3 | 100.0 | |
| Total | 400 | 100.0 | 100.0 | ||
Let's see which district(s) these data came from.
compute filtvar = (full < 1). filter by filtvar. frequencies variables=dnum . filter off.
| N | Valid | 102 |
|---|---|---|
| Missing | 0 |
| Frequency | Percent | Valid Percent | Cumulative Percent | ||
|---|---|---|---|---|---|
| Valid | 401 | 102 | 100.0 | 100.0 | 100.0 |
We note that all 104 observations in which full was less than or equal to one came from district 401. Let's see if this accounts for all of the observations that come from district 401.
compute filtvar = (dnum = 401). filter by filtvar. frequencies variables=dnum . filter off.
| N | Valid | 104 |
|---|---|---|
| Missing | 0 |
| Frequency | Percent | Valid Percent | Cumulative Percent | ||
|---|---|---|---|---|---|
| Valid | 401 | 104 | 100.0 | 100.0 | 100.0 |
All of the observations from this district seem to be recorded as proportions instead of percentages. Again, let us state that this is a pretend problem that we inserted into the data for illustration purposes. If this were a real life problem, we would check with the source of the data and verify the problem. We will make a note to fix this problem in the data as well.
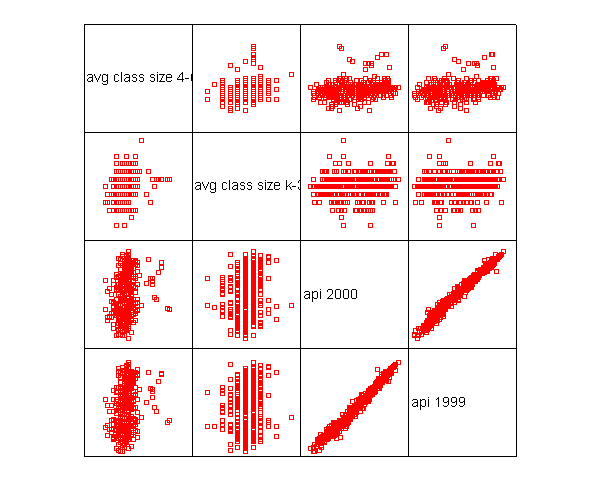
Another useful technique for screening your data is a scatterplot matrix. While this is probably more relevant as a diagnostic tool searching for non-linearities and outliers in your data, but it can also be a useful data screening tool, possibly revealing information in the joint distributions of your variables that would not be apparent from examining univariate distributions. Let's look at the scatterplot matrix for the variables in our regression model. This reveals the problems we have already identified, i.e., the negative class sizes and the percent full credential being entered as proportions.
graph /scatterplot(matrix)=acs_46 acs_k3 api00 api99 .
We have identified three problems in our data. There are numerous missing values for meals, there were negatives accidentally inserted before some of the class sizes (acs_k3) and over a quarter of the values for full were proportions instead of percentages. The corrected version of the data is called elemapi2. Let's use that data file and repeat our analysis and see if the results are the same as our original analysis. But first, let's repeat our original regression analysis below.
regression /dependent api00 /method=enter acs_k3 meals full.<some output omitted to save space>
Coefficients(a) Unstandardized Coefficients Standardized Coefficients t Sig. Model B Std. Error Beta
1 (Constant) 906.739 28.265 32.080 .000 ACS_K3 -2.682 1.394 -.064 -1.924 .055 MEALS -3.702 .154 -.808 -24.038 .000 FULL .109 .091 .041 1.197 .232 a Dependent Variable: API00
Now, let's use the corrected data file and repeat the regression analysis. We see quite a difference in the results! In the original analysis (above), acs_k3 was nearly significant, but in the corrected analysis (below) the results show this variable to be not significant, perhaps due to the cases where class size was given a negative value. Likewise, the percentage of teachers with full credentials was not significant in the original analysis, but is significant in the corrected analysis, perhaps due to the cases where the value was given as the proportion with full credentials instead of the percent. Also, note that the corrected analysis is based on 398 observations instead of 313 observations (which was revealed in the deleted output), due to getting the complete data for the meals variable which had lots of missing values.
get file = "c:spssregelemapi2.sav". regression /dependent api00 /method=enter acs_k3 meals full.
<some output omitted to save space>
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |||
|---|---|---|---|---|---|---|
| Model | B | Std. Error | Beta | |||
| 1 | (Constant) | 771.658 | 48.861 | 15.793 | .000 | |
| ACS_K3 | -.717 | 2.239 | -.007 | -.320 | .749 | |
| MEALS | -3.686 | .112 | -.828 | -32.978 | .000 | |
| FULL | 1.327 | .239 | .139 | 5.556 | .000 | |
| a Dependent Variable: API00 | ||||||
From this point forward, we will use the corrected, elemapi2, data file.
So far we have covered some topics in data checking/verification, but we have not really discussed regression analysis itself. Let's now talk more about performing regression analysis in SPSS.
1.3 Simple Linear Regression
Let's begin by showing some examples of simple linear regression using SPSS. In this type of regression, we have only one predictor variable. This variable may be continuous, meaning that it may assume all values within a range, for example, age or height, or it may be dichotomous, meaning that the variable may assume only one of two values, for example, 0 or 1. The use of categorical variables with more than two levels will be covered in Chapter 3. There is only one response or dependent variable, and it is continuous.
When using SPSS for simple regression, the dependent variable is given in the /dependent subcommand and the predictor is given after the /method=enter subcommand. Let's examine the relationship between the size of school and academic performance to see if the size of the school is related to academic performance. For this example, api00 is the dependent variable and enroll is the predictor.
regression /dependent api00 /method=enter enroll.
| Model | Variables Entered | Variables Removed | Method |
|---|---|---|---|
| 1 | ENROLL(a) | . | Enter |
| a All requested variables entered. | |||
| b Dependent Variable: API00 | |||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
|---|---|---|---|---|
| 1 | .318(a) | .101 | .099 | 135.026 |
| a Predictors: (Constant), ENROLL | ||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|---|
| 1 | Regression | 817326.293 | 1 | 817326.293 | 44.829 | .000(a) |
| Residual | 7256345.704 | 398 | 18232.024 | |||
| Total | 8073671.997 | 399 | ||||
| a Predictors: (Constant), ENROLL | ||||||
| b Dependent Variable: API00 | ||||||
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |||
|---|---|---|---|---|---|---|
| Model | B | Std. Error | Beta | |||
| 1 | (Constant) | 744.251 | 15.933 | 46.711 | .000 | |
| ENROLL | -.200 | .030 | -.318 | -6.695 | .000 | |
| a Dependent Variable: API00 | ||||||
Let's review this output a bit more carefully. First, we see that the F-test is statistically significant, which means that the model is statistically significant. The R-squared is .101 means that approximately 10% of the variance of api00 is accounted for by the model, in this case, enroll. The t-test for enroll equals -6.695 , and is statistically significant, meaning that the regression coefficient for enroll is significantly different from zero. Note that (-6.695)2 = -44.82, which is the same as the F-statistic (with some rounding error). The coefficient for enroll is -.200, meaning that for a one unit increase in enroll, we would expect a .2-unit decrease in api00. In other words, a school with 1100 students would be expected to have an api score 20 units lower than a school with 1000 students. The constant is 744.2514, and this is the predicted value when enroll equals zero. In most cases, the constant is not very interesting. We have prepared an annotated output which shows the output from this regression along with an explanation of each of the items in it.
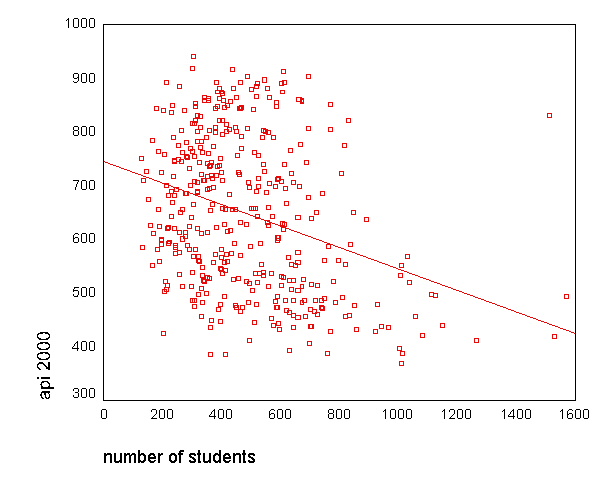
In addition to getting the regression table, it can be useful to see a scatterplot of the predicted and outcome variables with the regression line plotted. You can do this with the graph command as shown below. However, by default, SPSS does not include a regression line and the only way we know to include it is by clicking on the graph and from the pulldown menus choosing Chart then Options and then clicking on the checkbox fit line total to add the regression line. The graph below is what you see after adding the regression line to the graph.
graph /scatterplot(bivar)=enroll with api00 /missing=listwise .
Another kind of graph that you might want to make is a residual versus fitted plot. As shown below, we can use the /scatterplot subcommand as part of the regress command to make this graph. The keywords *zresid and *adjpred in this context refer to the residual value and predicted value from the regression analysis.
regression /dependent api00 /method=enter enroll /scatterplot=(*zresid ,*adjpred ) .<output deleted to save space>
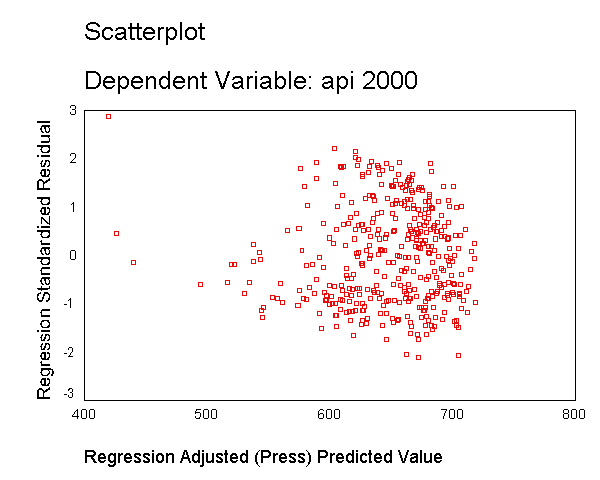
The table below shows a number of other keywords that can be used with the /scatterplot
subcommand and the statistics they display.
| Keyword | Statistic |
|
dependnt |
dependent variable |
| *zpred | standardized predicted values |
| *zresid | standardized residuals |
| *dresid | deleted residuals |
| *adjpred . | adjusted predicted values |
| *sresid | studentized residuals |
| *sdresid | studentized deleted residuals |
1.4 Multiple Regression
Now, let's look at an example of multiple regression, in which we have one outcome (dependent) variable and multiple predictors. For this multiple regression example, we will regress the dependent variable, api00, on all of the predictor variables in the data set.
regression /dependent api00 /method=enter ell meals yr_rnd mobility acs_k3 acs_46 full emer enroll .
| Model | Variables Entered | Variables Removed | Method |
|---|---|---|---|
| 1 | ENROLL, ACS_46, MOBILITY, ACS_K3, EMER, ELL, YR_RND, MEALS, FULL(a) |
. | Enter |
| a All requested variables entered. | |||
| b Dependent Variable: API00 | |||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
|---|---|---|---|---|
| 1 | .919(a) | .845 | .841 | 56.768 |
| a Predictors: (Constant), ENROLL, ACS_46, MOBILITY, ACS_K3, EMER, ELL, YR_RND, MEALS, FULL | ||||
| Model | Sum of Squares |
df | Mean Square |
F | Sig. | |
|---|---|---|---|---|---|---|
| 1 | Regression | 6740702.006 | 9 | 748966.890 | 232.409 | .000(a) |
| Residual | 1240707.781 | 385 | 3222.618 | |||
| Total | 7981409.787 | 394 | ||||
| a Predictors: (Constant), ENROLL, ACS_46, MOBILITY, ACS_K3, EMER, ELL, YR_RND, MEALS, FULL | ||||||
| b Dependent Variable: API00 | ||||||
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |||
|---|---|---|---|---|---|---|
| Model | B | Std. Error | Beta | |||
| 1 | (Constant) | 758.942 | 62.286 | 12.185 | .000 | |
| ELL | -.860 | .211 | -.150 | -4.083 | .000 | |
| MEALS | -2.948 | .170 | -.661 | -17.307 | .000 | |
| YR_RND | -19.889 | 9.258 | -.059 | -2.148 | .032 | |
| MOBILITY | -1.301 | .436 | -.069 | -2.983 | .003 | |
| ACS_K3 | 1.319 | 2.253 | .013 | .585 | .559 | |
| ACS_46 | 2.032 | .798 | .055 | 2.546 | .011 | |
| FULL | .610 | .476 | .064 | 1.281 | .201 | |
| EMER | -.707 | .605 | -.058 | -1.167 | .244 | |
| ENROLL | -1.216E-02 | .017 | -.019 | -.724 | .469 | |
| a Dependent Variable: API00 | ||||||
Let's examine the output from this regression analysis. As with the simple regression, we look to the p-value of the F-test to see if the overall model is significant. With a p-value of zero to three decimal places, the model is statistically significant. The R-squared is 0.845, meaning that approximately 85% of the variability of api00 is accounted for by the variables in the model. In this case, the adjusted R-squared indicates that about 84% of the variability of api00 is accounted for by the model, even after taking into account the number of predictor variables in the model. The coefficients for each of the variables indicates the amount of change one could expect in api00 given a one-unit change in the value of that variable, given that all other variables in the model are held constant. For example, consider the variable ell. We would expect a decrease of 0.86 in the api00 score for every one unit increase in ell, assuming that all other variables in the model are held constant. The interpretation of much of the output from the multiple regression is the same as it was for the simple regression. We have prepared an annotated output that more thoroughly explains the output of this multiple regression analysis.
You may be wondering what a 0.86 change in ell really means, and how you might compare the strength of that coefficient to the coefficient for another variable, say meals. To address this problem, we can refer to the column of Beta coefficients, also known as standardized regression coefficients. The beta coefficients are used by some researchers to compare the relative strength of the various predictors within the model. Because the beta coefficients are all measured in standard deviations, instead of the units of the variables, they can be compared to one another. In other words, the beta coefficients are the coefficients that you would obtain if the outcome and predictor variables were all transformed to standard scores, also called z-scores, before running the regression. In this example, meals has the largest Beta coefficient, -0.661, and acs_k3 has the smallest Beta, 0.013. Thus, a one standard deviation increase in meals leads to a 0.661 standard deviation decrease in predicted api00, with the other variables held constant. And, a one standard deviation increase in acs_k3, in turn, leads to a 0.013 standard deviation increase api00 with the other variables in the model held constant.
In interpreting this output, remember that the difference between the regular coefficients and the standardized coefficients is the units of measurement. For example, to describe the raw coefficient for ell you would say "A one-unit decrease in ell would yield a .86-unit increase in the predicted api00." However, for the standardized coefficient (Beta) you would say, "A one standard deviation decrease in ell would yield a .15 standard deviation increase in the predicted api00."
So far, we have concerned ourselves with testing a single variable at a time, for example looking at the coefficient for ell and determining if that is significant. We can also test sets of variables, using test on the /method subcommand, to see if the set of variables is significant. First, let's start by testing a single variable, ell, using the /method=test subcommand. Note that we have two /method subcommands, the first including all of the variables we want, except for ell, using /method=enter . Then, the second subcommand uses /method=test(ell) to indicate that we wish to test the effect of adding ell to the model previously specified.
As you see in the output below, SPSS forms two models, the first with all of the variables specified in the first /model subcommand that indicates that the 8 variables in the first model are significant (F=249.256). Then, SPSS adds ell to the model and reports an F test evaluating the addition of the variable ell, with an F value of 16.673 and a p value of 0.000, indicating that the addition of ell is significant. Then, SPSS reports the significance of the overall model with all 9 variables, and the F value for that is 232.4 and is significant.
regression /dependent api00 /method=enter meals yr_rnd mobility acs_k3 acs_46 full emer enroll /method=test(ell).
Variables Entered/Removed(b) Model Variables Entered Variables Removed Method 1 ENROLL, ACS_46, MOBILITY, ACS_K3,
EMER, MEALS, YR_RND, FULL(a). Enter 2 ELL . Test a All requested variables entered. b Dependent Variable: API00
Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .915(a) .838 .834 57.909 2 .919(b) .845 .841 56.768 a Predictors: (Constant), ENROLL, ACS_46, MOBILITY, ACS_K3,
EMER, MEALS, YR_RND, FULLb Predictors: (Constant), ENROLL, ACS_46, MOBILITY, ACS_K3,
EMER, MEALS, YR_RND, FULL, ELL
ANOVA(d) Model Sum of
Squaresdf Mean
SquareF Sig. R Square
Change1 Regression 6686970.454 835871.307 249.256 .000(a) Residual 1294439.333 386 3353.470 Total 7981409.787 394 2 Subset Tests ELL 53731.552 1 53731.552 16.673 .000(b) .007 Regression 6740702.006 9 748966.890 232.409 .000(c) Residual 1240707.781 385 3222.618 Total 7981409.787 394 a Predictors: (Constant), ENROLL, ACS_46, MOBILITY, ACS_K3,
EMER, MEALS, YR_RND, FULLb Tested against the full model. c Predictors in the Full Model: (Constant), ENROLL, ACS_46, MOBILITY,
ACS_K3, EMER, MEALS, YR_RND, FULL, ELL.d Dependent Variable: API00
Coefficients(a) Unstandardized Coefficients Standardized Coefficients t Sig. Model B Std. Error Beta
1 (Constant) 779.331 63.333 12.305 .000 MEALS -3.447 .121 -.772 -28.427 .000 YR_RND -24.029 9.388 -.071 -2.560 .011 MOBILITY -.728 .421 -.038 -1.728 .085 ACS_K3 .178 2.280 .002 .078 .938 ACS_46 2.097 .814 .057 2.575 .010 FULL .632 .485 .066 1.301 .194 EMER -.670 .618 -.055 -1.085 .279 ENROLL -3.092E-02 .016 -.049 -1.876 .061 2 (Constant) 758.942 62.286 12.185 .000 MEALS -2.948 .170 -.661 -17.307 .000 YR_RND -19.889 9.258 -.059 -2.148 .032 MOBILITY -1.301 .436 -.069 -2.983 .003 ACS_K3 1.319 2.253 .013 .585 .559 ACS_46 2.032 .798 .055 2.546 .011 FULL .610 .476 .064 1.281 .201 EMER -.707 .605 -.058 -1.167 .244 ENROLL -1.216E-02 .017 -.019 -.724 .469 ELL -.860 .211 -.150 -4.083 .000 a Dependent Variable: API00
Excluded Variables(b) Beta In t Sig. Partial Correlation Collinearity
StatisticsModel
Tolerance1 ELL -.150(a) -4.083 .000 -.204 .301 a Predictors in the Model: (Constant), ENROLL, ACS_46, MOBILITY,
ACS_K3, EMER, MEALS, YR_RND, FULLb Dependent Variable: API00
Perhaps a more interesting test would be to see if the contribution of class size is significant. Since the information regarding class size is contained in two variables, acs_k3 and acs_46, so we include both of these separated in the parentheses of the method-test( ) command. The output below shows the F value for this test is 3.954 with a p value of 0.020, indicating that the overall contribution of these two variables is significant. One way to think of this, is that there is a significant difference between a model with acs_k3 and acs_46 as compared to a model without them, i.e., there is a significant difference between the "full" model and the "reduced" models.
regression /dependent api00 /method=enter ell meals yr_rnd mobility full emer enroll /method=test(acs_k3 acs_46).
| Model | Variables Entered | Variables Removed | Method |
|---|---|---|---|
| 1 | ENROLL, MOBILITY, MEALS, EMER, YR_RND, ELL, FULL(a) |
. | Enter |
| 2 | ACS_46, ACS_K3 | . | Test |
| a All requested variables entered. | |||
| b Dependent Variable: API00 | |||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
|---|---|---|---|---|
| 1 | .917(a) | .841 | .838 | 57.200 |
| 2 | .919(b) | .845 | .841 | 56.768 |
| a Predictors: (Constant), ENROLL, MOBILITY, MEALS, EMER, YR_RND, ELL, FULL | ||||
| b Predictors: (Constant), ENROLL, MOBILITY, MEALS, EMER, YR_RND, ELL, FULL, ACS_46, ACS_K3 | ||||
| Model | Sum of Squares |
df | Mean Square |
F | Sig. | R Square Change |
||
|---|---|---|---|---|---|---|---|---|
| 1 | Regression | 6715217.454 | 7 | 959316.779 | 293.206 | .000(a) | ||
| Residual | 1266192.333 | 387 | 3271.815 | |||||
| Total | 7981409.787 | 394 | ||||||
| 2 | Subset Tests |
ACS_K3, ACS_46 |
25484.552 | 2 | 12742.276 | 3.954 | .020(b) | .003 |
| Regression | 6740702.006 | 9 | 748966.890 | 232.409 | .000(c) | |||
| Residual | 1240707.781 | 385 | 3222.618 | |||||
| Total | 7981409.787 | 394 | ||||||
| a Predictors: (Constant), ENROLL, MOBILITY, MEALS, EMER, YR_RND, ELL, FULL | ||||||||
| b Tested against the full model. | ||||||||
| c Predictors in the Full Model: (Constant), ENROLL, MOBILITY, MEALS, EMER, YR_RND, ELL, FULL, ACS_46, ACS_K3. | ||||||||
| d Dependent Variable: API00 | ||||||||
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |||
|---|---|---|---|---|---|---|
| Model | B | Std. Error | Beta | |||
| 1 | (Constant) | 846.223 | 48.053 | 17.610 | .000 | |
| ELL | -.840 | .211 | -.146 | -3.988 | .000 | |
| MEALS | -3.040 | .167 | -.681 | -18.207 | .000 | |
| YR_RND | -18.818 | 9.321 | -.056 | -2.019 | .044 | |
| MOBILITY | -1.075 | .432 | -.057 | -2.489 | .013 | |
| FULL | .589 | .474 | .062 | 1.242 | .215 | |
| EMER | -.763 | .606 | -.063 | -1.258 | .209 | |
| ENROLL | -9.527E-03 | .017 | -.015 | -.566 | .572 | |
| 2 | (Constant) | 758.942 | 62.286 | 12.185 | .000 | |
| ELL | -.860 | .211 | -.150 | -4.083 | .000 | |
| MEALS | -2.948 | .170 | -.661 | -17.307 | .000 | |
| YR_RND | -19.889 | 9.258 | -.059 | -2.148 | .032 | |
| MOBILITY | -1.301 | .436 | -.069 | -2.983 | .003 | |
| FULL | .610 | .476 | .064 | 1.281 | .201 | |
| EMER | -.707 | .605 | -.058 | -1.167 | .244 | |
| ENROLL | -1.216E-02 | .017 | -.019 | -.724 | .469 | |
| ACS_K3 | 1.319 | 2.253 | .013 | .585 | .559 | |
| ACS_46 | 2.032 | .798 | .055 | 2.546 | .011 | |
| a Dependent Variable: API00 | ||||||
| Beta In | t | Sig. | Partial Correlation | Collinearity Statistics | ||
|---|---|---|---|---|---|---|
| Model | Tolerance||||||
| 1 | ACS_K3 | .025(a) | 1.186 | .236 | .060 | .900 |
| ACS_46 | .058(a) | 2.753 | .006 | .139 | .913 | |
| a Predictors in the Model: (Constant), ENROLL, MOBILITY, MEALS, EMER, YR_RND, ELL, FULL | ||||||
| b Dependent Variable: API00 | ||||||
Finally, as part of doing a multiple regression analysis you might be interested in seeing the correlations among the variables in the regression model. You can do this with the correlations command as shown below.
correlations /variables=api00 ell meals yr_rnd mobility acs_k3 acs_46 full emer enroll.
| API00 | ELL | MEALS | YR_ RND |
MOB ILITY |
ACS _K3 |
ACS _46 |
FULL | EMER | ENR OLL |
||
|---|---|---|---|---|---|---|---|---|---|---|---|
| API00 | Pearson Correlation |
1 | -.768 | -.901 | -.475 | -.206 | .171 | .233 | .574 | -.583 | -.318 |
| Sig. (2-tailed) |
. | .000 | .000 | .000 | .000 | .001 | .000 | .000 | .000 | .000 | |
| N | 400 | 400 | 400 | 400 | 399 | 398 | 397 | 400 | 400 | 400 | |
| ELL | Pearson Correlation |
-.768 | 1 | .772 | .498 | -.020 | -.056 | -.173 | -.485 | .472 | .403 |
| Sig. (2-tailed) |
.000 | . | .000 | .000 | .684 | .268 | .001 | .000 | .000 | .000 | |
| N | 400 | 400 | 400 | 400 | 399 | 398 | 397 | 400 | 400 | 400 | |
| MEALS | Pearson Correlation |
-.901 | .772 | 1 | .418 | .217 | -.188 | -.213 | -.528 | .533 | .241 |
| Sig. (2-tailed) |
.000 | .000 | . | .000 | .000 | .000 | .000 | .000 | .000 | .000 | |
| N | 400 | 400 | 400 | 400 | 399 | 398 | 397 | 400 | 400 | 400 | |
| YR_RND | Pearson Correlation |
-.475 | .498 | .418 | 1 | .035 | .023 | -.042 | -.398 | .435 | .592 |
| Sig. (2-tailed) |
.000 | .000 | .000 | . | .488 | .652 | .403 | .000 | .000 | .000 | |
| N | 400 | 400 | 400 | 400 | 399 | 398 | 397 | 400 | 400 | 400 | |
| MOBILITY | Pearson Correlation |
-.206 | -.020 | .217 | .035 | 1 | .040 | .128 | .025 | .060 | .105 |
| Sig. (2-tailed) |
.000 | .684 | .000 | .488 | . | .425 | .011 | .616 | .235 | .036 | |
| N | 399 | 399 | 399 | 399 | 399 | 398 | 396 | 399 | 399 | 399 | |
| ACS_K3 | Pearson Correlation |
.171 | -.056 | -.188 | .023 | .040 | 1 | .271 | .161 | -.110 | .109 |
| Sig. (2-tailed) |
.001 | .268 | .000 | .652 | .425 | . | .000 | .001 | .028 | .030 | |
| N | 398 | 398 | 398 | 398 | 398 | 398 | 395 | 398 | 398 | 398 | |
| ACS_46 | Pearson Correlation |
.233 | -.173 | -.213 | -.042 | .128 | .271 | 1 | .118 | -.124 | .028 |
| Sig. (2-tailed) |
.000 | .001 | .000 | .403 | .011 | .000 | . | .019 | .013 | .574 | |
| N | 397 | 397 | 397 | 397 | 396 | 395 | 397 | 397 | 397 | 397 | |
| FULL | Pearson Correlation |
.574 | -.485 | -.528 | -.398 | .025 | .161 | .118 | 1 | -.906 | -.338 |
| Sig. (2-tailed) |
.000 | .000 | .000 | .000 | .616 | .001 | .019 | . | .000 | .000 | |
| N | 400 | 400 | 400 | 400 | 399 | 398 | 397 | 400 | 400 | 400 | |
| EMER | Pearson Correlation |
-.583 | .472 | .533 | .435 | .060 | -.110 | -.124 | -.906 | 1 | .343 |
| Sig. (2-tailed) |
.000 | .000 | .000 | .000 | .235 | .028 | .013 | .000 | . | .000 | |
| N | 400 | 400 | 400 | 400 | 399 | 398 | 397 | 400 | 400 | 400 | |
| ENROLL | Pearson Correlation |
-.318 | .403 | .241 | .592 | .105 | .109 | .028 | -.338 | .343 | 1 |
| Sig. (2-tailed) |
.000 | .000 | .000 | .000 | .036 | .030 | .574 | .000 | .000 | . | |
| N | 400 | 400 | 400 | 400 | 399 | 398 | 397 | 400 | 400 | 400 | |
We can see that the strongest correlation with api00 is meals with a correlation in excess of -.9. The variables ell and emer are also strongly correlated with api00. All three of these correlations are negative, meaning that as the value of one variable goes down, the value of the other variable tends to go up. Knowing that these variables are strongly associated with api00, we might predict that they would be statistically significant predictor variables in the regression model. Note that the number of cases used for each correlation is determined on a "pairwise" basis, for example there are 398 valid pairs of data for enroll and acs_k3, so that correlation of .1089 is based on 398 observations.
1.5 Transforming Variables
Earlier we focused on screening your data for potential errors. In the next chapter, we will focus on regression diagnostics to verify whether your data meet the assumptions of linear regression. In this section we will focus on the issue of normality. Some researchers believe that linear regression requires that the outcome (dependent) and predictor variables be normally distributed. We need to clarify this issue. In actuality, it is the residuals that need to be normally distributed. In fact, the residuals need to be normal only for the t-tests to be valid. The estimation of the regression coefficients do not require normally distributed residuals. As we are interested in having valid t-tests, we will investigate issues concerning normality.
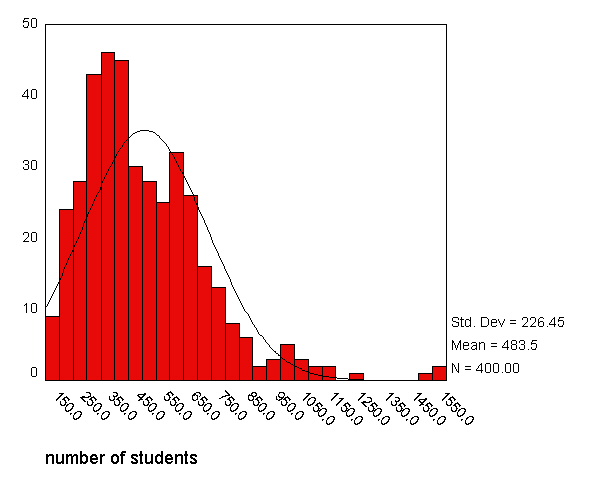
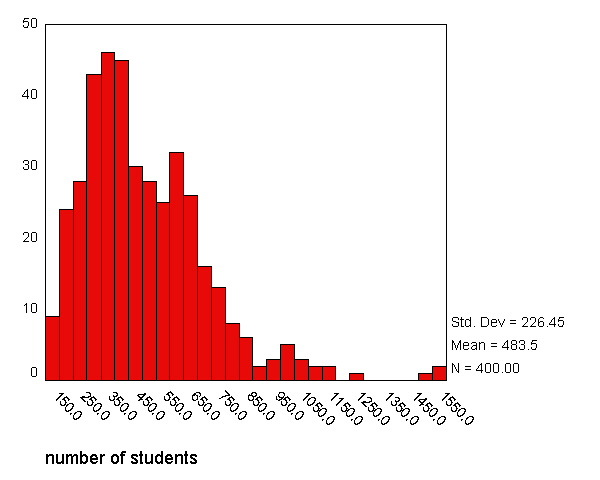
A common cause of non-normally distributed residuals is non-normally distributed outcome and/or predictor variables. So, let us explore the distribution of our variables and how we might transform them to a more normal shape. Let's start by making a histogram of the variable enroll, which we looked at earlier in the simple regression.
graph /histogram=enroll .
We can use the normal option to superimpose a normal curve on this graph. We can see quite a discrepancy between the actual data and the superimposed norml
graph /histogram(normal)=enroll .
We can use the examine command to get a boxplot, stem and leaf plot, histogram, and normal probability plots (with tests of normality) as shown below. There are a number of things indicating this variable is not normal. The skewness indicates it is positively skewed (since it is greater than 0), both of the tests of normality are significant (suggesting enroll is not normal). Also, if enroll was normal, the red boxes on the Q-Q plot would fall along the green line, but instead they deviate quite a bit from the green line.
examine variables=enroll /plot boxplot stemleaf histogram npplot.
| Cases | ||||||
|---|---|---|---|---|---|---|
| Valid | Missing | Total | ||||
| N | Percent | N | Percent | N | Percent | |
| ENROLL | 400 | 100.0% | 0 | .0% | 400 | 100.0% |
| Statistic | Std. Error | |||
|---|---|---|---|---|
| ENROLL | Mean | 483.47 | 11.322 | |
| 95% Confidence Interval for Mean | Lower Bound | 461.21 | ||
| Upper Bound | 505.72 | |||
| 5% Trimmed Mean | 465.70 | |||
| Median | 435.00 | |||
| Variance | 51278.871 | |||
| Std. Deviation | 226.448 | |||
| Minimum | 130 | |||
| Maximum | 1570 | |||
| Range | 1440 | |||
| Interquartile Range | 290.00 | |||
| Skewness | 1.349 | .122 | ||
| Kurtosis | 3.108 | .243 | ||
| Kolmogorov-Smirnov(a) | Shapiro-Wilk | |||||
|---|---|---|---|---|---|---|
| Statistic | df | Sig. | Statistic | df | Sig. | |
| ENROLL | .097 | 400 | .000 | .914 | 400 | .000 |
| a Lilliefors Significance Correction | ||||||
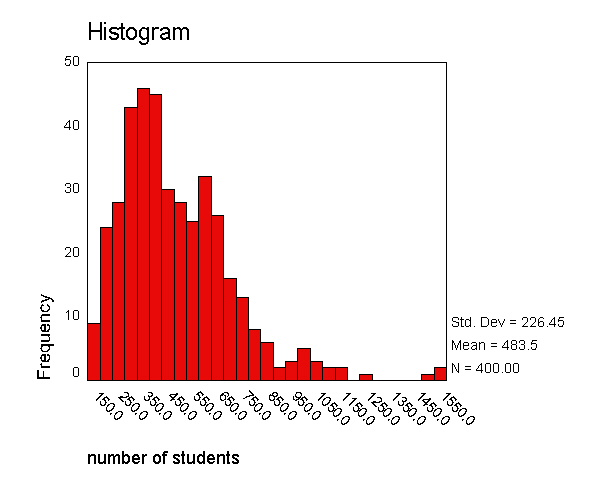
number of students Stem-and-Leaf PlotFrequency Stem & Leaf
4.00 1 . 3& 15.00 1 . 5678899 29.00 2 . 0011122333444 29.00 2 . 5556667788999 47.00 3 . 00000011111222223333344 46.00 3 . 5555566666777888899999 38.00 4 . 000000111111233344 27.00 4 . 5556666688999& 31.00 5 . 00111122223444 28.00 5 . 5556778889999 29.00 6 . 00011112233344 21.00 6 . 555677899 15.00 7 . 001234 9.00 7 . 667& 9.00 8 . 13& 3.00 8 . 5& 3.00 9 . 2& 1.00 9 . & 7.00 10 . 00& 9.00 Extremes (>=1059)
Stem width: 100 Each leaf: 2 case(s)
& denotes fractional leaves.
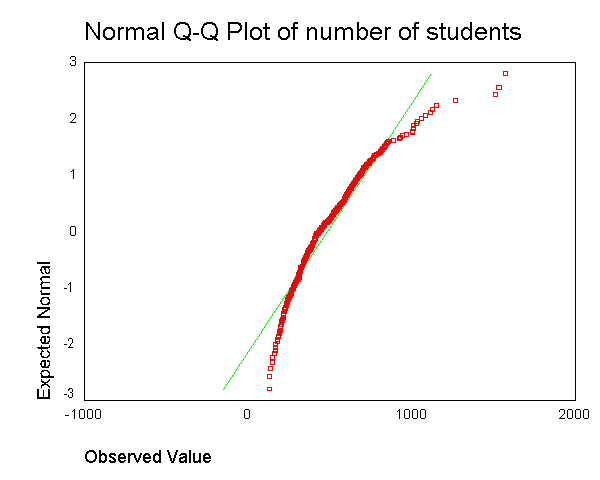
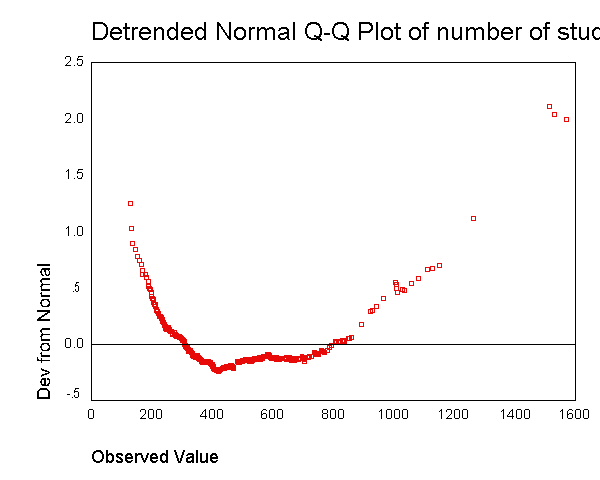
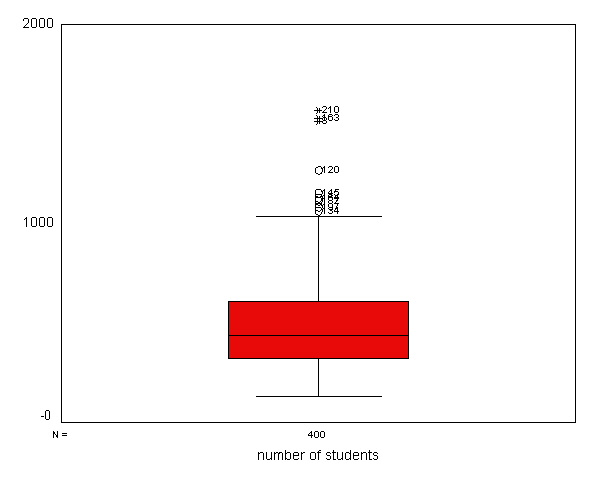
Given the skewness to the right in enroll, let us try a log transformation to see if that makes it more normal. Below we create a variable lenroll that is the natural log of enroll and then we repeat the examine command.
compute lenroll = ln(enroll). examine variables=lenroll /plot boxplot stemleaf histogram npplot.
Case Processing Summary Cases Valid Missing Total N Percent N Percent N Percent LENROLL 400 100.0% 0 .0% 400 100.0%
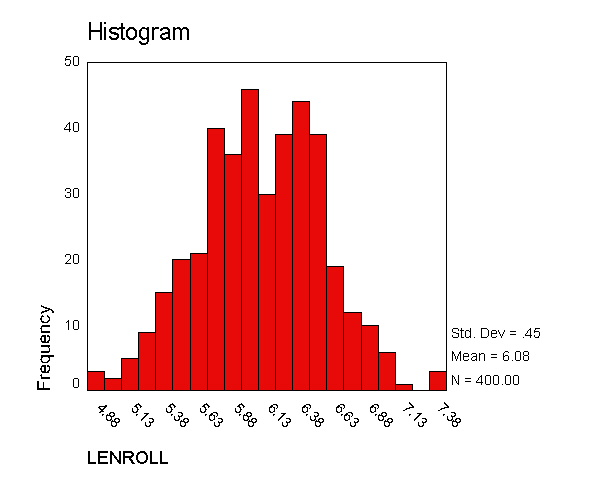
Descriptives Statistic Std. Error LENROLL Mean 6.0792 .02272 95% Confidence Interval for Mean Lower Bound 6.0345 Upper Bound 6.1238 5% Trimmed Mean 6.0798 Median 6.0753 Variance .207 Std. Deviation .45445 Minimum 4.87 Maximum 7.36 Range 2.49 Interquartile Range .6451 Skewness -.059 .122 Kurtosis -.174 .243
Tests of Normality Kolmogorov-Smirnov(a) Shapiro-Wilk Statistic df Sig. Statistic df Sig. LENROLL .038 400 .185 .996 400 .485 a Lilliefors Significance Correction
LENROLL Stem-and-Leaf PlotFrequency Stem & Leaf
4.00 4 . 89 6.00 5 . 011 19.00 5 . 222233333 32.00 5 . 444444445555555 48.00 5 . 666666667777777777777777 67.00 5 . 888888888888888899999999999999999 55.00 6 . 000000000000001111111111111 63.00 6 . 2222222222222222333333333333333 60.00 6 . 44444444444444444455555555555 26.00 6 . 6666666677777 13.00 6 . 889999 4.00 7 . 0& 3.00 7 . 3
Stem width: 1.00 Each leaf: 2 case(s)
& denotes fractional leaves.
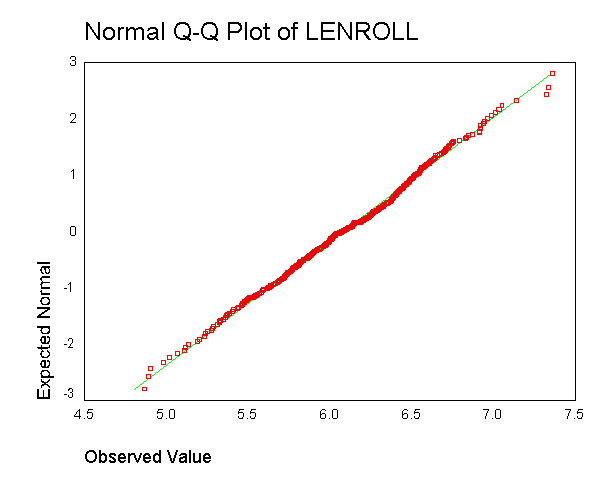
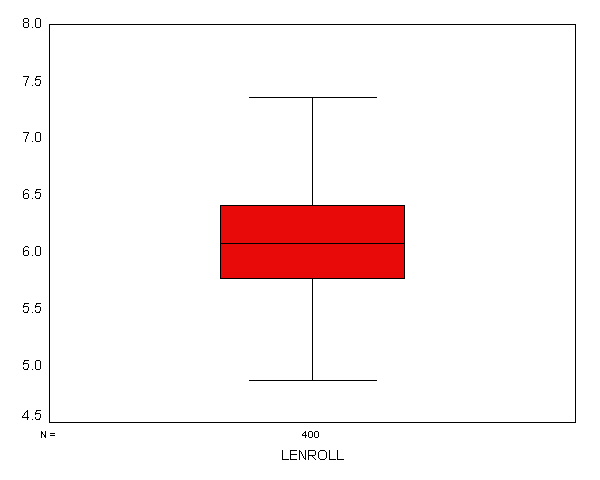
The indications are that lenroll is much more normally distributed --
its skewness and kurtosis are near 0 (which would be normal), the tests of
normality are non-significant, the histogram looks normal, and the red boxes
on the Q-Q plot fall mostly along the green line. Taking the natural log
of enrollment seems to have successfully produced a normally distributed
variable. However, let us emphasize again that the important
consideration is not that enroll (or lenroll) is normally
distributed, but that the residuals from a regression using this variable
would be normally distributed. We will investigate these issues more
fully in chapter 2.
1.6 Summary
In this lecture we have discussed the basics of how to perform simple and multiple regressions, the basics of interpreting output, as well as some related commands. We examined some tools and techniques for screening for bad data and the consequences such data can have on your results. Finally, we touched on the assumptions of linear regression and illustrated how you can check the normality of your variables and how you can transform your variables to achieve normality. The next chapter will pick up where this chapter has left off, going into a more thorough discussion of the assumptions of linear regression and how you can use SPSS to assess these assumptions for your data. In particular, the next lecture will address the following issues.
- Checking for points that exert undue influence on the coefficients
- Checking for constant error variance (homoscedasticity)
- Checking for linear relationships
- Checking model specification
- Checking for multicollinearity
- Checking normality of residuals
1.7 For more information
See the following related web pages for more information.
- SPSS FAQ- How can I do a scatterplot with regression line
- SPSS FAQ- How do I test a group of variables in SPSS ...
- SPSS Textbook Examples- Applied Regression Analysis, Chapter 2
- SPSS Textbook Examples- Applied Regression Analysis, Chapter 3
- SPSS Textbook Examples- Applied Regression Analysis, Chapter 4
- SPSS Textbook Examples- Applied Regression Analysis, Chapter 5
- SPSS Textbook Examples- Applied Regression Analysis, Chapter 6
- SPSS Textbook Examples- Regression with Graphics, Chapter 3