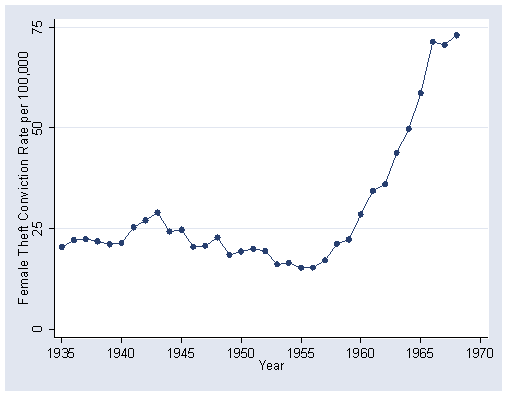
Figure 14.3 on page 380 using data file hartnagl. We use the in option with the use command to omit the first five observations with missing values.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/hartnagl in 5/l, clear (From Fox, Applied Regression Analysis. Use 'notes' command for source of data) graph twoway scatter ftheft year, connect(l) ylabel(0(25)75) xlabel(1935(5)1970)
OLS column of table 14.1 on page 380.
regress ftheft fertil labor postsec mtheft Source | SS df MS Number of obs = 34 ---------+------------------------------ F( 4, 29) = 146.98 Model | 8545.52157 4 2136.38039 Prob > F = 0.0000 Residual | 421.508959 29 14.5347917 R-squared = 0.9530 ---------+------------------------------ Adj R-squared = 0.9465 Total | 8967.03053 33 271.728198 Root MSE = 3.8125 ------------------------------------------------------------------------------ ftheft | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- fertil | -.0060904 .0014495 -4.202 0.000 -.0090549 -.0031258 labor | .1199416 .0234097 5.124 0.000 .0720633 .1678198 postsec | .5515575 .0432509 12.753 0.000 .4630995 .6400156 mtheft | .0393248 .0185559 2.119 0.043 .0013738 .0772758 _cons | -7.334148 9.437921 -0.777 0.443 -26.63686 11.96857 ------------------------------------------------------------------------------
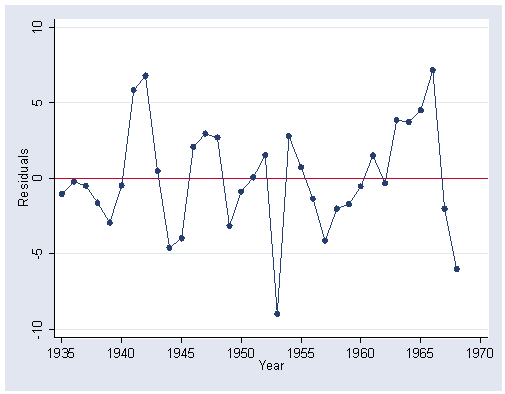
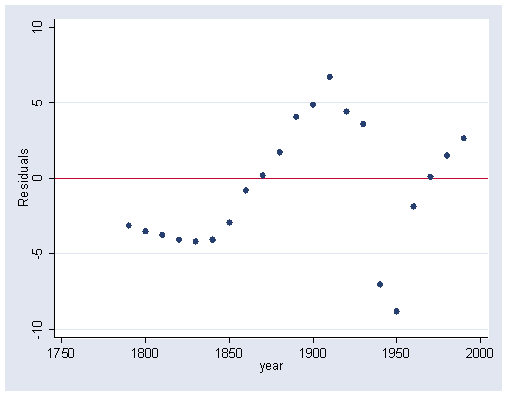
Figure 14.4 on page 381 on residuals from the above OLS regression.
predict r, res graph twoway scatter r year, connect(l) yline(0) ylabel(-10(5)10) xlabel(1935(5)1970)
Continuing table 14.1, page 380: EGLS(1).
tsset year
time variable: year, 1935 to 1968
corrgram r, lags(1) /*get lag-one autocorrelation of the residuals*/
-1 0 1 -1 0 1
LAG AC PAC Q Prob>Q [Autocorrelation] [Partial Autocor]
-------------------------------------------------------------------------------
1 0.2442 0.2673 2.2118 0.1370 |- |--
gen fth1=ftheft-0.244*ftheft[_n-1] /*using transformation on page 378*/
gen fer1=fertil-0.244*fertil[_n-1]
gen lab1 =labor-0.244*labor[_n-1]
gen pos1 = postsec-0.244*postsec[_n-1]
gen mth1 =mtheft-0.244*mtheft[_n-1]
(1 missing value generated in each of the above command.)
gen cons = .756
replace fth1 = sqrt(1-.244*.244)*ftheft if(_n ==1)
replace fer1 = sqrt(1-.244*.244)*fertil if (_n==1)
replace lab1 = sqrt(1-.244*.244)*labor if(_n==1)
replace pos1 = sqrt(1-.244*.244)*postsec if(_n==1)
replace mth1 = sqrt(1-.244*.244)*mtheft if(_n==1)
replace cons = sqrt(1-.244*.244) if(_n==1)
(1 real change made in each of the above command.)
regress fth1 cons fer1 lab1 pos1 mth1, noco
Source | SS df MS Number of obs = 34
---------+------------------------------ F( 5, 29) = 333.75
Model | 22417.159 5 4483.43181 Prob > F = 0.0000
Residual | 389.566176 29 13.4333164 R-squared = 0.9829
---------+------------------------------ Adj R-squared = 0.9800
Total | 22806.7252 34 670.786035 Root MSE = 3.6651
------------------------------------------------------------------------------
fth1 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
cons | -6.64294 11.12007 -0.597 0.555 -29.38604 16.10016
fer1 | -.0058795 .001779 -3.305 0.003 -.0095179 -.002241
lab1 | .1156293 .0270923 4.268 0.000 .0602194 .1710393
pos1 | .5358824 .0500467 10.708 0.000 .4335254 .6382394
mth1 | .0399334 .0219769 1.817 0.080 -.0050144 .0848812
------------------------------------------------------------------------------
Continuing on Table 14.1, page 380: EGLS(2).
regress fth1 cons fer1 lab1 pos1 mth1 in 2/l, noco
Source | SS df MS Number of obs = 33
---------+------------------------------ F( 5, 28) = 318.04
Model | 22027.4862 5 4405.49724 Prob > F = 0.0000
Residual | 387.855476 28 13.8519813 R-squared = 0.9827
---------+------------------------------ Adj R-squared = 0.9796
Total | 22415.3417 33 679.252779 Root MSE = 3.7218
------------------------------------------------------------------------------
fth1 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
cons | -5.518543 11.73656 -0.470 0.642 -29.5598 18.52272
fer1 | -.0060796 .0018941 -3.210 0.003 -.0099596 -.0021996
lab1 | .1136506 .0280815 4.047 0.000 .0561283 .171173
pos1 | .5342096 .051043 10.466 0.000 .4296526 .6387665
mth1 | .0407056 .0224247 1.815 0.080 -.0052293 .0866404
------------------------------------------------------------------------------
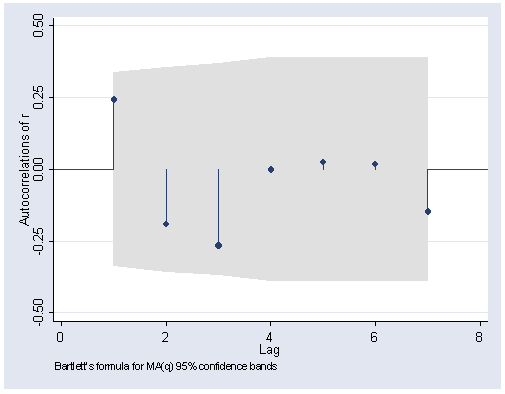
Figure 14.5 on page 382. The ac command produces a correlogram (the autocorrelations) with pointwise confidence intervals obtained from the Q statistic.
ac r, lags(7) yline(0) ylabel(-.5(.25).5)
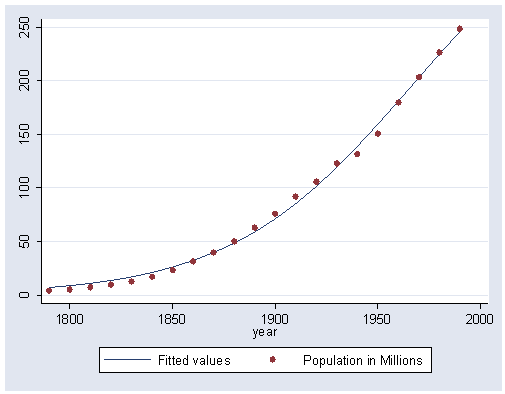
Figure 14.9 on page 400 using data file US-pop.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/US-pop, clear
(From Fox, Applied Regression Analysis. Use 'notes' command for source of data )
gen myear=year-1790
nl log3 pop myear, init(b1=350, b2=0.3, b3=15) /*nonlinear least squares using built-in model log3*/
(obs = 21)
Iteration 0: residual SS = 1312135
Iteration 1: residual SS = 100157.2
Iteration 2: residual SS = 88085.9
...more iterations in between....
Iteration 26: residual SS = 356.4
Iteration 27: residual SS = 356.4
Source | SS df MS Number of obs = 21
---------+------------------------------ F( 3, 18) = 4664.56
Model | 277074.795 3 92358.2651 Prob > F = 0.0000
Residual | 356.399974 18 19.7999986 R-squared = 0.9987
---------+------------------------------ Adj R-squared = 0.9985
Total | 277431.195 21 13211.0093 Root MSE = 4.449719
Res. dev. = 119.0576
3-parameter logistic function, pop=b1/(1+exp(-b2*(myear-b3)))
------------------------------------------------------------------------------
pop | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
b1 | 389.1659 30.8114 12.631 0.000 324.4335 453.8982
b2 | .022662 .0010857 20.873 0.000 .020381 .0249429
b3 | 176.0811 7.244577 24.305 0.000 160.8608 191.3014
------------------------------------------------------------------------------
(SE's, P values, CI's, and correlations are asymptotic approximations)
predict mpop if e(sample)
(option yhat assumed; fitted values)
graph twoway scatter mpop pop year, connect(l i) msymbol(i O)
predict res, r graph twoway scatter r year, yline(0) xlabel(1750(50)2000)
Table 14.8 on page 414 using the data file duncan.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/duncan, clear (From Fox, Applied Regression Analysis. Use 'notes' command for source of data )
Estimator: least squares.
regress prestige income educ
Source | SS df MS Number of obs = 45
---------+------------------------------ F( 2, 42) = 101.22
Model | 36180.9458 2 18090.4729 Prob > F = 0.0000
Residual | 7506.69865 42 178.73092 R-squared = 0.8282
---------+------------------------------ Adj R-squared = 0.8200
Total | 43687.6444 44 992.90101 Root MSE = 13.369
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
income | .5987328 .1196673 5.003 0.000 .3572343 .8402313
educ | .5458339 .0982526 5.555 0.000 .3475521 .7441158
_cons | -6.064663 4.271941 -1.420 0.163 -14.68579 2.556463
------------------------------------------------------------------------------
Estimator: least square*.
regress prestige income educ if(occtitle !="minister" & occtitle !="railroad_conductor")
Source | SS df MS Number of obs = 43
---------+------------------------------ F( 2, 40) = 141.26
Model | 36815.4292 2 18407.7146 Prob > F = 0.0000
Residual | 5212.57076 40 130.314269 R-squared = 0.8760
---------+------------------------------ Adj R-squared = 0.8698
Total | 42028.00 42 1000.66667 Root MSE = 11.416
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
income | .8673986 .1219756 7.111 0.000 .6208767 1.11392
educ | .3322408 .0987498 3.364 0.002 .1326599 .5318217
_cons | -6.408986 3.652627 -1.755 0.087 -13.79122 .9732494
------------------------------------------------------------------------------
Estimator: least absolute values.
qreg prestige income educ
Iteration 1: WLS sum of weighted deviations = 435.45438
Iteration 1: sum of abs. weighted deviations = 448.85635
Iteration 2: sum of abs. weighted deviations = 420.65054
Iteration 3: sum of abs. weighted deviations = 420.1346
Iteration 4: sum of abs. weighted deviations = 416.71435
Iteration 5: sum of abs. weighted deviations = 415.99351
Iteration 6: sum of abs. weighted deviations = 415.97706
Median regression Number of obs = 45
Raw sum of deviations 1249 (about 41)
Min sum of deviations 415.9771 Pseudo R2 = 0.6670
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
income | .7477064 .1016554 7.355 0.000 .5425576 .9528553
educ | .4587156 .0852699 5.380 0.000 .2866339 .6307972
_cons | -6.408257 4.068319 -1.575 0.123 -14.61846 1.801944
------------------------------------------------------------------------------
Estimator: Bisquare(biweight)
rreg prestige income educ, tolerance(0.0005)
Huber iteration 1: maximum difference in weights = .6047203
..more iterations...
Huber iteration 6: maximum difference in weights = .001508
Biweight iteration 7: maximum difference in weights = .28607984
..more iterations...
Biweight iteration 16: maximum difference in weights = .00046242
Robust regression estimates Number of obs = 45
F( 2, 42) = 141.84
Prob > F = 0.0000
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
income | .8183817 .1053366 7.769 0.000 .6058039 1.03096
educ | .4039986 .0864864 4.671 0.000 .229462 .5785352
_cons | -7.480399 3.760355 -1.989 0.053 -15.0691 .1083048
------------------------------------------------------------------------------
Estimator: Huber
We modified the rreg.ado file so it also displays the result from Huber estimation iterations. We call it https://stats.idre.ucla.edu/wp-content/uploads/2016/02/rregh.ado for Huber estimate.
rregh prestige income educ, tolerance(0.0005)
Huber iteration 1: maximum difference in weights = .6047203
Huber iteration 2: maximum difference in weights = .16902569
Huber iteration 3: maximum difference in weights = .04468015
Huber iteration 4: maximum difference in weights = .01946043
Huber iteration 5: maximum difference in weights = .00284761
Huber iteration 6: maximum difference in weights = .001508
Huber iteration 7: maximum difference in weights = .00041577
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
income | .7101061 .1021612 6.95 0.000 .5039364 .9162758
educ | .48201 .0836081 5.77 0.000 .313282 .650738
_cons | -7.283356 3.32942 -2.19 0.034 -14.0024 -.5643149
------------------------------------------------------------------------------
Biweight iteration 8: maximum difference in weights = .28604323
Biweight iteration 9: maximum difference in weights = .09851044
Biweight iteration 10: maximum difference in weights = .15075821
Biweight iteration 11: maximum difference in weights = .07122389
Biweight iteration 12: maximum difference in weights = .02099558
Biweight iteration 13: maximum difference in weights = .01118912
Biweight iteration 14: maximum difference in weights = .00423083
Biweight iteration 15: maximum difference in weights = .00229196
Biweight iteration 16: maximum difference in weights = .00086014
Biweight iteration 17: maximum difference in weights = .00046868
Robust regression Number of obs = 45
F( 2, 42) = 141.84
Prob > F = 0.0000
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
income | .8183817 .1053366 7.77 0.000 .6058038 1.03096
educ | .4039985 .0864864 4.67 0.000 .2294619 .5785352
_cons | -7.480396 3.760356 -1.99 0.053 -15.0691 .1083092
------------------------------------------------------------------------------
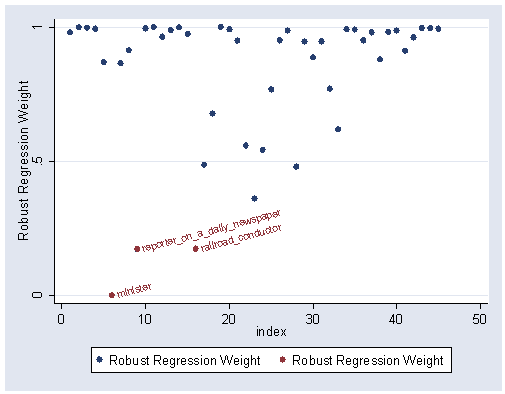
Figure 14.14 on page 415 on final weights for the bisquare estimator.
rreg prestige income educ, tolerance(.0005) genwt(mywt) /*generating weights (intermediate output omitted here.) gen index=_n graph twoway (scatter mywt index) /// (scatter mywt index if mywt <= .25, mlabel(occtitle) mlabangle(15)), ylabel(0 .5 1)
Figure 14.15 on page 418 using the data file prestige.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/prestige, clear (From Fox, Applied Regression Analysis. Use 'notes' command for source of data) sort income gen neb = abs(income-income[80]) /*get obs close to income[80]*/ sort neb gen mpr =prestige in 1/40 (62 missing values generated) gen minc= income in 1/40 /*get x-coordinate for reference line */ (62 missing values generated) display minc[1] 8403 display minc[40] 5902
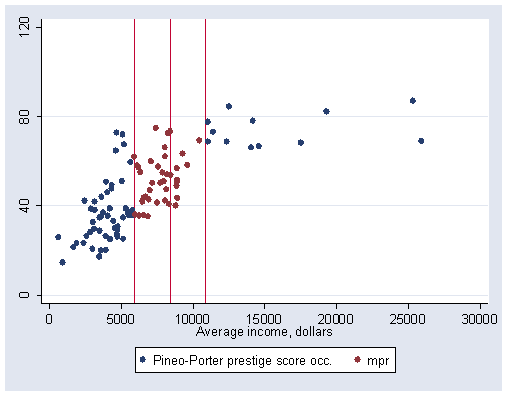
Figure 14.15 (a) on page 418 using symmetric neighborhood. For example, to get the upper bound we do (8403+(8403-5902))=10904.
graph twoway (scatter prestige income) (scatter mpr income), /// xline(5902 8403 10904) xlabel(0(5000)30000) ylabel(0(40)120)
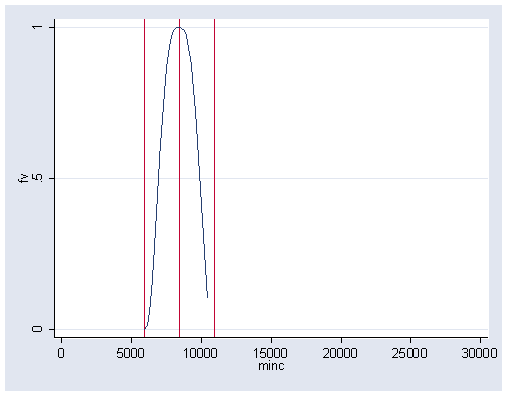
Figure 14.15 (b) on page 418 using tricube weight function.
gen stinc=abs(minc-8403)/2501 (62 missing values generated) gen fv=(1-abs(stinc)^3)^3 (62 missing values generated) replace fv=0 if (fv<0) (0 real changes made) sort minc graph twoway scatter fv minc, connect(l) msymbol(i) /// xline(5902 8403 10904) xlabel(0(5000)30000) ylabel(0 .5 1)
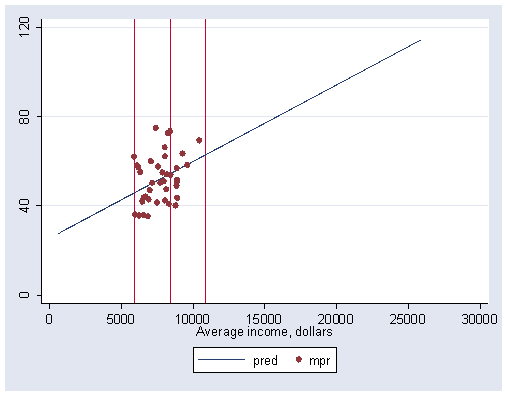
Figure 14.15 (c) on page 418 showing local weighted regression.
regress prestige minc
(output omitted here.)
matrix list e(b)
e(b)[1,2]
minc _cons
y1 .00343774 25.4807
gen pred=25.4807+.00343774 *income
graph twoway scatter pred mpr income, connect(l) msymbol(i O) ///
xline(5902 8403 10904) xlabel(0(5000)30000) ylabel(0(40)120)
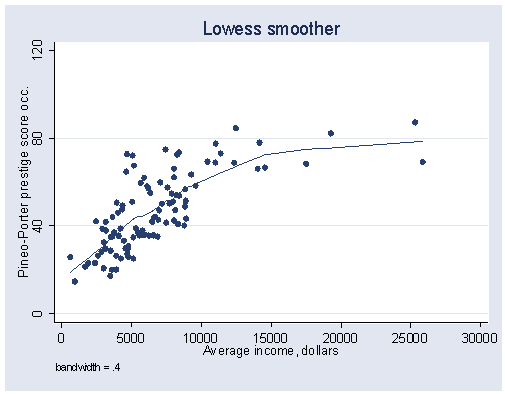
Figure 14.15 (d) on page 418 on lowess smoothing.
lowess prestige income, bwidth(0.4) xlabel(0(5000)30000) ylabel(0(40)120)
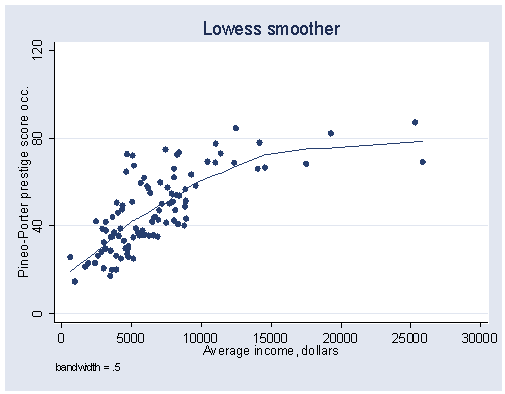
Figure 14.16 on page 421.
lowess prestige income, bwidth(0.5) xlabel(0(5000)30000) ylabel(0(40)120) gen(newp)
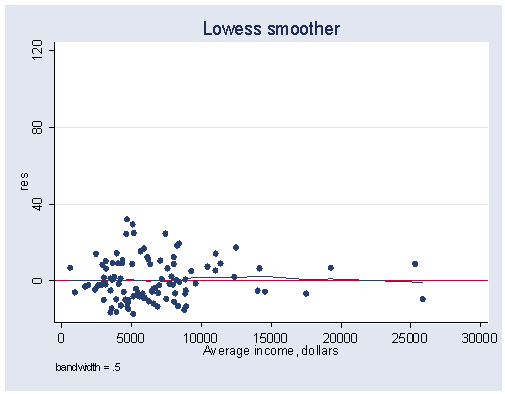
gen res=prestige-newp lowess res income, bwidth(0.5) xlabel(0(5000)30000) ylabel(0(40)120) yline(0)
For calculation on page 423 and Figure 14.17 on page 424, please see the SAS version of this page. SAS does it simply with proc loess.