Version info: Code for this page was tested in Stata 12.
Introduction
This page shows how to perform a number of statistical tests using Stata. Each section gives a brief description of the aim of the statistical test, when it is used, an example showing the Stata commands and Stata output with a brief interpretation of the output. You can see the page Choosing the Correct Statistical Test for a table that shows an overview of when each test is appropriate to use. In deciding which test is appropriate to use, it is important to consider the type of variables that you have (i.e., whether your variables are categorical, ordinal or interval and whether they are normally distributed), see What is the difference between categorical, ordinal and interval variables? for more information on this.
About the hsb data file
Most of the examples in this page will use a data file called hsb2, high school and beyond. This data file contains 200 observations from a sample of high school students with demographic information about the students, such as their gender (female), socio-economic status (ses) and ethnic background (race). It also contains a number of scores on standardized tests, including tests of reading (read), writing (write), mathematics (math) and social studies (socst). You can get the hsb2 data file from within Stata by typing:
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2
One sample t-test
A one sample t-test allows us to test whether a sample mean (of a normally distributed interval variable) significantly differs from a hypothesized value. For example, using the hsb2 data file, say we wish to test whether the average writing score (write) differs significantly from 50. We can do this as shown below.
ttest write=50
One-sample t test
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
write | 200 52.775 .6702372 9.478586 51.45332 54.09668
------------------------------------------------------------------------------
Degrees of freedom: 199
Ho: mean(write) = 50
Ha: mean < 50 Ha: mean ~= 50 Ha: mean > 50
t = 4.1403 t = 4.1403 t = 4.1403
P < t = 1.0000 P > |t| = 0.0001 P > t = 0.0000
The mean of the variable write for this particular sample of students is 52.775, which is statistically significantly different from the test value of 50. We would conclude that this group of students has a significantly higher mean on the writing test than 50.
See also
One sample median test
A one sample median test allows us to test whether a sample median differs significantly from a hypothesized value. We will use the same variable, write, as we did in the one sample t-test example above, but we do not need to assume that it is interval and normally distributed (we only need to assume that write is an ordinal variable and that its distribution is symmetric). We will test whether the median writing score (write) differs significantly from 50.
signrank write=50
Wilcoxon signed-rank test
sign | obs sum ranks expected
-------------+---------------------------------
positive | 126 13429 10048.5
negative | 72 6668 10048.5
zero | 2 3 3
-------------+---------------------------------
all | 200 20100 20100
unadjusted variance 671675.00
adjustment for ties -1760.25
adjustment for zeros -1.25
---------
adjusted variance 669913.50
Ho: write = 50
z = 4.130
Prob > |z| = 0.0000
The results indicate that the median of the variable write for this group is statistically significantly different from 50.
See also
Binomial test
A one sample binomial test allows us to test whether the proportion of successes on a two-level categorical dependent variable significantly differs from a hypothesized value. For example, using the hsb2 data file, say we wish to test whether the proportion of females (female) differs significantly from 50%, i.e., from .5. We can do this as shown below.
bitest female=.5
Variable | N Observed k Expected k Assumed p Observed p
-------------+------------------------------------------------------------
female | 200 109 100 0.50000 0.54500
Pr(k >= 109) = 0.114623 (one-sided test)
Pr(k <= 109) = 0.910518 (one-sided test)
Pr(k <= 91 or k >= 109) = 0.229247 (two-sided test)
The results indicate that there is no statistically significant difference (p = .2292). In other words, the proportion of females does not significantly differ from the hypothesized value of 50%.
See also
Chi-square goodness of fit
A chi-square goodness of fit test allows us to test whether the observed proportions for a categorical variable differ from hypothesized proportions. For example, let’s suppose that we believe that the general population consists of 10% Hispanic, 10% Asian, 10% African American and 70% White folks. We want to test whether the observed proportions from our sample differ significantly from these hypothesized proportions. To conduct the chi-square goodness of fit test, you need to first download the csgof program that performs this test. You can download csgof from within Stata by typing search csgof (see How can I used the search command to search for programs and get additional help? for more information about using search).
Now that the csgof program is installed, we can use it by typing:
csgof race, expperc(10 10 10 70)
race expperc expfreq obsfreq
hispanic 10 20 24
asian 10 20 11
african-amer 10 20 20
white 70 140 145
chisq(3) is 5.03, p = .1697
These results show that racial composition in our sample does not differ significantly from the hypothesized values that we supplied (chi-square with three degrees of freedom = 5.03, p = .1697).
See also
Two independent samples t-test
An independent samples t-test is used when you want to compare the means of a normally distributed interval dependent variable for two independent groups. For example, using the hsb2 data file, say we wish to test whether the mean for write is the same for males and females.
ttest write, by(female)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
male | 91 50.12088 1.080274 10.30516 47.97473 52.26703
female | 109 54.99083 .7790686 8.133715 53.44658 56.53507
---------+--------------------------------------------------------------------
combined | 200 52.775 .6702372 9.478586 51.45332 54.09668
---------+--------------------------------------------------------------------
diff | -4.869947 1.304191 -7.441835 -2.298059
------------------------------------------------------------------------------
Degrees of freedom: 198
Ho: mean(male) - mean(female) = diff = 0
Ha: diff < 0 Ha: diff ~= 0 Ha: diff > 0
t = -3.7341 t = -3.7341 t = -3.7341
P < t = 0.0001 P > |t| = 0.0002 P > t = 0.9999
The results indicate that there is a statistically significant difference between the mean writing score for males and females (t = -3.7341, p = .0002). In other words, females have a statistically significantly higher mean score on writing (54.99) than males (50.12).
See also
Wilcoxon-Mann-Whitney test
The Wilcoxon-Mann-Whitney test is a non-parametric analog to the independent samples t-test and can be used when you do not assume that the dependent variable is a normally distributed interval variable (you only assume that the variable is at least ordinal). You will notice that the Stata syntax for the Wilcoxon-Mann-Whitney test is almost identical to that of the independent samples t-test. We will use the same data file (the hsb2 data file) and the same variables in this example as we did in the independent t-test example above and will not assume that write, our dependent variable, is normally distributed.
ranksum write, by(female)
Two-sample Wilcoxon rank-sum (Mann-Whitney) test
female | obs rank sum expected
-------------+---------------------------------
male | 91 7792 9145.5
female | 109 12308 10954.5
-------------+---------------------------------
combined | 200 20100 20100
unadjusted variance 166143.25
adjustment for ties -852.96
----------
adjusted variance 165290.29
Ho: write(female==male) = write(female==female)
z = -3.329
Prob > |z| = 0.0009
The results suggest that there is a statistically significant difference between the underlying distributions of the write scores of males and the write scores of females (z = -3.329, p = 0.0009). You can determine which group has the higher rank by looking at the how the actual rank sums compare to the expected rank sums under the null hypothesis. The sum of the female ranks was higher while the sum of the male ranks was lower. Thus the female group had higher rank.
See also
- FAQ: Why is the Mann-Whitney significant when the medians are equal?
- Stata Class Notes: Analyzing Data
Chi-square test
A chi-square test is used when you want to see if there is a relationship between two categorical variables. In Stata, the chi2 option is used with the tabulate command to obtain the test statistic and its associated p-value. Using the hsb2 data file, let’s see if there is a relationship between the type of school attended (schtyp) and students’ gender (female). Remember that the chi-square test assumes the expected value of each cell is five or higher. This assumption is easily met in the examples below. However, if this assumption is not met in your data, please see the section on Fisher’s exact test below.
tabulate schtyp female, chi2
type of | female
school | male female | Total
-----------+----------------------+----------
public | 77 91 | 168
private | 14 18 | 32
-----------+----------------------+----------
Total | 91 109 | 200
Pearson chi2(1) = 0.0470 Pr = 0.828
These results indicate that there is no statistically significant relationship between the type of school attended and gender (chi-square with one degree of freedom = 0.0470, p = 0.828).
Let’s look at another example, this time looking at the relationship between gender (female) and socio-economic status (ses). The point of this example is that one (or both) variables may have more than two levels, and that the variables do not have to have the same number of levels. In this example, female has two levels (male and female) and ses has three levels (low, medium and high).
tabulate female ses, chi2
| ses
female | low middle high | Total
-----------+---------------------------------+----------
male | 15 47 29 | 91
female | 32 48 29 | 109
-----------+---------------------------------+----------
Total | 47 95 58 | 200
Pearson chi2(2) = 4.5765 Pr = 0.101
Again we find that there is no statistically significant relationship between the variables (chi-square with two degrees of freedom = 4.5765, p = 0.101).
See also
- Stata Learning Module: A Statistical Sampler in Stata
- Stata Teaching Tools: Probability Tables
- Stata Teaching Tools: Chi-squared distribution
- Stata Textbook Examples: An Introduction to Categorical Analysis, Chapter 2
Fisher’s exact test
The Fisher’s exact test is used when you want to conduct a chi-square test, but one or more of your cells has an expected frequency of five or less. Remember that the chi-square test assumes that each cell has an expected frequency of five or more, but the Fisher’s exact test has no such assumption and can be used regardless of how small the expected frequency is. In the example below, we have cells with observed frequencies of two and one, which may indicate expected frequencies that could be below five, so we will use Fisher’s exact test with the exact option on the tabulate command.
tabulate schtyp race, exact
type of | race
school | hispanic asian african-a white | Total
-----------+--------------------------------------------+----------
public | 22 10 18 118 | 168
private | 2 1 2 27 | 32
-----------+--------------------------------------------+----------
Total | 24 11 20 145 | 200
Fisher's exact = 0.597
These results suggest that there is not a statistically significant relationship between race and type of school (p = 0.597). Note that the Fisher’s exact test does not have a “test statistic”, but computes the p-value directly.
See also
- Stata Learning Module: A Statistical Sampler in Stata
- Stata Textbook Examples: Statistical Methods for the Social Sciences, Chapter 7
One-way ANOVA
A one-way analysis of variance (ANOVA) is used when you have a categorical independent variable (with two or more categories) and a normally distributed interval dependent variable and you wish to test for differences in the means of the dependent variable broken down by the levels of the independent variable. For example, using the hsb2 data file, say we wish to test whether the mean of write differs between the three program types (prog). The command for this test would be:
anova write prog
Number of obs = 200 R-squared = 0.1776
Root MSE = 8.63918 Adj R-squared = 0.1693
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 3175.69786 2 1587.84893 21.27 0.0000
|
prog | 3175.69786 2 1587.84893 21.27 0.0000
|
Residual | 14703.1771 197 74.635417
-----------+----------------------------------------------------
Total | 17878.875 199 89.843593
The mean of the dependent variable differs significantly among the levels of program type. However, we do not know if the difference is between only two of the levels or all three of the levels. (The F test for the Model is the same as the F test for prog because prog was the only variable entered into the model. If other variables had also been entered, the F test for the Model would have been different from prog.) To see the mean of write for each level of program type, you can use the tabulate command with the summarize option, as illustrated below.
tabulate prog, summarize(write)
type of | Summary of writing score
program | Mean Std. Dev. Freq.
------------+------------------------------------
general | 51.333333 9.3977754 45
academic | 56.257143 7.9433433 105
vocation | 46.76 9.3187544 50
------------+------------------------------------
Total | 52.775 9.478586 200
From this we can see that the students in the academic program have the highest mean writing score, while students in the vocational program have the lowest.
See also
- Design and Analysis: A Researchers Handbook Third Edition by Geoffrey Keppel
- Stata Frequently Asked Questions
- Stata Programs for Data Analysis
Kruskal Wallis test
The Kruskal Wallis test is used when you have one independent variable with two or more levels and an ordinal dependent variable. In other words, it is the non-parametric version of ANOVA and a generalized form of the Mann-Whitney test method since it permits 2 or more groups. We will use the same data file as the one way ANOVA example above (the hsb2 data file) and the same variables as in the example above, but we will not assume that write is a normally distributed interval variable.
kwallis write, by(prog)
Test: Equality of populations (Kruskal-Wallis test)
prog _Obs _RankSum
general < 45 4079.00
academic 105 12764.00
vocation 50 3257.00
chi-squared = 33.870 with 2 d.f.
probability = 0.0001
chi-squared with ties = 34.045 with 2 d.f.
probability = 0.0001
If some of the scores receive tied ranks, then a correction factor is used, yielding a slightly different value of chi-squared. With or without ties, the results indicate that there is a statistically significant difference among the three type of programs.
Paired t-test
A paired (samples) t-test is used when you have two related observations (i.e. two observations per subject) and you want to see if the means on these two normally distributed interval variables differ from one another. For example, using the hsb2 data file we will test whether the mean of read is equal to the mean of write.
ttest read = write
Paired t test
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | 200 52.23 .7249921 10.25294 50.80035 53.65965
write | 200 52.775 .6702372 9.478586 51.45332 54.09668
---------+--------------------------------------------------------------------
diff | 200 -.545 .6283822 8.886666 -1.784142 .6941424
------------------------------------------------------------------------------
Ho: mean(read - write) = mean(diff) = 0
Ha: mean(diff) < 0 Ha: mean(diff) ~= 0 Ha: mean(diff) > 0
t = -0.8673 t = -0.8673 t = -0.8673
P < t = 0.1934 P > |t| = 0.3868 P > t = 0.8066
These results indicate that the mean of read is not statistically significantly different from the mean of write (t = -0.8673, p = 0.3868).
See also
Wilcoxon signed rank sum test
The Wilcoxon signed rank sum test is the non-parametric version of a paired samples t-test. You use the Wilcoxon signed rank sum test when you do not wish to assume that the difference between the two variables is interval and normally distributed (but you do assume the difference is ordinal). We will use the same example as above, but we will not assume that the difference between read and write is interval and normally distributed.
signrank read = write
Wilcoxon signed-rank test
sign | obs sum ranks expected
-------------+---------------------------------
positive | 88 9264 9990
negative | 97 10716 9990
zero | 15 120 120
-------------+---------------------------------
all | 200 20100 20100
unadjusted variance 671675.00
adjustment for ties -715.25
adjustment for zeros -310.00
----------
adjusted variance 670649.75
Ho: read = write
z = -0.887
Prob > |z| = 0.3753
The results suggest that there is not a statistically significant difference between read and write.
If you believe the differences between read and write were not ordinal but could merely be classified as positive and negative, then you may want to consider a sign test in lieu of sign rank test. Again, we will use the same variables in this example and assume that this difference is not ordinal.
signtest read = write
Sign test
sign | observed expected
-------------+------------------------
positive | 88 92.5
negative | 97 92.5
zero | 15 15
-------------+------------------------
all | 200 200
One-sided tests:
Ho: median of read - write = 0 vs.
Ha: median of read - write > 0
Pr(#positive >= 88) =
Binomial(n = 185, x >= 88, p = 0.5) = 0.7688
Ho: median of read - write = 0 vs.
Ha: median of read - write < 0
Pr(#negative >= 97) =
Binomial(n = 185, x >= 97, p = 0.5) = 0.2783
Two-sided test:
Ho: median of read - write = 0 vs.
Ha: median of read - write ~= 0
Pr(#positive >= 97 or #negative >= 97) =
min(1, 2*Binomial(n = 185, x >= 97, p = 0.5)) = 0.5565
This output gives both of the one-sided tests as well as the two-sided test. Assuming that we were looking for any difference, we would use the two-sided test and conclude that no statistically significant difference was found (p=.5565).
See also
McNemar test
You would perform McNemar’s test if you were interested in the marginal frequencies of two binary outcomes. These binary outcomes may be the same outcome variable on matched pairs (like a case-control study) or two outcome variables from a single group. For example, let us consider two questions, Q1 and Q2, from a test taken by 200 students. Suppose 172 students answered both questions correctly, 15 students answered both questions incorrectly, 7 answered Q1 correctly and Q2 incorrectly, and 6 answered Q2 correctly and Q1 incorrectly. These counts can be considered in a two-way contingency table. The null hypothesis is that the two questions are answered correctly or incorrectly at the same rate (or that the contingency table is symmetric). We can enter these counts into Stata using mcci, a command from Stata’s epidemiology tables. The outcome is labeled according to case-control study conventions.
mcci 172 6 7 15
| Controls |
Cases | Exposed Unexposed | Total
-----------------+------------------------+------------
Exposed | 172 6 | 178
Unexposed | 7 15 | 22
-----------------+------------------------+------------
Total | 179 21 | 200
McNemar's chi2(1) = 0.08 Prob > chi2 = 0.7815
Exact McNemar significance probability = 1.0000
Proportion with factor
Cases .89
Controls .895 [95% Conf. Interval]
--------- --------------------
difference -.005 -.045327 .035327
ratio .9944134 .9558139 1.034572
rel. diff. -.047619 -.39205 .2968119
odds ratio .8571429 .2379799 2.978588 (exact)
McNemar’s chi-square statistic suggests that there is not a statistically significant difference in the proportions of correct/incorrect answers to these two questions.
One-way repeated measures ANOVA
You would perform a one-way repeated measures analysis of variance if you had one categorical independent variable and a normally distributed interval dependent variable that was repeated at least twice for each subject. This is the equivalent of the paired samples t-test, but allows for two or more levels of the categorical variable. This tests whether the mean of the dependent variable differs by the categorical variable. We have an example data set called rb4, which is used in Kirk’s book Experimental Design. In this data set, y is the dependent variable, a is the repeated measure and s is the variable that indicates the subject number.
use https://stats.idre.ucla.edu/stat/stata/examples/kirk/rb4 anova y a s, repeated(a)
Number of obs = 32 R-squared = 0.7318
Root MSE = 1.18523 Adj R-squared = 0.6041
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 80.50 10 8.05 5.73 0.0004
|
a | 49.00 3 16.3333333 11.63 0.0001
s | 31.50 7 4.50 3.20 0.0180
|
Residual | 29.50 21 1.4047619
-----------+----------------------------------------------------
Total | 110.00 31 3.5483871
Between-subjects error term: s
Levels: 8 (7 df)
Lowest b.s.e. variable: s
Repeated variable: a
Huynh-Feldt epsilon = 0.8343
Greenhouse-Geisser epsilon = 0.6195
Box's conservative epsilon = 0.3333
------------ Prob > F ------------
Source | df F Regular H-F G-G Box
-----------+----------------------------------------------------
a | 3 11.63 0.0001 0.0003 0.0015 0.0113
Residual | 21
-----------+----------------------------------------------------
You will notice that this output gives four different p-values. The “regular” (0.0001) is the p-value that you would get if you assumed compound symmetry in the variance-covariance matrix. Because that assumption is often not valid, the three other p-values offer various corrections (the Huynh-Feldt, H-F, Greenhouse-Geisser, G-G and Box’s conservative, Box). No matter which p-value you use, our results indicate that we have a statistically significant effect of a at the .05 level.
See also
- Stata FAQ: How can I test for nonadditivity in a randomized block ANOVA in Stata?
- Stata Textbook Examples, Experimental Design, Chapter 7
- Stata Code Fragment: ANOVA
Repeated measures logistic regression
If you have a binary outcome measured repeatedly for each subject and you wish to run a logistic regression that accounts for the effect of these multiple measures from each subjects, you can perform a repeated measures logistic regression. In Stata, this can be done using the xtgee command and indicating binomial as the probability distribution and logit as the link function to be used in the model. The exercise data file contains 3 pulse measurements of 30 people assigned to 2 different diet regiments and 3 different exercise regiments. If we define a “high” pulse as being over 100, we can then predict the probability of a high pulse using diet regiment.
First, we use xtset to define which variable defines the repetitions. In this dataset, there are three measurements taken for each id, so we will use id as our panel variable. Then we can use i: before diet so that we can create indicator variables as needed.
use https://stats.idre.ucla.edu/stat/stata/whatstat/exercise, clear xtset id xtgee highpulse i.diet, family(binomial) link(logit)
Iteration 1: tolerance = 1.753e-08
GEE population-averaged model Number of obs = 90
Group variable: id Number of groups = 30
Link: logit Obs per group: min = 3
Family: binomial avg = 3.0
Correlation: exchangeable max = 3
Wald chi2(1) = 1.53
Scale parameter: 1 Prob > chi2 = 0.2157
------------------------------------------------------------------------------
highpulse | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
2.diet | .7537718 .6088196 1.24 0.216 -.4394927 1.947036
_cons | -1.252763 .4621704 -2.71 0.007 -2.1586 -.3469257
------------------------------------------------------------------------------
These results indicate that diet is not statistically significant (Z = 1.24, p = 0.216).
Factorial ANOVA
A factorial ANOVA has two or more categorical independent variables (either with or without the interactions) and a single normally distributed interval dependent variable. For example, using the hsb2 data file we will look at writing scores (write) as the dependent variable and gender (female) and socio-economic status (ses) as independent variables, and we will include an interaction of female by ses. Note that in Stata, you do not need to have the interaction term(s) in your data set. Rather, you can have Stata create it/them temporarily by placing an asterisk between the variables that will make up the interaction term(s).
anova write female ses female##ses
Number of obs = 200 R-squared = 0.1274
Root MSE = 8.96748 Adj R-squared = 0.1049
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 2278.24419 5 455.648837 5.67 0.0001
|
female | 1334.49331 1 1334.49331 16.59 0.0001
ses | 1063.2527 2 531.626349 6.61 0.0017
female#ses | 21.4309044 2 10.7154522 0.13 0.8753
|
Residual | 15600.6308 194 80.4156228
-----------+----------------------------------------------------
Total | 17878.875 199 89.843593
These results indicate that the overall model is statistically significant (F = 5.67, p = 0.001). The variables female and ses are also statistically significant (F = 16.59, p = 0.0001 and F = 6.61, p = 0.0017, respectively). However, that interaction between female and ses is not statistically significant (F = 0.13, p = 0.8753).
See also
- Stata Frequently Asked Questions
- Stata Textbook Examples, Experimental Design, Chapter 9
- Stata Code Fragment: ANOVA
Friedman test
You perform a Friedman test when you have one within-subjects independent variable with two or more levels and a dependent variable that is not interval and normally distributed (but at least ordinal). We will use this test to determine if there is a difference in the reading, writing and math scores. The null hypothesis in this test is that the distribution of the ranks of each type of score (i.e., reading, writing and math) are the same. To conduct the Friedman test in Stata, you need to first download the friedman program that performs this test. You can download friedman from within Stata by typing search friedman (see How can I used the search command to search for programs and get additional help? for more information about using search). Also, your data will need to be transposed such that subjects are the columns and the variables are the rows. We will use the xpose command to arrange our data this way.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2 keep read write math xpose, clear friedman v1-v200
Friedman = 0.6175 Kendall = 0.0015 P-value = 0.7344
Friedman’s chi-square has a value of 0.6175 and a p-value of 0.7344 and is not statistically significant. Hence, there is no evidence that the distributions of the three types of scores are different.
Ordered logistic regression
Ordered logistic regression is used when the dependent variable is ordered, but not continuous. For example, using the hsb2 data file we will create an ordered variable called write3. This variable will have the values 1, 2 and 3, indicating a low, medium or high writing score. We do not generally recommend categorizing a continuous variable in this way; we are simply creating a variable to use for this example. We will use gender (female), reading score (read) and social studies score (socst) as predictor variables in this model.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2 generate write3 = 1 replace write3 = 2 if write >= 49 & write <= 57 replace write3 = 3 if write >= 58 & write <= 70
ologit write3 female read socst
Iteration 0: log likelihood = -218.31357
Iteration 1: log likelihood = -157.692
Iteration 2: log likelihood = -156.28133
Iteration 3: log likelihood = -156.27632
Iteration 4: log likelihood = -156.27632
Ordered logistic regression Number of obs = 200
LR chi2(3) = 124.07
Prob > chi2 = 0.0000
Log likelihood = -156.27632 Pseudo R2 = 0.2842
------------------------------------------------------------------------------
write3 | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | 1.285435 .3244567 3.96 0.000 .6495115 1.921359
read | .1177202 .0213565 5.51 0.000 .0758623 .1595781
socst | .0801873 .0194432 4.12 0.000 .0420794 .1182952
-------------+----------------------------------------------------------------
/cut1 | 9.703706 1.197002 7.357626 12.04979
/cut2 | 11.8001 1.304306 9.243705 14.35649
------------------------------------------------------------------------------
The results indicate that the overall model is statistically significant (p < .0000), as are each of the predictor variables (p < .000). There are two cutpoints for this model because there are three levels of the outcome variable.
One of the assumptions underlying ordinal logistic (and ordinal probit) regression is that the relationship between each pair of outcome groups is the same. In other words, ordinal logistic regression assumes that the coefficients that describe the relationship between, say, the lowest versus all higher categories of the response variable are the same as those that describe the relationship between the next lowest category and all higher categories, etc. This is called the proportional odds assumption or the parallel regression assumption. Because the relationship between all pairs of groups is the same, there is only one set of coefficients (only one model). If this was not the case, we would need different models (such as a generalized ordered logit model) to describe the relationship between each pair of outcome groups. To test this assumption, we can use either the omodel command (search omodel, see How can I used the search command to search for programs and get additional help? for more information about using search) or the brant command. We will show both below.
omodel logit write3 female read socst
Iteration 0: log likelihood = -218.31357
Iteration 1: log likelihood = -158.87444
Iteration 2: log likelihood = -156.35529
Iteration 3: log likelihood = -156.27644
Iteration 4: log likelihood = -156.27632
Ordered logit estimates Number of obs = 200
LR chi2(3) = 124.07
Prob > chi2 = 0.0000
Log likelihood = -156.27632 Pseudo R2 = 0.2842
------------------------------------------------------------------------------
write3 | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | 1.285435 .3244565 3.96 0.000 .649512 1.921358
read | .1177202 .0213564 5.51 0.000 .0758623 .159578
socst | .0801873 .0194432 4.12 0.000 .0420794 .1182952
-------------+----------------------------------------------------------------
_cut1 | 9.703706 1.197 (Ancillary parameters)
_cut2 | 11.8001 1.304304
------------------------------------------------------------------------------
Approximate likelihood-ratio test of proportionality of odds
across response categories:
chi2(3) = 2.03
Prob > chi2 = 0.5658
brant, detail
Estimated coefficients from j-1 binary regressions
y>1 y>2
female 1.5673604 1.0629714
read .11712422 .13401723
socst .0842684 .06429241
_cons -10.001584 -11.671854
Brant Test of Parallel Regression Assumption
Variable | chi2 p>chi2 df
-------------+--------------------------
All | 2.07 0.558 3
-------------+--------------------------
female | 1.08 0.300 1
read | 0.26 0.608 1
socst | 0.52 0.470 1
----------------------------------------
A significant test statistic provides evidence that the parallel
regression assumption has been violated.
Both of these tests indicate that the proportional odds assumption has not been violated.
See also
- Stata FAQ: In ordered probit and logit, what are the cut points?
- Stata Annotated Output: Ordered logistic regression
Factorial logistic regression
A factorial logistic regression is used when you have two or more categorical independent variables but a dichotomous dependent variable. For example, using the hsb2 data file we will use female as our dependent variable, because it is the only dichotomous (0/1) variable in our data set; certainly not because it common practice to use gender as an outcome variable. We will use type of program (prog) and school type (schtyp) as our predictor variables. Because prog is a categorical variable (it has three levels), we need to create dummy codes for it. The use of i.prog does this. You can use the logit command if you want to see the regression coefficients or the logistic command if you want to see the odds ratios.
logit female i.prog##schtyp
Iteration 0: log likelihood = -137.81834
Iteration 1: log likelihood = -136.25886
Iteration 2: log likelihood = -136.24502
Iteration 3: log likelihood = -136.24501
Logistic regression Number of obs = 200
LR chi2(5) = 3.15
Prob > chi2 = 0.6774
Log likelihood = -136.24501 Pseudo R2 = 0.0114
------------------------------------------------------------------------------
female | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog |
2 | .3245866 .3910782 0.83 0.407 -.4419125 1.091086
3 | .2183474 .4319116 0.51 0.613 -.6281839 1.064879
|
2.schtyp | 1.660724 1.141326 1.46 0.146 -.5762344 3.897683
|
prog#schtyp |
2 2 | -1.934018 1.232722 -1.57 0.117 -4.350108 .4820729
3 2 | -1.827778 1.840256 -0.99 0.321 -5.434614 1.779057
|
_cons | -.0512933 .3203616 -0.16 0.873 -.6791906 .576604
------------------------------------------------------------------------------
The results indicate that the overall model is not statistically significant (LR chi2 = 3.15, p = 0.6774). Furthermore, none of the coefficients are statistically significant either. We can use the test command to get the test of the overall effect of prog as shown below. This shows that the overall effect of prog is not statistically significant.
test 2.prog 3.prog
( 1) [female]2.prog = 0
( 2) [female]3.prog = 0
chi2( 2) = 0.69
Prob > chi2 = 0.7086
Likewise, we can use the testparm command to get the test of the overall effect of the prog by schtyp interaction, as shown below. This shows that the overall effect of this interaction is not statistically significant.
testparm prog#schtyp
( 1) [female]2.prog#2.schtyp = 0
( 2) [female]3.prog#2.schtyp = 0
chi2( 2) = 2.47
Prob > chi2 = 0.2902
If you prefer, you could use the logistic command to see the results as odds ratios, as shown below.
logistic female i.prog##schtyp
Logistic regression Number of obs = 200
LR chi2(5) = 3.15
Prob > chi2 = 0.6774
Log likelihood = -136.24501 Pseudo R2 = 0.0114
------------------------------------------------------------------------------
female | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog |
2 | 1.383459 .5410405 0.83 0.407 .6428059 2.977505
3 | 1.244019 .5373063 0.51 0.613 .5335599 2.900487
|
2.schtyp | 5.263121 6.006939 1.46 0.146 .5620107 49.28811
|
prog#schtyp |
2 2 | .1445662 .1782099 -1.57 0.117 .0129054 1.619428
3 2 | .1607704 .2958586 -0.99 0.321 .0043629 5.924268
------------------------------------------------------------------------------
Correlation
A correlation is useful when you want to see the linear relationship between two (or more) normally distributed interval variables. For example, using the hsb2 data file we can run a correlation between two continuous variables, read and write.
corr read write
(obs=200)
| read write
-------------+------------------
read | 1.0000
write | 0.5968 1.0000
In the second example, we will run a correlation between a dichotomous variable, female, and a continuous variable, write. Although it is assumed that the variables are interval and normally distributed, we can include dummy variables when performing correlations.
corr female write
(obs=200)
| female write
-------------+------------------
female | 1.0000
write | 0.2565 1.0000
In the first example above, we see that the correlation between read and write is 0.5968. By squaring the correlation and then multiplying by 100, you can determine what percentage of the variability is shared. Let’s round 0.5968 to be 0.6, which when squared would be .36, multiplied by 100 would be 36%. Hence read shares about 36% of its variability with write. In the output for the second example, we can see the correlation between write and female is 0.2565. Squaring this number yields .06579225, meaning that female shares approximately 6.5% of its variability with write.
See also
- Annotated Stata Output: Correlation
- Stata Teaching Tools
- Stata Learning Module: A Statistical Sampler in Stata
- Stata Programs for Data Analysis
- Stata Class Notes: Exploring Data
- Stata Class Notes: Analyzing Data
Simple linear regression
Simple linear regression allows us to look at the linear relationship between one normally distributed interval predictor and one normally distributed interval outcome variable. For example, using the hsb2 data file, say we wish to look at the relationship between writing scores (write) and reading scores (read); in other words, predicting write from read.
regress write read
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .5517051 .0527178 10.47 0.000 .4477446 .6556656
_cons | 23.95944 2.805744 8.54 0.000 18.42647 29.49242
------------------------------------------------------------------------------
We see that the relationship between write and read is positive (.5517051) and based on the t-value (10.47) and p-value (0.000), we would conclude this relationship is statistically significant. Hence, we would say there is a statistically significant positive linear relationship between reading and writing.
See also
- Regression With Stata: Chapter 1 – Simple and Multiple Regression
- Stata Annotated Output: Regression
- Stata Frequently Asked Questions
- Stata Textbook Examples: Regression with Graphics, Chapter 2
- Stata Textbook Examples: Applied Regression Analysis, Chapter 5
Non-parametric correlation
A Spearman correlation is used when one or both of the variables are not assumed to be normally distributed and interval (but are assumed to be ordinal). The values of the variables are converted in ranks and then correlated. In our example, we will look for a relationship between read and write. We will not assume that both of these variables are normal and interval .
spearman read write
Number of obs = 200
Spearman's rho = 0.6167
Test of Ho: read and write are independent
Prob > |t| = 0.0000
The results suggest that the relationship between read and write (rho = 0.6167, p = 0.000) is statistically significant.
Simple logistic regression
Logistic regression assumes that the outcome variable is binary (i.e., coded as 0 and 1). We have only one variable in the hsb2 data file that is coded 0 and 1, and that is female. We understand that female is a silly outcome variable (it would make more sense to use it as a predictor variable), but we can use female as the outcome variable to illustrate how the code for this command is structured and how to interpret the output. The first variable listed after the logistic (or logit) command is the outcome (or dependent) variable, and all of the rest of the variables are predictor (or independent) variables. You can use the logit command if you want to see the regression coefficients or the logistic command if you want to see the odds ratios. In our example, female will be the outcome variable, and read will be the predictor variable. As with OLS regression, the predictor variables must be either dichotomous or continuous; they cannot be categorical.
logistic female read
Logit estimates Number of obs = 200
LR chi2(1) = 0.56
Prob > chi2 = 0.4527
Log likelihood = -137.53641 Pseudo R2 = 0.0020
------------------------------------------------------------------------------
female | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .9896176 .0137732 -0.75 0.453 .9629875 1.016984
------------------------------------------------------------------------------
logit female read
Iteration 0: log likelihood = -137.81834
Iteration 1: log likelihood = -137.53642
Iteration 2: log likelihood = -137.53641
Logit estimates Number of obs = 200
LR chi2(1) = 0.56
Prob > chi2 = 0.4527
Log likelihood = -137.53641 Pseudo R2 = 0.0020
------------------------------------------------------------------------------
female | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | -.0104367 .0139177 -0.75 0.453 -.0377148 .0168415
_cons | .7260875 .7419612 0.98 0.328 -.7281297 2.180305
------------------------------------------------------------------------------
The results indicate that reading score (read) is not a statistically significant predictor of gender (i.e., being female), z = -0.75, p = 0.453. Likewise, the test of the overall model is not statistically significant, LR chi-squared 0.56, p = 0.4527.
See also
- Stata Textbook Examples: Applied Logistic Regression (2nd Ed) Chapter 1
- Stata Web Books: Logistic Regression in Stata
- Stata Data Analysis Example: Logistic Regression
- Annotated Stata Output: Logistic Regression Analysis
- Stata FAQ: How do I interpret odds ratios in logistic regression?
- Stata Library
- Teaching Tools: Graph Logistic Regression Curve
Multiple regression
Multiple regression is very similar to simple regression, except that in multiple regression you have more than one predictor variable in the equation. For example, using the hsb2 data file we will predict writing score from gender (female), reading, math, science and social studies (socst) scores.
regress write female read math science socst
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 5, 194) = 58.60
Model | 10756.9244 5 2151.38488 Prob > F = 0.0000
Residual | 7121.9506 194 36.7110855 R-squared = 0.6017
-------------+------------------------------ Adj R-squared = 0.5914
Total | 17878.875 199 89.843593 Root MSE = 6.059
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | 5.492502 .8754227 6.27 0.000 3.765935 7.21907
read | .1254123 .0649598 1.93 0.055 -.0027059 .2535304
math | .2380748 .0671266 3.55 0.000 .1056832 .3704665
science | .2419382 .0606997 3.99 0.000 .1222221 .3616542
socst | .2292644 .0528361 4.34 0.000 .1250575 .3334713
_cons | 6.138759 2.808423 2.19 0.030 .599798 11.67772
------------------------------------------------------------------------------
The results indicate that the overall model is statistically significant (F = 58.60, p = 0.0000). Furthermore, all of the predictor variables are statistically significant except for read.
See also
- Regression with Stata: Lesson 1 – Simple and Multiple Regression
- Annotated Output: Multiple Linear Regression
- Stata Annotated Output: Regression
- Stata Teaching Tools
- Stata Textbook Examples: Applied Linear Statistical Models
- Stata Textbook Examples: Regression Analysis by Example, Chapter 3
Analysis of covariance
Analysis of covariance is like ANOVA, except in addition to the categorical predictors you also have continuous predictors as well. For example, the one way ANOVA example used write as the dependent variable and prog as the independent variable. Let’s add read as a continuous variable to this model, as shown below.
anova write prog c.read
Number of obs = 200 R-squared = 0.3925
Root MSE = 7.44408 Adj R-squared = 0.3832
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 7017.68123 3 2339.22708 42.21 0.0000
|
prog | 650.259965 2 325.129983 5.87 0.0034
read | 3841.98338 1 3841.98338 69.33 0.0000
|
Residual | 10861.1938 196 55.4142539
----------+----------------------------------------------------
Total | 17878.875 199 89.843593
The results indicate that even after adjusting for reading score (read), writing scores still significantly differ by program type (prog) F = 5.87, p = 0.0034.
See also
Multiple logistic regression
Multiple logistic regression is like simple logistic regression, except that there are two or more predictors. The predictors can be interval variables or dummy variables, but cannot be categorical variables. If you have categorical predictors, they should be coded into one or more dummy variables. We have only one variable in our data set that is coded 0 and 1, and that is female. We understand that female is a silly outcome variable (it would make more sense to use it as a predictor variable), but we can use female as the outcome variable to illustrate how the code for this command is structured and how to interpret the output. The first variable listed after the logistic (or logit) command is the outcome (or dependent) variable, and all of the rest of the variables are predictor (or independent) variables. You can use the logit command if you want to see the regression coefficients or the logistic command if you want to see the odds ratios. In our example, female will be the outcome variable, and read and write will be the predictor variables.
logistic female read write
Logit estimates Number of obs = 200
LR chi2(2) = 27.82
Prob > chi2 = 0.0000
Log likelihood = -123.90902 Pseudo R2 = 0.1009
------------------------------------------------------------------------------
female | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read | .9314488 .0182578 -3.62 0.000 .8963428 .9679298
write | 1.112231 .0246282 4.80 0.000 1.064993 1.161564
------------------------------------------------------------------------------
These results show that both read and write are significant predictors of female.
See also
- Stata Annotated Output: Logistic Regression
- Stata Library
- Stata Web Books: Logistic Regression with Stata
- Stata Textbook Examples: Applied Logistic Regression, Chapter 2
- Stata Textbook Examples: Applied Regression Analysis, Chapter 8
- Stata Textbook Examples: Introduction to Categorical Analysis, Chapter 5
- Stata Textbook Examples: Regression Analysis by Example, Chapter 12
Discriminant analysis
Discriminant analysis is used when you have one or more normally distributed interval independent variables and a categorical dependent variable. It is a multivariate technique that considers the latent dimensions in the independent variables for predicting group membership in the categorical dependent variable. For example, using the hsb2 data file, say we wish to use read, write and math scores to predict the type of program a student belongs to (prog). For this analysis, you need to first download the daoneway program that performs this test. You can download daoneway from within Stata by typing search daoneway (see How can I used the search command to search for programs and get additional help? for more information about using search).
You can then perform the discriminant function analysis like this.
daoneway read write math, by(prog)
One-way Disciminant Function Analysis
Observations = 200
Variables = 3
Groups = 3
Pct of Cum Canonical After Wilks'
Fcn Eigenvalue Variance Pct Corr Fcn Lambda Chi-square df P-value
| 0 0.73398 60.619 6 0.0000
1 0.3563 98.74 98.74 0.5125 | 1 0.99548 0.888 2 0.6414
2 0.0045 1.26 100.00 0.0672 |
Unstandardized canonical discriminant function coefficients
func1 func2
read 0.0292 -0.0439
write 0.0383 0.1370
math 0.0703 -0.0793
_cons -7.2509 -0.7635
Standardized canonical discriminant function coefficients
func1 func2
read 0.2729 -0.4098
write 0.3311 1.1834
math 0.5816 -0.6557
Canonical discriminant structure matrix
func1 func2
read 0.7785 -0.1841
write 0.7753 0.6303
math 0.9129 -0.2725
Group means on canonical discriminant functions
func1 func2
prog-1 -0.3120 0.1190
prog-2 0.5359 -0.0197
prog-3 -0.8445 -0.0658
Clearly, the Stata output for this procedure is lengthy, and it is beyond the scope of this page to explain all of it. However, the main point is that two canonical variables are identified by the analysis, the first of which seems to be more related to program type than the second.
See also
One-way MANOVA
MANOVA (multivariate analysis of variance) is like ANOVA, except that there are two or more dependent variables. In a one-way MANOVA, there is one categorical independent variable and two or more dependent variables. For example, using the hsb2 data file, say we wish to examine the differences in read, write and math broken down by program type (prog). For this analysis, you can use the manova command and then perform the analysis like this.
manova read write math = prog, category(prog)
Number of obs = 200
W = Wilks' lambda L = Lawley-Hotelling trace
P = Pillai's trace R = Roy's largest root
Source | Statistic df F(df1, df2) = F Prob>F
-----------+--------------------------------------------------
prog | W 0.7340 2 6.0 390.0 10.87 0.0000 e
| P 0.2672 6.0 392.0 10.08 0.0000 a
| L 0.3608 6.0 388.0 11.67 0.0000 a
| R 0.3563 3.0 196.0 23.28 0.0000 u
|--------------------------------------------------
Residual | 197
-----------+--------------------------------------------------
Total | 199
--------------------------------------------------------------
e = exact, a = approximate, u = upper bound on F
This command produces three different test statistics that are used to evaluate the statistical significance of the relationship between the independent variable and the outcome variables. According to all three criteria, the students in the different programs differ in their joint distribution of read, write and math. See also
- Stata Data Analysis Examples: One-way MANOVA
- Stata Annotated Output: One-way MANOVA
- Stata FAQ: How can I do multivariate repeated measures in Stata?
Multivariate multiple regression
Multivariate multiple regression is used when you have two or more dependent variables that are to be predicted from two or more predictor variables. In our example, we will predict write and read from female, math, science and social studies (socst) scores.
mvreg write read = female math science socst
Equation Obs Parms RMSE "R-sq" F P
----------------------------------------------------------------------
write 200 5 6.101191 0.5940 71.32457 0.0000
read 200 5 6.679383 0.5841 68.4741 0.0000
------------------------------------------------------------------------------
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
write |
female | 5.428215 .8808853 6.16 0.000 3.69093 7.165501
math | .2801611 .0639308 4.38 0.000 .1540766 .4062456
science | .2786543 .0580452 4.80 0.000 .1641773 .3931313
socst | .2681117 .049195 5.45 0.000 .1710892 .3651343
_cons | 6.568924 2.819079 2.33 0.021 1.009124 12.12872
-------------+----------------------------------------------------------------
read |
female | -.512606 .9643644 -0.53 0.596 -2.414529 1.389317
math | .3355829 .0699893 4.79 0.000 .1975497 .4736161
science | .2927632 .063546 4.61 0.000 .1674376 .4180889
socst | .3097572 .0538571 5.75 0.000 .2035401 .4159744
_cons | 3.430005 3.086236 1.11 0.268 -2.656682 9.516691
------------------------------------------------------------------------------
Many researchers familiar with traditional multivariate analysis may not recognize the tests above. They do not see Wilks’ Lambda, Pillai’s Trace or the Hotelling-Lawley Trace statistics, the statistics with which they are familiar. It is possible to obtain these statistics using the mvtest command written by David E. Moore of the University of Cincinnati. UCLA updated this command to work with Stata 6 and above. You can download mvtest from within Stata by typing search mvtest (see How can I used the search command to search for programs and get additional help? for more information about using search).
Now that we have downloaded it, we can use the command shown below.
mvtest female
MULTIVARIATE TESTS OF SIGNIFICANCE
Multivariate Test Criteria and Exact F Statistics for
the Hypothesis of no Overall "female" Effect(s)
S=1 M=0 N=96
Test Value F Num DF Den DF Pr > F
Wilks' Lambda 0.83011470 19.8513 2 194.0000 0.0000
Pillai's Trace 0.16988530 19.8513 2 194.0000 0.0000
Hotelling-Lawley Trace 0.20465280 19.8513 2 194.0000 0.0000
These results show that female has a significant relationship with the joint distribution of write and read. The mvtest command could then be repeated for each of the other predictor variables.
See also
- Regression with Stata: Chapter 4, Beyond OLS
- Stata Data Analysis Examples: Multivariate Multiple Regression
- Stata Textbook Examples, Econometric Analysis, Chapter 16
Canonical correlation
Canonical correlation is a multivariate technique used to examine the relationship between two groups of variables. For each set of variables, it creates latent variables and looks at the relationships among the latent variables. It assumes that all variables in the model are interval and normally distributed. Stata requires that each of the two groups of variables be enclosed in parentheses. There need not be an equal number of variables in the two groups.
canon (read write) (math science)
Linear combinations for canonical correlation 1 Number of obs = 200
------------------------------------------------------------------------------
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
u |
read | .0632613 .007111 8.90 0.000 .0492386 .077284
write | .0492492 .007692 6.40 0.000 .0340809 .0644174
-------------+----------------------------------------------------------------
v |
math | .0669827 .0080473 8.32 0.000 .0511138 .0828515
science | .0482406 .0076145 6.34 0.000 .0332252 .0632561
------------------------------------------------------------------------------
(Std. Errors estimated conditionally)
Canonical correlations:
0.7728 0.0235
The output above shows the linear combinations corresponding to the first canonical correlation. At the bottom of the output are the two canonical correlations. These results indicate that the first canonical correlation is .7728. You will note that Stata is brief and may not provide you with all of the information that you may want. Several programs have been developed to provide more information regarding the analysis. You can download this family of programs by typing search cancor (see How can I used the search command to search for programs and get additional help? for more information about using search).
Because the output from the cancor command is lengthy, we will use the cantest command to obtain the eigenvalues, F-tests and associated p-values that we want. Note that you do not have to specify a model with either the cancor or the cantest commands if they are issued after the canon command.
cantest
Canon Can Corr Likelihood Approx
Corr Squared Ratio F df1 df2 Pr > F
7728 .59728 0.4025 56.4706 4 392.000 0.0000
0235 .00055 0.9994 0.1087 1 197.000 0.7420
Eigenvalue Proportion Cumulative
1.4831 0.9996 0.9996
0.0006 0.0004 1.0000
The F-test in this output tests the hypothesis that the first canonical correlation is equal to zero. Clearly, F = 56.4706 is statistically significant. However, the second canonical correlation of .0235 is not statistically significantly different from zero (F = 0.1087, p = 0.7420).
See also
- Stata Data Analysis Examples: Canonical Correlation Analysis
- Stata Annotated Output: Canonical Correlation Analysis
- Stata Textbook Examples: Computer-Aided Multivariate Analysis, Chapter 10
Factor analysis
Factor analysis is a form of exploratory multivariate analysis that is used to either reduce the number of variables in a model or to detect relationships among variables. All variables involved in the factor analysis need to be continuous and are assumed to be normally distributed. The goal of the analysis is to try to identify factors which underlie the variables. There may be fewer factors than variables, but there may not be more factors than variables. For our example, let’s suppose that we think that there are some common factors underlying the various test scores. We will first use the principal components method of extraction (by using the pc option) and then the principal components factor method of extraction (by using the pcf option). This parallels the output produced by SAS and SPSS.
factor read write math science socst, pc
(obs=200)
(principal components; 5 components retained)
Component Eigenvalue Difference Proportion Cumulative
------------------------------------------------------------------
1 3.38082 2.82344 0.6762 0.6762
2 0.55738 0.15059 0.1115 0.7876
3 0.40679 0.05062 0.0814 0.8690
4 0.35617 0.05733 0.0712 0.9402
5 0.29884 . 0.0598 1.0000
Eigenvectors
Variable | 1 2 3 4 5
-------------+------------------------------------------------------
read | 0.46642 -0.02728 -0.53127 -0.02058 -0.70642
write | 0.44839 0.20755 0.80642 0.05575 -0.32007
math | 0.45878 -0.26090 -0.00060 -0.78004 0.33615
science | 0.43558 -0.61089 -0.00695 0.58948 0.29924
socst | 0.42567 0.71758 -0.25958 0.20132 0.44269
Now let’s rerun the factor analysis with a principal component factors extraction method and retain factors with eigenvalues of .5 or greater. Then we will use a varimax rotation on the solution.
factor read write math science socst, pcf mineigen(.5)
(obs=200)
(principal component factors; 2 factors retained)
Factor Eigenvalue Difference Proportion Cumulative
------------------------------------------------------------------
1 3.38082 2.82344 0.6762 0.6762
2 0.55738 0.15059 0.1115 0.7876
3 0.40679 0.05062 0.0814 0.8690
4 0.35617 0.05733 0.0712 0.9402
5 0.29884 . 0.0598 1.0000
Factor Loadings
Variable | 1 2 Uniqueness
-------------+--------------------------------
read | 0.85760 -0.02037 0.26410
write | 0.82445 0.15495 0.29627
math | 0.84355 -0.19478 0.25048
science | 0.80091 -0.45608 0.15054
socst | 0.78268 0.53573 0.10041
rotate, varimax
(varimax rotation)
Rotated Factor Loadings
Variable | 1 2 Uniqueness
-------------+--------------------------------
read | 0.64808 0.56204 0.26410
write | 0.50558 0.66942 0.29627
math | 0.75506 0.42357 0.25048
science | 0.89934 0.20159 0.15054
socst | 0.21844 0.92297 0.10041
Note that by default, Stata will retain all factors with positive eigenvalues; hence the use of the mineigen option or the factors(#) option. The factors(#) option does not specify the number of solutions to retain, but rather the largest number of solutions to retain. From the table of factor loadings, we can see that all five of the test scores load onto the first factor, while all five tend to load not so heavily on the second factor. Uniqueness (which is the opposite of commonality) is the proportion of variance of the variable (i.e., read) that is not accounted for by all of the factors taken together, and a very high uniqueness can indicate that a variable may not belong with any of the factors. Factor loadings are often rotated in an attempt to make them more interpretable. Stata performs both varimax and promax rotations.
rotate, varimax
(varimax rotation)
Rotated Factor Loadings
Variable | 1 2 Uniqueness
-------------+--------------------------------
read | 0.62238 0.51992 0.34233
write | 0.53933 0.54228 0.41505
math | 0.65110 0.45408 0.36988
science | 0.64835 0.37324 0.44033
socst | 0.44265 0.58091 0.46660
The purpose of rotating the factors is to get the variables to load either very high or very low on each factor. In this example, because all of the variables loaded onto factor 1 and not on factor 2, the rotation did not aid in the interpretation. Instead, it made the results even more difficult to interpret.
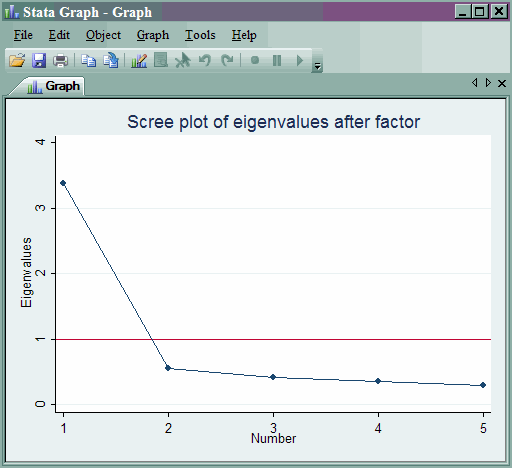
To obtain a scree plot of the eigenvalues, you can use the greigen command. We have included a reference line on the y-axis at one to aid in determining how many factors should be retained.
greigen, yline(1)